全栈工程师开发手册 （作者：栾鹏）

python数据挖掘系列教程

在了解线性函数前，先来了解一下线性回归和逻辑回归的区别。线性回归为估值而生，逻辑回归而分类而生。比如我们根据根据一家企业的运营质量、盈利、运营时间等来对企业进行估值，这属于估值问题，如果存在线性关系，属于线性回归问题。再比如我们对验证码图片进行识别，将图片通过线性函数也产生了一列值，但是我们的目的是为了识别图片中究竟是数字0、1、2、3、4、5、6、7、8、9中的几，所以我们还需要将线性函数产生的这一列值进行非线性变换，变换之后的结果能用来让我们分类。这是分类问题，是逻辑回归问题。

在今后的文章中，数据的组成形式存在两种可能。
1、样本数据集，每列代表一个对象。也就是说一个待测对象是一个列向量
2、样本数据集，每行代表一个对象。也就是说待测对象是一个行向量

线性函数

我们先在数学上理解线性函数。

在线性模型中，当我们想把待测对象x向量转化为数值结果y向量的时候，我们会推导出一个函数 Y=WX+B。这个就是线性函数。其中x为输入对象，x1、x2、x3为对象的特征属性，y是输出结果，y1、y2是结果的分量。权重W确定x在预测每个y的分量时的影响。而输出结果有几个分量这样看场景的目的。比如验证码，我如果想要每张验证码具体的值，值输出结果是1维的，如果想要输出验证码图片属于每个数字的概率，则验证码是10维的。

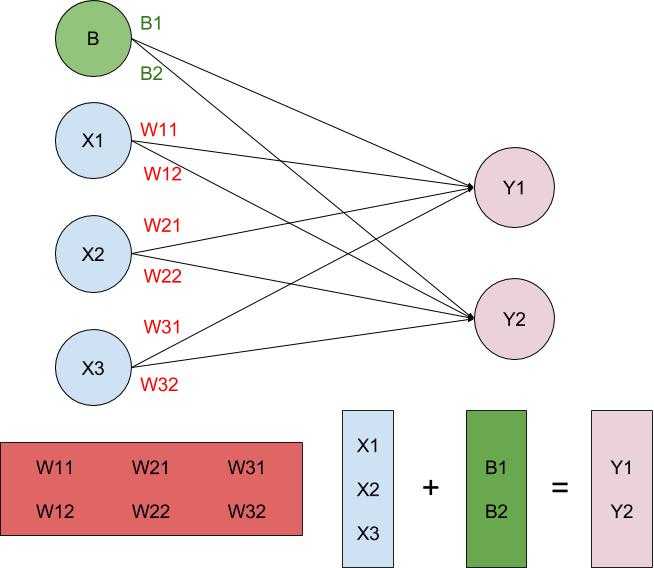
1、在很多线性回归模型中根本看不到B的存在，而仅写成Y=WX，从上图中也可以看出，这是因为B可以看成是输入对象一个值为1的属性所对应的权重。即y1=W11*X1+W21*X2+W31*X3+1*B1，这里Y的每个分量由输入对象每个属性线性组合得出。

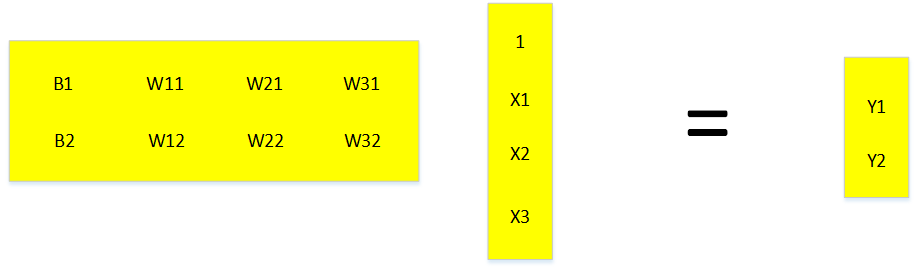
2、我们可以这样理解线性函数，权重w的某一行表示输入对象每个属性对输出分量的贡献率。比如w11表示待测样本属性x1对分量y1的贡献率，w21表示待测样本属性x2对分量y1的贡献率，w12表示待测样本属性x1对分量y2的贡献率。如果我们不需要预测Y2分量，权重矩阵就不存在W12，W22，W32。我们所以如果我们想要预测的结果不需要那么多分量，只是减少了权重矩阵的维度。

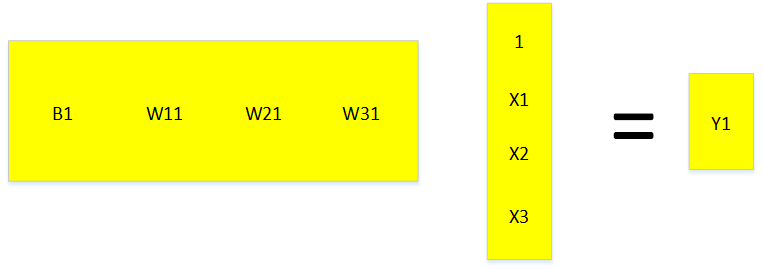
3、对于线性二分类，就是找到一个直接或平面超平面将两个集合分割开。
因此我们可以通过判断g(x)>0或g(x)<0进行判别。则分割面或分割线满足WX=0。所以他还是一个线性问题。

---

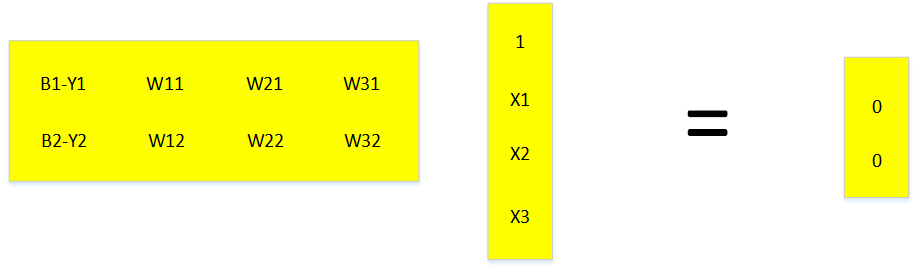
在线性函数的相关教程中比较容易混淆的就是行向量和列向量。有时你也会看到如下的写法。你会看到Y=WX和Y=XW等不同的写法，但是表达的思想是相同的 。

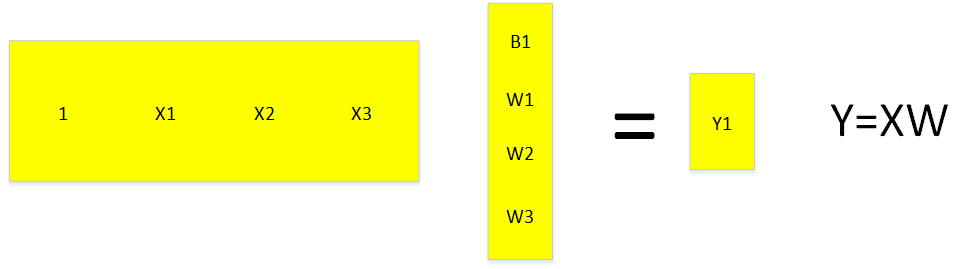
如论哪种写法，其中的x始终为一个输入对象，各分量为该对象的特征属性。只不过有些地方是以行向量的形式存在，有时是以列向量的形式存在。X是多个对象形成的样本数据集，只不过有时对象按列存在，有时按行存在。

当使用Y=WX时，X每列为一个对象，Y的每行为该对象的输出结果。当使用Y=XW时，X的每行为一个对象，Y的每列为该对象的输出结果。
甚至有时你会看到$Y=W^{T}X$或者$Y=W{X}^T$等各种形式的形式。

为什么看到的教程中输出结果y都是一个值，而不是向量？

我们知道输出一个值的结果时，y是对象每个属性的线性组合。当输出结果为向量y时，y的每个分量，是对象每个属性的线性组合。而对象属性组合成y 的每个分量时的权重系数是相互独立的。所以在输出结果为向量时，也就是先求出组合成y的第一个分量的系数，再求出第2个分量的组合系数。只是多做了几遍求解罢了。所以你看教程中看到的基本都是输出单个值y的情况。

当输出结果y为向量时，是使用矩阵同时对多组系数进行求解，而不是使用向量一个分量一个分量的求解。

线性回归

对于一个的拥有m个对象，n个属性的样本数据集而言，线性回归的目的就是建立一个线性函数。能对待测对象x，预测其对应的一个或者多个输出结果。

比如输入对象为一个富二代，属性为年龄、零花钱、运动时间，预测结果为身高，预测结果也可以为身高、体重。

而在我们平时看到的教程中，基本以预测一维数据为主，因为对于二维结果，我们可以分两次预测一维结果来形成。

所以下面的教程我们就以预测一维结果为例继续讲解。

如果预测的结果为一维的，即Y为一个数值，则Y=WX，其中W为[b1，w11，w12，w13]的行向量，X为[1，x1，x2，x3]列向量，公式展开便可以写成如下线性组合的样式，这也就是最简单的线性回归模型。

$$y=b1\ast 1+w11\ast x1+w12\ast x2+w13\ast x3$$

注：此处的X在原来x的基础上，左边又加了一列，且全是1。以此来代表B向量

这个就是一个组合问题，已知一些数据，如何求里面的未知参数，给出一个最优解。

寻找最优回归系数就是一种优化问题，我们在之前讲过一种优化问题。
参考：http://blog.csdn.net/luanpeng825485697/article/details/78765923

在今后的逻辑回归，SVM和神经网络，都是优化问题，都是问了使损失函数最小的题解。

只不过在那篇文章中优化问题处理的自变量为离散值的情况，线性回归问题中的自变量取值是连续值。

在线性回归中的损失函数时误差平方和。后面我们会看到其他损失函数。

为什么求解权重W，是求使误差平方和最小的矩阵，而不是直接数学运算呢？

这是因为一个线性矩阵方程，直接求解，很可能无法直接求解。有唯一解的数据集，微乎其微。基本上不存在这样一个权重矩阵满足你搜集的所有样本对象的输入输出关系。

因此，需要退一步，将参数求解问题，转化为求最小误差问题，即求出一个权重矩阵，使得对样本数据集中的对象进行预测，预测的结果与真实结果之间的误差尽可能小。如果样本数据集中包含m个对象，每次预测只输出一个值，则会进行m次预测，会有m个预测结果，也就会有m个预测结果的误差。

---

上面的教程我们知道了线性回归的目的。那么反应在数学上是什么问题呢？

求一个最优权值矩阵，直观上，就是使用这个权值矩阵进行预测的结果误差最小。对于包含m个对象的样本数据集，每个对象预测产生一个数值，则样本数据集就会产生m个预测值，就会产生m个误差值。一般我们采用使m个误差值的平方和最小的权值矩阵为最优权值矩阵。

（若X每列为一个对象，w为行向量，则误差平方和为）

${\sum }_{i=1}^m(y_i-w{x}_i{)}^2$

（若X每行为一个对象，w为列向量，则误差平方和为）

${\sum }_{i=1}^m(y_i-x_{i}w{)}^2$

这个误差平方和，被称为损失函数或者错误函数或者成本函数，它用来描述线性函数不好的程度。

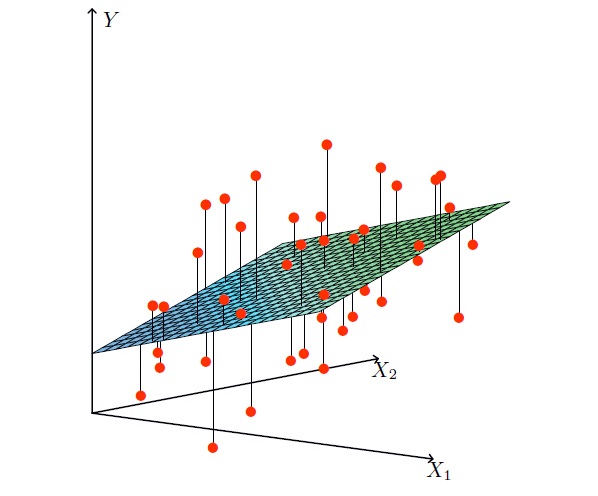
从下图来直观理解一下线性回归优化的目标——图中线段距离（平方）的平均值，也就是最小化到分割面的距离和。

线性回归中为什么一般选用误差平方和作为损失函数？

上面我教程中，我们使用误差平方和作为损失函数，用来评估模型预测结果，那么我们为啥一般选误差平方和作为损失函数呢？

假设模型结果与测量值 误差满足，均值为0的高斯分布，即正态分布。这个假设是靠谱的，符合一般客观统计规律。

数据x与y的条件概率：

$$p(y^{(i)}|x^{(i)};\theta )=\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})$$

若使 模型与测量数据最接近，那么其概率积就最大。概率积，就是概率密度函数的连续积，这样，就形成了一个最大似然函数估计敲打。对最大似然函数估计进行推导，就得出了求导后结果： 平方和最小公式。

也就是说选用误差平方和作为误差函数，其实就是将误差假定为了0均值的高斯正态分布。这也就是为什么还会存在sigmoid逻辑回归（以伯努利分布分析误差），以及softmax等一般线性回归（以指数分布分析误差）。

除了误差平方和还有哪些损失函数

线性回归中采用平方和的形式，一般都是由模型条件概率的最大似然函数 概率积最大值，求导，推导出来的。
统计学中，损失函数一般有以下几种：
1） 0-1损失函数

$ L(Y,f(X))= \begin{cases} 1, & \text {Y≠f(X)} \ 0, & \text{ Y=f(X)} \end{cases} $

2） 平方损失函数

$L(Y,f(X))=(Y-f(X){)}^2$

3） 绝对损失函数

$L(Y,f(X))=|Y-f(X)|$

4） 对数损失函数

$L(Y,P(Y|X))=-logP(Y|X)$

损失函数越小，模型就越好，而且损失函数 尽量 是一个凸函数，便于收敛计算。
线性回归，采用的是平方损失函数。而逻辑回归采用的是 对数 损失函数。

模型求解

接下来，我们就以误差平方和作为损失函数，以损失函数最小为目的来求解权重矩阵。有最小二乘法，梯度下降法、随机梯度下降法。

最小二乘法

我们的目的是求使损失函数最小的权重矩阵W。首先想到的就是数学中的求导。导数等于0的地方是极大值或极小值。最小二乘就是对损失函数求导，使导出等于0。（我们先暂且把他认为是最大值、最小值吧）

下面的公式还是以每个对象只预测一个数值结果为例。

有两种写法：

y=wx，其中w为横向量，x为列向量，y为数值。
y=xw，其中w为列向量，x为横向量，y为数值。

1、若用X表示多个样本对象，每行为一个对象。则要写成y=Xw，其中w为列向量，x为矩阵，y为列向量，每个分量表示每个对象的预测结果。此时误差平方和对权重矩阵w求导，为下面的公式。

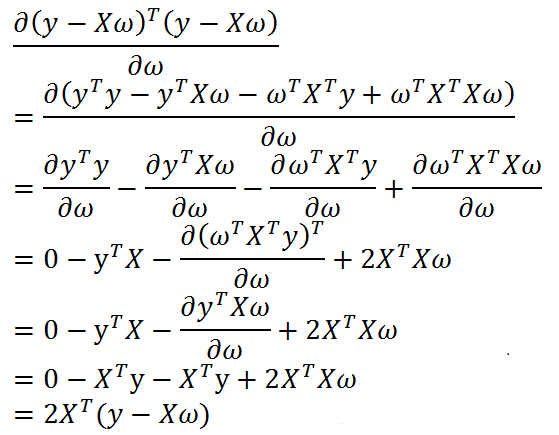
令上述公式等于0，得到：

$w=(X^{T}X{)}^{-1}{X}^{T}y$

这是当前可以估计出的w的最优解。从现有数据上估计出的w可能并不是数据中的真实w值，仅是w的一个最佳估计。

值得注意的是，上述公式中包含逆矩阵，也就是说，这个方程只在逆矩阵存在的时候使用，也即是这个矩阵是一个方阵，并且其行列式不为0。

也就是说最小二乘方法是一个直接的数学求解公式，不过它要求X是列满秩的。

2、若用X表示多个样本对象，每列为一个对象。则y=wX中，w为横向量，x为矩阵，y为横向量，每个分量表示每个对象的预测结果。此时误差平方和对权重矩阵w求导，为下面的公式。

$$\frac{d(y-wX{)}^T(y-wX)}{dw}$$

上式等于0，得到下面的公式。

$w=y^T{X}^T(X{X}^T{)}^{-1}$

梯度下降法

在梯度下降法和随机梯度下降法中，我们使用Y=XW的形式，是为了方便公式推导。X每行为一个样本对象。当每个对象仅预测一个值时，W为列向量。

分别有梯度下降法，批梯度下降法，增量梯度下降。本质上，都是偏导数，步长/最佳学习率，更新，收敛的问题。这个算法只是最优化原理中的一个普通的方法，可以结合最优化原理来学，就容易理解了。

所谓梯度也就是导数。只不过是多维空间下的导数。例如上面对权重矩阵w的求导就是w的梯度。
我们知道线性回归的损失函数为：（其中$x_i$为一个样本对象，行向量）

$J(w)={\sum }_{i=1}^m(x_{i}w-y_i{)}^2$

对w求导的导数为（X一行为一个对象，w为列向量）

$\frac{dJ(w)}{dw}=2X^T(Xw-y)$

上面这个导数就是w的梯度。

$\nabla J(w)=2X^T(Xw-y)$

而所谓的梯度更新，就是在原有形式上变化一个梯度的值。其中k表示第几次迭代，其中$\rho$是学习速率。

$w_{k+1}=w_k-\rho \ast \nabla J(w_k)=w_k-\rho \ast 2X^T(X{w}_k-y)$

画外音：还有一种算法叫做梯度上升法，就是将公式中的减号换成加号。

可以在下图中形象的理解梯度下降法。

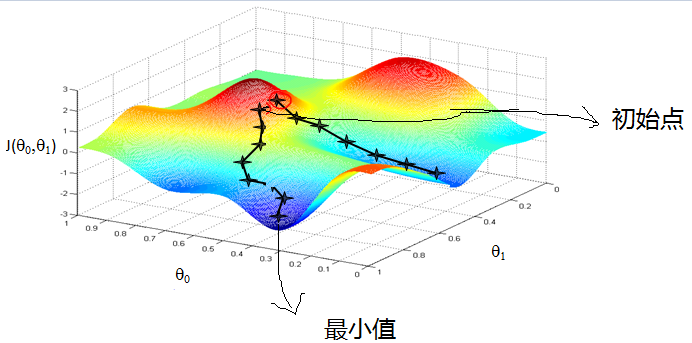
从上面的图可以看出：初始点不同，获得的最小值也不同，因此梯度下降求得的只是局部最小值；

注意：下降的步伐大小非常重要，因为如果太小，则找到函数最小值的速度就很慢，如果太大，则可能出现权值矩阵求解不再收敛；

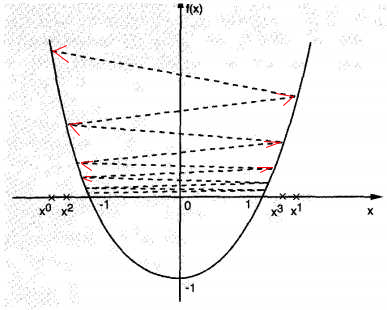
随机梯度下降法

随机梯度下降法，也称为在线学习算法，它不像上面的梯度下降法，每次迭代都使用了全部的数据集，这里每次迭代仅仅使用一个样本，这种方法在神经网络中使用的较多：（其中$x_k$为第k个样本对象，为行向量。$y_k$为该对象产生的预测输出数值。$w_k$为迭代第k次产生的权重列向量w，当对新的一行对象进行预测时，总是使用最新的w。${\rho }_k$ 为第k次迭代是使用的学习速度（也叫变化步长），每次迭代是使用的学习速度都不相同。刚开始学习速度快（步长大），越到后面，速度越慢（步长越短））

$w_{k+1}=w_k-2\ast {\rho }_k{x}_k^T(x_k{w}_k-y_k)$

这里需要说明的是，${\rho }_k$ 必须满足两个条件：

$\sum _{k=1}^{\infty }{\rho }_k\to \infty$

$\sum _{k=1}^{\infty }{\rho }_k^2<\infty$

这个过程，其实是根据新的输入样本，对$w$的一个不断的修正的过程，一般来说，我们会把${\rho }_k$ 后面的式子称为修正量。

折两个条件，保证了在迭代过程中估计的修正值，会趋近于零。因此，对于足够大的k而言，迭代会突然停止，但是，由于有第一个条件的存在，这个停止不会发生的太早，并且不会再离结果非常远的时候，就停止了迭代。上面的第二个条件保证了，对于变量的随机性噪声，噪声的累积保持有限。

去均值和归一化

此种方法应用于梯度下降，为了加快梯度下降的执行速度；
思想：将各个特征属性的值标准化，使得取值范围大致都在-1<=x<=1之间；

没有经过归一化，寻找最优解的过程：

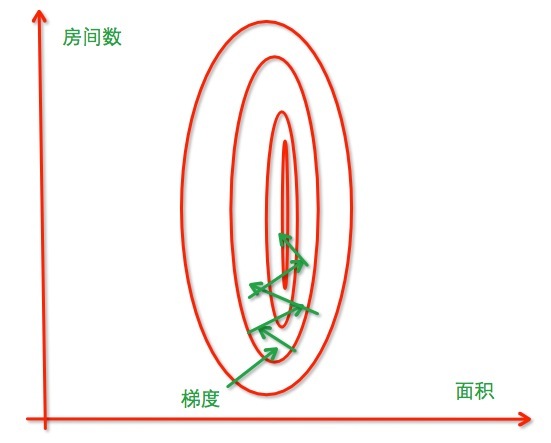
经过归一化，把各个特征的尺度控制在相同的范围内：

---

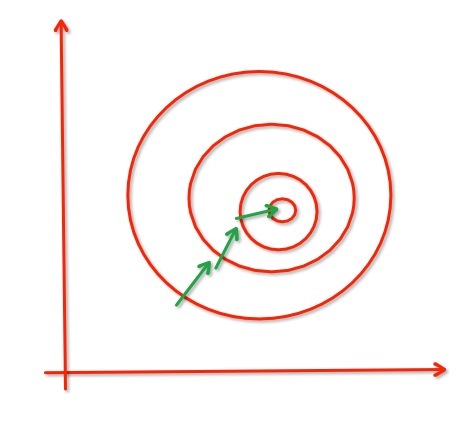
梯度下降和随机梯度下降的感想

通过误差不断调整权重主要有两个途径，一个是迭代次数，一个是样本数量。

以下图为例，假设只存在样本1和样本2，其中样本1会倾向于权重矩阵向左侧移动，样本2会倾向于权重矩阵向左侧移动。权重矩阵w的初始值在O1处，先使用样本1调整，w调整到O2处，再使用样本2调整，w调整到O3处。第一次迭代结束，开始进行第二次迭代，使用样本1调整，w调整到O4处，使用样本2调整，w调整到O5处，开始第三次迭代，使用样本1调整到O6处，使用样本2调整到O7处，结束。

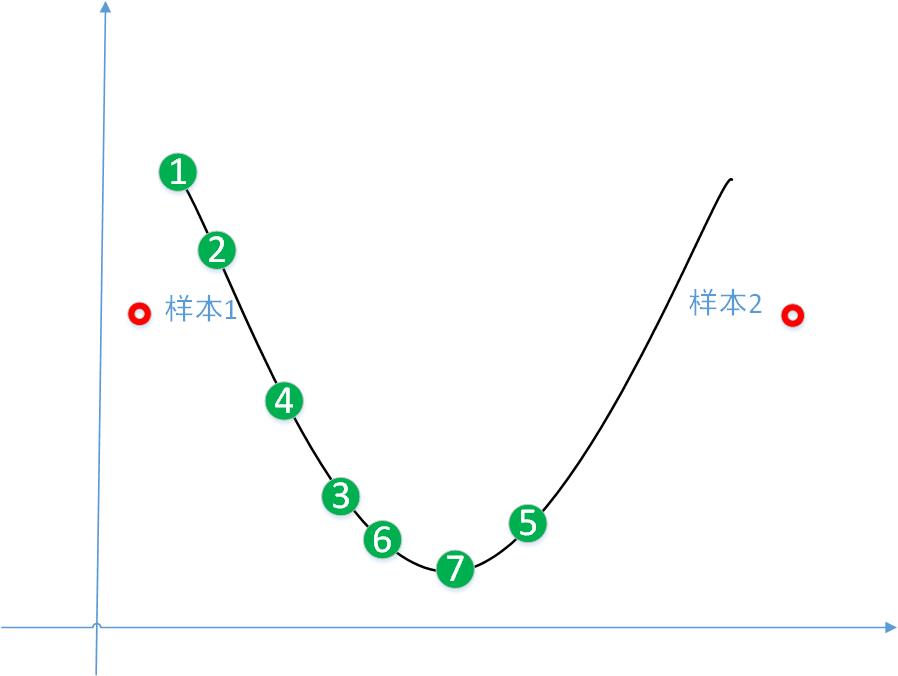
在这个过程我们理解到由于学习速率的存在同一个样本要迭代多次，才能充分发挥样本的作用，遍历每一个样本，才能充分利用每一个样本携带的信息。

---

线性回归案例

在学习线性回归以及今后的逻辑回归和神经网络必然用到库numpy，在numpy中存在array和matrix两种数据结构。

1. 当为array的时候，默认d*f就是对应元素的乘积，multiply也是对应元素的乘积，dot（d,f）会转化为矩阵的乘积， dot点乘意味着相加，而multiply只是对应元素相乘，不相加。

2. 当为mat的时候，默认d*f就是矩阵的乘积，multiply转化为对应元素的乘积，dot（d,f）为矩阵的乘积

一、单变量的线性回归

在本案例中，样本数据集每行为一个对象。对象属性只有一个x，对象预测值也只有一个y。

1、加载数据集

先构造一个简单的一维数据集，x和y近乎服从线性分布。第一列为第一个特征属性，即x数据，第二列为输出结果，即y数据（要预测的值）

0.067732	3.176513
0.427810	3.816464
0.995731	4.550095
0.738336	4.256571
0.981083	4.560815
0.526171	3.929515
0.378887	3.526170
0.033859	3.156393
0.132791	3.110301
0.138306	3.149813
0.247809	3.476346
0.648270	4.119688
0.731209	4.282233
0.236833	3.486582
0.969788	4.655492
0.607492	3.965162
0.358622	3.514900
0.147846	3.125947
0.637820	4.094115
0.230372	3.476039
0.070237	3.210610
0.067154	3.190612
0.925577	4.631504
0.717733	4.295890
0.015371	3.085028
0.335070	3.448080
0.040486	3.167440
0.212575	3.364266
0.617218	3.993482
0.541196	3.891471

我们知道使用y=xw进行计算时，其实是将偏量b算入了w中，为x添加了一个属性，值为1。因此在下面的数据集加载函数loadDataSet中，我们为样本数据第一列添加了一个值为1的属性。

import matplotlib.pyplot as plt
import numpy as np

#加载数据集，最后一列最为目标值，前面的为特征属性的值
def loadDataSet(fileName):
    xArr = []; yArr = []
    for line in open(fileName).readlines():
        curLine = line.strip().split('\t')
        xonerow = [1.0]   #添加1.0作为第一个系数，则第一个系数的权重用来代表y=wx+b中的b变量
        for i in range(len(curLine)-1):
            xonerow.append(float(curLine[i]))  #最后一列为输出结果值y，前面的值为输入x值
        xArr.append(xonerow)
        yArr.append(float(curLine[-1]))  #添加最后一列为结果值

    return xArr, yArr

使用可视化查看一下x-y的分布。

#绘制二维数据集
def plotDataSet():
    xArr, yArr = loadDataSet('data.txt')                                #加载数据集
    xcord = [xArr[i][1] for i in range(len(xArr))]
    ycord = [yArr[i] for i in range(len(yArr))]                         #样本点
    fig = plt.figure()
    ax = fig.add_subplot(111)                                            #添加subplot
    ax.scatter(xcord, ycord, s = 20, c = 'blue',alpha = .5)                #绘制样本点
    plt.xlabel('X');plt.ylabel('Y')
    plt.show()

if __name__ == '__main__':
    plotDataSet()

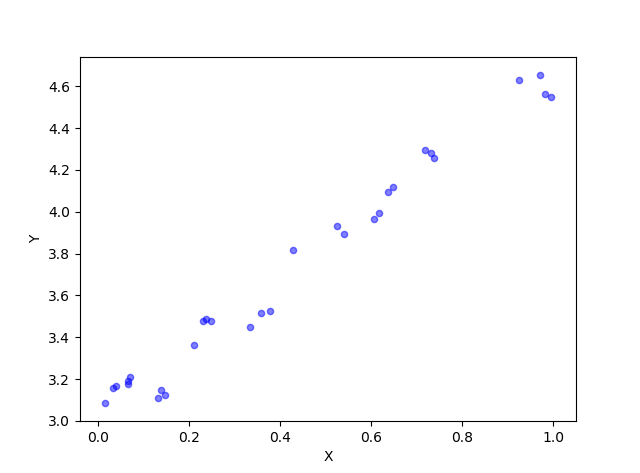
2、获取线性回归模型

最小二乘方法

我们知道使用下面的公式直接计算权重矩阵。

$w=(X^{T}X{)}^{-1}{X}^{T}y$

代码实现如下。

standRegres函数根据输入输出，计算回归系数w。

#最小二乘法计算回归系数。xArr为样本数据集，包含m个对象，n种属性。yarr为结果数据集
def standRegres(xArr,yArr):
    xMat = np.mat(xArr)       #转化为x矩阵。自动形成m行n列
    yMat = np.mat(yArr).reshape(len(yArr),1)     #转化为y列向量
    xTx = xMat.T * xMat       #根据文中推导的公示计算回归系数
    if np.linalg.det(xTx) == 0.0:   #对不能求逆的结果返回
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xMat.T*yMat)  #最小二乘求导出为0时的权重向量
    return ws

我们来调用一下这个函数，来试试求解w。

plotRegression函数先求解了回归系数w，然后绘制样本数据集点，又绘制了w系数（所谓绘制w就是绘制w所代表的直线）

# 绘制样本数据集，求解回归曲线，绘制回归曲线。regression为计算回归系数的函数
def plotRegression(regression):
    # 计算回归系数
    xArr, yArr = loadDataSet('data.txt')                                    #加载数据集
    ws = regression(xArr, yArr)                                           #计算回归系数列向量
    print(ws)

    xMat = np.mat(xArr)                                                    #创建xMat矩阵
    yMat = np.mat(yArr)                                                    #创建yMat矩阵（行向量）

    # 绘制样本数据集
    xarr = xMat[:, 1].flatten().A[0]  # 将矩阵第一列转化为一行矩阵，并获取第一行的列表
    yarr = yMat.flatten().A[0]  # 将矩阵第一列转化为一行矩阵，并获取第一行的行向量
    plt.scatter(xarr, yarr, s=20, c='blue', alpha=.5)  # 绘制样本点

    # 绘制回归系数。通过两个待测点，预测其值。以直线的形式反映出回归系数。
    testArr = np.array([[1,0],[1,1]])                                        #将对象[1,0]和对象[1,1]最为待测对象，第一个1为常值代表偏量，后面的分量代表属性x的值
    yHat = np.dot(testArr,ws)                                                      #计算使用线性模型预测的y值。dot就是矩阵乘法。
    plt.plot(testArr[:,1], yHat, c = 'red')                                #绘制回归曲线，x为第1列，y为结果列向量，
    plt.xlabel('X');plt.ylabel('Y')
    plt.show()

if __name__ == '__main__':
    plotRegression(standRegres)

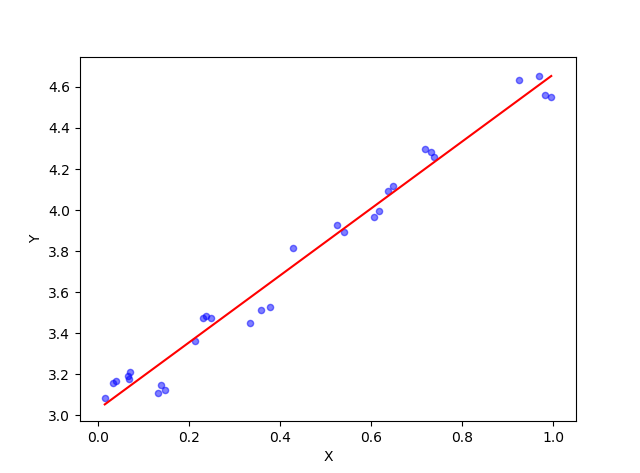
输出结果为
[[ 3.02863046]
[ 1.6314263 ]]

即线性模型为y=3.02+1.63*x

图中的直线就是w的图形表示。也就是y=3.02+1.63*x这条直线。

梯度下降法

根据上面的公式w的梯度为

$\nabla J(w)=2X^T(Xw-y)$

梯度下降法的更新公式为

$w_{k+1}=w_k-\rho \nabla J(w_k)$

用python实现上面的公式

#梯度下降法计算回归系数。xArr为属性数据集，每行为一个对象。yArr为结果数据集，每行为一个对象的结果。
def gradAscent(xArr,yArr):
    xMatrix = np.mat(xArr)                                        #转换成numpy的矩阵。xMatrix每行为一个对象，每列为一种特征属性
    yMatrix = np.mat(yArr).reshape(len(yArr),1)            #转换成numpy的矩阵,并变维成列向量
    m, n = np.shape(xMatrix)                                            #返回dataMatrix的大小。m为样本对象的个数,n为列数。
    alpha = 0.001                                                        #移动步长,也就是学习速率,控制更新的幅度。
    maxCycles = 500                                                      #最大迭代次数
    weights = np.ones((n,1))                                             #初始化权重列向量
    for k in range(maxCycles):
        h =  xMatrix * weights                               #梯度上升矢量化公式，计算预测值（列向量）
        error = h - yMatrix                                            #计算误差
        weights = weights - alpha * 2 * xMatrix.T * error                 # 调整回归系数
    return weights.getA()                                                #将矩阵转换为数组，返回权重数组

我们来调用一下上面的梯度下降法，试试求解回归系数w。

仍然使用上面的plotRegression函数

if __name__ == '__main__':
    plotRegression(gradAscent)

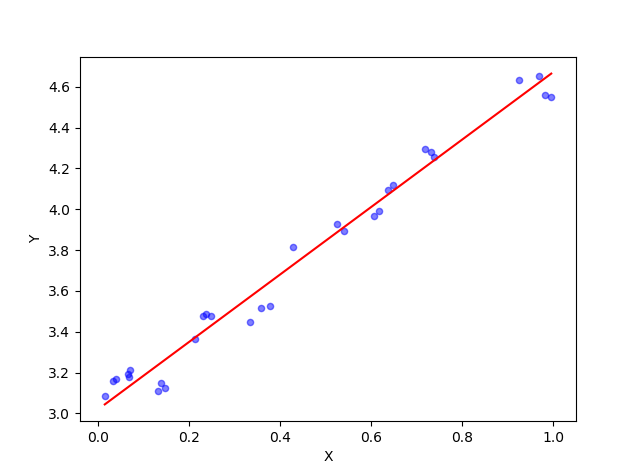
输出结果为
[[ 3.01830318]
[ 1.65370732]]

即线性模型为y=3.02+1.65*x

结果与使用最小二乘法获得的线性模型基本一致。

随机梯度下降法求解回归系数

根据前面理论部分的推导我们知道随机梯度下降法

$w_{k+1}=w_k-2\ast {\rho }_k{x}_k^T(x_k{w}_k-y_k)$

（其中$x_k$为第k个样本对象，为行向量。$y_k$为该对象产生的预测输出数值。$w_k$为迭代第k次产生的权重列向量w，当对新的一行对象进行预测时，总是使用最新的w。）

其中学习速率${\rho }_k$要满足，具体取什么值呢，其实并没有规定。

$\sum _{k=1}^{\infty }{\rho }_k\to \infty$

$\sum _{k=1}^{\infty }{\rho }_k^2<\infty$

学习速率大，会不收敛，学习速率小会收敛慢，所以这是个尝试的过程。

在随机梯度中，我们使用如下的形式。i为第几次迭代，k为迭代到第几行数据了。

$ \rho_k =\frac{4}{(1.0 + i + k)} + 0.01$

实现代码

#随机梯度下降法计算回归系数
def randgradAscent(xArr,yArr):
    xMatrix = np.mat(xArr)                                        #转换成numpy的矩阵。xMatrix每行为一个对象，每列为一种特征属性
    yMatrix = np.mat(yArr).reshape(len(yArr),1)                   #转换成numpy的矩阵,并变维成列向量
    m, n = np.shape(xMatrix)                                            #返回dataMatrix的大小。m为样本对象的个数,n为列数。
    maxCycles = 100                                                      #最大迭代次数
    weights = np.ones((n,1))                                             #初始化权重列向量
    for i in range(maxCycles):
        for k in range(m):
            alpha = 4 / (1.0 + i + k) + 0.01                       # 降低alpha的大小，每次减小1/(j+i)。刚开始的时候可以步长大一点，后面调整越精细
            h =  xMatrix[k] * weights                                      #随机梯度上升矢量化公式，计算预测值y
            error = h - yMatrix[k]                                            #计算误差
            weights = weights - 2*alpha * xMatrix[k].T * error                 # 调整回归系数
    return weights.getA()                                                #将矩阵转换为数组，返回权重数组

同样进行计算绘制

if __name__ == '__main__':
    plotRegression(randgradAscent)

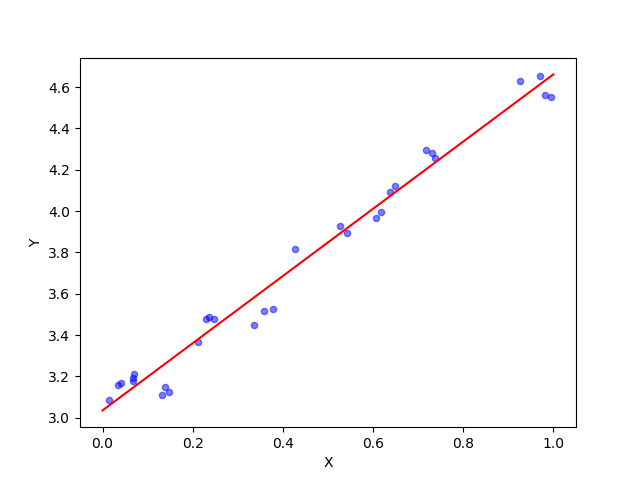
得到的结果为

[[ 3.03501804]
[ 1.62654039]]

即线性模型为y=3.03+1.62*x

结果与使用最小二乘法获得的线性模型基本一致。

---

拟合：拟合模型/函数

在学习后面的内容前，我们先来了解一下拟合问题。

一个模型在训练数据上能够获得比其他模型更好的拟合， 但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个模型出现了过拟合的现象。出现这种现象的主要原因是训练数据中存在噪音或者训练数据太少。

例如下图

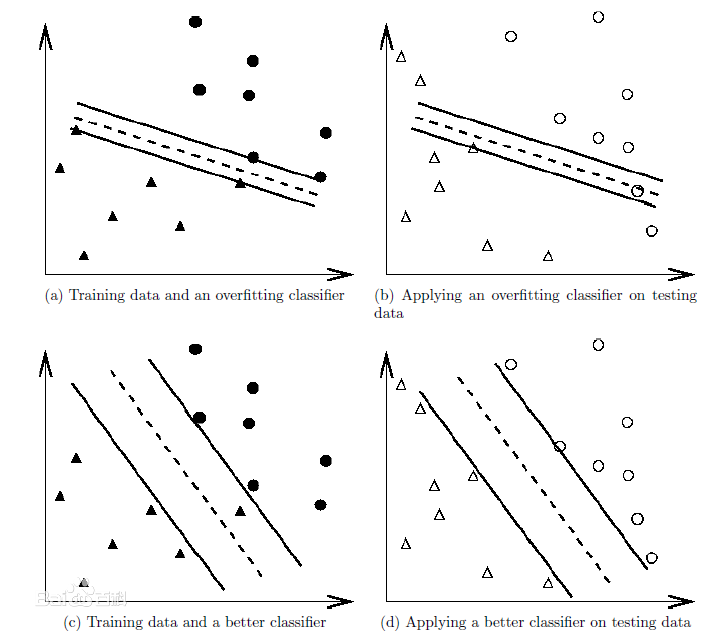
可以看出当样本数较少时，如图中a所以，我们建立的分类模型会如a中所示，虽然完全的拟合了样本数据，但是当数据集增大时，如b图中所示，测试数据分类准确度很差。这就是过拟合现象。

正确的建模应该如c中所示，虽然没有完全拟合样本数据，但在对于测试数据的分类准确度却很高，如图d。

过拟合问题往往是由于训练数据少、样本噪声等原因造成的。

根据样本数据，建立模型。根据拟合的模型是否合适？可分为以下三类：

1、合适拟合
2、欠拟合，或者叫作叫做高偏差(bias)。
3、过拟合，也叫高方差(variance)。

再用几个简单的图形象了解一下过拟合和欠拟合。

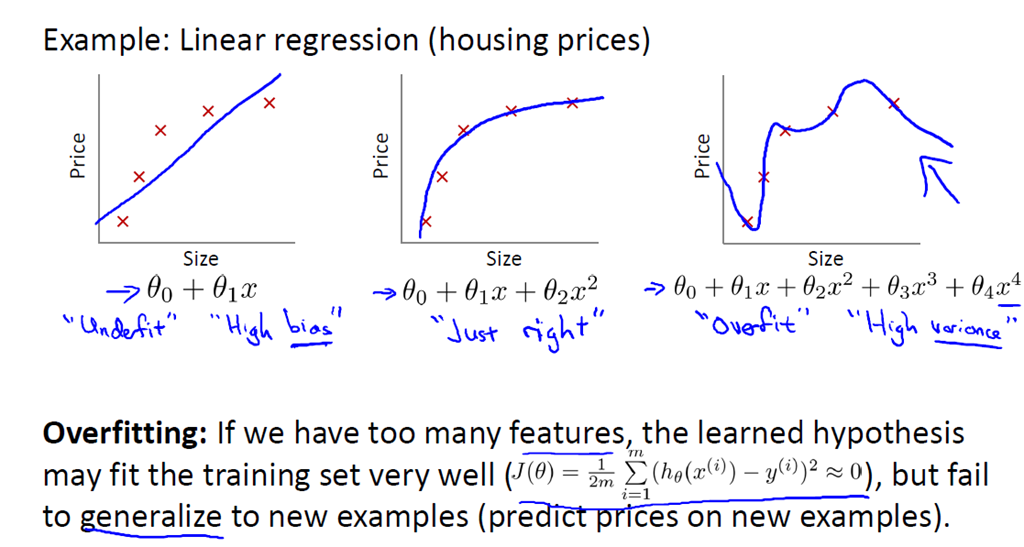
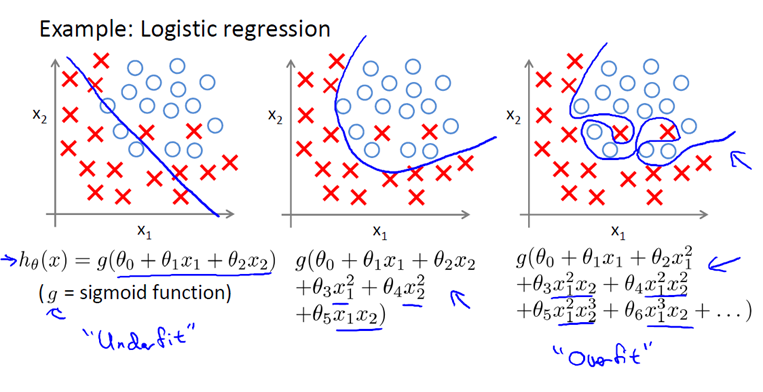
在线性回归中就可能会出现过拟合和欠拟合的问题。下面我们就来解决这两种问题。

正则化（处理过拟合）：

过拟合的问题如何解决？

问题起源？模型太复杂，参数过多，特征数目过多。

方法：

1） 减少特征的数量，有人工选择，或者采用模型选择算法
http://www.cnblogs.com/heaad/archive/2011/01/02/1924088.html （特征选择算法的综述）

2） 正则化，即保留所有特征，但降低参数的值的影响。正则化的优点是，特征很多时，每个特征都会有一个合适的影响因子。

拟合问题的状况，在线性回归问题中就是损失函数的量值不同。

正则化就是为防止过度拟合的模型出现（过于复杂的模型），在损失函数里增加一个每个特征的惩罚因子。如正则化的线性回归的损失函数：

$$J(w)=\frac{1}{2m}[\sum _{i=1}^m(h_w(x^{(i)})-y^{(i)}{)}^2]+\lambda \sum _{j=1}^n{w}_j^2$$

$\lambda$就是惩罚因子。
正则化是模型处理的典型方法。也是结构风险最小的策略。在经验风险（误差平方和）的基础上，增加一个惩罚项/正则化项。

则最小二乘线性回归的解，也转化为

$$w=(X^{T}X+\lambda \left(\begin{array}{ccccc}0& & & & \\ & 1& & & \\ & & 1& & \\ & & & \cdots & \\ & & & & 1\end{array}\right){)}^{-1}{X}^{T}y$$

括号内的矩阵，即使在样本数小于特征数的情况下，也是可逆的。

逻辑回归的正则化：

$$J(w)=-[\frac{1}{m}\sum _{i=1}^m{y}^{(i)}log{h}_w(x^{(i)})+(1-y^{(i)})log(1-h_w(x^{(i)}))]+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$$

从贝叶斯估计来看，正则化项对应模型的先验概率，复杂模型有较大先验概率，简单模型具有较小先验概率。这个里面又有几个概念。

L1正则化、L2正则化

L1正则化和L2正则化可以看做是损失函数的惩罚项。对于线性回归模型，使用L1正则化的模型建叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）。

L1正则化是指权值向量w中各个元素的绝对值之和，通常表示为$||w|{|}_1$

$$J(w)=\frac{1}{2m}[\sum _{i=1}^m(h_w(x^{(i)})-y^{(i)}{)}^2+\lambda \sum _{j=1}^n|w_j|]$$

L2正则化是指权值向量w中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为$||w|{|}_2$

$$J(w)=\frac{1}{2m}[\sum _{i=1}^m(h_w(x^{(i)})-y^{(i)}{)}^2]+\lambda \sum _{j=1}^n{w}_j^2$$

L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择。这是因为w绝对值求和这个正则项求导产生的后果是：当w为正时，更新后的w变小。当w为负时，更新后的w变大。因此它的效果就是让w往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。

但是由于lasso回归的损失函数是不可导的，所以梯度下降算法将不再有效，下面利用坐标轴下降法进行求解。

坐标轴下降法和梯度下降法具有同样的思想，都是沿着某个方向不断迭代，但是梯度下降法是沿着当前点的负梯度方向进行参数更新，而坐标轴下降法是沿着坐标轴的方向。

L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合

L2 和 L1 采用不同的方式降低权重：

• L2 会降低权重2。
• L1 会降低 |权重|。

因此，L2 和 L1 具有不同的导数：

• L2 的导数为 2 * 权重。
• L1 的导数为 k（一个常数，其值与权重无关）。

可以将 L2 的导数的作用理解为每次移除权重的 x%。如 Zeno 所知，对于任意数字，即使按每次减去 x% 的幅度执行数十亿次减法计算，最后得出的值也绝不会正好为 0。（Zeno 不太熟悉浮点精度限制，它可能会使结果正好为 0。）总而言之，L2 通常不会使权重变为 0。

可以将 L1 的导数的作用理解为每次从权重中减去一个常数。不过，由于减去的是绝对值，L1 在 0 处具有不连续性，这会导致与 0 相交的减法结果变为 0。例如，如果减法使权重从 +0.1 变为 -0.2，L1 便会将权重设为 0。就这样，L1 使权重变为 0 了。

L1 正则化 - 减少所有权重的绝对值 - 证明对宽度模型非常有效。

总结就是：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。

坐标轴下降法（解决L1正则化不可导的问题）

设lasso回归的损失函数为：

$$J(w)=\frac{1}{2m}[\sum _{i=1}^m(h_w(x^{(i)})-y^{(i)}{)}^2+\lambda \sum _{j=1}^n|w_j|]$$

其中，m为样本个数，n为特征个数。

由于lasso回归的损失函数是不可导的，所以梯度下降算法将不再有效，下面利用坐标轴下降法进行求解。

坐标轴下降法和梯度下降法具有同样的思想，都是沿着某个方向不断迭代，但是梯度下降法是沿着当前点的负梯度方向进行参数更新，而坐标轴下降法是沿着坐标轴的方向。

梯度下降法：优化目标在w的n个坐标轴上(或者说向量的方向上)对损失函数做迭代的下降，当所有的坐标轴上的$w_i$(i = 1,2,…n)都达到收敛时，我们的损失函数最小，此时的w即为我们要求的结果。

坐标轴下降法进行参数更新时，每次总是固定另外n-1个值，求另外一个的局部最优值，这样也避免了Lasso回归的损失函数不可导的问题。

坐标轴下降法每轮迭代都需要O(mn)的计算。（和梯度下降算法相同）

坐标轴下降法的数学依据为：对于一个可微凸函数，其中为的向量，如果对于一个解，使得在某个坐标轴上都能达到最小值，则就是的全局的最小值点。

局部加权线性回归（处理欠拟合）

线性回归的另一个问题是有可能出现欠拟合现象，因为它求的是具有小均方误差的无偏估 计。显而易见，如果模型欠拟合将不能取得好的预测效果。所以有些方法允许在估计中引入一 些偏差，从而降低预测的均方误差。

其中的一个方法是局部加权线性回归（LWLR）。在该方法中，我们给待预测点附近的每个点赋予一定的权重。与KNN一样，这种算法每次预测均需要事先计算样本对象与待测对象的距离，并根据距离为样本对象中的对象赋予权值。

注意：这个算法中涉及两个W矩阵，一个是根据待测对象为每个样本对象设置的权值矩阵W。它是一个对角矩阵，维度和样本数据集的对象个数相等。每个对角上的值，表示每个样本对象的权值。另外一个矩阵W就是我们要求得的回归系数矩阵W。

该算法解出回归系数W的形式如下：公式中的大写W为权重矩阵，小写w为回归系数。

$$w=(X^{T}WX{)}^{-1}{X}^{T}Wy$$

这个公式跟我们上面推导的公式的区别就在于权重矩阵W，它用来给每个点赋予权重。不同的待测对象的权重矩阵是不同的。

LWLR使用”核”（与支持向量机中的核类似）来对附近的点赋予更高的权重。核的类型可以自由选择，最常用的核就是高斯核，高斯核对应的权重如下：其中$W(i,i)$表示权重矩阵第i个对角值，$x_i$表示第i个样本对象，$x$表示待测对象。

$$W(i,i)=exp(-\frac{(x_i-x{)}^2}{2k^2})$$

我们通过改变k的值，可以调节回归效果。

实现代码

import matplotlib.pyplot as plt
import numpy as np

#加载数据集，最后一列最为目标值，前面的为特征属性的值
def loadDataSet(fileName):
    xArr = []; yArr = []
    for line in open(fileName).readlines():
        curLine = line.strip().split('\t')
        xonerow = [1.0]   #添加1.0作为第一个系数，则第一个系数的权重用来代表y=wx+b中的b变量
        for i in range(len(curLine)-1):
            xonerow.append(float(curLine[i]))  #最后一列为输出结果值y，前面的值为输入x值
        xArr.append(xonerow)
        yArr.append(float(curLine[-1]))  #添加最后一列为结果值

    return xArr, yArr


# 局部加权线性回归。绘制多条局部加权回归曲线
def plotlwlrRegression():
    xArr, yArr = loadDataSet('data.txt')                                    #加载数据集
    xMat = np.mat(xArr)                                                    #创建xMat矩阵。属性数据集，每行为一个样本对象，每列为一种属性
    yMat = np.mat(yArr).reshape(len(yArr),1)                               #创建yMat矩阵。将结果值存储成列向量

    testMat = xMat                     #原样选取样本数据集作为测试集。看看预测结果与真实结果之间的差距
    m = np.shape(testMat)[0]          # 计算待测数据集的样本个数
    yHat_1 = []  # 定义一个列表用来存储预测值
    yHat_2 = []  # 定义一个列表用来存储预测值
    yHat_3 = []  # 定义一个列表用来存储预测值
    for i in range(m):  # 对每个待测样本点进行预测
        yHat_1.append(lwlr(testMat[i,:], xMat, yMat, 1.0))                    # 根据局部加权线性回归计算yHat
        yHat_2.append(lwlr(testMat[i,:], xMat, yMat, 0.01))                   # 根据局部加权线性回归计算yHat
        yHat_3.append(lwlr(testMat[i,:], xMat, yMat, 0.003))                   # 根据局部加权线性回归计算yHat
    yHat_1 = np.mat(yHat_1).reshape(len(yHat_1),1)
    yHat_2 = np.mat(yHat_2).reshape(len(yHat_2), 1)
    yHat_3 = np.mat(yHat_3).reshape(len(yHat_3), 1)


    srtInd = xMat[:, 1].argsort(0)                                              #将样本数据集，第2列排序，返回索引值
    xSort = xMat[srtInd][:,0,:]                                                 #根据排序索引，将所有列排序
    ySort_1 = yHat_1[srtInd][:,0,:]
    ySort_2 = yHat_2[srtInd][:,0,:]
    ySort_3 = yHat_3[srtInd][:,0,:]

    fig, axs = plt.subplots(nrows=3, ncols=1,figsize=(10,8))                    #创建三个子图
    axs[0].plot(xSort[:,1], ySort_1, c = 'red',marker='.')                        #绘制回归曲线
    axs[1].plot(xSort[:,1], ySort_2, c = 'red',marker='.')                        #绘制回归曲线
    axs[2].plot(xSort[:,1], ySort_3, c = 'red',marker='.')                        #绘制回归曲线

    axs[0].scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0], s = 20, c = 'blue', alpha = .5)                #绘制样本点
    axs[1].scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0], s = 20, c = 'blue', alpha = .5)                #绘制样本点
    axs[2].scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0], s = 20, c = 'blue', alpha = .5)                #绘制样本点

    #设置标题,x轴label,y轴label
    axs0_title_text = axs[0].set_title(u'k=1.0', size=8, weight='bold', color='red')
    axs1_title_text = axs[1].set_title(u'k=0.01', size=8, weight='bold', color='red')
    axs2_title_text = axs[2].set_title(u'k=0.003', size=8, weight='bold', color='red')


    plt.xlabel('X');plt.ylabel('Y')
    plt.show()


# 使用局部加权线性回归计算回归系数w。不同的待测点获得的回归系数都不同。testPoint待测对象，xArr样本数据集，yArr结果数据集，k - 高斯核的k，表示拟合程度，为0表示100%拟合,自定义参数
def lwlr(testPoint, xMat, yMat, k = 1.0):
    m = np.shape(xMat)[0]                                               # 获取样本数量
    weights = np.mat(np.eye((m)))                                       # 初始化局部权重对角矩阵。这里的局部权重矩阵是为待测点周边的每个节点赋予的影响矩阵。并不是线性回归系数。
    for j in range(m):                                                 # 遍历数据集计算每个样本的权重
        diffMat = testPoint - xMat[j,:]                                # 计算样本中每个对象与待测对象之间的距离
        weights[j, j] = np.exp(diffMat * diffMat.T/(-2.0 * k**2))       # 为每个周边节点设定权重。越近的节点权重越大，越远的节点权重越小
    xTx = xMat.T * (weights * xMat)                                     #  增加了局部权重矩阵，增大临近节点的影响力，降低远方节点的影响力
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xMat.T * (weights * yMat))                            # 计算回归系数
    y = testPoint * ws                                                  # 计算预测值，矩阵相乘得到的是矩阵。虽然只有一个元素
    return y[0,0]       #读取矩阵的值，返回数值


if __name__ == '__main__':
    plotlwlrRegression()

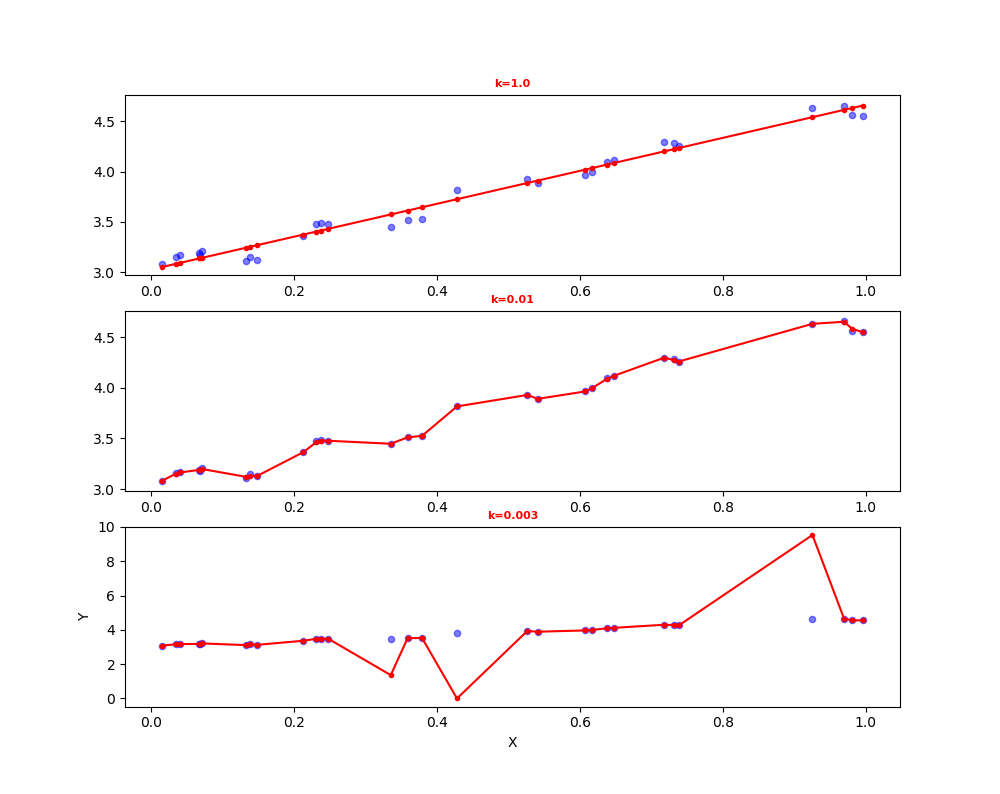
结果分析：很明显，当k=1.0时，回归曲线与散点图欠拟合(underfitting)，此时权重很大，如同将所有数据视为等权重，相当于普通线性回归模型；当k=0.01时得到了很好的效果；当k=0.003时，回归曲线与散点图过拟合(overfitting)，由于纳入了太多的噪声点，拟合的直线与数据点过于贴近，此时也不属于理想的模型。