深度学习的相关文章中一直提到两个词——梯度和梯度下降。在网上搜索这些词汇时，初学者常常会看到一堆公式和各种复杂的定义，可能会让人打退堂鼓。

然而，理解梯度的概念对于掌握深度学习至关重要。今天，我们将用一些通俗易懂的比喻来解释深度学习中的梯度。通过这种方式，希望能帮助大家更轻松地理解这个重要概念，从而更加自信地迈向深度学习的世界。

一、什么是梯度？

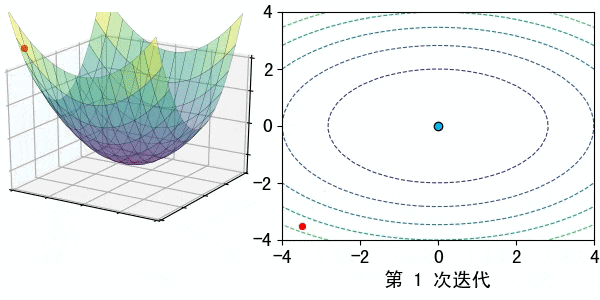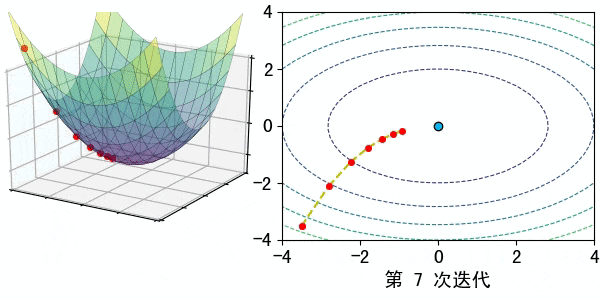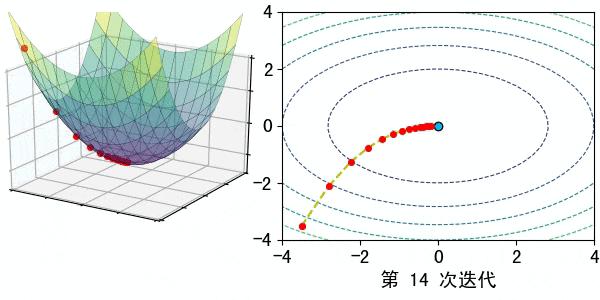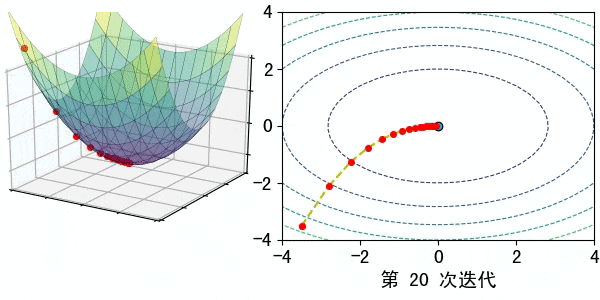
在深度学习中，梯度可以看作是一个指引我们如何调整模型参数（如权重和偏置）以最小化误差的指南针。梯度告诉我们，在当前参数值的情况下，误差朝哪个方向增大或减小，以及应该调整参数多少。

想象你在爬一座大山，你的目标是找到山的最低点（误差最小的地方）。你戴着眼罩，所以看不到周围的环境。你只能通过脚下的感觉来判断是否在下坡。

山顶：你现在所在的位置，误差比较大。

山谷：你要去的地方，误差最小。

梯度：地面的斜度和方向，告诉你应该朝哪个方向走，才能更快地到达山谷。

每次你感受到脚下的斜度（计算梯度），你就根据这个斜度调整方向，朝着下坡的方向走一步（更新模型参数）。不断重复这个过程，直到你感觉走到了最低点。

二、梯度计算

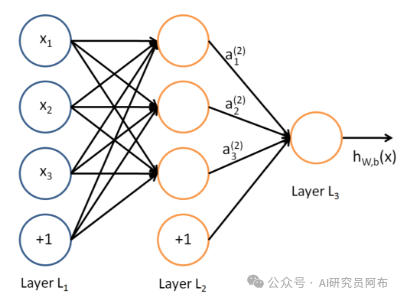
在深度学习中，我们通常使用反向传播算法来计算梯度。反向传播通过链式法则，从输出层开始，逐层向回计算每个参数对误差的影响。

数学解释

损失函数（Loss Function）：衡量模型预测与真实值之间的误差。例如，均方误差（MSE）。

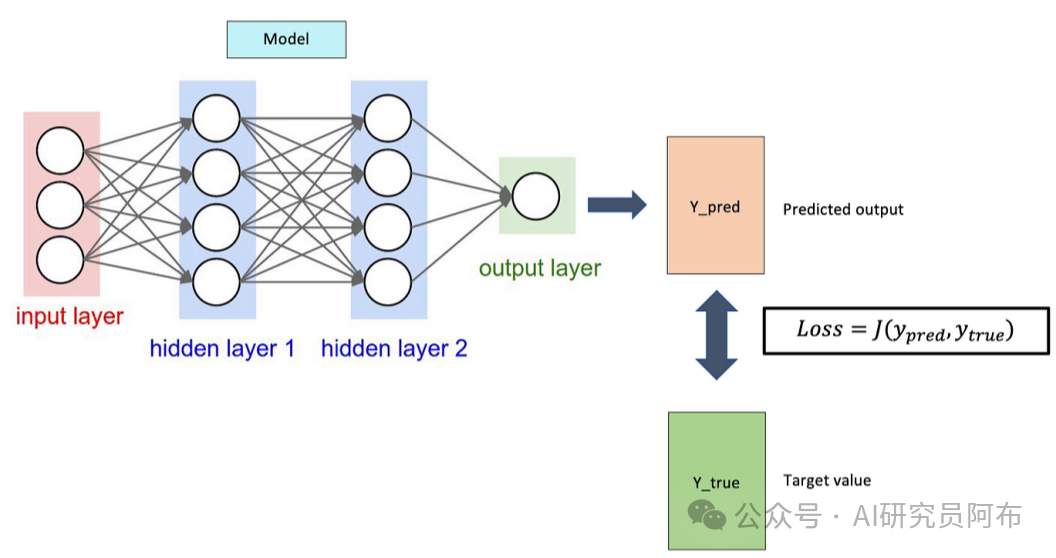
梯度（Gradient）：损失函数相对于模型参数的导数，表示误差随着参数变化的变化率。

三、优化算法

计算出梯度后，我们使用优化算法（如梯度下降）来更新模型参数。常见的优化算法有：

梯度下降（Gradient Descent）：沿着梯度的方向更新参数。

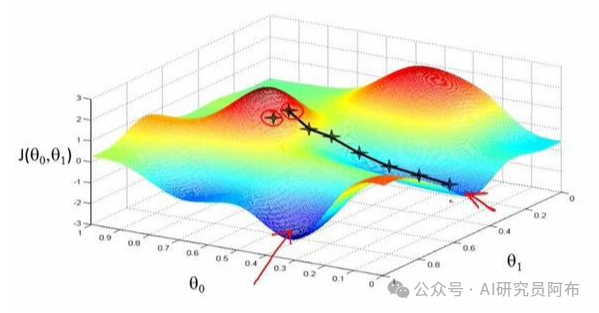
随机梯度下降（SGD）：每次使用一个或几个样本计算梯度进行更新。

自适应优化算法（如Adam、RMSprop）：根据梯度历史动态调整更新步长。

四、示例

假设我们有一个简单的线性模型，用来预测房价：

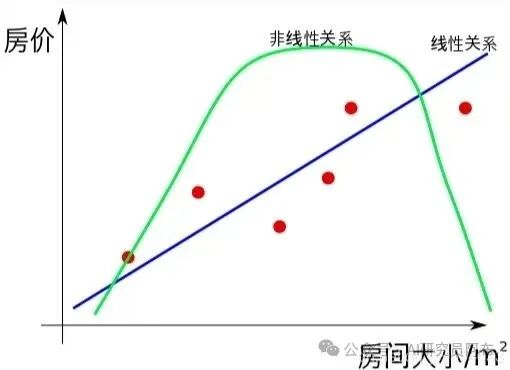
输入：房子的面积、房龄等特征。

模型参数：线性模型的权重和偏置。

损失函数：预测房价与真实房价之间的均方误差。

五、梯度的作用

初始化模型参数：随机初始化权重和偏置。

前向传播：计算模型预测值和损失。

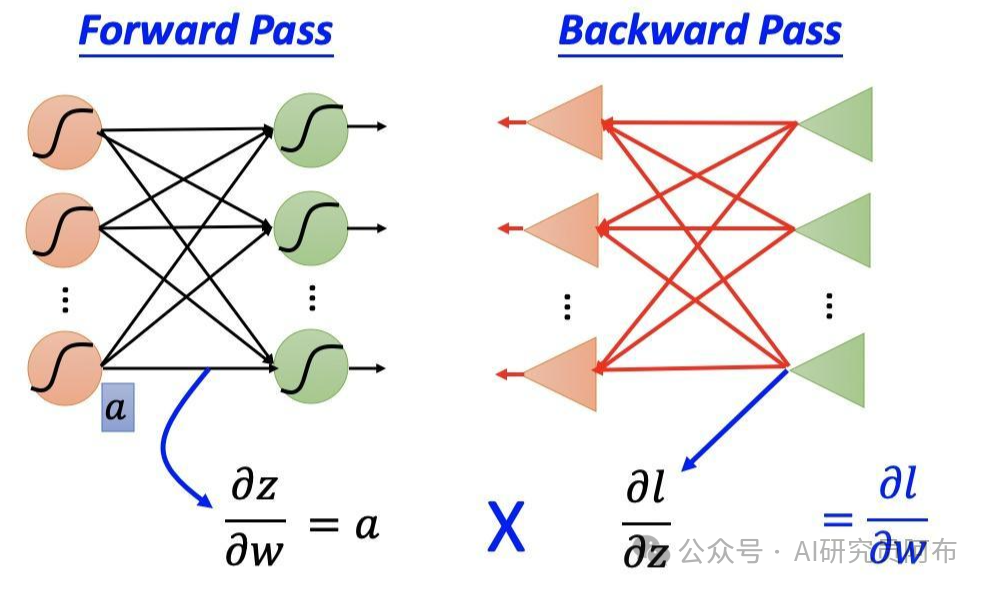
反向传播：计算损失函数相对于每个参数的梯度。

更新参数：根据梯度调整参数，使损失减小。

重复：不断进行前向传播、反向传播和参数更新，直到损失收敛。

六、形象化解释

当前参数：你站在山坡上。

损失函数：山的高度，代表误差。

梯度：脚下的斜度和方向，告诉你该往哪个方向走。

优化算法：你决定走多远，步子大小。

通过不断调整参数，你最终可以找到让模型误差最小的参数配置，这样你的模型就能够更准确地进行预测。

最后

选择AI大模型就是选择未来！最近两年，大家都可以看到AI的发展有多快，我国超10亿参数的大模型，在短短一年之内，已经超过了100个，现在还在不断的发掘中，时代在瞬息万变，我们又为何不给自己多一个选择，多一个出路，多一个可能呢？

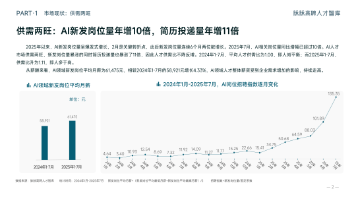
与其在传统行业里停滞不前，不如尝试一下新兴行业，而AI大模型恰恰是这两年的大风口，整体AI领域2025年预计缺口1000万人，人才需求急为紧迫！

由于文章篇幅有限，在这里我就不一一向大家展示了，学习AI大模型是一项系统工程，需要时间和持续的努力。但随着技术的发展和在线资源的丰富，零基础的小白也有很好的机会逐步学习和掌握。

【2025最新】AI大模型全套学习籽料（可白嫖）：LLM面试题+AI大模型学习路线+大模型PDF书籍+640套AI大模型报告等等，从入门到进阶再到精通，超全面存下吧！

获取方式：有需要的小伙伴，可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】
包括：AI大模型学习路线、LLM面试宝典、0基础教学视频、大模型PDF书籍/笔记、大模型实战案例合集、AI产品经理合集等等

大模型学习之路，道阻且长，但只要你坚持下去，一定会有收获。本学习路线图为你提供了学习大模型的全面指南，从入门到进阶，涵盖理论到应用。
L1阶段：启航篇|大语言模型的基础认知与核心原理

L2阶段：攻坚篇|高频场景:RAG认知与项目实践

L3阶段：跃迀篇|Agent智能体架构设计

L4阶段：精进篇|模型微调与私有化部署

L5阶段：专题篇|特训集：A2A与MCP综合应用 追踪行业热点（全新升级板块）

AI大模型全套学习资料【获取方式】