系列文章目录

机器学习——scikit-learn库学习、应用
机器学习——最小二乘法拟合曲线、正则化
机器学习——使用朴素贝叶斯分类器实现垃圾邮件检测（python代码+数据集）

---

---

线性回归

线性回归（Linear Regression）是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析，有一元线性回归和多元线性回归。在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。这些模型被叫做线性模型。最常用的线性回归建模是给定X值的y的条件均值是X的仿射函数。不太一般的情况，线性回归模型可以是一个中位数或一些其他的给定X的条件下y的条件分布的分位数作为X的线性函数表示。像所有形式的回归分析一样，线性回归也把焦点放在给定X值的y的条件概率分布，而不是X和y的联合概率分布（多元分析领域）。线性回归模型经常用最小二乘逼近来拟合，但他们也可能用别的方法来拟合，比如用最小化“拟合缺陷”在一些其他规范里（比如最小绝对误差回归），或者在桥回归中最小化最小二乘损失函数的惩罚。相反,最小二乘逼近可以用来拟合那些非线性的模型.因此，尽管“最小二乘法”和“线性模型”是紧密相连的，但他们是不能划等号的。

最小二乘法介绍

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小 。最小二乘法还可用于曲线拟合，其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达 。最小二乘法是解决曲线拟合问题最常用的方法。其基本思路是：令

其中，${\phi }_k(x)$是事先选定的一组线性无关的函数， ${\alpha }_k$是待定系数 ，拟合准则是使$y_i$与$f(x_i)$的距离 的平方和最小，称为最小二乘准则 。
基本原理

实验内容

代码

编译环境：python
下面代码主要使用了scipy库的最小二乘法求解函数leastsq 。
原理：最小误差平方和，已知多个近似分布于同一直线上的点，求解出一条直线，并使得所有点到直线上的距离平方和最小。满足这个条件的直线参数：斜率和截距，就是最小二乘法的解。因为函数封装好了，具体怎么写的的我也不知道。函数官网

import numpy as np
import scipy as sp
from scipy.optimize import leastsq
import matplotlib.pyplot as plt

# 1.目标函数,进行拟合的数据点都分布在这条正弦曲线附近
def real_func(x):   
    return np.sin(2*np.pi*x)  # y=sin⁡(2πx)函数

# 2.多项式  numpy.poly1d([1,2,3]) 生成1𝑥^2+2𝑥^1+3𝑥^0，p为多项式的参数,x为下面linspace(0, 1, 10)取得的点
def fit_func(p, x):
    f = np.poly1d(p) # 生成多项式 
    return f(x)

# 3.残差 误差函数，所谓误差就是指我们拟合的曲线的值减应真实值的差
def residuals_func(p, x, y):
    ret = fit_func(p, x) - y
    return ret

# 4.十个点
x = np.linspace(0, 1, 10) #linspace均分计算指令,产生在0-1之间的10个均等分值
x_points = np.linspace(0, 1, 1000)  # 产生在0-1之间的1000个均等分值
# 加上正态分布噪音的目标函数的值
y_ = real_func(x) # 在y=sin⁡(2πx)上得到与10个x点对应的y值
y = [np.random.normal(0, 0.1) + y1 for y1 in y_] # 10个y值分别加上均值为0标准差为0.1正态分布噪声


# 5.关于拟合的曲线的函数
def fitting(M=0):
    # M为多项式的次数，随机初始化多项式参数，生成M+1个随机数的列表，这样poyld函数返回的多项式次数就是M
    p_init = np.random.rand(M + 1)
    # 最小二乘法,三个参数：误差函数、函数参数列表，数据点
    p_lsq = leastsq(residuals_func, p_init, args=(x, y))  # 找到10个点对应误差和最小值所对应的参数
    print('Fitting Parameters:', p_lsq[0])

    # 可视化
    plt.plot(x_points, real_func(x_points), label='real')  # 真实曲线
    plt.plot(x_points, fit_func(p_lsq[0], x_points), label='fitted curve')  # 拟合曲线
    plt.plot(x, y, 'bo', label='noise')   # 噪声点
    plt.legend() #图例
    plt.show()
    return p_lsq

调用

# M为多项式的参数量
p_lsq_0= fitting(M=0)

运行结果

M=0, y=b
欠拟合
Fitting Parameters: [-0.02879864]

M=1, y=ax+b
欠拟合
Fitting Parameters: [-1.10093738 0.47688398]

M=3, $y=a{x}^3+b{x}^2+cx+d$
Fitting Parameters: [ 21.2488383 -31.70792373 10.68020074 -0.11486241]
结果最好

M=9, $y=a{x}^9+...+d$
Fitting Parameters: [-9.35004939e+03 4.52973025e+04 -9.27915993e+04 1.04312477e+05
-6.98022532e+04 2.81644008e+04 -6.57678844e+03 7.74517551e+02
-2.79125652e+01 -4.21686953e-02]
过拟合

造成过拟合的原因一个是权重矩阵W中的值太大了，一个是W中的值太多了即神经网络节点的个数太多了。解决办法就是要么将W值变小，要么将节点个数变少。这样做的后果就是使得神经网络更加接近线性，这样就会在过拟合和欠拟合之间取得一个合适的情况即适度拟合

正则化

正则化是用来防止模型过拟合而采取的手段，我们对代价函数增加一个限制条件，限制其较高次的参数大小不能过大。其中 λ称为正则化参数（Regularization Parameter），当参数越大，则对其惩罚（规范）的力度也就越大，越能起到规范的作用。但是要注意，λ并不是越大越好的！如果选择的正则化参数 太大，则会把所有的参数都最小化了，导致模型参数为0，造成欠拟合。因此，我们对 λ的选取需要合理即可。
L1正则化公式：$L=E(w)+\lambda \Vert w\Vert$
L2正则化公式：$L=E(w)+1/2\lambda w^2$
λ为惩罚参数，w为多项式参数,E(w)为初始误差。

L1正则化对于所有权重予以同样的惩罚，也就是说，不管模型参数的大小，对它们都施加同等力度的惩罚，因此，较小的权重在被惩罚后，就会变成0。因此，在经过L1正则化后，大量模型参数的值变为0或趋近于0，当然也有一部分参数的值飙得很高。由于大量模型参数变为0，这些参数就不会出现在最终的模型中，因此达到了稀疏化的作用，这也说明了L1正则化自带特征选择的功能，这一点十分有用。

L2正则化对于绝对值较大的权重予以很重的惩罚，对于绝对值很小的权重予以非常非常小的惩罚，当权重绝对值趋近于0时，基本不惩罚。这个性质与L2的平方项有关系，即越大的数，其平方越大，越小的数，比如小于1的数，其平方反而越小。

这里选择L2更为合适。

regularization = 0.0001

def residuals_func_regularization(p, x, y):
    ret = residuals_func(p, x, y)
    ret = np.append(ret, np.sqrt(0.5*regularization*np.square(p))) # L2范数作为正则化项
    return ret
# 最小二乘法,加正则化项
p_init = np.random.rand(9+1)
p_lsq_regularization = leastsq(residuals_func_regularization, p_init, args=(x, y))

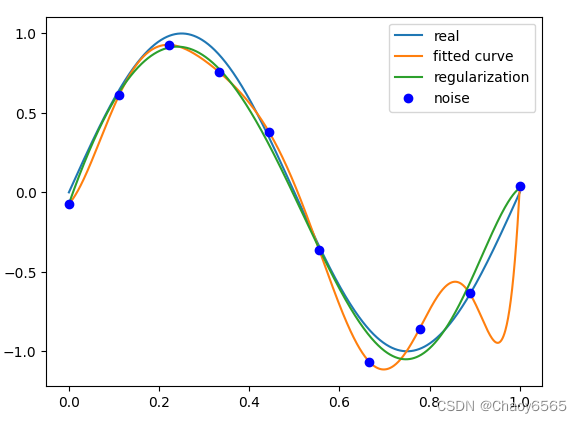
plt.plot(x_points, real_func(x_points), label='real')
plt.plot(x_points, fit_func(p_lsq_0[0], x_points), label='fitted curve')
plt.plot(x_points, fit_func(p_lsq_regularization[0], x_points), label='regularization')
plt.plot(x, y, 'bo', label='noise')
plt.legend()

正则化结果：

---

总结