题目链接：

https://download.csdn.net/download/ASUNAchan/86511275

1. 1）证明任何旋转矩阵的行列式的值恒为1

方法1：旋转矩阵 R 把n维空间中的一组标准正交基转化成另一组标准正交基，这两组标准正交基分别用矩阵 E E’来表示

即：
$$RE=E^{\prime }$$
因为
$$det(E)=1$$
所以
$$det(RE)=1$$

$$det(R)det(E)=1$$

所以
$$det(R)=1$$
方法2：

由旋转矩阵定义，可知，绕x轴旋转的旋转矩阵为：

同理可以得到Ry，Rz

对于Rx，Ry，Rz显然它的行列式为1

对于绕任意轴旋转的转转矩阵
$$M=Rz\ast Ry\ast Rx$$
又因为
$$det(AB)=det(A)det(B)$$
所以
$$det(M)=det(Rz\ast Ry\ast Rx)=det(Rz)det(Ry)det(Rx)=1$$

2. 3）编程求解齐次变换矩阵的逆矩阵

C++代码

#include <iostream>
#include <string.h>
using namespace std;

int main(int argc, char *argv[])
{
    //输入齐次变换矩阵---------------------------------
    double T[4][4];
    int icount, jcount;
    cout << "请输入齐次变换矩阵 T: " << endl;
    for (icount = 0; icount < 4; icount++)
    {
        for (jcount = 0; jcount < 4; jcount++)
        {
            cin >> T[icount][jcount];
        }
    }

    //得到旋转矩阵-------------------------------------
    double R[3][3];
    cout << "输出旋转矩阵 R: " << endl;
    for (icount = 0; icount < 3; icount++)
    {
        for (jcount = 0; jcount < 3; jcount++)
        {
            R[icount][jcount] = T[icount][jcount];
            cout << R[icount][jcount] << " ";
        }
        cout << endl;
    }

    //得到平移向量-------------------------------------
    double p[3];
    cout << "输出平移向量 p: " << endl;
    for (icount = 0; icount < 3; icount++)
    {
        p[icount] = T[icount][3];
        cout << p[icount] << " " << endl;
    }

    //求旋转矩阵的转置----------------------------------
    //求R的转置 行变列 列变行
    double R_T[icount][jcount];
    cout << "输出旋转矩阵的转置 R_T: " << endl;
    for (icount = 0; icount < 3; icount++)
    {
        for (jcount = 0; jcount < 3; jcount++)
        {
            R_T[icount][jcount] = R[jcount][icount];
            cout << R_T[icount][jcount] << " ";
        }
        cout << endl;
    }

    //旋转矩阵与平移向量相乘-----------------------------
    double p_mj[jcount];
    double p_mi[icount];
    cout << "旋转矩阵与向量相乘 p_mi: " << endl;
    for (icount = 0; icount < 3; icount++)
    {
        int t = 0;
        for (jcount = 0; jcount < 3; jcount++)
        {
            
            p_mj[jcount] = R_T[icount][jcount] * p[jcount];
            t = t + p_mj[jcount];
        }
        p_mi[icount] = t;
        cout << p_mi[icount] << " " << endl;
    }

    //变换矩阵T的逆 T_inverse---------------------------
    double T_inverse[4][4];
    for (icount = 0; icount < 4; icount++)
    {
        if (icount < 3)
        {
            for (jcount = 0; jcount < 4; jcount++)
            {
                if (jcount < 3)
                {
                    T_inverse[icount][jcount] = R_T[icount][jcount];
                }
                else
                {
                    T_inverse[icount][jcount] = -p_mi[icount];
                }
            }
            
        }
        else
        {
            for (jcount = 0; jcount < 4; jcount++)
            {
                if (jcount < 3)
                {
                    T_inverse[icount][jcount] = 0;
                }
                else
                {
                    T_inverse[icount][jcount] = 1;
                }
            }
        }
    }

    cout << "输出齐次变换矩阵的逆 T_inverse: " << endl;
    for (icount = 0; icount < 4; icount++)
    {
        for (jcount = 0; jcount < 4; jcount++)
        {
            cout << T_inverse[icount][jcount] << " ";
        }
        cout << endl;
    }

    return 0;
}

测试结果：

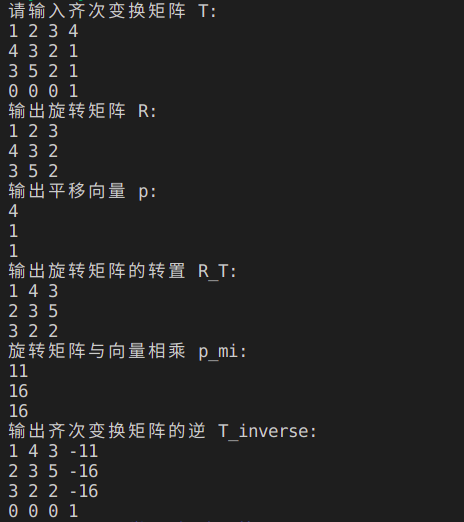
3.1）如图1所示三自由度机械臂，建立运动学正反解模型，并进行仿真验证。

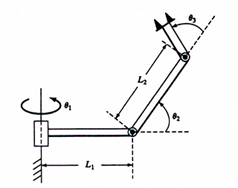
使用matlab所内置的机器人工具箱进行正逆运动学仿真实验。

步骤：

（1）根据已知结构写出此机械臂的D-H参数

i	alpha(i-1)	a(i-1)	d(i)	theta(i)
1	pi/2	l1	0	theta1
2	0	l2	0	theta2
3	0	l3	0	theta3

（2）将机械臂的各个参数以及D-H参数写入程序

​ 设l1 = 80，l2 = 60，l3 = 30

（3）调用正逆运动学函数进行仿真并绘制图像

逆运动学实现：

给定末端位置求关节角度

clear ; clc; close all;
% 机器人各连杆DH参数
d1 = 0;
d2 = 0;
d3 = 0;

a1 = 80;
a2 = 60;
a3 = 30;

alpha1 = 0.5 * pi;
alpha2 = 0 ;
alpha3 = 0;

% 定义各个连杆，默认为转动关节
%           theta      d        a        alpha 
L1=Link([  0         d1      a1      alpha1]); L(1).qlim=[-pi,pi];
L2=Link([  0         d2      a2      alpha2]); L(2).qlim=[-pi,pi]; L2.offset=pi/3;
L3=Link([  0         d3      a3      alpha3]); L(3).qlim=[-pi,pi]; L3.offset=-pi/3;

robot=SerialLink([L1 L2 L3],'name','robot');

T1=transl(80,0,90);%根据给定起始点，得到起始点位姿
T2=transl(140,0,-30 );%根据给定终止点，得到终止点位姿
q1=robot.ikine(T1,'mask', [1 1 1 0 0 0]);%根据起始点位姿，得到起始点关节角
q2=robot.ikine(T2,'mask', [1 1 1 0 0 0]);%根据终止点位姿，得到终止点关节角

[q ,qd, qdd]=jtraj(q1,q2,50); %五次多项式轨迹，得到关节角度，角速度，角加速度，50为采样点个数
T=robot.fkine(q);%根据插值，得到末端执行器位姿
T_t = transl(T);

figure
plot(T_t);
legend('x','y','z');

figure
plot(q);
legend('theta1','theta2','theta3');

nT=T.T; 
figure
plot3(squeeze(nT(1,4,:)),squeeze(nT(2,4,:)),squeeze(nT(3,4,:)));%输出末端轨迹
hold on
robot.plot(q);%动画演示

运行结果：

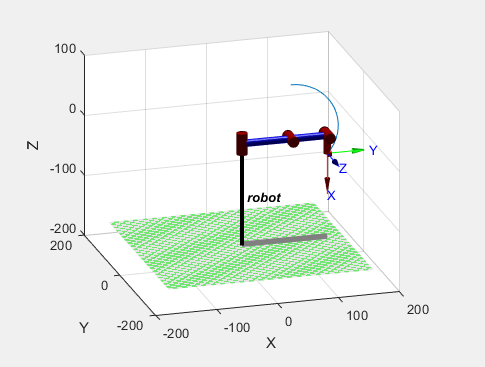
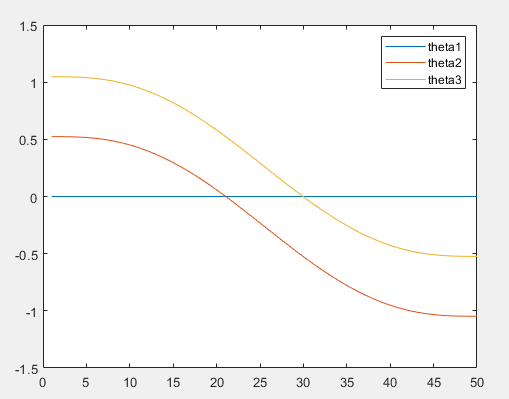
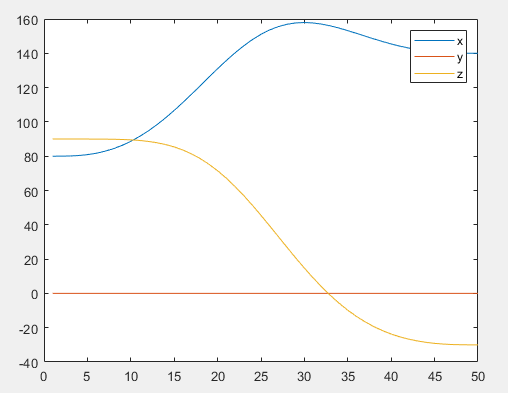
正运动学实现：

给定三个关节角度

clear ; clc; close all;
% 机器人各连杆DH参数
d1 = 0;
d2 = 0;
d3 = 0;

a1 = 80;
a2 = 60;
a3 = 30;

alpha1 = 0.5 * pi;
alpha2 = 0 ;
alpha3 = 0;

% 定义各个连杆，默认为转动关节
%           theta      d        a        alpha 
L1=Link([  0         d1      a1      alpha1]); L(1).qlim=[-pi,pi];
L2=Link([  0         d2      a2      alpha2]); L(2).qlim=[-pi,pi]; L2.offset=pi/3;
L3=Link([  0         d3      a3      alpha3]); L(3).qlim=[-pi,pi]; L3.offset=-pi/3;

robot=SerialLink([L1 L2 L3],'name','robot');

%%正运动学仿真
%给定角度信息
joint(: , 1) = linspace(-pi/6,pi/2,100);
joint(: , 2) = linspace(0,pi/3,100);
joint(: , 3) = linspace(pi/6,pi/2,100);
robot.plot(joint ,'jointdiam',1,'fps',100,'trail','r-')

T = robot.fkine(joint);
T_t = transl(T);
figure
plot(T_t);
legend('x','y','z');
figure
nT=T.T; 
plot3(squeeze(nT(1,4,:)),squeeze(nT(2,4,:)),squeeze(nT(3,4,:)));%输出末端轨迹

运行结果：

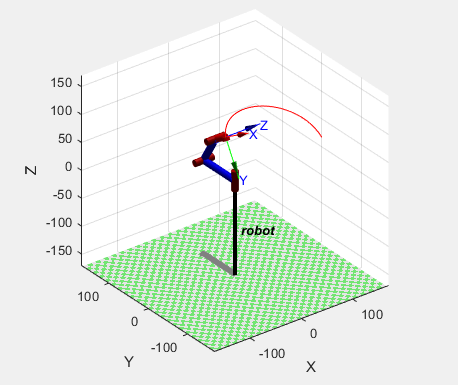
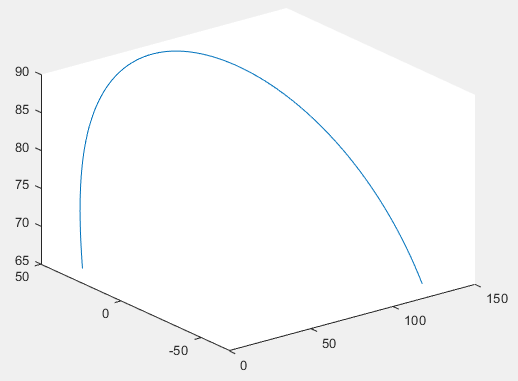
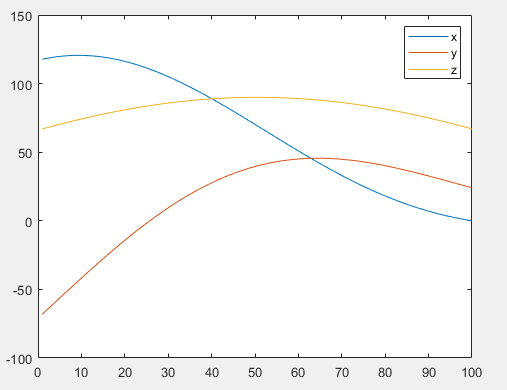
4.平面两连杆机械臂求出存在的各向同性点

5.用牛顿-欧拉法或拉格朗日法建立其动力学方程

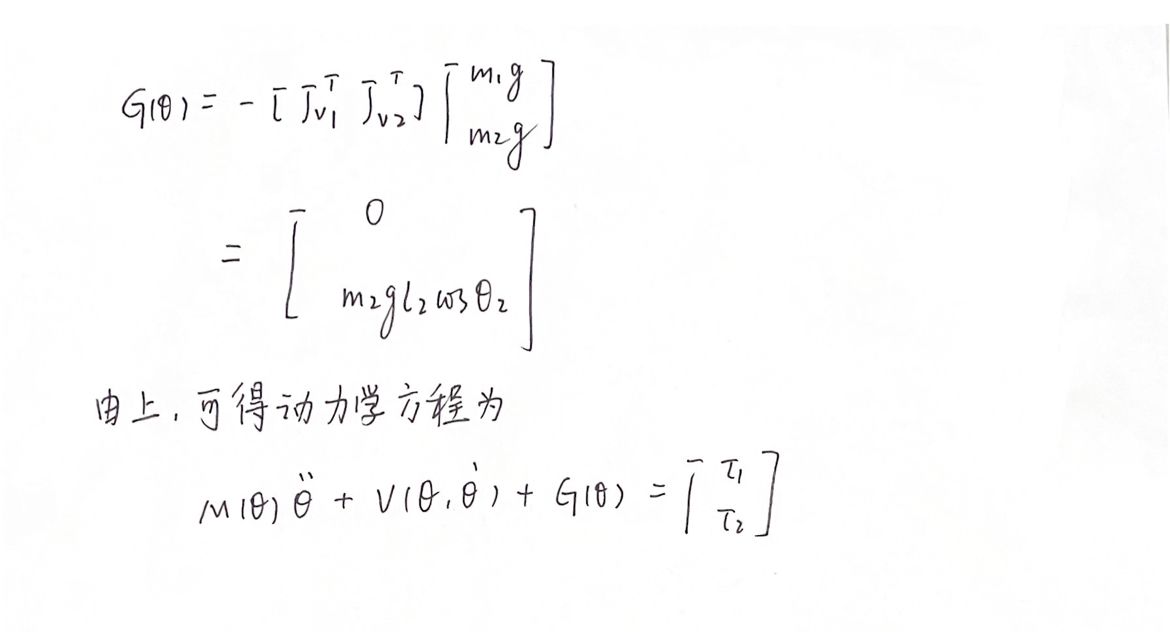
6.证明对于任何负定矩阵kv,这个控制器是稳定的

2022.5.28更新：成绩出来了，得了个良好