激活函数 (activation function)

朴素感知机 vs. 多层感知机 (MLP)

• 一般而言，“朴素感知机”是指单层网络，指的是激活函数使用了阶跃函数的模型
• “多层感知机” (MLP) 是指神经网络，即使用 sigmoid 函数等平滑的激活函数的多层网络
  • 线性函数的问题在于，不管如何加深层数，总是存在与之等效的“无隐藏层的神经网络”。使用线性函数的话，加深神经网络的层数就没有意义了; 因此，神经网络的激活函数必须使用非线性函数以发挥叠加层所带来的优势
  • 同时，神经网络的学习是通过梯度下降来进行参数更新的，而阶跃函数的导数在绝大多数地方均为 0，因此如果使用阶跃函数作为激活函数，则神经网络的学习将无法进行，因此神经网络不适用阶跃函数作为激活函数 (其实同理，$sigmoid$ 函数也很容易产生“梯度消失”的问题，因此现在大多数的激活函数都使用 $ReLU$)

Sigmoid 函数

• Sigmoid 函数即形似 S 的函数. 下面的对率函数是 Sigmoid 函数最重要的代表
  $$h(x)=\frac{1}{1+e^{-x}}$$
  • 优点：Sigmoid 函数的平滑性对神经网络的学习具有重要意义
  • 缺点：计算量较大且容易出现梯度消失。Sigmoid 函数两侧的特征导数接近于 0，这将导致在梯度反向传播时损失的误差难以传递到前面的网络层

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

tanh 函数

$$\tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=2\text{Sigmoid}(2x)-1$$

def tanh(x):
    return 1 - 2 / (np.exp(2 * x) + 1)

ReLU 函数 (Rectified Linear Unit)

• ReLU 函数在 $x>0$ 的部分导数为 1，因此可以无损地进行梯度传递，进而缓减梯度消失现象

def relu(x):
    return np.maximum(0, x)

GELU 函数 (Gaussian Error Linerar Units)

• paper: Gaussian Error Linear Units (GELUs)

---

• 在预训练语言模型中，GELU 可以说是主流的激活函数。它的灵感来源于 ReLU 以及两种正则化方法 Dropout 和 zoneout，主要思想是希望在激活中加入正则化
• ReLU 和 Dropout 都会返回一个神经元的输出，其中，ReLU 会确定性的将输入乘上一个 0 或者 1，Dropout 则是随机乘上 0。而 GELU 也是通过将输入乘上 0 或 1 来实现这个功能，但是输入是乘以 0 还是 1 取决于当前的输入有多大的概率大于其余的输入，具体而言，$x$ 大于其他输入的几率越大，乘以 1 的几率也就越大:
  $$\text{GELU}(x)=P(X\le x)\cdot x$$又因为神经元的输入 $X$ 往往服从正态分布，尤其是深度网络中普遍存在 Batch Normalization，因此
  $$\text{GELU}(x)=x\Phi (x)$$其中，$\Phi (x)$ 为标准正态分布的累积分布函数
  $$\Phi (x)={\int }_{-\infty }^x\frac{e^{-t^2/2}}{\sqrt{2\pi }}dt=\frac{1}{2}\left[1+\mathrm{erf}\left(\frac{x}{\sqrt{2}}\right)\right]$$其中 $\text{erf}$ 为误差函数，表达式如下：
  $$\mathrm{erf}(x)=\frac{2}{\sqrt{\pi }}{\int }_0^x{e}^{-t^2}dt$$代入 $\text{GELU}$ 表达式，可得
  $$\text{GELU}(x)=x\Phi (x)=x\cdot \frac{1}{2}[1+\mathrm{erf}(x/\sqrt{2})]$$
• 因为 $\text{erf}$ 无解析表达式，原论文给出了两种近似表达 (实际上已经有精确的计算函数了)：
  • (1) Sigmoid 近似:
    $$x\Phi (x)\approx x\sigma (1.702x)$$
  • (2) tanh 逼近:
    $$x\Phi (x)\approx \frac{1}{2}x\left[1+\tanh \left(\sqrt{\frac{2}{\pi }}\left(x+0.044715x^3\right)\right)\right]$$

---

MORE

• GELU 的两个初等函数近似是怎么来的

Mish

• paper: Misra, Diganta. “Mish: A self regularized non-monotonic activation function.” arXiv preprint arXiv:1908.08681 (2019).

---

Mish

---

Benchmarks

• CIFAR-10
  
• ImageNet-1k
  
• MS-COCO Object Detection
  

---

Stability, Accuracy, and Efficiency Trade-off

神经网络的前向传播

下面将简单实现三层神经网络的前向传播

• 下图的网络一共由 4 层神经元构成，但实质上只有 3 层神经元有权重，因此将其称为 “3 层网络”。第 0 层对应输入层，第 1，2 层对应中间层，第 3 层对应输出层
  

神经元之间不存在同层连接，也不存在跨层连接。这样的神经网络结构通常称为 “多层前馈神经网络” (multi-layer feedforward neural networks) (“前馈” 并不意味着网络中信号不能向后传，而是指网络拓扑结构上不存在环或回路)

通过矩阵点积运算打包神经网络的运算

引入符号

各层间信号传递的实现

• 如果使用矩阵的乘法运算，则上式可表示为：
  
  • 矩阵 $W$ 的形状：(上一层的神经元个数, 下一层的神经元个数)

• 上述前向传播的过程可以总结为以下代码(完整的代码实现放在后面)：
  

输出层的设计

• 输出层的激活函数不同于隐藏层的激活函数，一般：
  • 回归问题用恒等函数
  • 二元分类问题用 $Sigmoid$ 函数
  • 多元分类问题用 $Softmax$ 函数

$Softmax$ 函数

• $Softmax$ 函数的输出是 $0.0$ 到 $1.0$ 之间的实数。并且， $Softmax$ 函数的输出值的总和是 1。因此可以把 $Softmax$ 函数的输出解释为结果属于某个类别的“概率”
• 即便使用 $Softmax$ 函数，各个元素之间的大小关系也不会改变。求解机器学习问题的步骤可以分为“学习”和“推理”两个阶段。在实际的问题中，由于指数函数的运算需要一定的计算机运算量，因此推理阶段一般会省略输出层的 $Softmax$ 函数 (“学习” 阶段不能省略)

---

• 溢出问题: $Softmax$ 函数的实现中要进行指数函数的运算，但是此时指数函数的值很容易变得非常大。如果在这些超大值之间进行除法运算，结果会出现“不确定”的情况
  • 改进：
    
    式（3.11）说明，在进行 $Softmax$ 的指数函数的运算时，加上（或者减去）某个常数并不会改变运算的结果。这里的 $C^{\prime }$ 可以使用任何值，但是为了防止溢出，一般会使用输入信号中的最大值

---

def softmax(x):
    x = x - np.max(x) # 溢出对策
    return np.exp(x) / np.sum(np.exp(x))

输出层的神经元数量

• 对于分类问题，输出层的神经元数量一般设定为类别的数量
  • e.g., 对于某个输入图像，预测是图中的数字 0 到 9 中的哪一个的问题（10 类别分类问题），可以像图 3-23 这样，将输出层的神经元设定为 10 个
    

批处理

• 以图像大小为 $28\times 28=784$ 的 Mnist 数据集为例，构建三层神经网络，两个隐藏层，第一层 50 个神经元，第二层 100 个神经元，输出为图像属于 10 个类别的概率。单个图像输入时数组形状的变化如下：
  
• 下面考虑打包输入 100 张图像的情况：
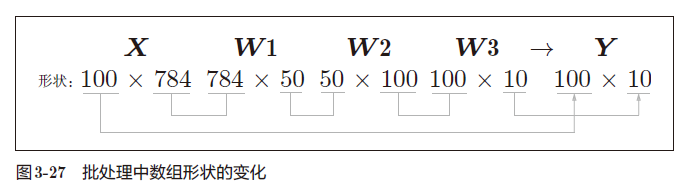  可以看出输入的 100 张图像的结果被一次性输出了，这种打包式的输入数据称为批（batch）

---

• 批处理可以大幅缩短每张图像的处理时间。这是因为大多数处理数值计算的库都进行了能够高效处理大型数组运算的最优化。并且，在神经网络的运算中，当数据传送成为瓶颈时，批处理可以减轻数据总线的负荷（严格地讲，相对于数据读入，可以将更多的时间用在计算上）。也就是说，批处理一次性计算大型数组要比分开逐步计算各个小型数组速度更快

参考文献

• 《深度学习入门 – 基于 Python 的理论与实现》
• BERT 中的激活函数 GELU：高斯误差线性单元