
简介
该用户还未填写简介
擅长的技术栈
未填写擅长的技术栈
可提供的服务
暂无可提供的服务
【张量分析 - 2. 张量场】
流形是一种拓扑空间,它在局部上“看起来”像欧几里得空间。
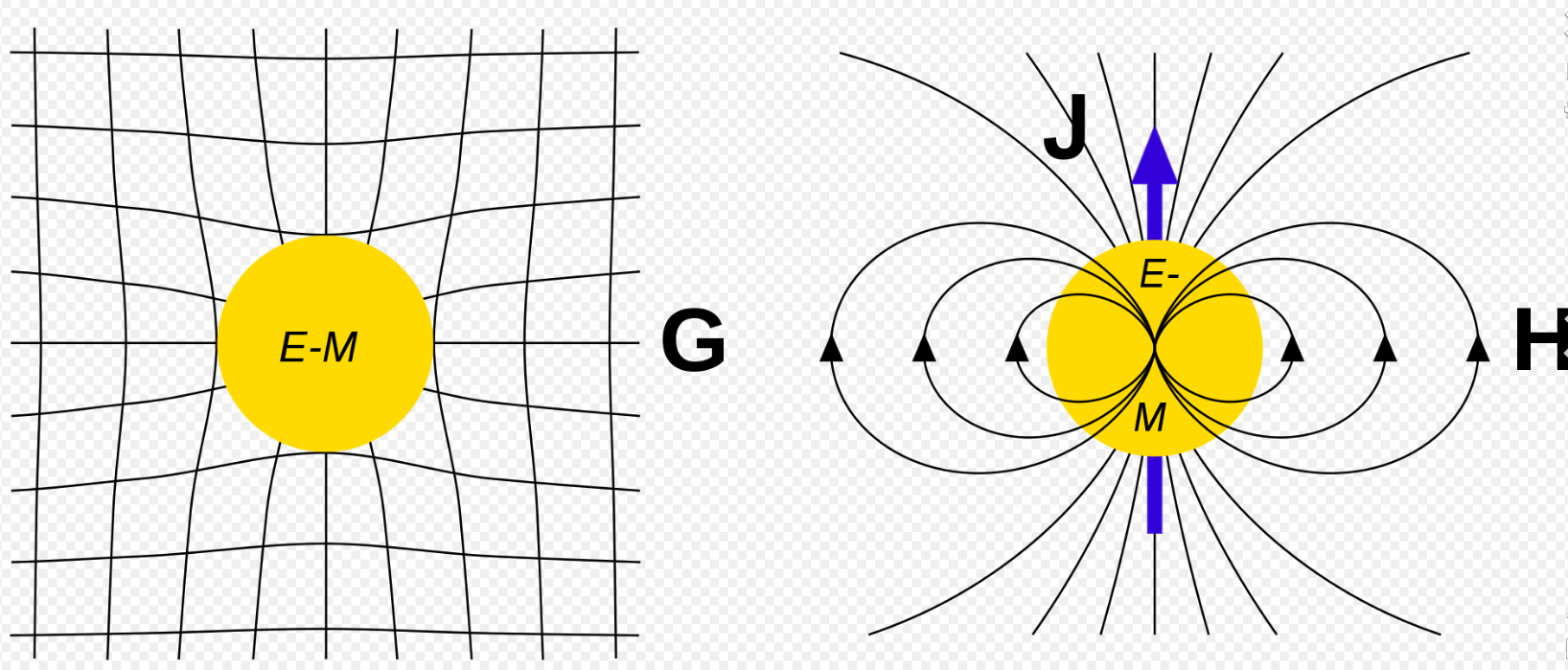
【数值分析 - 3. 特征分解】
矩阵分解(或称为矩阵因式分解)是线性代数中的一个重要概念,在许多领域如机器学习、数据分析、信号处理等都有广泛应用。下面是10种常见的矩阵分解方法:奇异值分解(SVD)特征分解(Eigenvalue Decomposition)QR 分解LU 分解Cholesky 分解极分解(Polar Decomposition)非负矩阵分解(NMF)稀疏编码(Sparse Coding)核范数最小化(Nucle
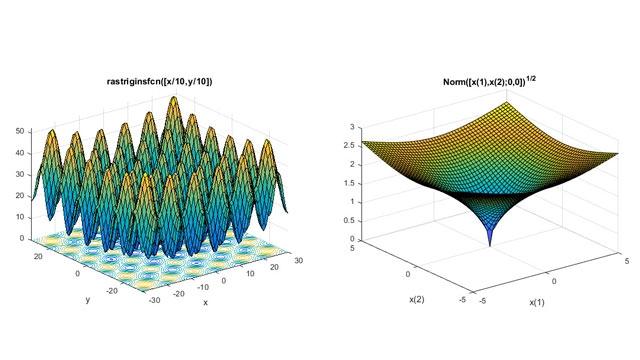
【张量分析 - 4. 应用领域】
在微分几何中,张量算子被用来描述流形上的几何属性,例如曲率和扭曲。例如,黎曼曲率张量就是描述空间扭曲的一个关键对象,它在几何学中有广泛的应用。定义黎曼度量张量(Riemannian Metric Tensor) ,是在黎曼几何中定义的一种 二阶张量 , 用于定义流形上的距离、角度和体积 。在流形上,黎曼度量张量提供了一种 测量局部距离 的方法,它使得我们可以 定义曲线的长度、曲面的面积 等几何概念
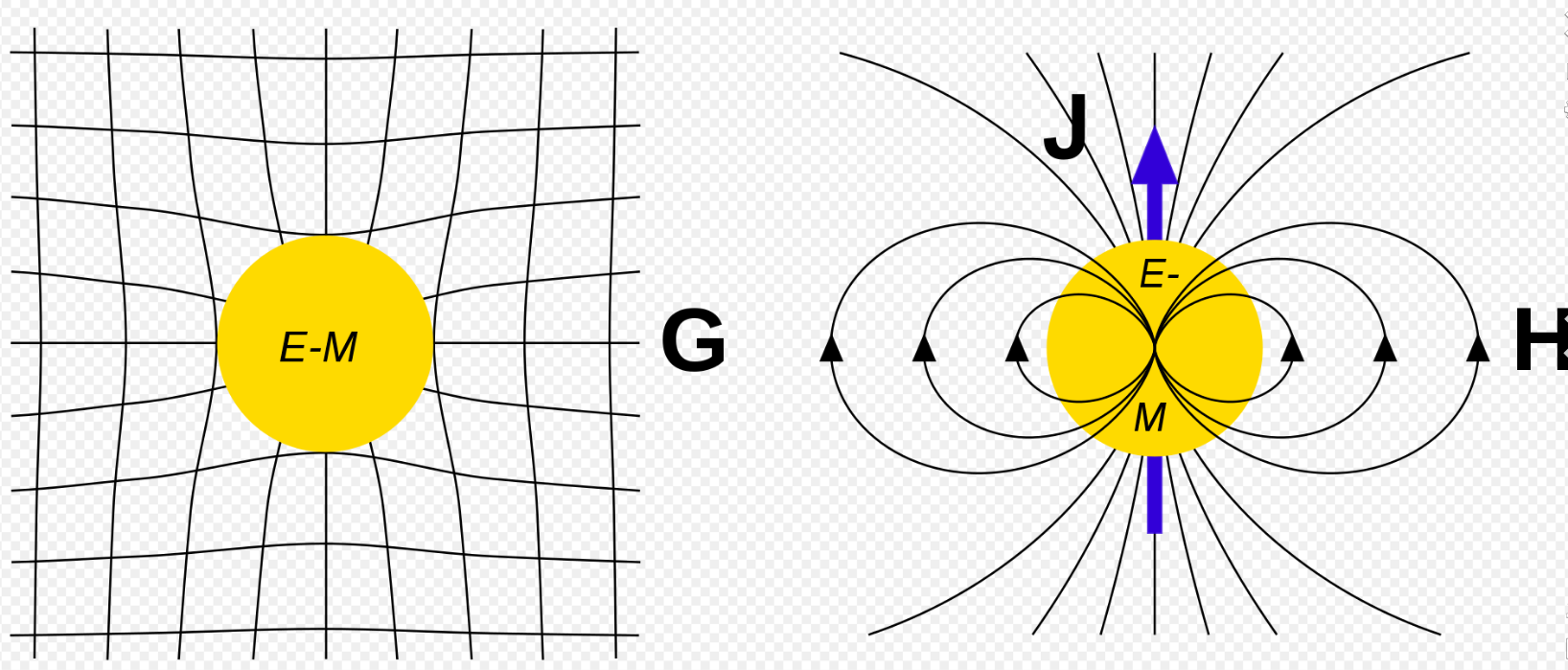
【数值分析 - 2. 矩阵分解】
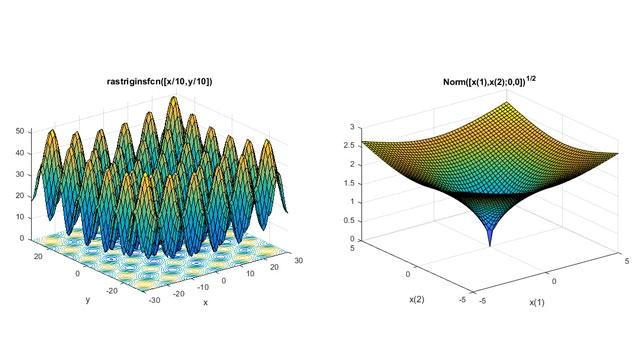
矩阵分解(或称为矩阵因式分解)是线性代数中的一个重要概念,在许多领域如机器学习、数据分析、信号处理等都有广泛应用。
到底了










