1.了解了线性规划问题的内容2.为了让问题能给以计算机计算，我们将模型进行抽象化、统一化，变为线性规划的基本形式3.讲述了经典的线性规划的优化方法：单纯形法。

RST是语言学篇章表示理论中的一个经典表示方法，其思想是将原篇章尽可能进行切分成EDU，然后再两两结合，形成更大的EDU，最后合成整个语篇。于是，我们需要解决的任务有两个：（1）如何切分EDU，（2）如何确定EDU的关系。我们要得到的句子间的关系z，而我们能用到的输入特征有：两个句子的所有词的词向量。其中锚词识别，是用来分割句子的符号，其中以标点符号为主，还有句子中的“并”，“和”这种词。（2）过

对于一个很大的贝叶斯网络，我们需要有一个很高效的方法的快速辨别两个变量之间是不是独立的，但我们这里考虑条件独立性，条件独立性不同于独立性，条件独立性，必须要在某一条件下，考虑另外两个变量之间的独立性。在贝叶斯网络，其联合概率计算是由图来定义的，如下图1.所展示，而如果没有贝叶斯网络，我们无法了解各个变量之间是否有联系，就认为都有联系，于是列出的联合概率公式为0.所示。概率图模型基于图，而图这种数据

总结一下：（1）穷举法无法处理维度大的情况，于是提出（2）单独最优特征最优组合，但这种方法不考虑组合最优，为了改进，提出了（3）SFS和（5）SBS，而为了每次选取是更优的组合，提出（4）GSFS和（6）GSBS，而改进它们一旦决策就不修改的问题，提出了（7）L-R法和（8）广义L-R法。从数据的角度出发，数据的特征并不是全都有用的，总会存在没用的特征，消除这些特征是有必要的，是利于模型去训练的。

1.了解贝叶斯公式。2.了解贝叶斯去决策相关函数和过程。3.根据例子理解朴素贝叶斯分类器在离散变量和连续变量中的设计。

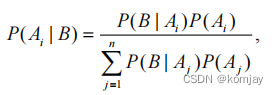
对于一个很大的贝叶斯网络，我们需要有一个很高效的方法的快速辨别两个变量之间是不是独立的，但我们这里考虑条件独立性，条件独立性不同于独立性，条件独立性，必须要在某一条件下，考虑另外两个变量之间的独立性。在贝叶斯网络，其联合概率计算是由图来定义的，如下图1.所展示，而如果没有贝叶斯网络，我们无法了解各个变量之间是否有联系，就认为都有联系，于是列出的联合概率公式为0.所示。概率图模型基于图，而图这种数据

1.显然地，我们之前学习的线性分类法不可能将所有问题进行分类，而实际上，有许多问题是有明显的非线性的决策面进行分类，如下图：2.于是乎，提出非线性分类方法，按思想原理，可分为两种：线性拓展的方法实际上并不对原判别函数的参数进行变动，而是将输入x进行一定的变换，比如二次方化，幂函数化。而我们主要学习非线性思想的几种方法，且这几种方法并不是都是统一的思想原理。

本章的主要内容是要对情绪的形成进行建模，可以理解成如何得到一个情绪向量，基本情感论是认为该向量各个维度独立，是0/1值。维度空间各个维度也独立，但是是连续值。后面的情感模型则希望不对向量各维进行人工定义，而是想通过机器学习来得到。了解情感诱发机制则是帮助我们得到想要的数据信息。

1.了解贝叶斯公式。2.了解贝叶斯去决策相关函数和过程。3.根据例子理解朴素贝叶斯分类器在离散变量和连续变量中的设计。

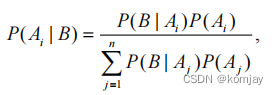
1.显然地，我们之前学习的线性分类法不可能将所有问题进行分类，而实际上，有许多问题是有明显的非线性的决策面进行分类，如下图：2.于是乎，提出非线性分类方法，按思想原理，可分为两种：线性拓展的方法实际上并不对原判别函数的参数进行变动，而是将输入x进行一定的变换，比如二次方化，幂函数化。而我们主要学习非线性思想的几种方法，且这几种方法并不是都是统一的思想原理。