在机器人控制、航天器姿态调整、电力系统稳定、神经网络训练等领域，判断一个系统是否会"失控"至关重要。李雅普诺夫提供了一套**无需实际求解复杂微分方程**就能判定系统稳定性的强大数学工具。

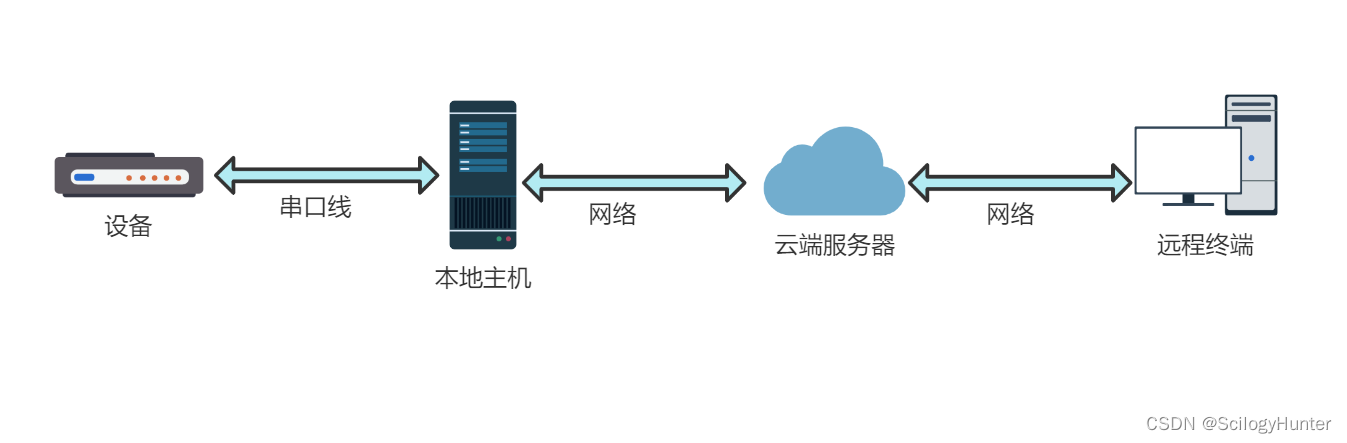
实现原理就是串口转网络，通过网络进行远距离传输，可以是局域网内也可以在广域网内。然后再把网络转成串口，命令行软件（SecureCRT，Xshell，超级终端等）连接这个远程串口和连接本地串口在协议上完全是没区别的，但速度上可能会有降低。...

在实时操作系统 (RTOS) 中，线程是最小的执行单元。线程在 RTOS 中对于管理需要同时运行的任务至关重要。每个线程都有其自己的堆栈，这是其执行上下文的重要组成部分。RTOS 调度程序根据优先级决定在任何给定时间运行哪个线程。高优先级线程可以抢占低优先级线程，以确保关键任务按时完成。线程可以使用消息队列和信号量等线程间通信机制进行通信。正确的线程管理是实现嵌入式系统中实时性能的关键。

物互联时代已经到来万物互联时代的到来，智能家电、个人智能穿戴设备、智慧城市、智能制造等的普及都给我们的生活和工作带来了极大的便利和生产力的提高。从全球范围来看，目前产业物联网与消费性物联网基本同步发展，据 GSMA intelligence 预测，从2018-2025年，产业物联网连接数将实现3.7倍增长，消费物联网连接数将实现2.1倍增长，到2023年，全球物联网设备联网数量将有望超过200亿个

翼辉信息（武汉）培训交流活动圆满结束发布于2016年12月22日12月20日，翼辉信息进一步聚集行业客户资源，在武汉华中科技大学举办了“SylixOS操作系统行业客户培训交流活动”。包括军工、运动控制、电力、高等教育等行业在内的二十多家客户应邀参加此次培训交流活动。本次活动从SylixOS自主实时操作系统的介绍开始逐步展开，就支持SMP的大型实时操作系统的功能、RealEvo集成开发环境、Real

SylixOS通过北航软件测评实验室第三方测试发布于2017年02月07日2017年1月15日，北京航空航天大学软件测评实验室（以下简称“北航软件测评实验室”）依照GJB7706-2012《军用嵌入式操作系统测评要求》完成了对翼辉信息研发的大型开源嵌入式实时操作系统SylixOS的第三方软件评测，并出具了测试报告。报告的测试结论说明SylixOS实时操作系统内核满足GJB7718-2012《军用嵌

翼辉信息与龙芯完成产品兼容互认证发布于2020年05月08日近日，翼辉信息的SylixOS嵌入式操作系统与龙芯的3A3000和2K1000平台完成产品兼容互认证。测试结果显示，翼辉信息的SylixOS嵌入式操作系统在龙芯3A3000和2K1000平台上顺利安装，运行良好，且整体系统运行稳定。北京翼辉信息自主研发的“SylixOS嵌入式实时操作系统“拥有32位和64位版本，支持AMP和SMP等多种运

在实时操作系统（RTOS）中，中断对于响应实时事件至关重要。中断是一种信号，它会暂时停止CPU的当前操作以执行特定任务。中断确保系统可以在没有延迟的情况下处理关键事件，例如输入/输出操作、传感器读取或与其他设备的通信。当发生中断时，CPU会保存其当前状态并执行中断服务程序（ISR）。ISR 是一个处理中断的小型预定义程序。有效管理中断对于保持系统的实时性能至关重要。中断延迟是指CPU响应中断所需的

翼辉信息 SylixOS 操作系统全面支持晶心科技 AndesCore™ A25 系列 RISC-V 处理器发布于2019年11月15日【中国北京】2019年11月14日－开源实时操作系统SylixOS的供应商北京翼辉信息技术有限公司（以下简称：翼辉信息）,宣布与RISC-VCPU处理器核心的领导供货商晶心科技合作,SylixOS操作系统全面支持AndesAndesCore6敬A25系列处理器。

翼辉信息与飞腾完成产品兼容性互认证发布于2020年05月08日近日，翼辉信息的 SylixOS 嵌入式操作系统与飞腾的 FT-1500A/4 和 FT-2000A/2 处理器完成产品兼容互认证。测试结果显示，翼辉信息的 SylixOS 嵌入式操作系统在飞腾的 FT-1500A/4 和 FT-2000A/2 处理器上顺利安装，运行稳定。北京翼辉信息自主研发的“SylixOS 嵌入式实时操作系统“拥有