在目标检测领域，通常将网络的输出转为直观的检测框信息这一过程称为decode，就是根据网络的输出获取直观的检测框信息。那么encode就是将检测框信息（通常为ground-truth bounding box的坐标、宽高信息）转化为形为网络输出的信息，便于网络损失函数的求解。两阶段检测的框架就是先通过启发式方法（selective search）或者CNN网络（RPN)产生一系列稀疏的候选框，然后

如果现在有一个主线程两个子线程，子线程的target是f1()，相当于会把f1()单独克隆出2份（注意：其他和f1()函数不相关的代码是不会被克隆的），这两个子线程只执行f1()，执行完f1()就死掉！和主线程互不影响，若f1()中y有调用到其他函数比如f2()，则f2（）函数也会被克隆两份出来，这样就保证每个线程拥有了自己的函数堆栈，跑f1()时调用就可以正常执行！每个线程间是相互独立的互相看不

它的主要思想是将高维的数据映射到低维，使该低维的数据能够反映原高维数据的某些本质结构特征。可以简单的将流形理解成二维空间的曲线，三维空间的曲面在更高维空间的推广。下图是三维空间中的一个流形，这是一个卷曲面，像一个瑞士卷一样，而3维空间中的曲面可以看做是2维的流形，因为曲面是2维的。n维空间中的m维流形就是具有m维几何形状的一个子集，在这里，m小于n。图上所标注的两个圈圈，在流形（把卷展开）上本距离

利用下面两条原则，便可大杀四方。

神经网络中的多维矩阵乘积运算：多维矩阵乘积运算乘积两项的维度都应该是相同的，如果有论文中有遇到矩阵乘积的两项维度不一致，那就考虑它计算时是使用了广播机制（如YOLACT）。所有大于二维的，最终都是以二维为基础堆叠在一起的！！所以在矩阵运算的时候，其实最后都可以转成我们常见的二维矩阵运算，遵循的原则是：在多维矩阵相乘中，需最后两维满足shape匹配原则，最后两维才是有数据的矩阵，前面的维度只是矩阵的

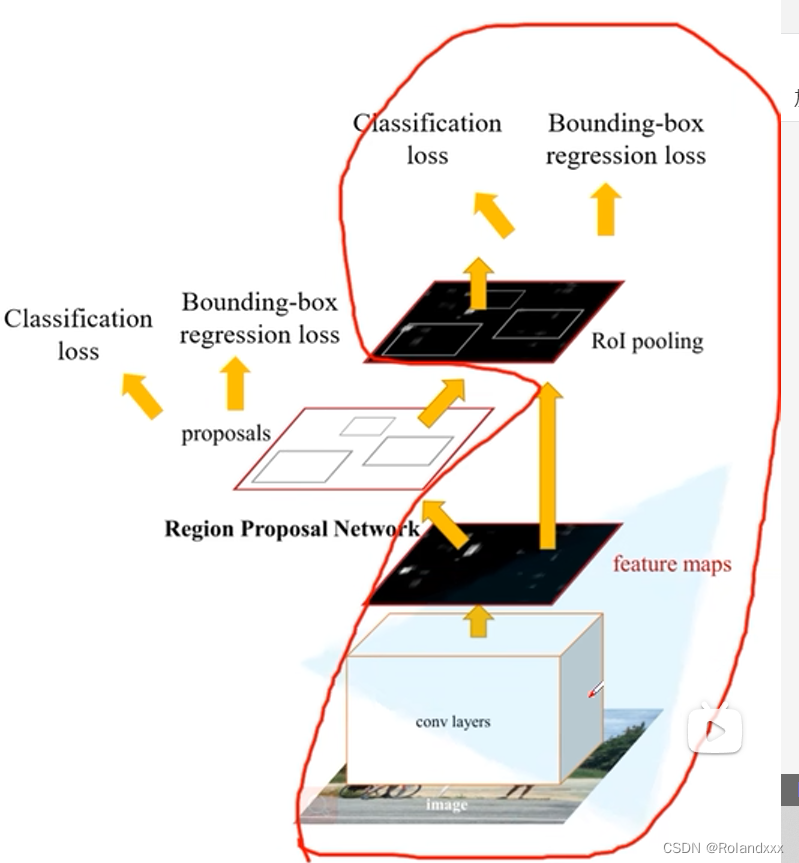
在目标检测领域，通常将网络的输出转为直观的检测框信息这一过程称为decode，就是根据网络的输出获取直观的检测框信息。那么encode就是将检测框信息（通常为ground-truth bounding box的坐标、宽高信息）转化为形为网络输出的信息，便于网络损失函数的求解。两阶段检测的框架就是先通过启发式方法（selective search）或者CNN网络（RPN)产生一系列稀疏的候选框，然后

想要充分理解粒子滤波算法，必须得从贝叶斯滤波器开始理解起来，因为卡尔曼滤波和粒子滤波都是基于此的。动态模型是指两个函数或者说两个模型（状态模型和观测模型）：一个函数的输出为当前时刻的状态，输入为上一时刻的状态和噪声。另一个函数的输出是当前时刻的观测，输入为当前时刻的状态（这个状态是更新调整后的）和噪声。卡尔曼滤波限制噪声时服从高斯分布的，但是粒子滤波可以不局限于高斯噪声，原理上粒子滤波可以驾驭所有

它的主要思想是将高维的数据映射到低维，使该低维的数据能够反映原高维数据的某些本质结构特征。可以简单的将流形理解成二维空间的曲线，三维空间的曲面在更高维空间的推广。下图是三维空间中的一个流形，这是一个卷曲面，像一个瑞士卷一样，而3维空间中的曲面可以看做是2维的流形，因为曲面是2维的。n维空间中的m维流形就是具有m维几何形状的一个子集，在这里，m小于n。图上所标注的两个圈圈，在流形（把卷展开）上本距离

极几何描述了同一场景或者物体在两个视点图像间的对应关系。下图中的O1和O2分别是两个相机的光心，即摄像机坐标系的原点。由下图可知给定了一个三维空间下的P点，虽然不知道对应的成像平面上像素点p和p’在哪个位置，但是我知道它一定在l和l’这两条极线上。这样就不会全图去找了，只用在极线上去搜索了。再比如给定一个图像上的p点，找另一个图像上对应的p’点就可以通过极几何约束，将搜索范围缩小到对应的极线上本质

求矩阵A的特征值及特征向量问题就转化为求解多项式方程以及齐次线性方程组的通解问题。，若3是A的一个特征值，求：y及A的其他特征向量。的另一个根1，故A的全部特征值为-1，1，1，3。2、n阶方阵A的特征值，就是使齐次线性。因为3是A的一个特征值，所以3必为。3、A的特征矩阵也可以表示为。特征多项式也可以表示为。是矩阵A的特征值，x是A的属于。成为方阵A的特征值，非零向量。，特征值问题是对方阵而言的