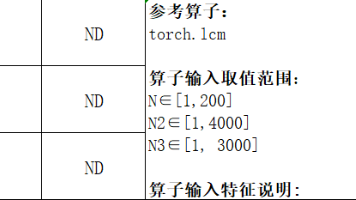
具体描述是：参考算子：torch.lcm算子输入取值范围：N∈[1,200]算子输入特征说明:输入x2应与x1 Shape一致，如果不一致，则对应的维度为1，可以广播成与x1 Shape一致，需要考虑广播实现。N~N3均可能为非32的整倍数，需要考虑非对齐场景。int64类型数据取值会超出int32取值范围，注意不要使用Cast强转int64到int32参考实现是。

博弈 逆序对 循环移位两个人分别操作自己的排列ab，每次可以交换两个元素，要求交换之后∑ai​bi​变大。轮流进行，如果一个人没法操作了，就输了。每次询问会把一个人的排列的一个区间循环移位，然后需要输出此时先手必胜还是必败注意到∑ai​bi​最大就是两个排列完全一样，进一步，越接近完全一样，式子就越大。所以一个人每次交换两个元素，想让式子变大，1必须是逐步排序的一个过程，也就是要至少消除一个逆序对

构造 二分图 拆位给一个序列A，给一堆约束xyz，要求Ax​⊕Ay​z需要构造一个A序列，使得∑Ai​最小，或报告无解。位运算，尤其是异或，他是不进位的，不同位之间完全没有影响，考虑拆位。对于每一位就是一个只有01的情况。这样约束只有两类，z0/1，也就是Ax​Ay​在这一位相同0，或不同1。利用这个关系建图，会发现我们实际上就得到了一个二分图。于是问题转化成给一堆关系，每个关系是xy是同一类，或

线段树每次从bi​开始，给长度为ai​的子数组都加1，这是个循环数组，超过n了会回到开头。每次加的元素ai​是从数组里取的，也就是需要动态修改，查询。ai​很大的话，其实加操作就是一个后缀，一个前缀，加中间多段完整的，每段完整的都一样，三次区间加即可。线段树维护。

概率dp/期望dp每一次投出一个点数y，范围1n，如果比x小，结束。如果比x大，y=x，总分加ay​。问总分的期望？两个思路，一是可以概率dp，因为总分的期望等于每个ai​的贡献的期望和，可以正着dp，算出来达到每个i的概率，这显然就是个前缀和优化。但这个并不自然求期望，还是考虑期望dp，dpi​表示当前xi开始玩，剩下的得分的期望。当前投一次有n种取值，只有投出比i大的才有意义，转移就是dpu​

具体描述是：参考算子：torch.lcm算子输入取值范围：N∈[1,200]算子输入特征说明:输入x2应与x1 Shape一致，如果不一致，则对应的维度为1，可以广播成与x1 Shape一致，需要考虑广播实现。N~N3均可能为非32的整倍数，需要考虑非对齐场景。int64类型数据取值会超出int32取值范围，注意不要使用Cast强转int64到int32参考实现是。

模拟两个序列每次可以选一个位置，如果ai​bi​则给ai​减一。问最多进行多少次操作计算∑maxai​−bi​0即可。