视觉语言导航基础入门

本文对于了解具身智能是干嘛的会有一些帮助

本文对于了解具身智能是干嘛的会有一些帮助

本文对于了解具身智能是干嘛的会有一些帮助

本文对于了解具身智能是干嘛的会有一些帮助

算出一条满足约束的最优轨迹。什么是最优？平滑性舒适性尽可能短，耗时少约束：（1）轨迹连续性（2）无碰撞（3）交规（4）车辆动力学衡量轨迹质量往往用cost function表示sfta0a1ta5t5sfta0​a1​t...a5​t5a0a1a5都是未知常数(a_{0},a_{1},...,a_{5}都是未知常数)a0​a1​...a5​都是未知常数Jw1f˙2w2f¨2。

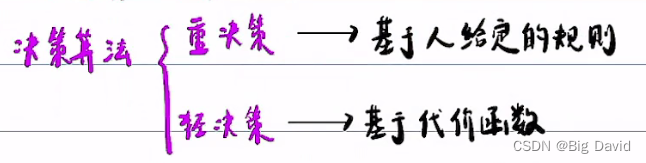
（2）有粗解，通过设计代价函数，可以使粗解“满足”硬约束（碰撞、最小曲率），这样使二次规划求解成功的机率大大增加（因为粗解在凸空间内部，所以该凸空间的“扭曲”程度至少有粗解兜底）大大缓解了基于人为规则的决策所造成的凸空间扭曲情况。轻决策：无先验规则，空间离散化，设计cost function,动态规划算法求解离散空间的最优路径，该最优路径开辟凸空间。（2）在感知不强的情况下仍然能做决策（融合了人的

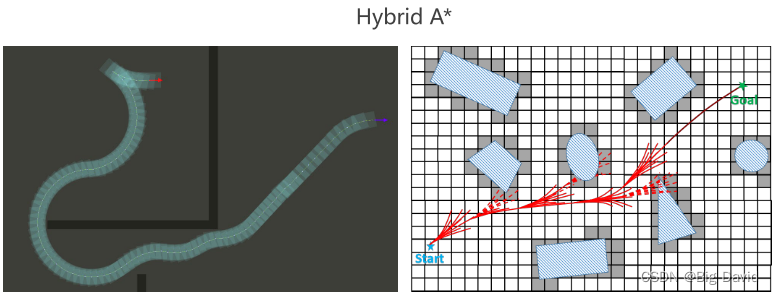
本文对高飞老师的移动机器人运动规划课程第一章做了学习记录，方便日后复习回顾😘

结合即得到二次规划下的最优路径，再转化为Cartesian坐标，路径规划完成。接着上一讲学习记录b站老王对自动驾驶规划系列的讲解。二次规划的求解空间就在此凸空间中搜索。则分段加加速度约束为。

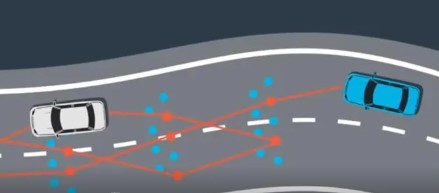
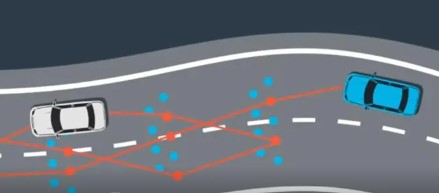
回顾上一节：参考线，提供光滑的frenet坐标轴以host在reference line的投影为坐标原点，建立frenet坐标系。障碍物投影，生成SL图确定规划的起点定位得到的host_x,host_y投影到referenceline，得到SL坐标(0,l0l_0l0​)，以此点为路径规划的起点这样做是错的考虑控制是不完美的规划以100ms周期执行，在上个周期已经规划出轨迹。正确的做法：以（S0l