P10307 「Cfz Round 2」Binary

题目描述

给定 $n+1$ 个整数 $a_0\dots a_n$。

对于整数 $u$，设它在二进制下为 $1$ 的位分别为 $k_1,k_2\dots k_m$，那么它的权值 $f(u)=a_{k_1}\oplus a_{k_2}\oplus \cdots \oplus a_{k_m}$。此处的二进制位的编号从右到左，依次为 $0,1,2\dots$。其中 $\oplus$ 表示 按位异或 符号。

你想要知道有多少个 $0\le u\le 2^n-1$ 使得 $f(u)=f(u+1)$。为了方便，请你用 二进制形式 输出答案（不取模）。

请注意：输出不能包含前导 $0$，除非答案为 $0$。

输入格式

本题有多组测试数据。

第一行输入一个整数 $T$，表示测试数据组数。

接下来依次输入每组测试数据。对于每组测试数据：

• 第一行输入一个正整数 $n$。
• 第二行输入 $n+1$ 个整数 $a_0\dots a_n$。

输出格式

对于每组数据，输出一行一个二进制整数，表示答案。

再次提示：输出不能包含前导 $0$，除非答案为 $0$。

输入输出样例 #1

输入 #1

5
2
0 1 2
3
1 3 3 1
4
2 2 5 4 2
5
7 0 3 4 0 1
6
5 2 1 8 6 0 9

输出 #1

10
1
100
11
0

说明/提示

「样例解释 #1」

对于第 $1$ 组数据，

• $(0{)}_{10}=(0{)}_2$，所以 $f(0)=0$；
• $(1{)}_{10}=(1{)}_2$，所以 $f(1)=a_0=0$；
• $(2{)}_{10}=(10{)}_2$，所以 $f(2)=a_1=1$；
• $(3{)}_{10}=(11{)}_2$，所以 $f(3)=a_0\oplus a_1=0\oplus 1=1$；
• $(4{)}_{10}=(100{)}_2$，所以 $f(4)=a_2=2$。

这其中有 $f(0)=f(1)$，$f(2)=f(3)$，所以输出 $(2{)}_{10}=(10{)}_2$。

「数据范围」

设 $\sum n$ 表示单个测试点中 $n$ 的和。

对于所有数据，$1\le T\le 10^3$，$1\le n\le 2\times 10^5$，$\sum n\le 6\times 10^5$，$0\le a_i\le 2^{30}-1$。

只有你通过本题的所有测试点，你才能获得本题的分数。

C++实现

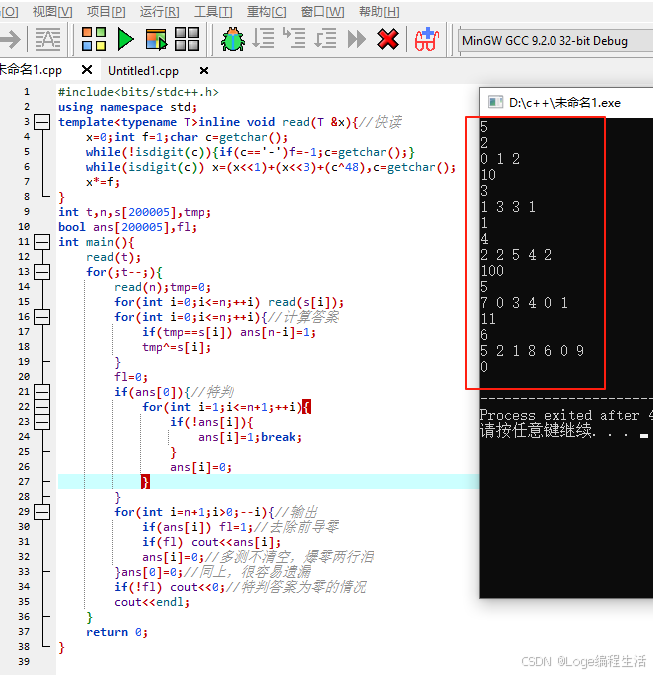
#include<bits/stdc++.h>
using namespace std;
template<typename T>inline void read(T &x){//快读
	x=0;int f=1;char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
	x*=f;
}
int t,n,s[200005],tmp;
bool ans[200005],fl;
int main(){
	read(t);
	for(;t--;){
		read(n);tmp=0;
		for(int i=0;i<=n;++i) read(s[i]);
		for(int i=0;i<=n;++i){//计算答案
			if(tmp==s[i]) ans[n-i]=1;
			tmp^=s[i];
		}
		fl=0;
		if(ans[0]){//特判
		    for(int i=1;i<=n+1;++i){
		        if(!ans[i]){
		            ans[i]=1;break;
		        }
		        ans[i]=0;
		    }
		}
		for(int i=n+1;i>0;--i){//输出
			if(ans[i]) fl=1;//去除前导零
			if(fl) cout<<ans[i];
			ans[i]=0;//多测不清空，爆零两行泪
		}ans[0]=0;//同上，很容易遗漏
		if(!fl) cout<<0;//特判答案为零的情况
		cout<<endl;
	}
	return 0;
}

后续

接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现，记录日常的编程生活、比赛心得，感兴趣的请关注，我后续将继续分享相关内容