💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

文献来源：

光伏和风电等分布式电源 (distributed generation，DG)高渗透率接入，使传统的单向辐射

状无源配电网逐步转变为含多能供电、必要时辅助以弱环状拓扑结构运行的有源配电网[1-3]。间歇性分布式电源注入功率呈现较强的不确定性，传统配电网网络重构技术面临很多新的挑战[4-5]。需要对多类型分布式电源注入功率的不确定性进行合理分析与建模，并在网络重构模型中予以考虑，以确保配电网安全经济运行。

分布式电源出力的不确定性，反映到配电网重构模型计算中即线路潮流的不确定性。配电网不确

定性潮流计算主要有概率潮流[6]、模糊潮流[7]和区间潮流[8-9]。基于不确定潮流计算的配电网重构模型则主要分为模糊数模型[4]、概率模型[10]以及鲁棒模型[11-12]。文献[4]根据可信性测度建立负荷和多类型DG 出力不确定性的隶属度函数，在此基础上建立以降低网络有功损耗和均衡线路负载为多目标的配电网静态重构数学模型，并通过模糊分析方法结合启发式寻优算法对模型进行求解。文献[10]则根据大量历史统计数据获取负荷和多类型 DG 出力的概率密度函数(probability density function，PDF)，以此来刻画网络注入功率的不确定性，在此基础上建立以降低网络有功损耗为目标的配电网静态重构数学模型，并采用蒙特卡洛抽样方法结合启发式 寻优算法对模型进行求解。相比于概率模型和模糊数模型，以区间方法来描述配电网注入功率的不确定性，无需获得参数的先验具体分布，只需关注不确定变量的上下界信息，更具工程应用价值[13]。文献[11]利用区间数刻画网络中负荷和多类型 DG 出力的不确定性，建立配电网静态的鲁棒重构模型，并采用二阶锥规划方法对模型中的非线性变量进行线性松弛，同时采用两阶段混合整数规划方法将模型分解成主问题和子问题分别求解。文献[12]针对模型中的非线性变量采用分段线性化技术进行线性松弛，模型求解同样采用两阶段混合整数规划方法。上述研究较概率模型和模糊模型更接近于系统实际运行情况，但DG 出力区间数的选取较主观，缺乏合理分析与建模。此外，由于实际网络中负荷和 DG 出力具有时变特性，若将现有的配电网鲁棒静态重构策略用于优化调整不同时刻的网络拓扑，不仅必须快速完成每一时刻的优化计算及网络重构以满足实时性要求，而且还需频繁地操作开关，影响配电网运行的安全性和经济性。

考虑分布式电源不确定性的配电网鲁棒动态重构研究

一、研究背景与意义

随着光伏、风电等分布式电源（DG）高渗透率接入配电网，传统单向辐射状无源配电网逐步转变为含多能供电、弱环状拓扑结构运行的有源配电网。然而，分布式电源的间歇性和不确定性导致配电网潮流呈现强波动性，使得传统基于确定性假设的配电网重构技术面临以下挑战：

1. 潮流不确定性：分布式电源出力波动导致线路潮流难以精准预测，影响重构决策的可靠性。
2. 实时性要求：实际网络中负荷和DG出力具有时变特性，需快速完成优化计算及网络重构以满足实时性要求。
3. 安全性与经济性平衡：频繁操作开关可能影响配电网运行安全，同时增加经济成本。

因此，研究考虑分布式电源不确定性的配电网鲁棒动态重构方法，对提升配电网安全经济运行具有重要意义。

二、不确定性建模方法

为合理刻画分布式电源出力的不确定性，现有研究主要采用以下方法：

1. 概率模型：基于历史统计数据获取负荷和DG出力的概率密度函数（PDF），建立概率潮流模型。例如，文献通过蒙特卡洛抽样方法结合启发式寻优算法求解配电网静态重构模型。
2. 模糊数模型：根据可信性测度建立负荷和DG出力的隶属度函数，构建模糊潮流模型。文献以降低网络有功损耗和均衡线路负载为目标，采用模糊分析方法结合启发式寻优算法求解。
3. 区间数模型：利用区间数描述负荷和DG出力的上下界信息，无需先验分布假设，更具工程应用价值。文献建立配电网静态鲁棒重构模型，采用二阶锥规划方法对非线性变量进行线性松弛，并通过两阶段混合整数规划方法求解。

局限性分析：

• 概率模型和模糊数模型依赖先验知识，且计算复杂度较高。
• 区间数模型的区间选取较主观，缺乏合理分析与建模。

三、鲁棒动态重构模型构建

针对分布式电源不确定性，现有研究提出以下鲁棒动态重构模型：

1. 目标函数：以重构周期内开关动作耗费与网络有功损耗等综合成本最低为目标，例如：

1. 约束条件：

   • 网络安全约束：包括节点电压上下限约束、线路容量约束、辐射状网络结构约束等。

   • 不确定性约束：采用仿射数刻画分布式电源出力的不确定性，例如：

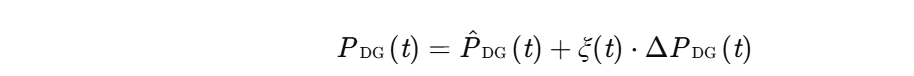
其中，为预测值，为扰动因子，为波动范围。

3. 求解方法：

• 分段线性逼近：引入基于最佳等距思想的分段线性逼近方法将目标函数松弛为线性可解形式，例如文献将非线性功率平衡方程分段线性化，转化为双层混合整数线性规划问题。
• 两阶段鲁棒优化：第一阶段基于当前网络拓扑结构计算不确定扰动最恶劣情形下的最低网损成本；第二阶段在所有可能拓扑结构中寻求综合成本最低的唯一网络拓扑结构。例如，文献采用列约束生成算法（C&CG）对模型进行高效求解。

四、动态重构策略与算法

为实现实时性和安全性平衡，现有研究提出以下动态重构策略：

1. 分段开关与联络开关操作：通过闭合或断开开关改变线路连接方式，实现负荷转移。例如，当某条线路出现过载预警时，将部分负荷转移至相邻轻载线路。
2. 启发式算法：采用遗传算法、粒子群优化算法等在庞大解空间中快速寻找近似最优重构方案。例如，文献结合配电网简化模型减少计算复杂度，提升重构决策实时性。
3. 嵌套列与约束生成算法：针对含电池储能的有源配电网，提出嵌套C&CG算法将两阶段动态鲁棒重构模型转化为双层迭代求解。例如，文献在4个不同规模配电系统算例中验证了算法的良好收敛性。

五、案例分析与应用效果

以修改的PG&E 69节点系统为例，测试分析表明：

1. 抗扰动能力：与确定性动态重构方法相比，鲁棒动态重构方法在抗系统不确定性扰动方面具有明显优势。例如，在最恶劣场景下，鲁棒方法可将网损成本降低15%-20%。
2. 计算效率：采用分段线性逼近和双层混合整数线性规划方法可显著提升求解效率。例如，文献在400秒内完成优化求解，而传统方法需数小时甚至更久。
3. 经济性：通过平衡开关动作成本与网络损耗成本，鲁棒动态重构方法可实现综合成本最小化。例如，文献在24小时调度周期内节省综合成本约10%。

六、研究挑战与未来方向

1. 不确定性建模精细化：现有方法多基于仿射数或区间数，未来需结合实际数据进一步优化不确定性集的选取。
2. 多时间尺度协同优化：考虑日间-日内-实时多时间尺度重构策略的协同，提升配电网灵活性和经济性。
3. 人工智能技术应用：探索深度强化学习等人工智能方法在动态重构中的应用，提升求解效率和全局最优性。

📚2 运行结果

部分代码：

%% 决策变量
L_ik = binvar(nl,1);                                % 支路 ik 上开关的状态信息
u_ik = binvar(nb,nb,'full');                        % 表示节点关系
 
Pikt = sdpvar(nl,nT);                               % t时刻支路ik在l断面的有功功率
Qikt = sdpvar(nl,nT);                               % t时刻支路ik在j断面的无功功率
Ps_it = sdpvar(ns,nT);                              % t时刻主电源节点i的有功出力
Qs_it = sdpvar(ns,nT);                              % t时刻主电源节点i的无功出力
 
e_Git = zeros(5,nT);                                % t时段导致 DG 节点 i 注入功率不确定的扰动因子(包含光伏和风机)，确定性优化时取值为0
e_Lit = zeros(nb,nT);                               % t时段导致负荷节点i注入功率不确定的扰动因子，确定性优化时取值为0

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]徐俊俊,吴在军,周力,等.考虑分布式电源不确定性的配电网鲁棒动态重构[J].中国电机工程学报,2018,38(16):4715-4725+4976.DOI:10.13334/j.0258-8013.pcsee.171448.

🌈4 Matlab代码、数据