在AI高速发展的时代，作为人工智能的一个重要分支，机器学习的热度大家有目共睹。要是能够在文献里用上一二，对论文质量提升较大。我们将介绍使用LASSO和随机森林（RandomForest)筛选特征基因。本期介绍LASSO。

---

小短文了解LASSO

一、LASSO 是什么？

LASSO 的全称是 “Least Absolute Shrinkage and Selection Operator”（最小绝对收缩与选择算子），是一种带 “正则化” 约束的回归方法。简单说，它的核心功能有两个：

• 收缩（Shrinkage）：让不重要的特征系数 “变小”

• 选择（Selection）：让一部分特征的系数直接 “变成 0”，相当于把这些特征从模型中 “剔除”

这种 “一边建模、一边筛选特征” 的能力，让它在高维数据（比如基因表达数据，特征数远多于样本数）中特别实用。

二、LASSO 的核心原理：L1 正则化

传统的线性回归（或逻辑回归）在特征太多时，容易出现 “过拟合”（模型太复杂，只记住了训练数据的细节，泛化能力差）。而 LASSO 通过加入一个 “L1 正则化” 约束，解决了这个问题。

通俗理解：

假设我们要通过 1000 个基因（特征）预测疾病状态（比如 “病例组” vs “对照组”），传统回归可能会给每个基因分配一个系数，但很多系数可能是 “噪音”（其实和疾病无关）。

LASSO 会在模型训练时加入一个 “惩罚项”：惩罚系数绝对值的总和（这就是 L1 正则化）。这个惩罚会 “迫使” 不重要的特征系数被 “压缩” 到 0—— 系数为 0，意味着这个特征对模型没有贡献，相当于被 “筛选掉” 了。

最终留下的，就是系数非零的 “关键特征”（比如与疾病相关的核心基因）。

三、LASSO 为什么适合基因数据筛选？

在生物信息学分析中，我们常遇到这样的情况：样本量较少、特征较多

这时候用传统回归会有两个麻烦：

• 特征太多，模型复杂到 “学不透”（过拟合）

• 无法判断哪些特征（基因）是真正和疾病相关的（传统回归不会主动剔除特征）

而 LASSO 的优势正好能解决这两个问题：

• 它能在 “控制模型复杂度” 的同时，自动把无关特征的系数压缩到 0，直接完成 “特征筛选”

• 最终留下的特征少而精，模型更简单、解释性更强（比如筛选出 3-5 个核心基因，比 “用 1000 个基因建模” 更容易理解）

四、关键参数：lambda（λ）—— 控制筛选 “严格度”

LASSO 的核心是一个叫 “lambda（λ）” 的参数，它决定了 “惩罚力度”：

• λ 越小：惩罚越轻，模型保留的特征越多（可能保留噪音，过拟合风险高）；
• λ 越大：惩罚越重，模型会 “剔除” 更多特征（可能把有用的特征也删掉，欠拟合风险高）。

因此，选对 λ 是 LASSO 分析的关键。实际中，我们常用 “交叉验证”（比如 10 折交叉验证）来确定最优 λ：通过多次分割数据、训练模型，找到 “预测误差最小” 时对应的 λ（称为lambda.min），这个 λ 能平衡 “筛选精度” 和 “模型泛化能力”。

五、总结：LASSO 的核心价值

简单说，LASSO 就像一个 “智能筛选器”：面对成百上千的特征（比如基因），它能自动挑出那些 “真正有价值” 的变量，同时简化模型、避免过拟合。这也是为什么在基因表达、蛋白质组学等 “特征多、样本少” 的场景中，LASSO 几乎是特征筛选的 “标配” 工具。

接下来，我们就通过具体代码，看看如何用 LASSO 在数据中筛选与疾病相关的关键特征。

---

代码流程

• 1.基础工具准备（加载 R 包）

• 2.数据获取与初步观察

• 3.数据格式适配模型要求

• 4.模型构建与初步可视化

• 5.交叉验证优化关键参数

• 6.最终特征提取与结果保存

---

1. 加载分析所需的R包

library(tidyverse)#数据处理与可视化的综合包
library(glmnet)#用于拟合LASSO回归模型
library(e1071)#包含多种机器学习辅助函数

2. 数据准备与初探

这里先看一下我们准备的数据，使用excel的转置功能整理表达矩阵得到

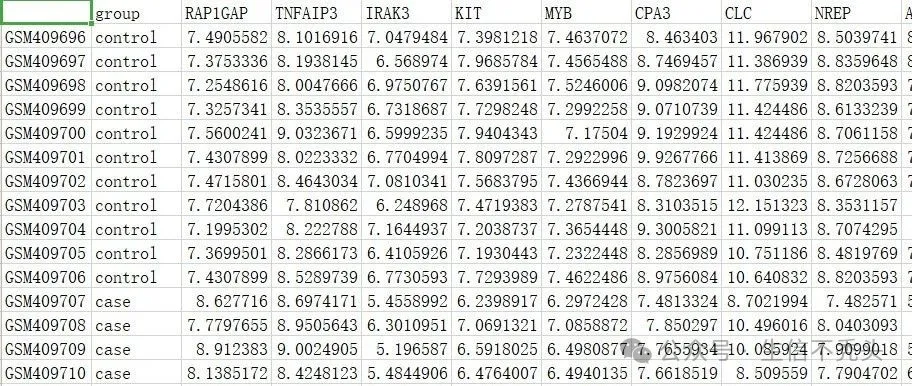
第一列为样本名，第二列为样本信息，后面的所有列为基因表达数据

# 设置工作目录（根据实际情况修改路径）
setwd("D:/文献复现_范科尼贫血/7lasso")

# 读取CSV格式的输入数据
# 参数说明：
# - row.names = 1：将第一列作为行名（通常是样本ID）
# - as.is = FALSE：保持数据原有类型，不自动转换
train <- read.csv("lasso准备数据.csv", row.names = 1, as.is = FALSE)

# 查看数据集基本信息
dim(train)                  # 查看数据集维度（样本数×特征数）
[1]  32 151
train[1:4, 1:4]             # 查看前4行、前4列内容，了解数据格式
            group  RAP1GAP  TNFAIP3    IRAK3
GSM409696 control 7.490558 8.101692 7.047948
GSM409697 control 7.375334 8.193815 6.568974
GSM409698 control 7.254862 8.004767 6.975077
GSM409699 control 7.325734 8.353556 6.731869

这里通过维度可以看到，32行151列，因为包含1列样本信息，所以有32个样本与150个基因。

3. 数据预处理（适配LASSO模型）

# ----------------------------
# 提取特征矩阵（排除第一列分组信息）并转换为矩阵格式
# LASSO模型要求输入的特征必须是矩阵形式
x <- as.matrix(train[, -1])

# 处理因变量：将分组信息（group）转换为二元变量
# control组赋值为0，病例组赋值为1（便于二分类回归分析）
y <- ifelse(train$group == "control", 0, 1)
y                          # 查看转换后的因变量

4. LASSO模型拟合与系数可视化

# 设置随机种子，确保结果可重复
set.seed(1314520)

这里大家一定要养成设置随机种子的习惯。机器学习代码存在一定随机性（后面会提到）。设置随机种子可以确保结果的可重复性。例如从1到10中这10个数字抽取一个数字 两次，只要抽之前设置了相同的随机种子，那两次抽样得到的数字就是相同的。

# 拟合LASSO回归模型
# 参数说明：
# - x：特征矩阵
# - y：二元因变量
# - family = "binomial"：二分类逻辑回归
# - alpha = 1：指定为LASSO回归（alpha=0为Ridge回归）
# - lambda = NULL：让模型自动选择lambda值范围
fit <- glmnet(x, y, family = "binomial", alpha = 1, lambda = NULL)

print(fit)
Call:  glmnet(x = x, y = y, family = "binomial", alpha = 1, lambda = NULL) 

    Df  %Dev  Lambda
1    0  0.00 0.43810
2    2  5.91 0.41820
3    2 11.56 0.39920
4    2 16.69 0.38100

• Df（Degree of Freedom）：当前Lambda下，非零系数的特征数量（即 LASSO 筛选出的 “有效特征数”）。

• %Dev（Percentage of Deviance Explained）：模型解释的偏差百分比。偏差（Deviance）是衡量模型拟合度的指标，%Dev越高，说明模型对 “因变量（如疾病分组）变异” 的解释能力越强。

• Lambda：LASSO 的惩罚参数，λ 越大，惩罚越强（会更严格地压缩系数，甚至将系数逼到 0，减少特征数）；λ 越小，惩罚越弱（系数更难被压缩，特征数易增加，模型拟合度更高）。

# 绘制LASSO回归系数路径图
# 展示不同lambda值下各特征系数的变化趋势
# 参数说明：
# - xvar = "lambda"：x轴为lambda的对数变换值
# - label = TRUE：显示特征标签
plot(fit, xvar = "lambda", label = TRUE)
# 可选：以偏差解释率为x轴的系数路径图
# plot(fit, xvar = "dev", label = TRUE)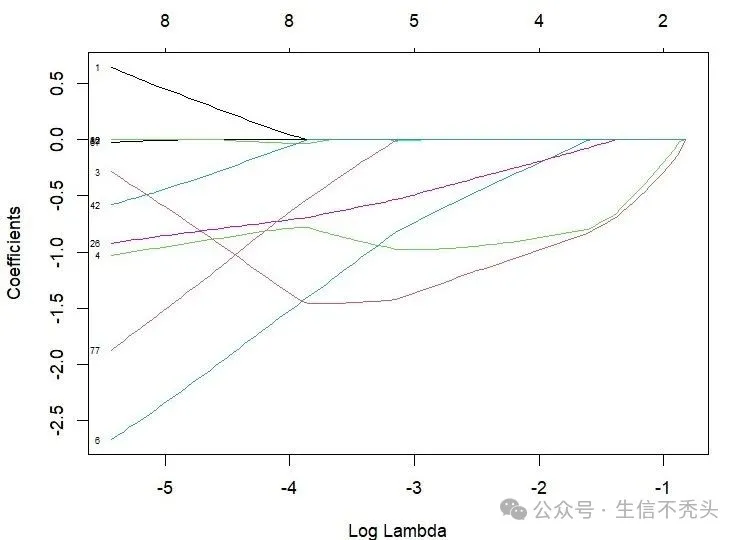

解读：

• 横轴（Log Lambda）：λ 是 LASSO 的惩罚参数，λ 越大（Log Lambda 越靠左，如 - 5 附近），惩罚越强；λ 越小（Log Lambda 越靠右，如 - 1 附近），惩罚越弱。

• 纵轴（Coefficients）：回归系数，表示 “特征与因变量（如疾病分组）的关联强度和方向”（正系数 = 正相关，负系数 = 负相关，绝对值 = 关联强度）。

这张图直观展示了：LASSO 如何通过调整惩罚强度（λ），从 “所有特征” 中逐步筛选出 “与因变量最相关的关键特征”—— 惩罚越强，筛掉的特征越多；惩罚越弱，保留的特征越多，每条彩色曲线代表一个特征（基因）。

5. 交叉验证确定最佳lambda

# 进行10折交叉验证，优化lambda值
#对于该数据来说，可能5倍折叠更好，但按照文献，我们还是选择的10倍折叠
# 参数说明：
# - nfold = 10：10折交叉验证
# - type.measure = 'deviance'：以偏差作为评价指标
cvfit <- cv.glmnet(x, y, nfold = 10, family = "binomial", type.measure = 'deviance')
# 可选：以分类错误率作为评价指标
# cvfit = cv.glmnet(x, y, nfold=10, family = "binomial", type.measure = "class")

这里的nfold折叠数需要特别注意，简单来说nfold指的是将原始数据集分割成的若干个 “子集合”（这里存在随机性）。然后用部分数据训练模型，用另一部分数据验证模型。

为什么要 “分折叠”？

核心是为了 让模型评估更客观。

• 如果不分割折叠，直接用 “全部数据训练，再用全部数据验证”，模型很可能 “记住” 了训练数据的细节（过拟合），导致评估结果虚高（看起来很好，但实际预测新数据时很差）。

• 而 “分折叠” 通过 “训练用大部分数据，验证用小部分新数据”，能更真实地模拟模型在 “未见过的数据” 上的表现，避免过拟合带来的误导。

下方表格仅供大家参考！折叠数还需根据具体样本信息进行选择

样本数	推荐折叠数	核心原因
样本量较小（<50）	5 折	避免验证集过小导致的结果波动，提升评估稳定性
样本量较大（50~200）	10 折	平衡偏差与方差，结果稳定，符合领域惯例

# 绘制交叉验证结果图
# 展示不同lambda值对应的交叉验证误差
# 图中虚线分别表示最小误差点和1个标准差范围内的最佳lambda值
plot(cvfit)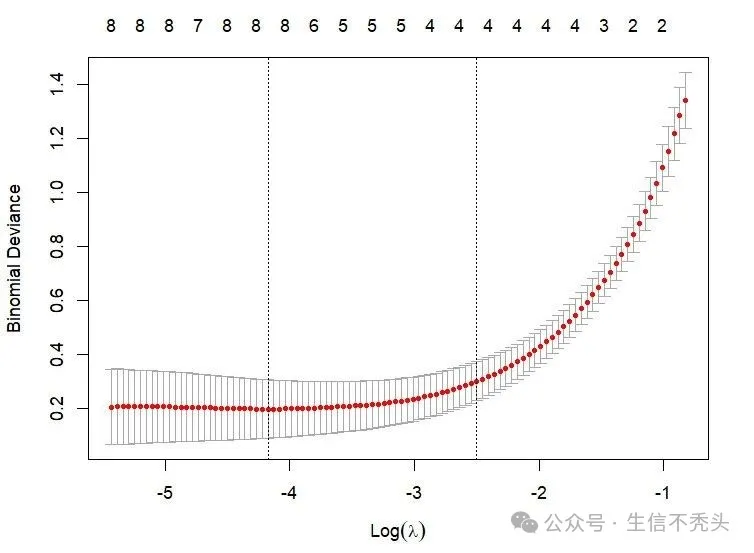

解读：

• 红色点线：不同 λ 对应的交叉验证平均偏差（即 10 折交叉验证后，模型在验证集上的平均误差）。

• 灰色竖线：偏差的标准差（表示 10 次交叉验证中，误差的波动范围）。

• 垂直虚线：通常有两条，对应两个关键 λ：

        左侧虚线：λ.min（使交叉验证偏差最小的 λ，拟合效果最优）。

        右侧虚线：λ.1se（在 λ.min 基础上，偏差增加不超过 1 个标准差的最大 λ，目的是选 “更简洁的模型”—— 惩罚更强，筛选的特征更少）。

• 上方数字：对应 λ 下非零系数的特征数量（即 LASSO 筛选出的 “有效特征数”）。

对于机器学习的结果图确实比较难懂，但论文写作时一般不会要求过多解读

6. 特征筛选与结果保存

# 查看交叉验证得到的最小误差对应的lambda值（最佳lambda）
cvfit$lambda.min
[1] 0.01538247
# 根据最佳lambda值提取模型系数
myCoefs <- coef(cvfit, s = "lambda.min")

如何选最佳 λ？

• 追求 “最佳拟合”：选 λ.min（左侧虚线对应位置）—— 此时模型在验证集上误差最小，但可能保留较多特征。

• 追求 “简约模型”：选 λ.1se（右侧虚线对应位置）—— 此时偏差仅比最小值高 1 个标准差，但惩罚更强，筛选的特征更少（上方数字更小），模型更简洁且泛化能力可能更强。

这里我们选择lambda.min作为最佳λ

lasso_fea <- myCoefs@Dimnames[[1]][which(myCoefs != 0)]
lasso_fea <- lasso_fea[-1]  # 排除第一个截距项（Intercept）

# 展示LASSO回归筛选出的关键特征
lasso_fea
[1] "RAP1GAP" "IRAK3"   "KIT"     "CPA3"    "PRG2"    "HSPA1A"  "IGLL1"   "VNN1"  
# 将筛选得到的特征保存到CSV文件，用于后续分析
write.csv(lasso_fea, "3feature_lasso.csv")

---

至此分析结束，以上内容均为个人学习经验，如有错误，欢迎大家反馈、讨论