这几天百度开源了思考模型ERNIE-4.5-21B-A3B-Thinking，采用混合专家（MoE架构总参数规模达210亿，每个token仅激活30亿参数，在保持高性能的同时大幅降低计算需求。这一技术突破让众多开发者对MoE架构产生了浓厚兴趣。

本文将深入解析MoE架构的核心原理，并提供一份从零开始构建MoEGPT模型的实用指南。

MoE架构概述：稀疏激活的智慧

混合专家模型（也就是MixtureofExperts，简称MoE）它属于一种稀疏激活模型呀。这种模型的核心想法就是运用好多“专家”网络去处理不同领域的任务呢，不过在任何特定的时间里呀，也就只会激活一小部分专家而已。

跟传统的密集模型比起来，MoE模型有这些优势：

• 计算效率高：模型总参数量巨大，但每个输入只激活部分参数，显著降低计算资源需求

• 专家专业化：每个专家网络可以专注于不同领域知识如代码、数学、语言），提升模型在特定任务上的表现

• 扩展性强：通过增加专家数量而非专家深度来扩展模型规模，避免梯度消失和训练困难

# MoE层的基本实现伪代码import torchimport torch.nn as nnimport torch.nn.functional as FclassMoELayer(nn.Module):    def__init__(self, input_dim, output_dim, num_experts):        super(MoELayer, self).__init__()        self.input_dim = input_dim        self.output_dim = output_dim        self.num_experts = num_experts                # 创建专家网络        self.experts = nn.ModuleList([            nn.Linear(input_dim, output_dim) for_in range(num_experts)        ])                # 门控网络（路由器）        self.gate = nn.Linear(input_dim, num_experts)            defforward(self, x):        # 计算门控权重        gate_scores = self.gate(x)        gate_probs = F.softmax(gate_scores, dim=-1)                # 选择top-k专家        topk_probs, topk_indices = torch.topk(gate_probs, k=2, dim=-1)                # 归一化权重        topk_probs = topk_probs / topk_probs.sum(dim=-1, keepdim=True)                # 初始化输出        output = torch.zeros_like(x)                # 计算各专家输出并加权组合        for i in range(self.num_experts):            # 创建当前专家的掩码            expert_mask = (topk_indices == i)            if expert_mask.any():                # 计算当前专家输出                expert_output = self.experts[i](x)                # 应用权重并累加输出                weight = topk_probs * expert_mask.float()                output += expert_output * weight.sum(dim=-1, keepdim=True)                        return output

MoEGPT模型架构设计

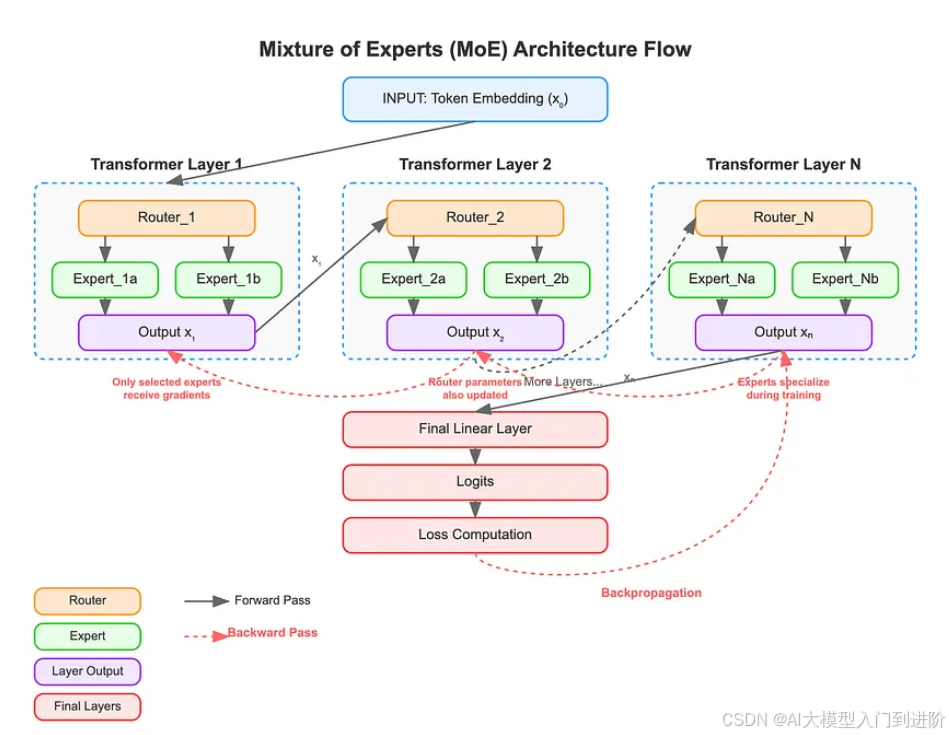
构建一个MoEGPT模型需要在Transformer架构的基础上集成MoE层。关键设计决策包括专家放置策略、门控网络设计和平衡损失。

import mathfrom collections import OrderedDictclassMoETransformerBlock(nn.Module):    def__init__(self, hidden_dim, num_heads, num_experts, expert_capacity, dropout=0.1):        super(MoETransformerBlock, self).__init__()        self.attention = nn.MultiheadAttention(hidden_dim, num_heads, dropout=dropout)        self.norm1 = nn.LayerNorm(hidden_dim)        self.norm2 = nn.LayerNorm(hidden_dim)        self.dropout = nn.Dropout(dropout)                # 用MoE层替代传统的FFN层        self.moe_layer = MoELayer(hidden_dim, hidden_dim * 4, num_experts)        self.expert_capacity = expert_capacity            defforward(self, x, key_padding_mask=None):        # 自注意力子层        attn_output, _ = self.attention(x, x, x, key_padding_mask=key_padding_mask)        x = x + self.dropout(attn_output)        x = self.norm1(x)                # MoE前馈子层        moe_output = self.moe_layer(x)        x = x + self.dropout(moe_output)        x = self.norm2(x)                return x

门控网络在MoE架构里是很关键的部分，它的作用是确定哪些token由哪些专家去处理。现在的MoE实现一般会采用top-k路由策略，这里的k通常是1或者2。

训练策略与挑战应对

MoE模型在训练方面比密集模型要更有难度些，主要得去处理负载不均衡以及训练不稳定这两个问题。

负载平衡与专家利用率

在MoE模型里，保证所有专家都能被充分运用是很关键的。要解决有些专家被过度使用，而另外一些专家被忽略这个问题，就得引入负载平衡损失。

defload_balancing_loss(gate_scores, num_experts, expert_mask):    """    计算负载平衡损失，确保专家利用率均衡    """    # 计算每个专家的使用频率    expert_usage = expert_mask.float().mean(dim=0)        # 计算门控输出的均匀分布    uniform_dist = torch.ones(num_experts, device=gate_scores.device) / num_experts        # 计算KL散度作为负载平衡损失    balance_loss = F.kl_div(        expert_usage.log(),         uniform_dist,         reduction='batchmean'    )        return balance_loss# 在训练循环中defmoe_forward_pass(model, input_ids, labels):    # 前向传播    outputs = model(input_ids)        # 计算标准交叉熵损失    ce_loss = F.cross_entropy(        outputs.logits.view(-1, outputs.logits.size(-1)),        labels.view(-1),        ignore_index=-100    )        # 获取门控分数和专家掩码    gate_scores = outputs.gate_scores    expert_mask = outputs.expert_mask        # 计算负载平衡损失    balance_loss = load_balancing_loss(        gate_scores,         model.num_experts,        expert_mask    )        # 组合损失    total_loss = ce_loss + 0.01 * balance_loss # 平衡损失权重通常较小        return total_loss, ce_loss, balance_loss

梯度裁剪与学习率调度

MoE模型通常需要更精细的超参数调优，

# MoE模型优化器设置示例defget_optimizer(model, learning_rate=1e-4):    # 为不同组件设置不同的学习率    optimizer_params = [        {            'params': model.attention.parameters(),            'lr': learning_rate,            'weight_decay': 0.01        },        {            'params': model.moe_layer.experts.parameters(),            'lr': learning_rate,            'weight_decay': 0.01        },        {            'params': model.moe_layer.gate.parameters(),            'lr': learning_rate * 10, # 门控网络通常使用更高学习率            'weight_decay': 0.0        }    ]        optimizer = torch.optim.AdamW(optimizer_params)    return optimizer# 学习率调度defget_scheduler(optimizer, warmup_steps, total_steps):    deflr_lambda(current_step):        if current_step < warmup_steps:            return float(current_step) / float(max(1, warmup_steps))        else:            progress = float(current_step - warmup_steps) / float(max(1, total_steps - warmup_steps))            return max(0.0, 0.5 * (1.0 + math.cos(math.pi * progress)))        return torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda)

推理优化与部署策略

MoE模型在进行推理这个阶段的时候呢，得进行特殊的优化，这样才能把它高效地部署起来。其中关键的技术包含了动态负载平衡、专家并行以及缓存优化这几个方面。

KV缓存优化

由于MoE模型的稀疏特性，KeyValue缓存需要特殊处理：

classMoEKVCache:    def__init__(self, max_batch_size, max_seq_length, hidden_size, num_experts):        self.cache = {}        self.max_batch_size = max_batch_size        self.max_seq_length = max_seq_length        self.hidden_size = hidden_size        self.num_experts = num_experts            defupdate(self, batch_idx, expert_idx, token_idx, key, value):        # 初始化缓存如果不存在        if (batch_idx, expert_idx) notinself.cache:            self.cache[(batch_idx, expert_idx)] = {                'keys': torch.zeros(self.max_seq_length, self.hidden_size),                'values': torch.zeros(self.max_seq_length, self.hidden_size),                'count': 0            }                # 更新缓存        cache_entry = self.cache[(batch_idx, expert_idx)]        cache_entry['keys'][token_idx] = key        cache_entry['values'][token_idx] = value        cache_entry['count'] += 1            defget(self, batch_idx, expert_idx, token_indices):        if (batch_idx, expert_idx) notinself.cache:            return None, None                    cache_entry = self.cache[(batch_idx, expert_idx)]        keys = cache_entry['keys'][token_indices]        values = cache_entry['values'][token_indices]                return keys, values

模型分片与专家并行

为了高效部署大型MoE模型，需要将专家分布across multiple devices：

# 专家并行部署示例class ExpertParallel(nn.Module):    def __init__(self, experts, device_list):        super(ExpertParallel, self).__init__()        self.device_list = device_list        self.num_devices = len(device_list)                # 将专家分布到不同设备上        self.experts_per_device = len(experts) // self.num_devices        self.expert_devices = []                for i, expert in enumerate(experts):            device_idx = i % self.num_devices            device = self.device_list[device_idx]            expert.to(device)            self.expert_devices.append(device)                def forward(self, x, expert_indices):        # 根据专家索引路由到不同设备        outputs = []        for i, expert_idx in enumerate(expert_indices):            device = self.expert_devices[expert_idx]            x_i = x[i].to(device)            expert = self.experts[expert_idx]            output = expert(x_i.unsqueeze(0))            outputs.append(output.cpu())                    return torch.cat(outputs, dim=0)

实际应用场景与性能分析

MoE模型在好多不同的场景里都展现得很厉害，尤其在计算资源不是很多，但又需要去处理各种各样任务的时候。

案例研究：代码生成与补全

在代码生成这个活儿里，不同的专家能把精力放在不一样的编程语言上，或者不一样类型的代码结构方面（像函数啦、类啦、文档字符串之类的）。

# MoE代码生成模型示例classMoECodeModel(nn.Module):    def__init__(self, vocab_size, hidden_dim, num_heads, num_experts, num_layers):        super(MoECodeModel, self).__init__()        self.token_embedding = nn.Embedding(vocab_size, hidden_dim)        self.position_embedding = nn.Embedding(1024, hidden_dim)                # 使用MoE Transformer层        self.layers = nn.ModuleList([            MoETransformerBlock(hidden_dim, num_heads, num_experts, expert_capacity=512)            for_in range(num_layers)        ])                self.output_layer = nn.Linear(hidden_dim, vocab_size)            defforward(self, input_ids):        batch_size, seq_len = input_ids.shape                # 创建位置索引        positions = torch.arange(seq_len, device=input_ids.device).unsqueeze(0).expand(batch_size, seq_len)                # 计算嵌入        token_embeds = self.token_embedding(input_ids)        position_embeds = self.position_embedding(positions)        x = token_embeds + position_embeds                # 通过所有层        for layer inself.layers:            x = layer(x)                    # 输出投影        logits = self.output_layer(x)                return logits

性能对比分析

根据百度开源ERNIE-4.5-21B-A3B-Thinking的数据，MoE模型在多项基准测试中表现出色：

1. 效率提升：相比密集模型，推理速度提升约1.3倍
2. 资源节约：激活参数减少约85%（仅激活30亿参数，总参数210亿）
3. 性能保持：在逻辑推理、数学、科学等任务上保持接近SOTA的性能

未来发展与技术演进

MoE技术仍在快速发展中，以下几个方向值得关注：

动态专家选择

以后的MoE模型或许能依据输入的复杂程度，随时对激活专家的数量进行调整，从而让计算效率得到更进一步的优化。

# 动态专家选择示例classDynamicMoELayer(nn.Module):    def__init__(self, input_dim, output_dim, num_experts, min_experts=1, max_experts=4):        super(DynamicMoELayer, self).__init__()        self.input_dim = input_dim        self.output_dim = output_dim        self.num_experts = num_experts        self.min_experts = min_experts        self.max_experts = max_experts                self.experts = nn.ModuleList([nn.Linear(input_dim, output_dim) for_in range(num_experts)])        self.gate = nn.Linear(input_dim, num_experts + 1) # 额外输出用于决定专家数量            defforward(self, x):        # 预测门控分数和所需专家数量        gate_output = self.gate(x.mean(dim=1)) # 全局平均池化        expert_scores = gate_output[:, :-1]        num_experts_pred = torch.sigmoid(gate_output[:, -1]) * (self.max_experts - self.min_experts) + self.min_experts        num_experts = torch.round(num_experts_pred).int()                # 选择top-k专家，k为动态决定        gate_probs = F.softmax(expert_scores, dim=-1)        topk_probs, topk_indices = torch.topk(gate_probs, k=self.max_experts, dim=-1)                # 动态调整实际使用的专家数量        output = torch.zeros_like(x)        for i in range(x.size(0)):            k = min(num_experts[i].item(), self.max_experts)            for j in range(k):                expert_idx = topk_indices[i, j]                expert_output = self.experts[expert_idx](x[i].unsqueeze(0))                weight = topk_probs[i, j]                output[i] += expert_output.squeeze(0) * weight                        return output

多模态MoE模型

MoE架构天然适合多模态任务，不同专家可以处理不同模态的信息：

# 多模态MoE示例class MultimodalMoE(nn.Module):    def __init__(self, text_dim, image_dim, audio_dim, hidden_dim, num_experts):        super(MultimodalMoE, self).__init__()                # 模态特定的投影层        self.text_proj = nn.Linear(text_dim, hidden_dim)        self.image_proj = nn.Linear(image_dim, hidden_dim)        self.audio_proj = nn.Linear(audio_dim, hidden_dim)                # 模态专家        self.text_experts = nn.ModuleList([nn.Linear(hidden_dim, hidden_dim) for _ in range(num_experts//3)])        self.image_experts = nn.ModuleList([nn.Linear(hidden_dim, hidden_dim) for _ in range(num_experts//3)])        self.audio_experts = nn.ModuleList([nn.Linear(hidden_dim, hidden_dim) for _ in range(num_experts//3)])                # 跨模态门控        self.cross_modal_gate = nn.Linear(hidden_dim * 3, num_experts)            def forward(self, text_x, image_x, audio_x):        # 投影到共同空间        text_h = self.text_proj(text_x)        image_h = self.image_proj(image_x)        audio_h = self.audio_proj(audio_x)                # 融合多模态信息        combined = torch.cat([text_h.mean(dim=1), image_h.mean(dim=1), audio_h.mean(dim=1)], dim=1)                # 计算门控分数        gate_scores = self.cross_modal_gate(combined)        gate_probs = F.softmax(gate_scores, dim=-1)                # 选择专家并计算输出        # ... 简化实现                return combined_output

总结：MoE技术的价值与挑战

MoE架构为大规模语言模型提供了一条高效的扩展路径，让资源有限的开发者和组织也能训练和使用超大规模模型。大家可能也注意到了，今年发布的开源/闭源的大模型大部分都是MoE架构的。

核心优势

1. 计算效率：通过稀疏激活大幅降低计算和内存需求
2. 专业方面的能力：各个专家能够把精力集中在不一样的领域或者任务上
3. 可扩展性：通过增加专家数量而非深度来扩展模型能力
4. 灵活性：支持动态架构调整，适应不同计算预算

实践建议

1. 从小开始：从24个专家的简单MoE模型开始，逐步增加复杂度
2. 留意负载情况：要时刻关注专家的使用效率，一定得让负载达到平衡状态。
3. 调整超参数：MoE模型通常需要不同的学习率和梯度裁剪策略
4. 硬件规划：考虑专家并行所需的额外通信开销

未来展望

随着像百度ERNIE-4.5-21B-A3B-Thinking这样的开源MoE模型的出现，以及GPT-OSS模型，MoE技术有望进一步大规模访问和使用。

以后MoE的发展有可能会聚焦在动态选择专家、不同模式进行整合以及效率更高的路由算法等方面。对开发者和组织来讲，当下投入精力去学习和尝试MoE技术，能给未来的AI应用开发打下稳固的根基。

普通人如何抓住AI大模型的风口？

领取方式在文末

为什么要学习大模型？

目前AI大模型的技术岗位与能力培养随着人工智能技术的迅速发展和应用 ， 大模型作为其中的重要组成部分 ， 正逐渐成为推动人工智能发展的重要引擎 。大模型以其强大的数据处理和模式识别能力， 广泛应用于自然语言处理 、计算机视觉 、 智能推荐等领域 ，为各行各业带来了革命性的改变和机遇 。

目前，开源人工智能大模型已应用于医疗、政务、法律、汽车、娱乐、金融、互联网、教育、制造业、企业服务等多个场景，其中，应用于金融、企业服务、制造业和法律领域的大模型在本次调研中占比超过 30%。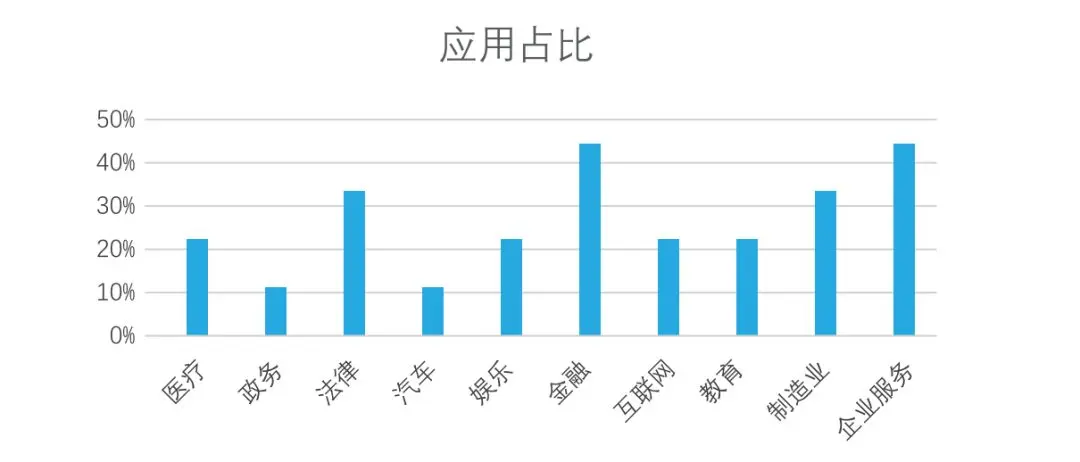

随着AI大模型技术的迅速发展，相关岗位的需求也日益增加。大模型产业链催生了一批高薪新职业：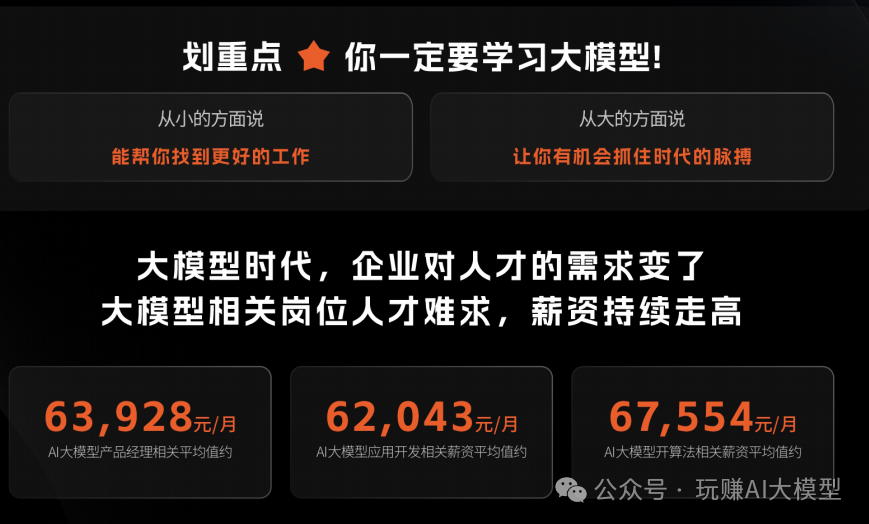

人工智能大潮已来，不加入就可能被淘汰。如果你是技术人，尤其是互联网从业者，现在就开始学习AI大模型技术，真的是给你的人生一个重要建议！

最后

只要你真心想学习AI大模型技术，这份精心整理的学习资料我愿意无偿分享给你，但是想学技术去乱搞的人别来找我！

在当前这个人工智能高速发展的时代，AI大模型正在深刻改变各行各业。我国对高水平AI人才的需求也日益增长，真正懂技术、能落地的人才依旧紧缺。我也希望通过这份资料，能够帮助更多有志于AI领域的朋友入门并深入学习。

真诚无偿分享！！！
vx扫描下方二维码即可
加上后会一个个给大家发

大模型全套学习资料展示

自我们与MoPaaS魔泊云合作以来，我们不断打磨课程体系与技术内容，在细节上精益求精，同时在技术层面也新增了许多前沿且实用的内容，力求为大家带来更系统、更实战、更落地的大模型学习体验。

希望这份系统、实用的大模型学习路径，能够帮助你从零入门，进阶到实战，真正掌握AI时代的核心技能！

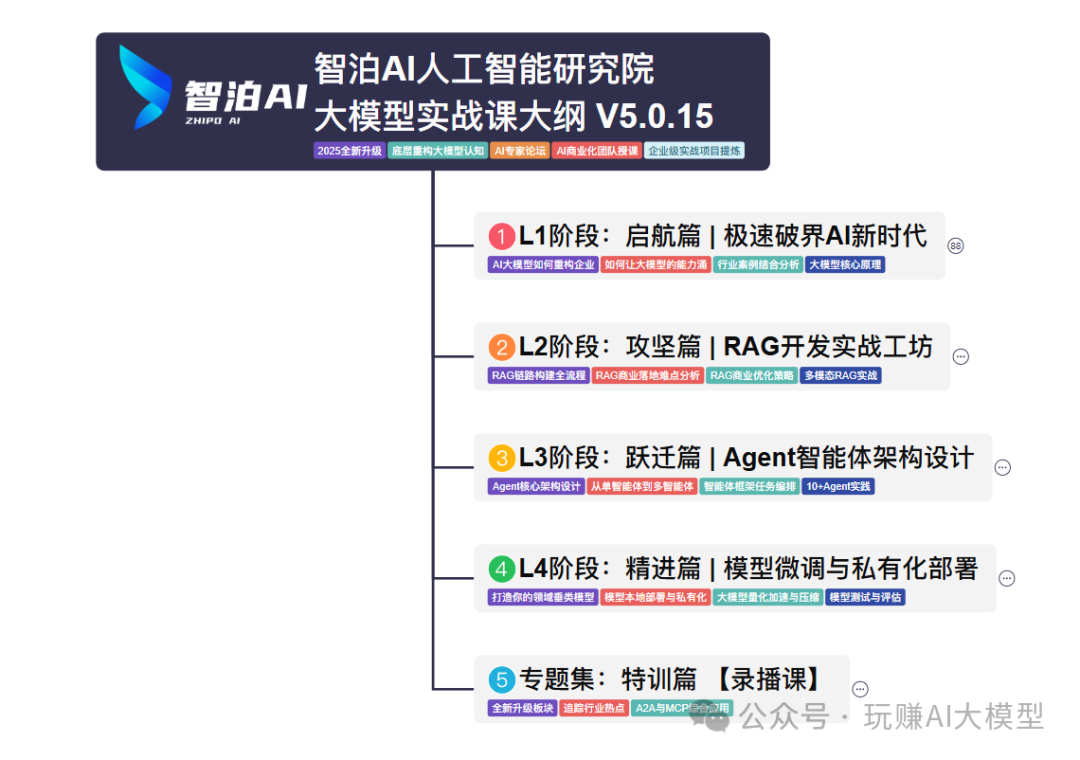
01 教学内容

• 从零到精通完整闭环：【基础理论 →RAG开发 → Agent设计 → 模型微调与私有化部署调→热门技术】5大模块，内容比传统教材更贴近企业实战！

• 大量真实项目案例： 带你亲自上手搞数据清洗、模型调优这些硬核操作，把课本知识变成真本事‌！

02适学人群

应届毕业生‌： 无工作经验但想要系统学习AI大模型技术，期待通过实战项目掌握核心技术。

零基础转型‌： 非技术背景但关注AI应用场景，计划通过低代码工具实现“AI+行业”跨界‌。

业务赋能突破瓶颈： 传统开发者（Java/前端等）学习Transformer架构与LangChain框架，向AI全栈工程师转型‌。

vx扫描下方二维码即可

本教程比较珍贵，仅限大家自行学习，不要传播！更严禁商用！

03 入门到进阶学习路线图

大模型学习路线图，整体分为5个大的阶段：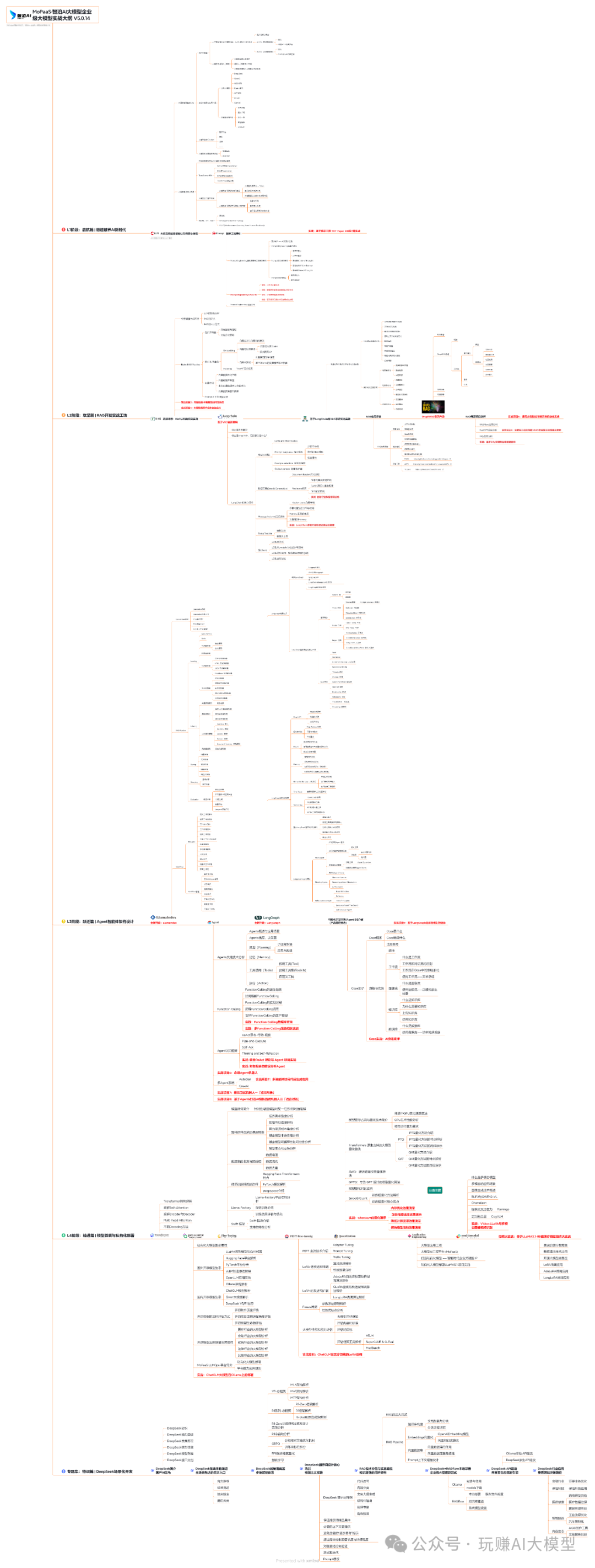

04 视频和书籍PDF合集

从0到掌握主流大模型技术视频教程（涵盖模型训练、微调、RAG、LangChain、Agent开发等实战方向）

新手必备的大模型学习PDF书单来了！全是硬核知识，帮你少走弯路（不吹牛，真有用）

05 行业报告+白皮书合集

收集70+报告与白皮书，了解行业最新动态！

06 90+份面试题/经验

AI大模型岗位面试经验总结（谁学技术不是为了赚$呢，找个好的岗位很重要）

07 deepseek部署包+技巧大全

由于篇幅有限

只展示部分资料

并且还在持续更新中…

真诚无偿分享！！！
vx扫描下方二维码即可
加上后会一个个给大家发