线性代数和数据挖掘(一):线性代数

人工智能中线性代数的相关内容

Mrliu__

582人浏览 · 2025-09-29 09:00:00

Mrliu__ · 2025-09-29 09:00:00 发布

文章目录

前言

线性代数作为数学的重要分支，是计算机科学、机器学习、图形学等领域的基础工具。无论是数据降维、图像变换还是AI模型训练，都离不开向量、矩阵等核心概念的支撑。本文将系统梳理线性代数核心知识，拆解重难点，并结合Python代码实现实战，帮你真正掌握这门"工科数学语言"。本篇主要是阐述基本知识,方便之后的Numpy数组的学习

一、思维导图

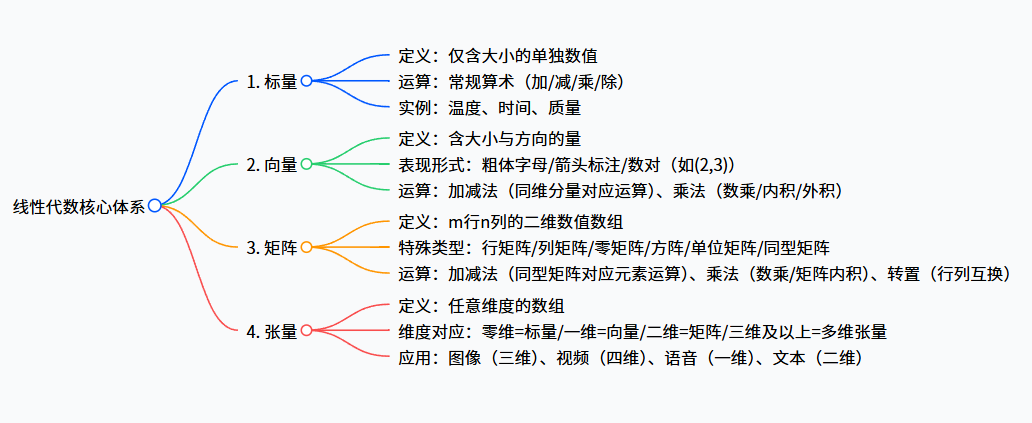
请添加图片描述

二、核心概念与运算详解

2.1 标量

标量是最简单的数学对象，仅包含大小，无方向属性，本质是一个单独的数，可分为整数、实数或复数。

在数学计算中，标量支持常规的算术运算，例如两个标量3和5，可进行3+5=8的加法运算、5-3=2的减法运算、3×5=15的乘法运算以及5÷3≈1.67的除法运算，运算规则与基础数学一致。

2.2 向量

2.2.1 表现形式

向量同时具备大小与方向，几何上可形象化为带箭头的线段——箭头指向代表方向，线段长度代表大小。数学表示中，向量常用粗体字母（如 $\vec{a}$ ）或字母加箭头（如 $\vec{a}$ ）标注，在空间直角坐标系中，还可表示为有序数对，例如平面直角坐标系中的(2,3)就是一个二维向量，三维空间中的(1,2,3)则是三维向量。

2.2.2 向量加减法

向量加减法有严格的前提条件：参与运算的向量必须是同维向量，即拥有相同数量的分量（如二维向量只能与二维向量运算，三维向量只能与三维向量运算）。

运算规则为"对应分量相加减"：对于向量 $\vec{a}=(a_{1}, a_{2}, ..., a_{n})$ 和 $\vec{b}=(b_{1}, b_{2}, ..., b_{n})$ ，它们的和为 $\vec{a}+\vec{b}=(a_{1}+b_{1}, a_{2}+b_{2}, ..., a_{n}+b_{n})$ ，差为 $\vec{a}-\vec{b}=(a_{1}-b_{1}, a_{2}-b_{2}, ..., a_{n}-b_{n})$ 。

实例：在平面直角坐标系中，若 $\overrightarrow{AB}=(1,2)$ 、 $\overrightarrow{AC}=(3,2)$ ，则 $\overrightarrow{AB}+\overrightarrow{AC}=(1+3,2+2)=(4,4)$ （对应向量 $\overrightarrow{AD}$ ）， $\overrightarrow{AB}-\overrightarrow{AC}=(1-3,2-2)=(-2,0)$ （对应向量 $\overrightarrow{AE}$ ）。

2.2.3 向量乘法

向量乘法分为三大类，具体规则与应用场景各不相同：

数乘（标量×向量）
本质是改变向量的大小与方向：用标量k乘以向量 $\vec{a}$ ，向量的每个分量都乘以k。若k为正数，向量方向不变，大小变为原来的k倍；若k为负数，向量方向反转，大小变为原来的|k|倍。
实例： $\vec{a}=(1,1)$ ，数乘2后得到(2,2)，数乘-2后得到(-2,-2)。
内积（点积，向量×向量）
运算结果为标量，公式为"对应分量乘积之和"：对于 $\vec{a}=(x_1,y_1)$ 和 $\vec{b}=(x_2,y_2)$ ，内积 $\vec{a}·\vec{b}=x_1x_2+y_1y_2$ 。
实例： $\vec{a}=(2,3)$ ， $\vec{b}=(4,-1)$ ，则 $\vec{a}·\vec{b}=2×4+3×(-1)=8-3=5$ 。
延伸应用：可通过内积计算两向量夹角，公式为 $\cos\theta=\frac{\vec{a}·\vec{b}}{|\vec{a}||\vec{b}|}$ （其中 $|\vec{a}|$ 、 $|\vec{b}|$ 分别为两向量的模长）。
外积（叉积，向量×向量）
仅对三维向量有定义，运算结果为新向量：新向量方向垂直于原两向量组成的平面，大小等于原两向量组成平行四边形的面积。
计算规则：对于三维向量 $\vec{A}=(A_{x}, A_{y}, A_{z})$ 和 $\vec{B}=(B_{x}, B_{y}, B_{z})$ ，外积 $\vec{A}×\vec{B}$ 通过行列式计算：
$\vec{A} × \vec{B}=\left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ A_{x} & A_{y} & A_{z} \\ B_{x} & B_{y} & B_{z}\end{array}\right|$
实例： $\vec{a}=(2,3,0)$ ， $\vec{b}=(4,-1,0)$ ，外积结果为 $(3 \times 0 - 0 \times (- 1), 0 \times 4 - 2 \times 0, 2 \times (- 1) - 3 \times 4) = (0, 0, - 14)$ 。

2.3 矩阵

2.3.1 基本定义

矩阵是由数字组成的二维数组，常用大写字母表示（如A），维度由行数m和列数n确定（记为m×n矩阵）。其数学表达式为：
$A=\left(\begin{array}{llll} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdot \cdot & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m 1} & a_{m 2} & \cdots & a_{m n} \end{array}\right)$
其中 $a_{ij}$ 代表矩阵A的第i行第j列元素，矩阵的每一行可视为行向量，每一列可视为列向量。

2.3.2 特殊类型矩阵

不同场景下，矩阵有多种特殊形式，核心类型如下：

类型	定义	示例（数学表达式）
行矩阵	仅1行的矩阵（行向量）	$\left[\begin{array}{lllll}a_{1} & a_{2} & a_{3} & \cdots & a_{n}\end{array}\right]$
列矩阵	仅1列的矩阵（列向量）	$\begin{bmatrix} a_{1} \\ a_{2} \\ \vdots \\ a_{n} \end{bmatrix}$
零矩阵	所有元素均为0的矩阵	$\left[\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right]$
方阵	行数=列数的矩阵（n阶方阵）	$\left[\begin{array}{lll}1 & 2 & 3 \\ 1 & 2 & 3 \\ 1 & 2 & 3\end{array}\right]$
单位矩阵	主对角线元素为1，其余为0的方阵	$\left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]$
同型矩阵	行数、列数分别相等的矩阵	A(3×3)与B(3×3)（如A= $\left[\begin{array}{lll}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{array}\right]$ ，B= $\left[\begin{array}{lll}9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1\end{array}\right]$ ）

2.3.3 矩阵运算

加减法
前提条件：参与运算的矩阵必须是同型矩阵（行数、列数分别相等）。
运算规则：对应位置元素相加减，结果仍为同型矩阵。
实例：矩阵A= $\left[\begin{array}{lll}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{array}\right]$ ，矩阵B= $\left[\begin{array}{lll}9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1\end{array}\right]$ ，则A+B= $\left[\begin{array}{lll}1+9 & 2+8 & 3+7 \\ 4+6 & 5+5 & 6+4 \\ 7+3 & 8+2 & 9+1\end{array}\right]=\left[\begin{array}{lll}10 & 10 & 10 \\ 10 & 10 & 10 \\ 10 & 10 & 10\end{array}\right]$ 。
乘法
矩阵乘法分为"数乘"和"矩阵内积"两类：
- 数乘（常数×矩阵）：将矩阵的所有元素乘以常数k，相当于对矩阵进行"缩放"。
  实例：矩阵A= $\left[\begin{array}{lll}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{array}\right]$ ，与常数2数乘后，结果为 $\left[\begin{array}{ccc}2 & 4 & 6 \\ 8 & 10 & 12 \\ 14 & 16 & 18\end{array}\right]$ 。
- 矩阵内积（矩阵×矩阵）：前提条件是第一个矩阵的列数=第二个矩阵的行数，结果矩阵的行数=第一个矩阵的行数，列数=第二个矩阵的列数（记为 $A_{m×n}×B_{n×p}=C_{m×p}$ ）。
  运算规则：结果矩阵C的第i行第j列元素 $c_{ij}$ ，等于A的第i行与B的第j列对应元素乘积之和。
  实例：A= $\left[\begin{array}{l}9 \\ 6 \\ 3\end{array}\right]$ （3×1矩阵），B= $\left[\begin{array}{lll}1 & 2 & 3\end{array}\right]$ （1×3矩阵），则A×B= $\left[\begin{array}{ccc}9×1 & 9×2 & 9×3 \\ 6×1 & 6×2 & 6×3 \\ 3×1 & 3×2 & 3×3\end{array}\right]=\left[\begin{array}{ccc}9 & 18 & 27 \\ 6 & 12 & 18 \\ 3 & 6 & 9\end{array}\right]$ 。
  注意：矩阵内积不满足交换律，即A×B≠B×A，甚至可能出现A×B可运算但B×A不可运算的情况。
转置
定义：将矩阵的行与列互换，得到的新矩阵称为原矩阵的转置矩阵（记为 $A^T$ ）。若原矩阵为m×n矩阵，转置后变为n×m矩阵。
实例：矩阵A= $\left[\begin{array}{ll}1 & 2 \\ 3 & 4 \\ 5 & 6\end{array}\right]$ （3×2矩阵），转置后为 $\left[\begin{array}{lll}1 & 3 & 5 \\ 2 & 4 & 6\end{array}\right]$ （2×3矩阵）。

2.4 张量：超越二维的"多维数组"

张量是标量、向量、矩阵的推广，可表示任意维度的数组：

零维张量：即标量（单独的数）；
一维张量：即向量（有序数值列表）；
二维张量：即矩阵（二维数值阵列）；
三维及以上张量：如三维张量可表示RGB彩色图像（维度为"高度×宽度×颜色通道"），四维张量可表示视频（维度为"时间×高度×宽度×颜色通道"）。

在人工智能领域，张量是核心数据载体，应用场景包括：

数据表示：图像（三维）、视频（四维）、语音（一维，每个元素为时间点音频样本）、文本（二维，每行代表一个单词的向量）；
参数存储：神经网络的权重、偏置以张量形式保存；
运算支撑：卷积神经网络的卷积操作、全连接层的矩阵乘法，均基于张量运算实现；
并行计算：张量运算适配GPU并行架构，是深度学习模型高效训练的基础。

三、重难点与常见误区解析

3.1 向量运算的核心误区

误区1：不同维度的向量可以进行加减法。
纠正：向量加减法要求"同维"，例如二维向量(1,2)不能与三维向量(1,2,3)运算，否则会因分量数量不匹配导致结果无意义。
误区2：向量内积与外积混淆。
纠正：内积结果是标量，适用于计算夹角、投影等场景；外积仅对三维向量定义，结果是向量，适用于计算垂直方向、面积等场景，二者运算规则与应用场景完全不同。

3.2 矩阵乘法的关键注意事项

运算前提：必须满足"前矩阵列数=后矩阵行数"，例如2×3矩阵只能与3×4矩阵相乘，不能与2×4矩阵相乘。
交换律问题：矩阵乘法不满足交换律，例如A×B和B×A的结果可能不同，甚至其中一个不可运算（如A为2×3矩阵，B为3×2矩阵，A×B为2×2矩阵，B×A为3×3矩阵，结果维度不同）。
与元素乘法的区别：矩阵内积是"行×列"运算，而元素乘法（Hadamard积）是对应位置元素相乘，二者逻辑完全不同，需根据需求选择正确运算方式。