🏆 本文收录于 《YOLOv8实战：从入门到深度优化》，该专栏持续复现网络上各种热门内容(全网YOLO改进最全最新的专栏，质量分97分+，全网顶流)，改进内容支持(分类、检测、分割、追踪、关键点、OBB检测)。且专栏会随订阅人数上升而涨价(毕竟不断更新)，当前性价比极高，有一定的参考&学习价值，部分内容会基于现有的国内外顶尖人工智能AIGC等AI大模型技术总结改进而来，嘎嘎硬核。
  
✨ 特惠福利：目前活动一折秒杀价！一次订阅，永久免费，所有后续更新内容均免费阅读！

全文目录：

⏩ 摘要

大家好，欢迎来到《YOLOv8专栏》卷积创新篇的第26节！在本节中，我们将探索一种完全不同于传统空间域卷积的强大技术——傅里叶卷积 (Fourier Convolution)。传统的CNN卷积核通过在局部邻域内滑动来提取特征，感受野的增长需要堆叠大量层级，这对于捕获全局上下文信息构成了挑战。傅里叶卷积借助神奇的傅里叶变换，将图像从空间域转换到频域，通过在频域中进行简单的元素乘法，一步到位实现全局感受野的建模。这种独特的机制为处理长距离依赖、检测大目标以及理解复杂场景提供了全新的视角。本文将带您从傅里叶变换的基础理论出发，深入剖析其如何在神经网络中实现卷积操作，分析其计算复杂度，并最终探讨如何将其与YOLOv8结合，为您的检测模型注入来自频域的强大动力。准备好进入频域的世界，开启一场颠覆性的认知之旅吧！🎉

⏩ 上期回顾：Capsule Network胶囊卷积网络

  在上一节**《YOLOv8【卷积创新篇·第25节】Capsule Network胶囊卷积网络》** 中，我们一同探索了由Geoffrey Hinton提出的革命性概念——胶囊网络（Capsule Network）。我们了解到，传统CNN中的池化操作虽然增强了特征的不变性（invariance），但也丢失了宝贵的空间位置和姿态信息。

  胶囊网络通过将神经元“升级”为“胶囊”，用向量或矩阵来表示特征，从而能够同时编码特征的存在概率和姿态属性。其核心的动态路由算法，使得网络能够智能地识别出部分与整体之间的层次关系，实现了更强大的等变性（equivariance）。这意味着，当目标发生旋转、缩放或视角变化时，胶ax囊网络能够更好地理解这些变换，而不是简单地忽略它们。

  我们探讨了胶囊网络的基本概念、动态路由的实现细节，并分析了其在目标检测中保留目标精确空间关系的潜力。然而，我们也认识到，胶囊网络复杂的动态路由机制带来了巨大的计算开销，使其在追求极致速度的YOLOv8这类实时检测器中的应用仍然面临挑战。

  正是因为这些挑战，我们继续探索其他能够高效捕获全局信息的替代方案。如果说胶囊网络是通过复杂的路由机制来理解“空间关系”，那么我们今天要介绍的傅里叶卷积，则是通过“频率分解”这一优雅的数学工具，从另一个维度——频域，来瞬间把握全局！让我们看看这条路是否能走得更远、更高效！🚀

⏩ 正文

⏩ 1. 魔法的数学工具：快速傅里叶变换 (FFT)

  在深入傅里叶卷积之前，我们必须先掌握它的核心技术——傅里叶变换（Fourier Transform）。别担心，我们不会陷入复杂的数学公式推导，而是通过直观的例子和代码来理解它。

1.1 什么是傅里叶变换？从声音到图像

  想象一下，你听到了一段优美的音乐，比如一段和弦。在时域（Time Domain）里，你听到的是一个随时间变化的复杂声波。但你的大脑和耳朵很神奇，能分辨出这个和弦是由哪些音符（比如Do, Mi, Sol）组成的。

  傅里叶变换做的就是类似的事情。它是一种数学工具，能将一个复杂的信号（如声波）分解成一系列简单的正弦波和余弦波。每个简单的波都有自己的频率和振幅。

  能将一个复杂的信号（如声波）分解成一系列简单的正弦波和余弦波。每个简单的波都有自己的频率和振幅。

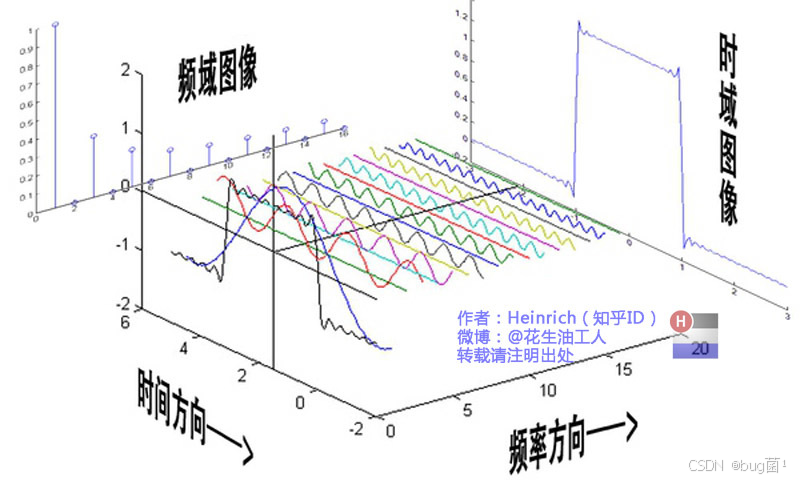
  这个概念同样适用于二维的图像。我们可以把图像看作一个二维信号。一张图像中，变化缓慢的区域（如大片的天空、平滑的墙壁）对应着低频信号，而变化剧烈的区域（如物体的边缘、复杂的纹理）则对应着高频信号。

  傅里叶变换能将一张图像从我们熟悉的空间域（Spatial Domain），转换到一个全新的维度——频域（Frequency Domain）。在频域中，我们不再看到像素的位置，而是看到组成这张图像的所有频率成分的分布。

1.2 频域的秘密：幅度和相位

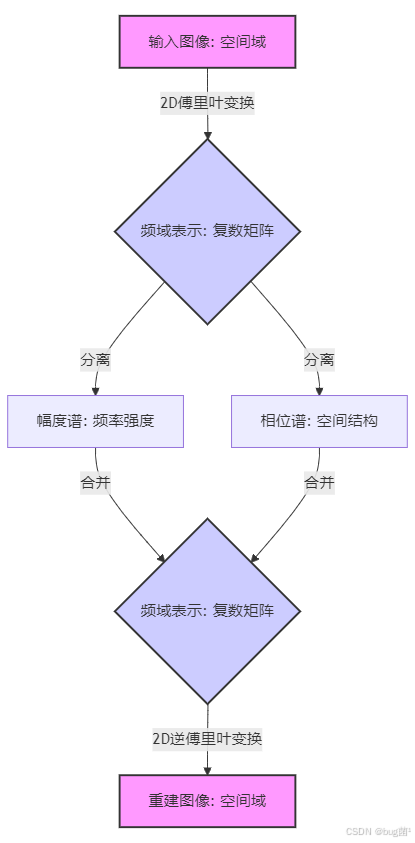
  对图像进行二维傅里叶变换（2D-FFT）后，我们会得到一个复数矩阵。这个矩阵包含了两个关键信息：

  1. 幅度谱（Magnitude Spectrum）: 描述了每个频率分量的“强度”或“能量”。通常，图像的幅度谱中心点是低频区域，越往外频率越高。大部分自然图像的能量都集中在低频区域，所以幅度谱的中心会非常亮。
  2. 相位谱（Phase Spectrum）: 描述了每个频率分量的“位置”或“相位”。相位谱包含了物体结构和位置的关键信息，虽然看起来像随机噪声，但它对图像重建至关重要。

  我们可以用下面的图来形象地表示这个过程：

1.3 为什么选择“快速”傅里叶变换 (FFT)？

  标准的离散傅里叶变换（DFT）计算量非常大，对于一个 N x N 的图像，其时间复杂度为 O ( N 4 ) O(N^4) O(N4)。这在深度学习中是完全无法接受的。

  而快速傅里叶变换（Fast Fourier Transform, FFT） 是一种高效的算法，用于计算DFT。它通过“分治法”的思想，将时间复杂度大大降低到了 O ( N 2 log ⁡ N ) O(N^2 \log N) O(N2logN)。正是因为FFT的存在，才使得在神经网络中利用傅里叶变换成为可能。

1.4 PyTorch实战：图像的频域之旅

  光说不练假把式！让我们用PyTorch来看看图像在频域里到底长什么样。

import torch
import torch.fft as fft
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
import requests

# --- 准备一张示例图片 ---
# 我们从网络加载一张图片用于演示
url = 'https://upload.wikimedia.org/wikipedia/commons/thumb/1/1a/Cheetah_in_the_Serengeti_in_Tanzania-2.jpg/1280px-Cheetah_in_the_Serengeti_in_Tanzania-2.jpg'
try:
    img = Image.open(requests.get(url, stream=True).raw).convert('L') # 转换为灰度图
    img = img.resize((256, 256)) # 调整大小方便显示
except Exception as e:
    print(f"无法加载图片，请检查网络连接或URL: {e}")
    # 创建一个备用图片
    img_np = np.zeros((256, 256))
    img_np[100:156, 100:156] = 255 # 中间创建一个白色方块
    img = Image.fromarray(img_np.astype(np.uint8))

img_np = np.array(img)
img_tensor = torch.from_numpy(img_np).float()

# --- 执行2D-FFT ---
# torch.fft.fft2 会对最后两个维度进行FFT
freq_tensor = fft.fft2(img_tensor)

# --- 为了可视化，将零频点（低频）移动到中心 ---
# fftshift将(0,0)处的直流分量移到频谱中心
shifted_freq_tensor = fft.fftshift(freq_tensor)

# --- 计算幅度谱和相位谱 ---
# 幅度谱: 通常取对数使其可视化效果更好
magnitude_spectrum = torch.log(torch.abs(shifted_freq_tensor) + 1e-8)
# 相位谱
phase_spectrum = torch.angle(shifted_freq_tensor)

# --- 将频域图像逆变换回空间域 ---
# 首先将频谱中心移回左上角
inv_shifted_freq_tensor = fft.ifftshift(shifted_freq_tensor)
# 执行逆FFT
reconstructed_img_tensor = fft.ifft2(inv_shifted_freq_tensor)
# 取实部，因为原始图像是实数，虚部理论上应接近于0
reconstructed_img_tensor = torch.real(reconstructed_img_tensor)

# --- 可视化结果 ---
plt.figure(figsize=(15, 10))
plt.subplot(2, 3, 1)
plt.imshow(img_np, cmap='gray')
plt.title('Original Image')
plt.axis('off')

plt.subplot(2, 3, 2)
plt.imshow(magnitude_spectrum.numpy(), cmap='gray')
plt.title('Magnitude Spectrum (log scale)')
plt.axis('off')

plt.subplot(2, 3, 3)
plt.imshow(phase_spectrum.numpy(), cmap='gray')
plt.title('Phase Spectrum')
plt.axis('off')

plt.subplot(2, 3, 5)
plt.imshow(reconstructed_img_tensor.numpy(), cmap='gray')
plt.title('Reconstructed Image')
plt.axis('off')

plt.tight_layout()
plt.show()

代码解析:

  1. 图像: 我们加载一张图片并将其转换为灰度图张量。
  2. fft.fft2(img_tensor): 这是核心函数，对输入的2D张量执行FFT，输出一个同样大小的复数张量。
  3. fft.fftshift.): FFT的标准输出会将低频成分放在四个角上，这不便于观察。fftshift函数将低频成分移动到图像中心，这样中心是最低频，四周是最高频，符合人类直觉。
  4. 计算谱: 我们使用torch.abs计算幅度，torch.angle计算相位。对幅度取对数torch.log`是为了压缩动态范围，让暗淡的高频细节也能被看见。
  5. 逆变换: fft.ifft2是逆变换函数。注意在逆变换之前，需要用fft.ifftshift将频谱移回原来的位置。最后用torch.real取实部得到重建的图像。

  从运行结果中你会惊奇地发现，重建的图像与原图几乎一模一样，证明了傅里叶变换是可逆的。同时，观察幅度谱，你会看到中心区域非常亮，这印证了“自然图像能量主要集中在低频”的观点。

⏩ 2.域卷积：全新的卷积实现范式

  理解了FFT后，我们终于可以揭开傅里叶卷积的神秘面纱了。它的理论基础是一个非常优美的数学定理。

2.1 核心基石：卷积定理

卷积定理（Convolution Theorem） 指出：

两个函数在 空间域 的卷积，等价于它们各自进行傅里叶变换后，在 频域 的 逐元素乘积（Element-wise Product）。

用公式表达就是：

f ( x ) ∗ g ( x ) = F − 1 { F { f ( x ) } ⋅ F { g ( x ) } } f(x) * g(x) = \mathcal{F}^{-1}\left\{ \mathcal{F}\{f(x)\} \cdot \mathcal{F}\{g(x)\} \right\} f(x)∗g(x)=F−1{F{f(x)}⋅F{g(x)}}

  其中 * 代表卷积操作，· 代表逐元素乘积， F \mathcal{F} F 代表傅里叶变换， F − 1 \mathcal{F}^{-1} F−1 代表逆傅里叶变换。

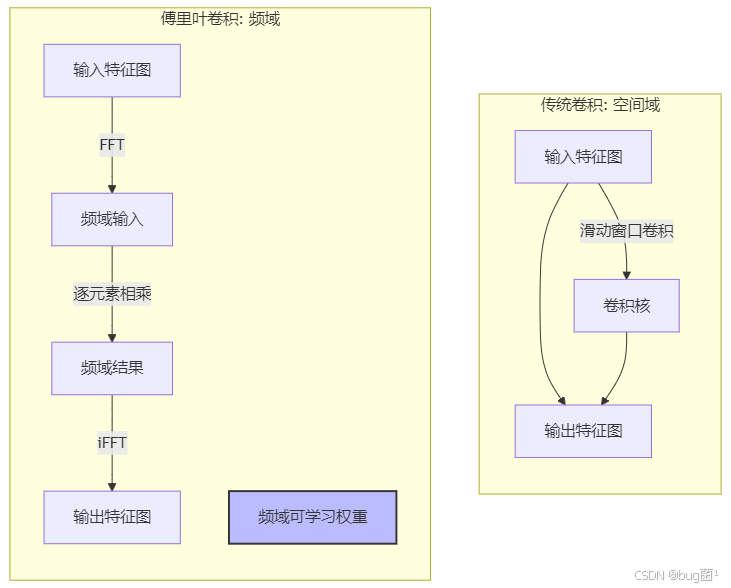
  这个定理简直是为我们量身定做的！传统的卷积操作需要在空间域上进行复杂的滑动、相乘、再求和。
而现在，我们可以将输入和卷积核都变换到频域，然后只需要做一次简单的矩阵乘法，再把结果变换回空间域即可！

  这为我们设计神经网络层提供了一个全新的思路 🚀，并附上相关演示图：

2.2 构建一个傅里叶卷积层

  基于卷积定理，一个傅里叶卷积层的工作流程如下：

  1. 输入: 接收一个空间域的输入特征图 x（尺寸为 [B, C, H, W]）。
  2. 变换域: 对 x 的最后两个维度（H, W）执行2D-FFT，得到频域表示 x_freq。
  3. 定义可学习权重: 在频域中定义一个可学习的权重张量 W_freq。这个权重张量的大小与 x_freq 的频域尺寸相匹配。这就是我们的“卷积核”，只不过它存在于频域中。
  4. 变换回空间域: 对相乘后的结果执行逆2D-FFT（iFFT），得到最终的空间域输出特征图。

  一个关键点是，为了处理多通道（channel）图像，我们需要像标准卷积一样，为输入和输出的每个通道组合定义权重。

2.3 PyTorch实战：FourierConv2d模块的实现

现在，我们将上述流程封装成一个PyTorch的nn.Module，让它可以像nn.Conv2d一样即插即用。

import torch
import torch.nn as nn
import torch.fft as fft

class FourierConv2d(nn.Module):
    """
    一个2D傅里叶卷积层实现
    """
    def __init__(self, in_channels, out_channels, height, width):
        """
        初始化函数
        :param in_channels: 输入通道数
        :param out_channels: 输出通道数
        :param height: 输入特征图的高度
        :param width: 输入特征图的宽度
        """
        super(FourierConv2d, self).__init__()
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.height = height
        self.width = width
        
        # 频域中的可学习权重
        # 频率分量的数量是 width // 2 + 1 (因为傅里叶变换对于实数输入是共轭对称的)
        # 我们需要为每个输入输出通道对学习一个权重矩阵
        # 权重是复数，所以我们用一个额外的维度(2)来表示实部和虚部
        self.weights = nn.Parameter(
            torch.randn(in_channels, out_channels, self.height, self.width // 2 + 1, 2)
        )
        self.weights.data.normal_(mean=0, std=0.02) # 使用较小的标准差进行初始化

    def forward(self, x):
        """
        前向传播函数
        :param x: 输入张量, 形状为 (B, C_in, H, W)
        :return: 输出张量, 形状为 (B, C_out, H, W)
        """
        B, C, H, W = x.shape
        
        # 检查输入尺寸是否与初始化时一致
        if H != self.height or W != self.width:
            raise ValueError(f"Input image size ({H},{W}) doesn't match layer's expected size ({self.height},{self.width})")
            
        # 1. 对输入进行2D-FFT
        # torch.fft.rfft2 对于实数输入更高效，它只返回非冗余的频率分量
        x_freq = fft.rfft2(x, s=(self.height, self.width), norm='ortho')
        # x_freq 的形状: (B, C_in, H, W//2 + 1)，复数形式
        
        # 2. 将我们的权重转换为复数形式
        # torch.view_as_complex 将最后一个维度为2的实数张量视为复数张量
        weights_complex = torch.view_as_complex(self.weights)
        
        # 3. 在频域进行逐元素乘法
        # 为了进行矩阵乘法般的通道混合，我们需要调整维度
        # (B, C_in, H, W//2+1) @ (C_in, C_out, H, W//2+1) -> (B, C_out, H, W//2+1)
        # 我们使用 einsum 来实现这个复杂的批次化矩阵乘法
        # 'bixy,ioxy->boxy' 表示：
        # b: batch, i: in_channels, o: out_channels, x: height, y: width_freq
        out_freq = torch.einsum('bixy,ioxy->boxy', x_freq, weights_complex)
        
        # 4. 进行逆FFT回到空间域
        # 使用 irfft2 因为我们的原始输入是实数
        x_out = fft.irfft2(out_freq, s=(self.height, self.width), norm='ortho')
        
        return x_out

# --- 使用示例 ---
# 假设我们有一个batch=4, channels=3, size=64x64的输入
input_tensor = torch.randn(4, 3, 64, 64)

# 创建一个傅里叶卷积层，输出16个通道
fourier_conv_layer = FourierConv2d(in_channels=33, out_channels=16, height=64, width=64)

# 执行前向传播
output_tensor = fourier_convlayer(input_tensor)

print("输入张量形状:", input_tensor.shape)
print("输出张量形状:", output_tensor.shape)

代码解析:

  1. __init__:

    • 与普通卷积层不同，傅里叶卷积层需要预先知道输入特征图的高和宽，因为频域权重的大小与此直接相关。
      self.weights: 这是本层的核心。我们定义的权重直接存在于频域。注意尺寸 (..., self.width / 2 + 1 2)。width / 2 + 1 是因为对于实数输入，其傅里叶变换是共轭对称的，torch.fft.rfft2这个优化函数只会计算并返回非冗余的一半频率，从而节省计算和存储。最后的2 用于分别存储复数的实部和虚部。

  2. forward:

    • fft.rfft2(x, normrtho'): 对输入 x 执行FFT。norm='ortho' 是一个好习惯，它能确保变换和逆变换在数值上更稳定，保持信号的能量不变。
    • torch.view_as_complex(self.weights): 将我们存储为实数对的权重“看作”Pytorch原生的复数类型，这样才能与FFT的输出进行复数运算。
      torch.einsum(...): 这是最关键的一步。简单的逐元素乘法只能实现深度可分离卷积（Depthwise Convolution）的效果，即每个输入通道的特征只影响对应的输出通道。为了实现标准卷积那样的通道间信息交互，我们需要一个类似矩阵乘法的操作。einsum (Einstein summation) 是一个极其强大的工具，'bixy,ioxy->boxy' 这条规则精确地描述了我们想要的操作：对于每一个批次(b)和每一个频域位置(x,y)，我们都用输入通道(i)的特征向量与一个 (C_in, C_out) 的权重矩阵相乘，得到输出通道(o)的特征向量。fft.irfft2(...): 将计算结果从频域变换回空间域，得到最终的输出。

现在，我们拥有了一个功能完整的 FourierConv2d 层，可以嵌入到任何神经网络中了！

⏩ 3. 全局感受野：一眼看尽全局的奥秘

  傅里叶卷积最令人兴奋的特性，就是它天生的全局感受野（Global Receptive Field）。

3.1 频域操作的全局性

  回顾一下傅里叶变换的定义，一个信号在频域中的每一个点的值，都是由其在时域/空间域中所有点的值加权求和得到的。反之，逆变换时，空间域中的每一个像素*的值，也依赖于频域中的所有频率分量**。

  这意味着什么？

当我们在频域中改变任何一个权重值时，这个改变会通过逆傅里叶变换，影响到输出特征图上的每一个像素点！

  这就是全局感受野的本质。傅里叶卷积层不像传统卷积那样需要一个一个像素地“爬行”来慢慢扩大感受野，它只需要一次变换，就能“看”到整个输入图像。

3.2 与传统卷积感受野的对比

  让我们用一个图来直观对比一下：

Fourier Convolution Network
Legend_F
Standard CNN
Legend
FFT
Input Image
Multiply by Freq Weights
iFFT
Single Pixel Output
Global from the start
Receptive Field
3x3 Conv
Input
3x3 Conv
3x3 Conv
Pixel
Grows layer by layer
Receptive Field
  • 传统CNN: 一个像素点的感受野是有限的，它的大小取决于卷积核大小和网络深度。要获得全局感受野，要么需要非常深的网络，要么需要引入特殊的模块，如池化、空洞卷积或注意力机制。
  • 傅里叶卷积: 仅需一层，输出的任何一个像素都包含了输入图像所有像素的信息。
3.3 全模的优势与应用场景

拥有全局感受野带来了许多潜在优势：

  1. 高效处理长距离依赖: 对于需要理解图像中相距很远的两个物体之间关系的任务（例如，场景理解），傅里叶卷积能直接建立这种联系。
  2. 更检测大目标: 对于占据图像大部分区域的大目标，全局感受野能一次性捕捉其完整轮廓和内部纹理，而不需要多层卷积来拼凑。
  3. 替代注意力机制: 自注意力机制（Self-Attention）是另一种实现全局感受野的流行方法，但其计算复杂度是像素数的平方（ O ( N 2 ) O(N^2) O(N2)）。傅里叶卷积提供了一种计算上更高效的替代方案。

⏩ 4. 性能大比拼：计算复杂度分析

  一个新模块是否实用，很大程度上取决于它的计算效率。

4.1 傅里叶卷积的计算开销

  我们来分解一下FourierConv2d前向传播的计算量（假设输入为 B, C_in, H, W，输出为 B, C_out, H, W）：

  1. FF: rfft2 的复杂度约为 O ( B ⋅ C i n ⋅ H W log ⁡ ( H W ) ) O(B \cdot C_{in} \cdot HW \log(HW)) O(B⋅Cin​⋅HWlog(HW))。
  2. 频法: einsum 操作的复杂度为 O ( B ⋅ C i n ⋅ C o u t ⋅ H W ) O(B \cdot C_{in} \cdot C_{out} \cdot HW) O(B⋅Cin​⋅Cout​⋅HW)。
  3. iFFT: irfft2 的复杂度与FFT类似，约为 O ( B ⋅ C o u t ⋅ H W log ⁡ ( H W ) ) O(B \cdot C_{out} \cdot HW \log(HW)) O(B⋅Cout​⋅HWlog(HW))。

  总的来说，其复杂度可以近似为 O ( B ⋅ H W ⋅ ( C i n log ⁡ ( H W ) + C i n C o u t + C o u t log ⁡ ( H W ) ) ) O(B \cdot HW \cdot (C_{in} \log(HW) + C_{in}C_{out} + C_{out} \log(HW))) O(B⋅HW⋅(Cin​log(HW)+Cin​Cout​+Cout​log(HW)))。

4.2标准卷积的效率对决

  标准2D卷积（nn.Conv2d）的计算复杂度为 O ( B ⋅ C i n ⋅ C o u t ⋅ K 2 ⋅ H W ) O(B \cdot C_{in} \cdot C_{out} \cdot K^2 \cdot HW) O(B⋅Cin​⋅Cout​⋅K2⋅HW)，其中 K 是卷积核大小。

让我们来一场对决：

特性 标准卷积 (Conv2d) 傅里叶卷积 (FourierConv2d)
计算复杂度 O ( K 2 ⋅ C i n C o u t ⋅ H W ) O(K^2 \cdot C_{in}C_{out} \cdot HW) O(K2⋅Cin​Cout​⋅HW) O ( H W ⋅ C i n C o u t + … log ⁡ ( H W ) ) O(HW \cdot C_{in}C_{out} + \dots \log(HW)) O(HW⋅Cin​Cout​+…log(HW))
对卷积核大小 K 敏感，K越大，计算量平方级增长 不敏感，与空间核大小无关
**对图像尺寸 H, W 线性增长 几乎是线性对数增长 ( N log ⁡ N N \log N NlogN)
全局感受野 需要堆叠多层 天生具备
参数量 C i n ⋅ C o u t ⋅ K 2 C_{in} \cdot C_{out} \cdot K^2 Cin​⋅Cout​⋅K2 C i n ⋅ C o u t ⋅ H ⋅ ( W / 2 + 1 ) C_{in} \cdot C_{out} \cdot H \cdot (W/2+1) Cin​⋅Cout​⋅H⋅(W/2+1)

结论:

    • 当卷积核 K 较小（如3x3, 5x5）时，标准卷积通常更快。

  • 当需要非常大的感受野，即等效的 K 变得很大时，傅里叶卷积的 O ( N log ⁡ N ) O(N \log N) O(NlogN) 优势开始显现，会比大核卷积（Large Kernel Convolution）更有效率。

  • 一个需要特别注意的问题是量。标准的傅里叶卷积参数量与特征图大小有关，这可能导致参数爆炸。因此，需要优化策略。

4.3件支持与实际性能考量

  现代GPU（尤其是NVIDIA的Tensor Cores）对标准卷积有极深的优化（如im2col, Winograd算法）。而FFT虽然也有高效的cuFFT库支持，但在通用深度学习框架中的集成和优化程度可能不如标准卷积。因此，理论上的复杂度优势不一定能完全转化为实际的运行速度优势。在部署时需要进行实际的性能剖析（profiling）。

⏩ 5. 优化与YOLOv8集成：从理论到实践

  直接使用我们上面实现的FourierConv2d可能会因为参数过多的问题而效果不佳。学术界已经提出了一些优化方案。

5.1 通过频域滤波优化参数

  一个非常重要的观察是：大部分自然图像的有用信息都集中在低频区域。高频信息通常与噪声和精细的纹理有关。

  因此，我们可以不必为整个频域的所有频率都分配可学习的权重。我们可以只在中心低频区域保留可学习的参数，而将高频区域的权重直接置为零。

  这种思想源于著名的傅里叶神经算子（Fourier Neural Operator, FNO）。

  让我们来修改一下我们的FourierConv2d层，只保留一部分频率模式进行学习。

class FNOConv2d(nn.Module):
    """
    一个更高效的2D傅里叶卷积层，只在低频部分进行学习
    灵感来源于 Fourier Neural Operator
    """
    def __init__(self, in_channels, out_channels, modes):
        """
        :param in_channels: 输入通道数
        :param out_channels: 输出通道数
        :param modes: 在每个维度上保留的傅里叶模式数量(低频分量的数量)
        """
        super(FNOConv2d, self).__init__()
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.modes1 = modes # 对应高度
        self.modes2 = modes # 对应宽度

        # 我们只创建需要学习的低频部分的权重
        self.weights1 = nn.Parameter(
            torch.randn(in_channels, out_channels, self.modes1, self.modes2, 2)
        )
        self.weights1.data.normal_(mean=0, std=0.02)
        self.weights2 = nn.Parameter(
            torch.randn(in_channels, out_channels, self.modes1, self.modes2, 2)
        )
        self.weights2.data.normal_(mean=0, std=0.02)

    def forward(self, x):
        B, C, H, W = x.shape
        
        # 1. FFT
        x_freq = fft.rfft2(x, norm='ortho')
        
        # 创建一个全零的输出频域张量
        out_freq = torch.zeros(B, self.out_channels, H, W // 2 + 1, device=x.device, dtype=torch.cfloat)
        
        # 2. 将可学习权重应用到低频区域
        weights1_complex = torch.view_as_complex(self.weights1)
        weights2_complex = torch.view_as_complex(self.weights2)
        
        # 右上角的低频区域
        out_freq[:, :, :self.modes1, :self.modes2] = torch.einsum(
            "bixy,ioxy->boxy", 
            x_freq[:, :, :self.modes1, :self.modes2], 
            weights1_complex
        )
        # 左下角的低频区域（由于共轭对称性）
        out_freq[:, :, -self.modes1:, :self.modes2] = torch.einsum(
            "bixy,ioxy->boxy", 
            x_freq[:, :, -self.modes1:, :self.modes2], 
            weights2_complex
        )

        # 3. iFFT
        x_out = fft.irfft2(out_freq, s=(H, W), norm='ortho')
        
        return x_out

# --- 使用示例 ---
# 假设 modes=16, 远小于 H,W=64
fno_conv_layer = FNOConv2d(in_channels=3, out_channels=16, modes=16)
output_tensor_fno = fno_conv_layer(input_tensor)
print("\n--- FNO Conv ---")
print("输入张量形状:", input_tensor.shape)
print("输出张量形状:", output_tensor_fno.shape)

代码解析:

  • modes: 这个新参数控制我们保留多少低频模式。modes=16 意味着我们只在中心的 16x1 区域内学习权重。

  • 参数量: 参数量现在只与 modes 有关，而与输入图像的 `H, W 无关！这极大地减少了参数数量，使得模型更轻量，也更不容易过拟合。

  • 频域操作: 我们只对 x_freq 的左上角和右下角的低频部分应用可学习的权重，其他高频部分则被“截断”（即乘以0），这起到了一种低通滤波的作用。

5.2 YOLOv8集成思路：替换或增强

将傅里叶卷积集成到YOLOv8中，有几种有趣的思路：

  1. 替换SPPF (Spatial Pyramid Pooling - Fast): YOLOv8的颈部（Neck）使用SPPF模块通过不同大小的池化来获得多尺度感受野。我们可以用一个傅里-叶卷积层（如FNOConv2d）来替换它。SPPF的目的是捕获上下文信息，而傅里叶卷积的全局感受野天然就能做到这一点，甚至可能做得更好。
  2. 构建混合模块 (C2f-Fourier): 在C2f模块中，通常由多个Bottleneck组成。我们可以设计一个新的Bottleneck，将其中的一个3x3 Conv`替换为傅里叶卷积层。这样，C2f模块就能同时拥有传统卷积的局部特征提取能力和傅里叶卷积的全局上下文感知能力。
  3. 作为最后的全局处理层: 在整个Backbone或Neck的末端，添加一个傅里叶卷积层，用于对最高层的语义特征进行全局信息融合，然后再送入检测头（Head）。

推荐思路: 构建混合模块。这种方式最为灵活，因为它保留了CNN强大的局部特征提取能力（这对于检测小目标至关重要），同时又引入了全局信息，是一种优势互补的策略。

5.3 集成代码示例与解析

  我们来尝试实现一个C2fFourier模块。首先，我们需要定义一个FourierBottleneck。

# 假设这是YOLOv8模型定义文件的一部分（如 ultralytics/nn/modules.py）
# 需要先将我们上面定义的 FNOConv2d 类放在这个文件里

class FourierBottleneck(nn.Module):
    """一个将标准卷积和傅里叶卷积结合的Bottleneck"""
    def __init__(self, c1, c2, shortcut=True, g=1, e=0.5, modes=16):
        super().__init__()
        c_ = int(c2 * e)  # hidden channels
        self.cv1 = nn.Conv2d(c1, 2 * c_, 1, 1, bias=False)
        self.bn1 = nn.BatchNorm2d(2 * c_)
        self.act = nn.SiLU()
        # 这里用FNOConv2d替换了原来的3x3卷积
        self.fno_conv = FNOConv2d(c_, c_, modes=modes) 
        self.bn2 = nn.BatchNorm2d(c_)
        self.cv2 = nn.Conv2d(c_, c2, 1, 1, bias=False)
        self.bn3 = nn.BatchNorm2d(c2)
        self.add = shortcut and c1 == c2

    def forward(self, x):
        # 保存残差连接的输入
        y = x if self.add else x
        
        # 1x1 卷积扩展通道
        x = self.act(self.bn1(self.cv1(x)))
        
        # 分割成两部分
        x1, x2 = x.chunk(2, 1)
        
        # 一路进行傅里叶卷积
        x1_fno = self.act(self.bn2(self.fno_conv(x1)))
        
        # 另一路可能保持不变或也进行处理（这里简化，直接与Fno结果拼接）
        # 在一个完整的C2f中，x2会被送入下一个bottleneck
        # 这里我们假设这是bottleneck内部的处理
        
        # 1x1 卷积压缩通道
        # 为了演示，我们先将两路合并
        # 注意：在真实的C2f中，结构会更复杂，这里仅为示意
        # 此处简化为一个类似ResBlock的结构
        out = self.bn3(self.cv2(x1_fno)) # 只用了fno这一路来简化演示
        
        return y + out if self.add else out

# --- 如何在YOLOv8的YAML配置文件中调用 ---
# 假设你把 C2fFourier 模块也定义好了，它会使用上面的 FourierBottleneck
# 你可以在你的 my_yolo.yaml 中这样写：

# backbone:
#   # [from, number, module, args]
#   - [-1, 1, Conv, [64, 3, 2]]  # 0-P1/2
#   - [-1, 1, Conv, [128, 3, 2]] # 1-P2/4
#   - [-1, 3, C2f, [128, True]]
#   - [-1, 1, Conv, [256, 3, 2]] # 3-P3/8
#   - [-1, 6, C2f, [256, True]]
#   - [-1, 1, Conv, [512, 3, 2]] # 5-P4/16
#   # 在这里，我们将最后一个C2f替换为C2fFourier
#   - [-1, 3, C2fFourier, [512, True, 16]] # 假设最后一个参数是modes

集成解析:

  1. 定义FourierBottleneck: 我们创建了一个新的瓶颈层，它内部用FNOConv2d代替了原来的nn.Conv2d(c_, c_, 3, 1, 1)。这使得这个模块具备了全局全局信息处理能力。modes`参数可以作为一个超参数进行调节。
  2. 定义C2fFourier (未完全展示): 你仿照YOLOv8中C2f的实现，创建一个C2fFourier模块，让它在其内部循环调用FourierBottleneck而不是标准的Bottleneck。
  3. 修改YAML文件: 最优雅的集成方式是通过修改模型的.yaml配置文件。你需要将新的模块名（如C2fFourier）注册到YOLOv8的解析器中，然后在yaml文件里像使用C2f一样使用它。这样可以无需大幅改动核心代码，保持了YOLOv8框架的灵活性。

实验建议:

  • 从替换高层特征开始。在网络的深层，特征图尺寸较小，语义信息更丰富，此时引入全局感受野的收益最大。
  • 调节modes参数。modes是一个重要的超参数，它控制了模型的容量和对低频信息的关注度。modes越大，参数越多，模型表达能力越强，但可能过拟合；modes越小，模型越轻量，但可能丢失细节。
  • 对比实验。在你的数据集上，严格对比原始YOLOv8和集成了傅里叶卷积的YOLOv8在mAP、参数量、GFLOPs和推理速度上的差异，用数据说话。

⏩ 6.结与展望

  本节课，我们进行了一场从空间域到频域的奇妙旅行。我们深入探讨了傅里叶卷积的原理、实现与应用。

核心知识点回顾:

  • 傅里叶变换(FFT): 将图像从空间域分解到频域，揭示其频率构成。
  • 卷积定理: 空间域的卷积等价于频域的逐元素乘积，是傅里叶卷积的理论基石。
  • 全局感受野: 傅里叶卷积通过一次操作即可捕获整个特征图的信息，擅长处理长距离依赖。
  • 效率与权衡: 相比于大核卷积，傅里叶卷积在计算上更高效，但参数量可能成为瓶颈，需要通过低频滤波等策略（如FNO）进行优化。
  • YOLOv8集成: 傅里叶卷积可以作为一种强大的即插即用模块，用于替换或增强YOLOv8中的现有结构（如SPPF或C2f），以提升模型的全局上下文理解能力。

  傅里叶卷积为我们打开了一扇新的大门，让我们认识到卷积操作并非只有在空间域滑动这一种形式。它与近来热门的注意力机制、Transformer等都属于探索如何高效建模全局信息的前沿方向。虽然它也有自身的局限性（如对平移等变换不如标准卷积具有等变性），但其独特的视角和高效的全局建模能力，使其在未来的模型设计中必将占有一席之地。

  希望通过今天的学习，你能对频域处理有一个全新的认识，并激发你动手实验，将这些酷炫的技术应用到自己的YOLOv8模型中去的想法！动手试试吧，也许下一个SOTA模型就出自你手！🎉

⏩ 下期预告：Sparse Convolution稀疏卷积优化

  在今天的探索中，我们关注的是如何“看得更远”，实现全局感受野。然而，在许多现实场景中，我们面临的另一个巨大挑战是数据的稀疏性。

  想象一下自动驾驶中的激光雷达点云，或者医疗影像中的细胞切片，亦或是高分辨率图像中的小目标。在这些场景中，有用的信息往往只占据了整个数据空间的一小部分，大部分区域都是空白或不重要的背景。对这些“空”的地方使用标准的密集卷积（Dense Convolution）无疑是巨大的计算浪费。

  下一节，《YOLOv8【卷积创新篇·第27节】Sparse Convolution稀疏卷积优化》，我们将把目光聚焦于如何“看得更精”，学习一种为稀疏数据量身定做的卷积方式——稀疏卷积。我们将揭示其如何只在有数据的地方进行计算，从而在处理点云、高分辨率图像等任务时，大幅提升模型的计算效率和内存效率。敬请期待！✨✨✨

  希望本文所提供的YOLOv8内容能够帮助到你，特别是在模型精度提升和推理速度优化方面。

  PS：如果你在按照本文提供的方法进行YOLOv8优化后，依然遇到问题，请不要急躁或抱怨！YOLOv8作为一个高度复杂的目标检测框架，其优化过程涉及硬件、数据集、训练参数等多方面因素。如果你在应用过程中遇到新的Bug或未解决的问题，欢迎将其粘贴到评论区，我们可以一起分析、探讨解决方案。如果你有新的优化思路，也欢迎分享给大家，互相学习，共同进步！

🧧🧧 文末福利，等你来拿！🧧🧧

  文中讨论的技术问题大部分来源于我在YOLOv8项目开发中的亲身经历，也有部分来自网络及读者提供的案例。如果文中内容涉及版权问题，请及时告知，我会立即修改或删除。同时，部分解答思路和步骤来自全网社区及人工智能问答平台，若未能帮助到你，还请谅解！YOLOv8模型的优化过程复杂多变，遇到不同的环境、数据集或任务时，解决方案也各不相同。如果你有更优的解决方案，欢迎在评论区分享，撰写教程与方案，帮助更多开发者提升YOLOv8应用的精度与效率！

  OK，以上就是我这期关于YOLOv8优化的解决方案，如果你还想深入了解更多YOLOv8相关的优化策略与技巧，欢迎查看我专门收集YOLOv8及其他目标检测技术的专栏《YOLOv8实战：从入门到深度优化》。希望我的分享能帮你解决在YOLOv8应用中的难题，提升你的技术水平。下期再见！

  码字不易，如果这篇文章对你有所帮助，帮忙给我来个一键三连（关注、点赞、收藏），你的支持是我持续创作的最大动力。

  同时也推荐大家关注我的公众号：「猿圈奇妙屋」，第一时间获取更多YOLOv8优化内容及技术资源，包括目标检测相关的最新优化方案、BAT大厂面试题、技术书籍、工具等，期待与你一起学习，共同进步！

🫵 Who am I?

我是bug菌，CSDN | 掘金 | InfoQ | 51CTO | 华为云 | 阿里云 | 腾讯云 等社区博客专家，C站博客之星Top30，华为云多年度十佳博主，掘金多年度人气作者Top40，掘金等各大社区平台签约作者，51CTO年度博主Top12，掘金/InfoQ/51CTO等社区优质创作者；全网粉丝合计 30w+；更多精彩福利点击这里；硬核微信公众号「猿圈奇妙屋」，欢迎你的加入！免费白嫖最新BAT互联网公司面试真题、4000G PDF电子书籍、简历模板等海量资料，你想要的我都有，关键是你不来拿。

-End-

# 计算机视觉
Logo
北京朝阳AI社区

更多推荐

cover

[AI工作流搭建笔记](3)基于cursor+MCP+python:企业定制知识库

avatar 北京朝阳AI社区
cover

Python+TypeScript打造AI应用，MCP服务器让大模型获取上下文

avatar 北京朝阳AI社区
cover

AI技术圈最新技术速览【2025年9月】

avatar 北京朝阳AI社区