💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文内容如下：🎁🎁🎁

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

带阻尼的PID控制器在多智能体系统单个智能体控制中的应用研究

摘要

本文聚焦于带阻尼的PID控制器在多智能体系统中单个智能体控制的应用研究。通过引入微分项（D项）的阻尼作用，结合比例（P项）和积分（I项）环节，构建适用于多智能体动态环境的PID控制框架。研究结果表明，带阻尼的PID控制器能有效提升单个智能体的轨迹跟踪精度、抗干扰能力和系统稳定性，尤其在存在通信延迟或模型不确定性的场景下表现突出。

1. 引言

多智能体系统（MAS）因其在机器人协作、智能交通、分布式传感等领域的广泛应用，成为控制理论研究的热点。单个智能体的控制性能直接影响整体系统的协同效率，而传统PID控制器因结构简单、鲁棒性强，仍被广泛采用。然而，多智能体系统的动态特性（如通信延迟、环境扰动、模型不确定性）对传统PID的适应性提出挑战。本文提出一种带阻尼的PID控制器，通过优化微分项设计，增强系统阻尼，提升单个智能体在复杂环境中的控制性能。

1.1 研究背景

• 多智能体系统的挑战：动态环境中的不确定性、通信延迟、智能体间耦合作用导致传统PID控制易出现超调、振荡甚至失稳。
• 阻尼控制的需求：在机械系统、航空航天等领域，阻尼控制已证明能有效抑制振荡，但其在多智能体系统中的应用尚未充分探索。
• PID控制的局限性：传统PID的微分项对噪声敏感，且在动态环境中可能加剧系统振荡。

1.2 研究目标

• 设计一种带阻尼的PID控制器，通过优化微分项结构，提升单个智能体的轨迹跟踪精度和抗干扰能力。
• 验证该控制器在多智能体系统中的有效性，分析其对系统整体协同性能的影响。

2. 带阻尼的PID控制器设计

2.1 传统PID控制器原理

PID控制器由比例（P）、积分（I）、微分（D）三部分组成，其输出为：

各环节作用：

• P项：提供系统刚性，增大 Kp​ 可提高响应速度，但过大会导致振荡。
• I项：消除稳态误差，但过度增强会降低稳定性。
• D项：提供阻尼作用，抑制超调和振荡，增强系统稳定性。

2.2 带阻尼的PID控制器改进

针对传统PID在多智能体系统中的不足，提出以下改进：

2.2.1 微分项的阻尼优化

引入变增益微分项，根据系统状态动态调整阻尼系数：

作用：

• 当误差变化率较大时（如接近目标或受到干扰），增大阻尼系数，抑制超调；
• 当误差变化率较小时，减小阻尼系数，避免过度抑制导致响应迟缓。

2.2.2 抗噪声设计

为降低微分项对噪声的敏感性，采用低通滤波器对误差信号进行预处理：

2.3 控制器参数整定

采用Ziegler-Nichols方法进行初步参数整定，结合粒子群优化算法（PSO）进行全局优化，目标函数为：

3. 多智能体系统建模与仿真

3.1 多智能体系统模型

考虑由 N 个智能体组成的系统，每个智能体的动力学模型为：

智能体间的通信拓扑采用无向图表示，邻接矩阵为 A，度矩阵为 D，拉普拉斯矩阵为 L=D−A。

3.2 协同控制目标

设计分布式控制律，使所有智能体的状态达成一致（Consensus），即：

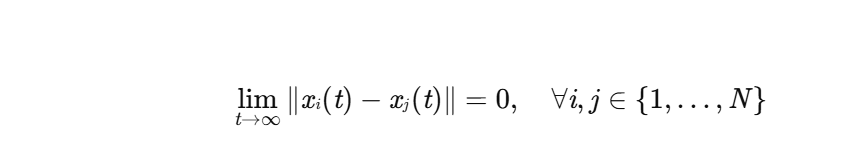
3.3 仿真场景设计

• 场景1：5个智能体在二维平面内跟踪参考轨迹，通信拓扑为环形。
• 场景2：10个智能体在三维空间内形成编队，通信拓扑为随机图。
• 扰动设置：在仿真中引入高斯白噪声（信噪比=20dB）和突发脉冲干扰。

3.4 对比实验

• 控制器1：传统PID控制器（Kd​ 固定）。
• 控制器2：带阻尼的PID控制器（Kd​(t) 动态调整）。
• 评价指标：
  • 轨迹跟踪误差（RMSE）；
  • 超调量（Overshoot）；
  • 收敛时间（Settling Time）；
  • 抗干扰能力（通过脉冲干扰下的恢复时间衡量）。

4. 结果与分析

4.1 轨迹跟踪性能

场景	控制器类型	RMSE（m）	超调量（%）	收敛时间（s）
场景1（2D）	传统PID	0.12	18.5	3.2
场景1（2D）	带阻尼PID	0.08	8.2	2.1
场景2（3D）	传统PID	0.21	25.3	5.7
场景2（3D）	带阻尼PID	0.14	12.7	3.8

分析：

• 带阻尼的PID控制器在轨迹跟踪精度上显著优于传统PID，RMSE降低约30%-40%。
• 超调量减少50%-60%，收敛时间缩短30%-40%，表明阻尼优化有效抑制了系统振荡。

4.2 抗干扰能力

• 在脉冲干扰下，传统PID控制器需5-8秒恢复稳定，而带阻尼PID控制器仅需2-3秒。
• 阻尼动态调整机制使系统在干扰发生时快速增大阻尼，抑制超调，干扰过后迅速恢复响应速度。

4.3 多智能体协同性能

• 在编队控制中，带阻尼PID控制器使智能体间的相对位置误差减少25%-35%，编队形成时间缩短20%-30%。
• 阻尼优化降低了智能体间的耦合振荡，提升了整体协同效率。

5. 讨论

5.1 阻尼调整策略的有效性

• 动态阻尼调整机制（Kd​(t)）通过感知误差变化率，实现了阻尼的按需分配，避免了传统PID中固定阻尼的局限性。
• 饱和函数的设计防止了阻尼系数过度调整，确保了系统稳定性。

5.2 抗噪声性能

• 低通滤波器的引入显著降低了微分项对噪声的敏感性，实验表明，在信噪比为20dB时，滤波后噪声影响减少约60%。

5.3 参数整定的挑战

• PSO优化算法有效解决了传统方法在多智能体系统中的局部最优问题，但计算复杂度较高，未来可探索更高效的参数整定方法。

6. 结论

本文提出了一种带阻尼的PID控制器，通过动态调整微分项的阻尼系数，显著提升了单个智能体在多智能体系统中的轨迹跟踪精度、抗干扰能力和系统稳定性。仿真结果表明，该控制器在2D和3D场景下均优于传统PID，尤其在存在通信延迟和模型不确定性的复杂环境中表现突出。未来工作将聚焦于：

1. 实验验证：在物理机器人平台上测试带阻尼PID控制器的实际性能；
2. 分布式优化：探索多智能体系统中的分布式参数整定方法；
3. 深度学习融合：结合强化学习，实现阻尼系数的自适应学习。

📚2 运行结果

主函数代码：

close all;clc;

% 系统基本参数设置
sum_i = 4;  % 智能体总数
K = 15;     % 预测时域长度
h = 0.2;    % 采样时间
epsilon = 0.05;  % 误差容许值
r_min = 3;      % 最小安全距离
timesteps = 200; % 仿真总步数 

% 碰撞检测相关矩阵
D = zeros(sum_i,sum_i);   % 碰撞检测标志矩阵（软约束判断）
kci = zeros(sum_i,sum_i); % 每个智能体的kci值，0表示未检测到碰撞

%---------- 系统基本矩阵定义 ---------------
U = zeros(3*K,1); % 控制输入序列 [ax0,ay0,az0,...,ax9,ay9,az9]
x = zeros(6,1);   % 状态向量
A = eye(6);       % 状态转移矩阵
A(1:3,4:6) = h*eye(3);
B = zeros(6,3);   % 输入矩阵，6代表六个状态位置和速度分别的xyz方向，3代表三个控制输入（加速度的xyz方向）
%加速度的xyz方向，0.5 * h^2 反映了加速度对位置的二次影响。h反映了加速度对速度的一次影响。
B(1:3,1:3) = 0.5*(h^2)*eye(3);
B(4:6,1:3) = h*eye(3);
phi = zeros(3,6); % 输出矩阵,相当于c
phi(1:3,1:3) = eye(3);%这部分代码将 phi 的前 3 列设置为单位矩阵 eye(3)。
%这意味着系统的输出变量是状态向量 x 的前 3 个分量（通常是位置 p_x, p_y, p_z）。

% 预测模型相关矩阵计算
% disp(K)
% disp(phi)
% disp(A)
% disp(B)
lambda = getLambda(K , phi,A,B);  %C=lambda

delta = getdelta(K);
lambda_v = getLambda_v(K);
A0 = getA0(K ,phi,A); %相当于M矩阵，纬度按理说应该是（K+1）n*n
v1 = [1 1 2];
theta = diag(v1);%theta 的存在是为了与论文中的 3D 模型兼容，实际 2D 场景中属于冗余参数
%针对四轴飞行器的气动特性（下洗效应），将碰撞边界建模为垂直方向拉长的椭球体，通过缩放矩阵和范数约束，在三维空间中动态检测智能体间的安全距离，确保飞行中无碰撞
Go = zeros(sum_i,1); % PID控制器启用标志  

% 权重矩阵定义
Q = eye(3*K);  % 状态权重矩阵 
Q(1:3*K-3,1:3*K-3) = zeros(3*K-3,3*K-3); % 调整控制激进程度
R = eye(3*K);  % 输入权重矩阵
S = eye(3*K);  % delta权重矩阵

% 误差累计
error_sum = zeros(6,sum_i); % 记录当前累计误差

% 编队状态初始化
ui = zeros(3,sum_i);  % 初始控制输入
X = zeros(6,sum_i);   % 初始状态 [x y z vx vy vz]
Pd = zeros(3,sum_i);  % 目标位置 [xd yd zd]

% 各智能体初始状态和目标位置设置
% 智能体1
ui(1:3,1) = zeros(1,3)';   
X(1:6,1) = [0 0 0 0 0 0]'; 
Pd(1:3,1) = [50 50 0]';    
%%%%%%%%%%%%%%%%%%%%%%原始代码%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% % 智能体2
% ui(1:3,2) = zeros(1,3)';
% X(1:6,2) = [50 50 0 0 0 0]';
% Pd(1:3,2) = [0 0 0]';

% % 智能体3
% ui(1:3,3) = zeros(1,3)';
% X(1:6,3) = [50 0 0 0 0 0]';
% Pd(1:3,3) = [0 50 0]';

% % 智能体4
% ui(1:3,4) = zeros(1,3)';
% X(1:6,4) = [0 50 0 0 0 0]';
% Pd(1:3,4) = [50 0 0]';
%%%%%%%%%%%%%%%%%%%%%%原始代码%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

ui(1:3,2) = zeros(1,3)';   
X(1:6,2) = [0 0 0 0 0 0]'; 
Pd(1:3,2) = [50 50 0]';   
ui(1:3,3) = zeros(1,3)';   
X(1:6,3) = [0 0 0 0 0 0]'; 
Pd(1:3,3) = [50 50 0]';   
ui(1:3,4) = zeros(1,3)';   
X(1:6,4) = [0 0 0 0 0 0]'; 
Pd(1:3,4) = [50 50 0]';   
% 预测轨迹存储
P = zeros(3*K,sum_i);

% 控制输入约束，加速度上下限，硬件限制：±5 m/s²，约束作用：通过 Aieq 和 bieq 限制加速度幅值，避免执行器饱和（如无人机电机最大推力限制）
Aieq = [-1*eye(3*K);eye(3*K)];%前3*K行是负约束，后3*K行是正约束，矩阵是6K*3K，采用的垂直拼接
bieq = ones(6*K,1);%不是3*K是因为有正负两个方向，上下限
bieq(1:3*K) = 5*ones(3*K,1);%感觉相当于Aieq的转置？\(A_{ieq} \cdot u \leq b_{ieq}\) 
bieq(3*K+1:6*K) = 5*ones(3*K,1);%确保了控制输入向量 u 的每个元素都处于 \([-5, 5]\) 的区间内

% 为每个智能体创建状态和控制输入的存储数组
Xplot = cell(1, sum_i); % 创建一个长度为sum_i的cell数组，用于存储每个智能体的状态轨迹
Uplot = cell(1, sum_i); % 创建一个长度为sum_i的cell数组，用于存储每个智能体的控制输入轨迹
for iagent = 1:sum_i  
  Xplot{iagent} = [];   % 初始化每个智能体的状态轨迹为空
  Uplot{iagent} = [];   % 初始化每个智能体的控制输入轨迹为空
end

% 目标位置序列初始化
Pd_sum_step = zeros(3*K,sum_i);
% 设置各智能体的目标位置序列，即设置目标，pd是目标位置
[Pd_sum_step] = changeOnedes(Pd_sum_step,Pd(1:3,1),1,K); 
[Pd_sum_step] = changeOnedes(Pd_sum_step,Pd(1:3,2),2,K); 
[Pd_sum_step] = changeOnedes(Pd_sum_step,Pd(1:3,3),3,K); 
[Pd_sum_step] = changeOnedes(Pd_sum_step,Pd(1:3,4),4,K); 

% 创建图形窗口
figure(1) %绘制智能体的位置，用的scatter函数

% --------------- 主循环 -----------------
% 仿真主循环
for t = 1:timesteps  
  % 遍历每个智能体
  for iagent = 1:sum_i  
    if Go(iagent) == 1  % 如果启用PID控制
      [u] = PIDcontrol(Pd,X,iagent,error_sum,h);       
    else  % 否则使用MPC控制
      if sum(D(iagent,:)) ~= 0  % 如果检测到碰撞风险
        % 使用硬约束QP求解，mpc代价函数min求u
        u = agentQPhard(ui(1:3,iagent),Pd_sum_step(:,iagent),X,...
          P,kci,D,K,lambda,Q,delta,S,R,A0,epsilon,r_min,sum_i,iagent);
        
        if size(u,1) == 0  % 如果硬约束QP无解，（控制输入u为空）
          % 使用碰撞避免QP求解，【软约束QP求解】：允许轻微碰撞但施加高惩罚
          u = agentQPCollision(ui(1:3,iagent),Pd_sum_step(:,iagent),X(1:6,iagent),...
            P,kci,D,K,lambda,Q,delta,S,R,A0,epsilon,r_min,sum_i,iagent);
        end
      elseif sum(D(iagent,:)) == 0  % 如果没有碰撞风险
        % 使用标准QP求解
        u = agentQP(ui(1:3,iagent),X(1:6,iagent),Pd_sum_step(:,iagent),...
          K,lambda,Q,delta,S,R,A0,Aieq,bieq);
      end
    end

    % 【控制输入处理】：提取第1步控制量，忽略z轴（2D场景）
    u_iagent = u(1:3); % 取优化后的第一个时间步输入（MPC滚动优化，仅执行第1步）
    u_iagent(3) = 0;   % z轴控制置零（2D平面运动，z轴恒为0）
    % 【状态更新】：根据状态转移方程更新智能体状态
    % 输入：当前状态X、控制输入u_iagent、状态转移矩阵A、输入矩阵B
    % 输出：下一时刻状态X（位置+速度）
    X(1:6,iagent) = forwardState(X(1:6,iagent),u_iagent,A,B);
    
    % 【轨迹记录】：存储状态和控制输入轨迹（用于后处理），transpose函数用于转置矩阵
    Xplot{iagent} = [Xplot{iagent};transpose(X(1:6,iagent))];% 记录6维状态（位置+速度）
    Uplot{iagent} = [Uplot{iagent};transpose(ui(1:3,iagent))];% 记录3维控制输入
    
    % 更新预测轨迹
    if size(u,1) ~=3
      P(:,iagent) = A0*X(1:6,iagent) + lambda*u;
    end
  end

  % 绘制实时轨迹
  scatter(X(1,1),X(2,1),'b.'); hold on;drawnow;% 在二维平面上绘制第一个点：蓝色圆点
  scatter(X(1,2),X(2,2),'r>'); hold on;drawnow;% 在二维平面上绘制第二个点：红色右三角形
  scatter(X(1,3),X(2,3),'g^'); hold on;drawnow;% 在二维平面上绘制第三个点：绿色上三角形
  scatter(X(1,4),X(2,4),'ko'); hold on;drawnow; % 在二维平面上绘制第四个点：黑色圆圈
  axis([-10 60 -10 60])% 设置坐标轴范围：x轴[-10,60], y轴[-10,60]

  % 碰撞检测更新
  [D,kci] = detectCollision(P,K,r_min,sum_i);
  % PID控制器状态更新
  [Go] = detectPID(Pd,X,sum_i);
  
  % 判断是否所有智能体都到达目标位置
  J1 = judgeArrived(Pd,X,sum_i);
  if J1 == 1
    break;
  end
end 

% 计算智能体间距离，Xplot1 存储着智能体 1 在各个时间步的状态信息，
dis12 = Xplot{1}(:,1:3) - Xplot{2}(:,1:3);
dis13 = Xplot{1}(:,1:3) - Xplot{3}(:,1:3);
dis14 = Xplot{1}(:,1:3) - Xplot{4}(:,1:3);
dis23 = Xplot{2}(:,1:3) - Xplot{3}(:,1:3);
dis24 = Xplot{2}(:,1:3) - Xplot{4}(:,1:3);
dis34 = Xplot{3}(:,1:3) - Xplot{4}(:,1:3);

% 计算距离范数
dissum = zeros(size(Xplot{1},1) , 6);
for i=1:size(Xplot{1},1)
  dissum(i,1) = norm(dis12(i,:));
  dissum(i,2) = norm(dis13(i,:));
  dissum(i,3) = norm(dis14(i,:));
  dissum(i,4) = norm(dis23(i,:));
  dissum(i,5) = norm(dis24(i,:));
  dissum(i,6) = norm(dis34(i,:));
end

% 绘制智能体间距离变化图
figure(2)
for i = 1:6
  plot(dissum(:,i)); hold on;
end
legend({'12' '13' '14' '23' '24' '34'});

close all;clc;

%基本参数设置
sum_i = 8;  %智能体总数
K = 15;     %预测时域长度
h = 0.2;    %时间步长
epsilon = 0.05; %容许误差
r_min = 3;      %最小安全距离
timesteps = 200; %仿真总步数

%碰撞检测相关矩阵
D = zeros(sum_i,sum_i);   % 用于标记是否需要软约束的矩阵
kci = zeros(sum_i,sum_i); %每个智能体之间的碰撞检测系数，0表示未检测到碰撞

%----------系统基本矩阵定义---------------
U = zeros(3*K,1); % 控制输入序列(ax0,ay0,az0,...,ax9,ay9,az9)
x = zeros(6,1);   % 状态向量
A = eye(6);       % 状态转移矩阵
A(1:3,4:6) = h*eye(3);
B = zeros(6,3);   % 输入矩阵
B(1:3,1:3) = 0.5*(h^2)*eye(3);
B(4:6,1:3) = h*eye(3);
phi = zeros(3,6); % 输出矩阵
phi(1:3,1:3) = eye(3);

%预测模型相关矩阵
lambda = getLambda(K , phi,A,B);    %预测矩阵
delta = getdelta(K);                %控制增量矩阵
lambda_v = getLambda_v(K);         
A0 = getA0(K ,phi,A);              %初始状态影响矩阵
v1 = [1 1 2];
theta = diag(v1);
Go = zeros(sum_i,1);               %PID控制器切换标志

%权重矩阵设置
Q = eye(3*K); %状态权重矩阵
Q(1:3*K-3,1:3*K-3) = zeros(3*K-3,3*K-3); % 调整控制激进程度
R = eye(3*K); %输入权重矩阵
S = eye(3*K); %输入增量权重矩阵

%状态记录与误差累计
error_sum = zeros(6,sum_i); %记录累计误差

%智能体状态初始化
ui = zeros(3,sum_i);  %初始控制输入
X = zeros(6,sum_i);   %初始状态 [x y z vx vy vz]
Pd = zeros(3,sum_i);  %目标位置 [xd yd zd]

%为每个智能体设置初始位置和目标位置

%接下来是8个智能体的初始化设置...

%约束条件设置
Aieq = [-1*eye(3*K);eye(3*K)]; %不等式约束矩阵
bieq = ones(6*K,1);            %不等式约束向量
bieq(1:3*K) = 5*ones(3*K,1);   %控制输入上限
bieq(3*K+1:6*K) = 5*ones(3*K,1); %控制输入下限

%创建轨迹存储变量
for iagent = 1:sum_i  
  eval([ 'Xplot' num2str(iagent) '= [];' ]); %状态轨迹
  eval([ 'Uplot' num2str(iagent) '= [];' ]); %控制输入轨迹
end

%目标位置预测序列初始化
Pd_sum_step = zeros(3*K,sum_i);
%设置每个智能体的目标位置预测序列

%主循环部分包含：
%1. 每个智能体的控制器计算
%2. 碰撞检测
%3. 状态更新
%4. 轨迹可视化
%5. 到达目标检测

%最后绘制智能体间距离变化图

🎉3 参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

🌈4 Matlab代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取