《Flat-LoRA: Low-Rank Adaptation over a Flat Loss Landscape》略读

引言

我们已经了解到，LoRA（低秩适应）是大模型参数高效微调的经典方案——它无需对模型海量的原始参数逐一更新，只需优化两个维度远低于原权重的低秩矩阵（A与B），即可实现模型的任务适配（具体原理可参考前文解析）。

但这种高效性背后暗藏关键局限：LoRA的优化过程仅聚焦于自身低秩矩阵构成的“局部参数空间”，所找到的“平坦解”也只针对这一局部有效，也就是说，LoRA 的优化空间”就是所有 “秩不超过 $r$” 的 $\Delta W$ 组成的集合，无论如何优化都在都局限在这个 “低复杂度、小尺寸” 的圈子里。完全未考量该解在模型全局参数空间中的损失景观特性。

这一核心症结直接导致隐患：若LoRA找到的局部最优解在全局视角下处于“陡峭区域”，模型的鲁棒性与泛化能力会显著不足——不仅容易被输入数据中的微小噪声干扰，一旦测试数据集与训练集存在分布差异（比如数据场景变化、样本格式调整），性能就可能出现大幅下滑。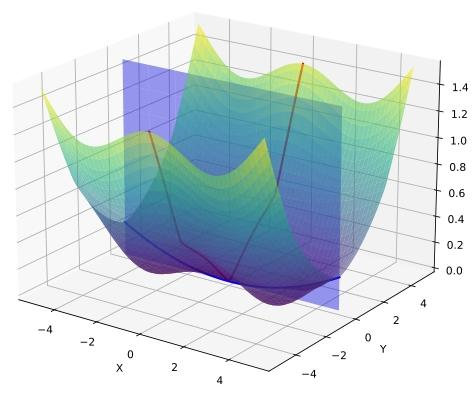

A flat minimum in LoRA space (blue curve) may exhibit
sharp directions in the full parameter space (red curve)

为解决这一问题，上海交通大学黄晓霖团队提出了Flat-LoRA方法，其核心目标是：在保留LoRA参数高效性的基础上，通过针对性优化，让低秩适应的结果在模型全局参数空间中也具备更平滑的损失景观，从而提升模型的抗干扰能力与跨场景适配性。

自然的改进尝试：LoRA-SAM

既然之前有个很成熟的方法叫 SAM（Sharpness-Aware Minimization，“锐度感知最小化”），能让模型找到 “更稳健的解”（在自己的优化空间里 “损失分布更平”），那人们自然会想：把 SAM 的思路用到 LoRA 上，不就能让 LoRA 在自己的 “小圈子” 里更稳健了吗？—— 这就是 “LoRA-SAM” 的由来。

SAM 的核心逻辑很简单：别只找 “损失最低的点”，要找 “损失最低且周围很平的点”—— 具体做法是 “先给参数加个小扰动，找到让损失最大的扰动（模拟‘最坏情况’），再调整参数让这个‘最坏情况的损失’尽可能小”。这样得到的解，稍微动一点参数（遇到新数据、小误差），损失也不会骤升，更稳健。

公式本质是SAM逻辑在LoRA上的“落地”，咱们逐个符号解释：
$$mi{n}_{A,B}ma{x}_{\Vert \left({\epsilon }_A,{\epsilon }_B\right)\Vert \le \rho }L\left(W+\left(B+{\epsilon }_B\right)\left(A+{\epsilon }_A\right)\right)$$

• **$mi{n}_{A,B}$*：“我们最终要优化的是LoRA的两个小矩阵A和B”，目标是让后面的“最大损失”尽可能小（min = 找最小值）。
• $ma{x}_{\Vert \left({\epsilon }_A,{\epsilon }_B\right)\Vert \le \rho }$：“在优化A和B之前，先模拟‘最坏情况’”——给A加个小扰动εₐ（形状和A一样，r×n），给B加个小扰动εᵦ（形状和B一样，m×r），并且这些扰动的“总大小”（用||·||衡量，类似“长度”）不能超过ρ；“max”就是找“能让损失L最大的那组扰动”（模拟“改A/B后效果最差的情况”）。
• $L(\cdot )$：损失函数，就是“衡量模型预测准不准的分数”（比如分类任务的“错误率”，越低越好）。
• $W+\left(B+{\epsilon }_B\right)\left(A+{\epsilon }_A\right)$：“加了扰动后的大模型总参数”——原参数W，加上“被扰动后的LoRA修正矩阵”（代替了原来的$\Delta W=B\times A$）。

看起来很不错对吧，但是咱们接着来看看：

LoRA-SAM 的局限在哪？

LoRA-SAM 的扰动，最终影响了 ( W ) 的哪些部分？

LoRA-SAM 是给 $A,B$加扰动（${\epsilon }_A,{\epsilon }_B$），然后优化 $A,B$。 但$A,B$ 的变化会通过 $\Delta W=BA$影响合并后的 $W$。

这个“等效扰动”为 ${\epsilon }_W$。

LoRA 的修正矩阵是：

$$\Delta W=BA$$

当 $A\to A+{\epsilon }_A$，$B\to B+{\epsilon }_B$ 后，新的 $\Delta W$ 变成：

$$(B+{\epsilon }_B)(A+{\epsilon }_A)=BA+B{\epsilon }_A+{\epsilon }_{B}A+{\epsilon }_B{\epsilon }_A$$

由于 ${\epsilon }_B{\epsilon }_A$是“两个小扰动的乘积”，数值非常小，可以忽略，所以：

$${\epsilon }_W\approx B{\epsilon }_A+{\epsilon }_{B}A$$

接下来用泰勒展开求“最糟的扰动”

SAM 的核心是“先找让损失最大的扰动”（公式里的 $\max$）。
为了计算这个“最糟扰动”，论文用了“一阶泰勒展开”，最终推导出 ${\epsilon }_W$ 的具体表达式：

$${\epsilon }_W=c\left[B{B}^{\top }{\nabla }_{W}L+{\nabla }_{W}L{A}^{\top }A\right]+c^2{\nabla }_{W}L{A}^{\top }{B}^{\top }{\nabla }_{W}L$$

$c$：缩放因子，控制扰动大小不超过 $\rho$（扰动幅度上限）。

从 ${\epsilon }_W$ 的表达式能看出来：它所有的项，都是 “$B$ 和 $A$ 的组合” 与 “梯度${\nabla }_{W}L$” 的乘积。换句话说，${\epsilon }_W$ 的方向，只局限在 “$A$ 的列空间” 和 “$B$ 的行空间” 组成的小 subspace 里

这就证明了：LoRA-SAM 的 “抗扰动训练”，只覆盖了全参数空间里 “和 A、B 相关的一小部分方向”，没覆盖其他方向。所以，即使在这一小部分方向上是 “平的”，全参数空间里的其他方向可能还是陡峭的

Flat-LoRA

为了解决上述问题，在完整的参数空间中考虑损失景观并确定将合并权重置于平坦区域的低秩适应至关重要。为实现这一目标，我们提出以下平坦损失目标：

$$mi{n}_{A,B}ma{x}_{{\Vert {\epsilon }_W\Vert }_F\le \rho }L\left(W+BA+{\epsilon }_W\right)$$

其中，${\epsilon }_W\in {\mathbb{R}}^{m\times n}$ 是对噪声的对抗性扰动。

其中F范数定义为：$$\Vert X{\Vert }_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^n{X}_{ij}^2}$$

这个公式的逻辑是“先找让损失最大的扰动${\epsilon }_W$（最坏情况），再优化$A、B$让这个最坏损失最小”——这正是SAM的思路，但它有两个致命问题：

1. 费时间：找“最坏扰动”需要多算一轮梯度（相当于训练时间翻倍）；
2. 费内存：要存下给全参数$W$加的扰动${\epsilon }_W$（W是m×n的大矩阵，存起来占巨多空间）。

这完全违背了LoRA“参数高效”的初衷。所以Flat-LoRA要做的是：找个替代方案，既能达到“让全空间平坦”的目的，又不用算“最坏情况”

换个更简单的方式实现同样目标——把“找最坏情况的max”换成“算很多随机情况的平均（期望）”。

$$mi{n}_{A,B}{\mathbb{E}}_{{\left({\epsilon }_W\right)}_{i,j}\sim \mathcal{N}\left(0,{\sigma }^2\right)}L\left(W+BA+{\epsilon }_W\right)$$

整体逻辑：
“优化LoRA的A和B，让‘给全参数加很多次随机小扰动后，模型的平均损失’尽可能小。”

之前用SAM的“找最坏扰动”太费资源，所以Flat-LoRA换了个思路：让模型在训练时反复适应“全参数的随机小波动”，通过优化“平均损失”，既磨平了全参数空间的损失尖峰（得到平坦景观），又没多花时间、多占内存，完美契合LoRA“高效”的核心需求。

后文将介绍如何在参数上加这个随机扰动

如何添加随机扰动

先介绍一个引理：

若损失函数L(W)关于W是α-Lipschitz连续且β-smooth的，则“加高斯扰动后的期望损失函数”（即${\mathbb{E}}_{{\epsilon }_W\sim \mathcal{N}(0,{\sigma }^2)}L(W+{\epsilon }_W)$）是$min(\frac{\alpha }{\sigma },\beta )$-smooth的。

$\alpha -Lipschitz$连续（函数“不会突变”）
“Lipschitz连续”的核心是：函数的变化速度有“上限”，不会出现“垂直悬崖”式的突变。

$\beta -smooth$（函数的“坡度不会突变”）
“β-smooth”比Lipschitz连续更严格，它约束的是函数“坡度”（梯度）的变化速度——梯度本身也不会突变，函数曲线是“平滑的曲面”而非“有棱角的多面体”。

“如果原损失函数本身变化不算太剧烈（满足α-Lipschitz和β-smooth），那么Flat-LoRA用‘加随机扰动算平均损失’的方法，能让损失函数变得更平滑（平滑常数变小），从而从理论上保证能找到更平坦的最优解——这正是Flat-LoRA想要的效果。”

Flat-LoRA的随机权重扰动有两个核心设计：

一是按“滤波器”（实际上是权重$W$（$m\ast n,m=输出维度，n=输入维度$)矩阵的行向量，即特征提取单元）生成扰动，范数越大的核心滤波器，扰动强度越强，精准考验关键部件稳健性；

二是将扰动方差缩放1/n（n为输入维度），抵消输入规模对扰动效果的影响，保证不同场景下扰动强度稳定。两者结合让扰动高效且精准，助力平滑全局损失景观。

那么我们就可以得到公式:

• 未加扰动时，激活值方差：
  $var[W_{j,:}^{\prime }x]=\Vert W_{j,:}^{\prime }{\Vert }_2^2\cdot var[x_i]$（由滤波器强度与输入波动决定）

• 加扰动后，激活值方差：
  $var[(W^{\prime }+{\epsilon }_W{)}_{j,:}x]=(1+{\sigma }^2)\Vert W_{j,:}^{\prime }{\Vert }_2^2\cdot var[x_i]+{\sigma }^2\Vert W_{j,:}^{\prime }{\Vert }_2^2\cdot E^2[x_i]$

• 核心：扰动放大激活值方差（因子$1+{\sigma }^2$），助力跳出尖锐局部最优；1/n缩放使增幅与输入维度n无关，保证稳定性。

此外，我们注意到，由于层归一化的存在，这种方差在网络的前向传播过程中不会呈指数增长。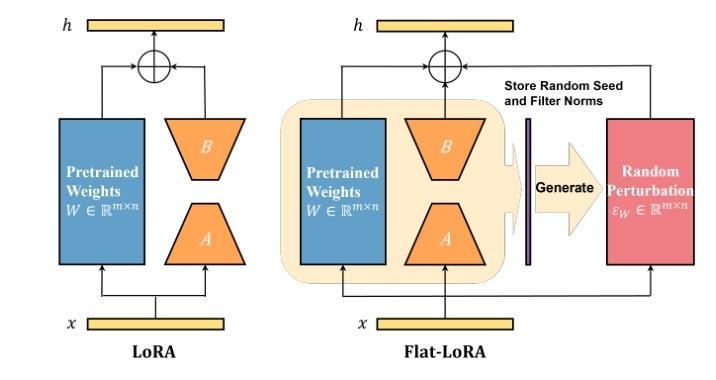

至此，Flat-LoRA的理论部分就介绍完了，后续的内容是实验，后面再研究研究