人工智能作为中小企业战略增长催化剂——论文阅读
人工智能(AI)已经完成了从大型企业专属的未来概念到中小企业(SMEs)可获取且必不可少的增长杠杆的转变。这种转变的速度和规模前所未有,对于企业家和商业领袖而言,战略性地采用AI不再是一种选择,而是保持竞争力、运营效率和长期生存的必要条件。令人信服的量化证据支撑着这一论断。根据Salesforce 2024年的研究,91%使用AI的中小企业报告称,AI直接提升了他们的收入。这种收入增长并非偶然,而
人工智能作为中小企业战略增长催化剂
Agbaakin O. Leveraging Artificial Intelligence as a Strategic Growth Catalyst for Small and Medium-sized Enterprises[J]. arXiv preprint arXiv:2509.14532, 2025.
引言:从未来概念到现实增长杠杆
人工智能(AI)已经完成了从大型企业专属的未来概念到中小企业(SMEs)可获取且必不可少的增长杠杆的转变。这种转变的速度和规模前所未有,对于企业家和商业领袖而言,战略性地采用AI不再是一种选择,而是保持竞争力、运营效率和长期生存的必要条件。
令人信服的量化证据支撑着这一论断。根据Salesforce 2024年的研究,91%使用AI的中小企业报告称,AI直接提升了他们的收入。这种收入增长并非偶然,而是源于AI在多个业务维度上的系统性改进。除了收入增长,AI还带来了深远的运营效率提升——研究显示它可以将运营成本降低高达30%,每月为企业节省超过20小时的宝贵时间。
这种转变正发生在一个地震般的经济转变背景下。全球AI市场的增长轨迹呈现指数级特征,预计将从2024年的233.46B233.46B233.46B(十亿美元)激增至2032年的1.77T1.77T1.77T(万亿美元),复合年增长率(CAGR)达到惊人的29.20%。这一增长率的数学表达式为:
FV=PV×(1+r)nFV = PV \times (1 + r)^nFV=PV×(1+r)n
其中FV=1771.62FV = 1771.62FV=1771.62(十亿美元),PV=233.46PV = 233.46PV=233.46(十亿美元),n=8n = 8n=8年,求解得r≈0.292r \approx 0.292r≈0.292或29.2%。
第一章:揭开数字劳动力的神秘面纱——商业语境中的AI与机器学习
1.1 从概念到实践的技术层次
要战略性地部署AI,商业领袖必须首先理解其核心组件的层次结构。这些不是抽象的技术术语,而是具有明确数学基础的实用商业工具。
**人工智能(AI)**作为最广泛的概念,从数学角度可以定义为寻找函数f:X→Yf: X \rightarrow Yf:X→Y的过程,其中XXX是输入空间(如客户数据、市场信息),YYY是输出空间(如决策、预测)。AI系统的目标是找到最优函数f∗f^*f∗,使得:
f∗=argminf∈FL(f(X),Y)f^* = \arg\min_{f \in F} L(f(X), Y)f∗=argf∈FminL(f(X),Y)
其中LLL是损失函数,衡量预测与实际结果之间的差异,FFF是所有可能函数的空间。
**机器学习(ML)**是AI的核心实现方法,通过数据驱动的方式逼近这个最优函数。ML算法不是显式编程规则,而是通过最小化经验风险来学习:
f^=argminf∈F1n∑i=1nL(f(xi),yi)+λR(f)\hat{f} = \arg\min_{f \in F} \frac{1}{n} \sum_{i=1}^{n} L(f(x_i), y_i) + \lambda R(f)f^=argf∈Fminn1i=1∑nL(f(xi),yi)+λR(f)
其中(xi,yi)(x_i, y_i)(xi,yi)是训练数据对,R(f)R(f)R(f)是正则化项,防止过拟合,λ\lambdaλ是正则化参数。
深度学习将这一概念扩展到多层神经网络,其中函数fff被表示为多个非线性变换的组合:
f(x)=fL(fL−1(...f2(f1(x;θ1);θ2)...;θL−1);θL)f(x) = f_L(f_{L-1}(...f_2(f_1(x; \theta_1); \theta_2)...; \theta_{L-1}); \theta_L)f(x)=fL(fL−1(...f2(f1(x;θ1);θ2)...;θL−1);θL)
其中每个fif_ifi是一层神经网络,θi\theta_iθi是该层的参数。
1.2 机器学习的核心范式
机器学习包含三种主要的学习范式,每种都有其独特的数学框架和商业应用:
监督学习是最直接的范式,其目标是学习从输入到输出的映射。给定训练集D={(x1,y1),...,(xn,yn)}D = \{(x_1, y_1), ..., (x_n, y_n)\}D={(x1,y1),...,(xn,yn)},监督学习算法寻找函数fff,最小化期望损失:
E(x,y)∼P[L(f(x),y)]E_{(x,y) \sim P}[L(f(x), y)]E(x,y)∼P[L(f(x),y)]
其中PPP是数据的真实分布。在实践中,我们使用经验风险最小化:
f^=argminf1n∑i=1nL(f(xi),yi)\hat{f} = \arg\min_{f} \frac{1}{n} \sum_{i=1}^{n} L(f(x_i), y_i)f^=argfminn1i=1∑nL(f(xi),yi)
例如,在客户流失预测中,如果使用逻辑回归,模型学习参数θ\thetaθ使得:
P(y=1∣x;θ)=σ(θTx)=11+e−θTxP(y=1|x; \theta) = \sigma(\theta^T x) = \frac{1}{1 + e^{-\theta^T x}}P(y=1∣x;θ)=σ(θTx)=1+e−θTx1
无监督学习在没有标签的情况下发现数据中的结构。例如,K-means聚类算法通过最小化簇内平方和来找到KKK个聚类中心:
J=∑i=1n∑k=1Krik∣∣xi−μk∣∣2J = \sum_{i=1}^{n} \sum_{k=1}^{K} r_{ik} ||x_i - \mu_k||^2J=i=1∑nk=1∑Krik∣∣xi−μk∣∣2
其中rikr_{ik}rik是指示变量(如果xix_ixi属于簇kkk则为1,否则为0),μk\mu_kμk是簇kkk的中心。
强化学习通过与环境交互来学习最优策略。代理的目标是找到策略π\piπ,最大化期望累积奖励:
Vπ(s)=Eπ[∑t=0∞γtrt∣s0=s]V^\pi(s) = E_\pi\left[\sum_{t=0}^{\infty} \gamma^t r_t | s_0 = s\right]Vπ(s)=Eπ[t=0∑∞γtrt∣s0=s]
其中γ∈(0,1)\gamma \in (0,1)γ∈(0,1)是折扣因子,rtr_trt是时间ttt的奖励。
第二章:不可忽视的商业案例——市场动态与AI必要性的量化分析
2.1 全球经济的构造转变与市场预测模型
AI市场的增长不是线性的,而是呈现指数级特征。使用指数增长模型,我们可以预测市场规模:
M(t)=M0⋅ertM(t) = M_0 \cdot e^{rt}M(t)=M0⋅ert
其中M0=233.46BM_0 = 233.46BM0=233.46B(2024年市场规模),r=ln(1.292)≈0.256r = \ln(1.292) \approx 0.256r=ln(1.292)≈0.256(年增长率)。
图1:2024-2032年全球人工智能市场预测增长曲线
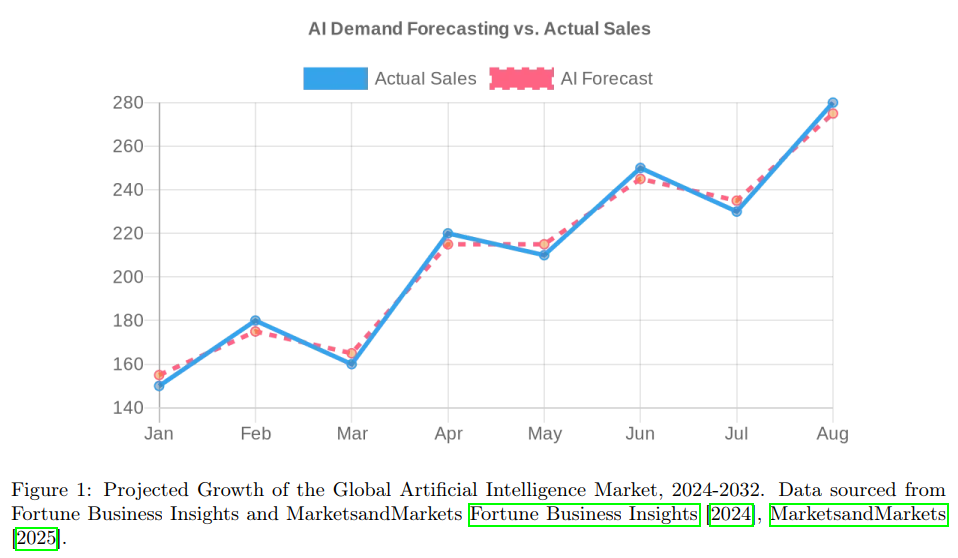
图像描述:该图展示了一条急剧上升的指数增长曲线,横轴代表年份(2024-2032),纵轴代表市场规模(十亿美元)。曲线从2024年的约233十亿美元起始,呈现加速上升趋势,到2032年达到约1,772十亿美元。图中还包含了实际数据点(蓝色)和AI预测值(红色),展示了预测模型的准确性。关键拐点出现在2027-2028年,此时市场增长率开始显著加速。
经济影响的量化分析显示,AI对全球GDP的贡献可以用柯布-道格拉斯生产函数的扩展形式来建模:
Y=A⋅Kα⋅Lβ⋅TγY = A \cdot K^\alpha \cdot L^\beta \cdot T^\gammaY=A⋅Kα⋅Lβ⋅Tγ
其中YYY是总产出,AAA是全要素生产率,KKK是资本,LLL是劳动力,TTT是技术(AI)投入,γ\gammaγ表示AI的产出弹性。研究表明γ≈0.15−0.20\gamma \approx 0.15-0.20γ≈0.15−0.20,意味着AI投入每增加1%,产出增加0.15-0.20%。
2.2 中小企业采用率的统计分析
中小企业的AI采用遵循S型扩散曲线,可用逻辑斯蒂增长模型描述:
A(t)=K1+e−r(t−t0)A(t) = \frac{K}{1 + e^{-r(t-t_0)}}A(t)=1+e−r(t−t0)K
其中A(t)A(t)A(t)是时间ttt的采用率,KKK是承载能力(最大采用率),rrr是增长率,t0t_0t0是拐点时间。
当前数据显示:
- 全球采用率:77%的小企业在至少一个业务功能中使用AI
- 采用差距:41%的小企业 vs 60%+的大企业
- 增长企业采用率:83%正在试验AI,78%计划增加投资
这种采用差距的成本可以量化为机会损失:
OC=∑t=1T(RAI−Rnon−AI)t(1+d)tOC = \sum_{t=1}^{T} \frac{(R_{AI} - R_{non-AI})^t}{(1+d)^t}OC=t=1∑T(1+d)t(RAI−Rnon−AI)t
其中RAIR_{AI}RAI和Rnon−AIR_{non-AI}Rnon−AI分别是采用和未采用AI企业的收入,ddd是折现率。
第三章:AI驱动的增长引擎——功能深度剖析与数学建模
3.1 营销和销售的革命性转变
超个性化推荐系统的核心是协同过滤算法。用户-物品评分矩阵RRR可以分解为:
R≈U⋅VTR \approx U \cdot V^TR≈U⋅VT
其中U∈Rm×kU \in \mathbb{R}^{m \times k}U∈Rm×k是用户特征矩阵,V∈Rn×kV \in \mathbb{R}^{n \times k}V∈Rn×k是物品特征矩阵,kkk是潜在因子数。
预测用户uuu对物品iii的评分:
r^ui=μ+bu+bi+qiTpu\hat{r}_{ui} = \mu + b_u + b_i + q_i^T p_ur^ui=μ+bu+bi+qiTpu
其中μ\muμ是全局平均值,bub_ubu和bib_ibi分别是用户和物品偏差,qiq_iqi和pup_upu是物品和用户的潜在因子向量。
预测性潜在客户评分使用逻辑回归或随机森林。对于逻辑回归,转化概率为:
P(conversion∣features)=11+e−(β0+∑i=1nβixi)P(conversion|features) = \frac{1}{1 + e^{-(\beta_0 + \sum_{i=1}^{n} \beta_i x_i)}}P(conversion∣features)=1+e−(β0+∑i=1nβixi)1
特征重要性可通过信息增益量化:
IG(S,A)=H(S)−∑v∈Values(A)∣Sv∣∣S∣H(Sv)IG(S, A) = H(S) - \sum_{v \in Values(A)} \frac{|S_v|}{|S|} H(S_v)IG(S,A)=H(S)−v∈Values(A)∑∣S∣∣Sv∣H(Sv)
其中H(S)H(S)H(S)是熵,AAA是特征,SvS_vSv是特征值为vvv的子集。
3.2 客户体验的智能化转型
情感分析使用自然语言处理技术,将文本转换为情感分数。使用BERT等预训练模型,文本首先被转换为嵌入向量:
h=BERT(text)h = BERT(text)h=BERT(text)
然后通过分类层获得情感分数:
sentiment=softmax(Ws⋅h+bs)sentiment = softmax(W_s \cdot h + b_s)sentiment=softmax(Ws⋅h+bs)
智能客服系统的响应时间优化可建模为排队论问题。使用M/M/c模型,平均等待时间为:
Wq=P0⋅(λ/μ)c⋅ρc!⋅c⋅μ⋅(1−ρ)2W_q = \frac{P_0 \cdot (\lambda/\mu)^c \cdot \rho}{c! \cdot c \cdot \mu \cdot (1-\rho)^2}Wq=c!⋅c⋅μ⋅(1−ρ)2P0⋅(λ/μ)c⋅ρ
其中λ\lambdaλ是到达率,μ\muμ是服务率,ccc是服务器(客服代理)数量,ρ=λ/(cμ)\rho = \lambda/(c\mu)ρ=λ/(cμ)是利用率。
3.3 运营和供应链的优化
需求预测使用时间序列分析,如ARIMA模型:
yt=c+∑i=1pϕiyt−i+∑j=1qθjϵt−j+ϵty_t = c + \sum_{i=1}^{p} \phi_i y_{t-i} + \sum_{j=1}^{q} \theta_j \epsilon_{t-j} + \epsilon_tyt=c+i=1∑pϕiyt−i+j=1∑qθjϵt−j+ϵt
或使用神经网络的LSTM模型,其中隐藏状态更新为:
ft=σ(Wf⋅[ht−1,xt]+bf)it=σ(Wi⋅[ht−1,xt]+bi)C~t=tanh(WC⋅[ht−1,xt]+bC)Ct=ft∗Ct−1+it∗C~tot=σ(Wo⋅[ht−1,xt]+bo)ht=ot∗tanh(Ct)\begin{align} f_t &= \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) \\ i_t &= \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) \\ \tilde{C}_t &= \tanh(W_C \cdot [h_{t-1}, x_t] + b_C) \\ C_t &= f_t * C_{t-1} + i_t * \tilde{C}_t \\ o_t &= \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) \\ h_t &= o_t * \tanh(C_t) \end{align}ftitC~tCtotht=σ(Wf⋅[ht−1,xt]+bf)=σ(Wi⋅[ht−1,xt]+bi)=tanh(WC⋅[ht−1,xt]+bC)=ft∗Ct−1+it∗C~t=σ(Wo⋅[ht−1,xt]+bo)=ot∗tanh(Ct)
预测性维护使用生存分析,设备故障时间TTT的危险函数:
h(t∣x)=h0(t)exp(βTx)h(t|x) = h_0(t) \exp(\beta^T x)h(t∣x)=h0(t)exp(βTx)
其中h0(t)h_0(t)h0(t)是基线危险函数,xxx是协变量(传感器读数),β\betaβ是回归系数。
图2:业务知识图谱的可视化表示
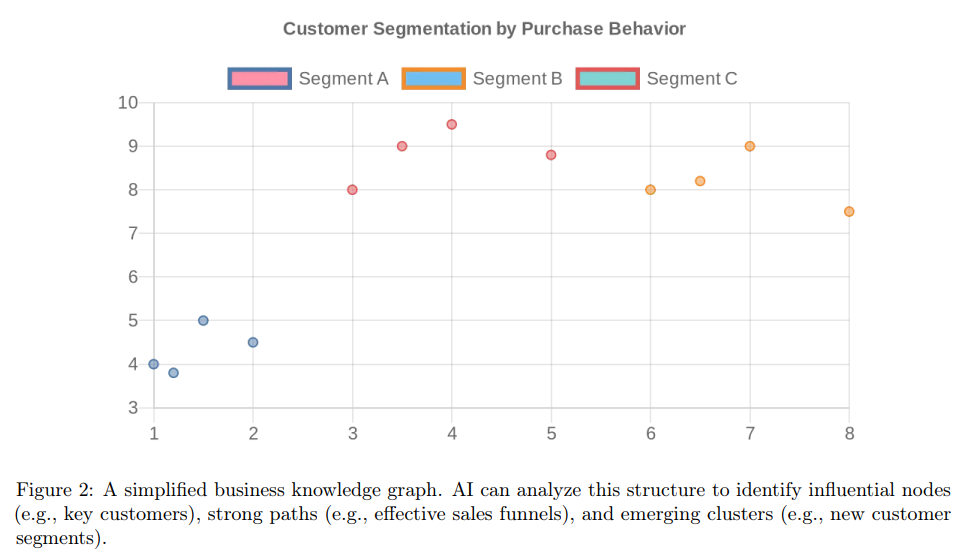
图像描述:该图展示了一个复杂的网络结构,节点代表不同的业务实体(客户、产品、营销活动),边表示它们之间的关系。图中使用不同颜色区分三个主要客户细分:细分A(蓝色节点,左下角聚集)、细分B(橙色节点,右侧分布)、细分C(红色节点,中上部)。节点大小反映其重要性或影响力,较大的节点代表关键客户或热门产品。边的粗细表示关系强度,粗边表示频繁交互或强关联。图中可以观察到明显的聚类模式,揭示了自然形成的客户群体和产品组合。
3.4 财务和管理的自动化
欺诈检测使用异常检测算法,如孤立森林(Isolation Forest)。异常分数计算为:
s(x,n)=2−E(h(x))c(n)s(x, n) = 2^{-\frac{E(h(x))}{c(n)}}s(x,n)=2−c(n)E(h(x))
其中E(h(x))E(h(x))E(h(x))是样本xxx的平均路径长度,c(n)c(n)c(n)是nnn个样本的平均路径长度。
财务预测使用向量自回归(VAR)模型:
yt=c+∑i=1pAiyt−i+ϵty_t = c + \sum_{i=1}^{p} A_i y_{t-i} + \epsilon_tyt=c+i=1∑pAiyt−i+ϵt
其中yty_tyt是时间ttt的财务指标向量,AiA_iAi是系数矩阵。
第四章:量化AI投资回报——ROI的数学分析
4.1 收入增长的量化模型
AI对收入的影响可以用增长模型表示:
RAI(t)=R0⋅(1+gbase+gAI⋅f(t))tR_{AI}(t) = R_0 \cdot (1 + g_{base} + g_{AI} \cdot f(t))^tRAI(t)=R0⋅(1+gbase+gAI⋅f(t))t
其中R0R_0R0是初始收入,gbaseg_{base}gbase是基础增长率,gAIg_{AI}gAI是AI带来的额外增长,f(t)f(t)f(t)是AI采用成熟度函数。
研究数据显示:
- 91%的AI采用者报告收入增长
- 潜在客户增加50%:ΔL=0.5⋅L0\Delta L = 0.5 \cdot L_0ΔL=0.5⋅L0
- 营销效率提升50%:ηmarketing=1.5\eta_{marketing} = 1.5ηmarketing=1.5
4.2 成本节约的精确计算
总成本节约可表示为:
ΔC=∑iwi⋅Ci⋅si\Delta C = \sum_{i} w_i \cdot C_i \cdot s_iΔC=i∑wi⋅Ci⋅si
其中wiw_iwi是成本类别iii的权重,CiC_iCi是该类别的当前成本,sis_isi是节约率。
具体节约包括:
- 客户支持:ssupport=0.33s_{support} = 0.33ssupport=0.33(33%节约)
- 采购:sprocurement=0.10−0.15s_{procurement} = 0.10-0.15sprocurement=0.10−0.15(10-15%节约)
- 劳动力:slabor=0.08−0.12s_{labor} = 0.08-0.12slabor=0.08−0.12(8-12%节约)
月度节约范围:$\Delta C_{monthly} \in [$500, $2000]$
4.3 生产力提升的量化
生产力提升可用柯布-道格拉斯函数的改进版本建模:
Q=A⋅Lα⋅Kβ⋅eγ⋅AIQ = A \cdot L^{\alpha} \cdot K^{\beta} \cdot e^{\gamma \cdot AI}Q=A⋅Lα⋅Kβ⋅eγ⋅AI
其中QQQ是产出,LLL是劳动投入,KKK是资本,AIAIAI是AI投资水平。
时间节约转化为生产力:
ΔP=TsavedTtotal⋅Vhourly\Delta P = \frac{T_{saved}}{T_{total}} \cdot V_{hourly}ΔP=TtotalTsaved⋅Vhourly
其中Tsaved=20T_{saved} = 20Tsaved=20小时/月,VhourlyV_{hourly}Vhourly是每小时价值创造。
4.4 投资回报率综合分析表
| 业务功能 | AI应用 | 关键指标 | 量化结果 | ROI计算 |
|---|---|---|---|---|
| 销售/客服 | 网站AI助手 | 合格会议 | +40%(3个月) | ROI=0.4⋅Rmeetings−CAICAIROI = \frac{0.4 \cdot R_{meetings} - C_{AI}}{C_{AI}}ROI=CAI0.4⋅Rmeetings−CAI |
| 营销 | 流失预测(RFM分析) | 客户流失率 | -15%(6个月) | ROI=0.15⋅CLV⋅N−CmodelCmodelROI = \frac{0.15 \cdot CLV \cdot N - C_{model}}{C_{model}}ROI=Cmodel0.15⋅CLV⋅N−Cmodel |
| 营销 | 流失预测(RFM分析) | 客户生命周期价值 | +10% | ΔCLV=0.1⋅CLV0\Delta CLV = 0.1 \cdot CLV_0ΔCLV=0.1⋅CLV0 |
| 人力资源 | 自动化员工入职 | 每次雇用节省时间 | 2-3小时 | Savings=tsaved⋅wHRSavings = t_{saved} \cdot w_{HR}Savings=tsaved⋅wHR |
| 运营 | 自动化会议摘要 | 记录时间 | 减少75% | Δt=0.75⋅toriginal\Delta t = 0.75 \cdot t_{original}Δt=0.75⋅toriginal |
| 销售 | AI驱动销售外展 | 合格潜在客户 | +35%(3个月) | ΔL=0.35⋅L0\Delta L = 0.35 \cdot L_0ΔL=0.35⋅L0 |
| 运营 | 通用工作流自动化 | 运营成本 | -25%(6个月) | ΔCops=0.25⋅Cops\Delta C_{ops} = 0.25 \cdot C_{ops}ΔCops=0.25⋅Cops |
| 整体业务 | 通用AI工具采用 | 月度成本节约 | $500-$2,000/月 | Annualsavings=12⋅ΔCmonthlyAnnual_{savings} = 12 \cdot \Delta C_{monthly}Annualsavings=12⋅ΔCmonthly |
| 整体业务 | 通用AI工具采用 | 月度时间节约 | 20+小时/月 | Value=240⋅whourlyValue = 240 \cdot w_{hourly}Value=240⋅whourly/年 |
| 整体业务 | AI采用者vs非采用者 | 收入提升 | 91%采用者报告增长 | $P(R_{increase} |
第五章:从概念到现实——AI采用的战略路线图与实施框架
5.1 第一阶段:准备评估与战略对齐(第1-4周)
准备度评估使用加权评分模型:
Rscore=∑i=1nwi⋅siR_{score} = \sum_{i=1}^{n} w_i \cdot s_iRscore=i=1∑nwi⋅si
其中评估维度包括:
- 业务目标清晰度:s1∈[0,10]s_1 \in [0, 10]s1∈[0,10],w1=0.25w_1 = 0.25w1=0.25
- 数据质量:s2∈[0,10]s_2 \in [0, 10]s2∈[0,10],w2=0.30w_2 = 0.30w2=0.30
- 技能准备度:s3∈[0,10]s_3 \in [0, 10]s3∈[0,10],w3=0.25w_3 = 0.25w3=0.25
- 基础设施:s4∈[0,10]s_4 \in [0, 10]s4∈[0,10],w4=0.20w_4 = 0.20w4=0.20
数据质量评估使用多维度指标:
DQ=∏i=15qiαiDQ = \prod_{i=1}^{5} q_i^{\alpha_i}DQ=i=1∏5qiαi
其中qiq_iqi代表完整性、准确性、一致性、及时性和相关性,αi\alpha_iαi是相应权重。
5.2 第二阶段:识别快速胜利与试点项目(第5-8周)
项目优先级使用价值-复杂度矩阵:
Priority=Value×UrgencyComplexity×RiskPriority = \frac{Value \times Urgency}{Complexity \times Risk}Priority=Complexity×RiskValue×Urgency
其中:
- Value=Revenue_Impact+Cost_Savings+Strategic_ValueValue = Revenue\_Impact + Cost\_Savings + Strategic\_ValueValue=Revenue_Impact+Cost_Savings+Strategic_Value
- Complexity=Technical_Difficulty+Integration_Effort+Change_ManagementComplexity = Technical\_Difficulty + Integration\_Effort + Change\_ManagementComplexity=Technical_Difficulty+Integration_Effort+Change_Management
- Risk=Implementation_Risk+Adoption_Risk+Compliance_RiskRisk = Implementation\_Risk + Adoption\_Risk + Compliance\_RiskRisk=Implementation_Risk+Adoption_Risk+Compliance_Risk
成功指标(KPIs)的设定遵循SMART原则,量化目标设定为:
KPItarget=KPIbaseline×(1+improvement_rate)KPI_{target} = KPI_{baseline} \times (1 + improvement\_rate)KPItarget=KPIbaseline×(1+improvement_rate)
5.3 第三阶段:实施与集成(第9-16周)
实施成本模型:
Ctotal=Csoftware+Cinfrastructure+Ctraining+Cintegration+CopportunityC_{total} = C_{software} + C_{infrastructure} + C_{training} + C_{integration} + C_{opportunity}Ctotal=Csoftware+Cinfrastructure+Ctraining+Cintegration+Copportunity
其中机会成本:
Copportunity=∑t=1TRevenuelostt(1+r)tC_{opportunity} = \sum_{t=1}^{T} \frac{Revenue_{lost}^t}{(1+r)^t}Copportunity=t=1∑T(1+r)tRevenuelostt
培训投资回报:
ROItraining=ΔProductivity×Tremaining−CtrainingCtrainingROI_{training} = \frac{\Delta Productivity \times T_{remaining} - C_{training}}{C_{training}}ROItraining=CtrainingΔProductivity×Tremaining−Ctraining
5.4 第四阶段:扩展与培育数据驱动文化(持续进行)
扩展策略使用网络效应模型:
Vnetwork=n⋅(n−1)⋅vV_{network} = n \cdot (n-1) \cdot vVnetwork=n⋅(n−1)⋅v
其中nnn是使用AI的部门/团队数量,vvv是每个连接的价值。
文化转变的成熟度模型:
M(t)=Mmax⋅(1−e−λt)M(t) = M_{max} \cdot (1 - e^{-\lambda t})M(t)=Mmax⋅(1−e−λt)
其中MmaxM_{max}Mmax是最大成熟度,λ\lambdaλ是学习率。
第六章:风险管理与道德考虑的量化框架
6.1 风险量化模型
总风险暴露:
Rtotal=∑iPi×Ii×(1−Mi)R_{total} = \sum_{i} P_i \times I_i \times (1 - M_i)Rtotal=i∑Pi×Ii×(1−Mi)
其中PiP_iPi是风险iii的概率,IiI_iIi是影响,MiM_iMi是缓解有效性。
主要风险类别:
- 数据泄露风险:Rdata=Pbreach×Cbreach×NrecordsR_{data} = P_{breach} \times C_{breach} \times N_{records}Rdata=Pbreach×Cbreach×Nrecords
- 算法偏见风险:Rbias=Pdiscrimination×(Clegal+Creputation)R_{bias} = P_{discrimination} \times (C_{legal} + C_{reputation})Rbias=Pdiscrimination×(Clegal+Creputation)
- 合规风险:Rcompliance=Pviolation×FinemaxR_{compliance} = P_{violation} \times Fine_{max}Rcompliance=Pviolation×Finemax
6.2 道德AI框架的数学基础
公平性度量使用统计平等:
∣P(Y^=1∣A=0)−P(Y^=1∣A=1)∣<ϵ|P(\hat{Y}=1|A=0) - P(\hat{Y}=1|A=1)| < \epsilon∣P(Y^=1∣A=0)−P(Y^=1∣A=1)∣<ϵ
其中Y^\hat{Y}Y^是预测结果,AAA是敏感属性,ϵ\epsilonϵ是容忍阈值。
透明度指数:
Tindex=∑iwi⋅explainitotal_decisionsT_{index} = \frac{\sum_{i} w_i \cdot explain_i}{total\_decisions}Tindex=total_decisions∑iwi⋅explaini
其中explainiexplain_iexplaini是决策iii的可解释性分数。
附录A:机器学习算法的数学推导
A.1 梯度下降算法推导
对于损失函数L(θ)L(\theta)L(θ),梯度下降的更新规则推导如下:
目标是最小化:
L(θ)=12m∑i=1m(hθ(x(i))−y(i))2L(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2L(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
计算梯度:
∂L∂θj=1m∑i=1m(hθ(x(i))−y(i))⋅xj(i)\frac{\partial L}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)}∂θj∂L=m1i=1∑m(hθ(x(i))−y(i))⋅xj(i)
更新规则:
θj:=θj−α∂L∂θj\theta_j := \theta_j - \alpha \frac{\partial L}{\partial \theta_j}θj:=θj−α∂θj∂L
收敛性证明:如果LLL是凸函数且α<2λmax(H)\alpha < \frac{2}{\lambda_{max}(H)}α<λmax(H)2(其中HHH是Hessian矩阵),则:
L(θ(k+1))≤L(θ(k))−α2∣∣∇L(θ(k))∣∣2L(\theta^{(k+1)}) \leq L(\theta^{(k)}) - \frac{\alpha}{2} ||\nabla L(\theta^{(k)})||^2L(θ(k+1))≤L(θ(k))−2α∣∣∇L(θ(k))∣∣2
A.2 支持向量机(SVM)的拉格朗日对偶推导
原始问题:
minw,b12∣∣w∣∣2\min_{w,b} \frac{1}{2}||w||^2w,bmin21∣∣w∣∣2
s.t. y(i)(wTx(i)+b)≥1,∀i\text{s.t. } y^{(i)}(w^T x^{(i)} + b) \geq 1, \forall is.t. y(i)(wTx(i)+b)≥1,∀i
拉格朗日函数:
L(w,b,α)=12∣∣w∣∣2−∑i=1mαi[y(i)(wTx(i)+b)−1]\mathcal{L}(w, b, \alpha) = \frac{1}{2}||w||^2 - \sum_{i=1}^{m} \alpha_i [y^{(i)}(w^T x^{(i)} + b) - 1]L(w,b,α)=21∣∣w∣∣2−i=1∑mαi[y(i)(wTx(i)+b)−1]
KKT条件:
∇wL=w−∑i=1mαiy(i)x(i)=0∂L∂b=−∑i=1mαiy(i)=0αi≥0y(i)(wTx(i)+b)−1≥0αi[y(i)(wTx(i)+b)−1]=0\begin{align} \nabla_w \mathcal{L} &= w - \sum_{i=1}^{m} \alpha_i y^{(i)} x^{(i)} = 0 \\ \frac{\partial \mathcal{L}}{\partial b} &= -\sum_{i=1}^{m} \alpha_i y^{(i)} = 0 \\ \alpha_i &\geq 0 \\ y^{(i)}(w^T x^{(i)} + b) - 1 &\geq 0 \\ \alpha_i [y^{(i)}(w^T x^{(i)} + b) - 1] &= 0 \end{align}∇wL∂b∂Lαiy(i)(wTx(i)+b)−1αi[y(i)(wTx(i)+b)−1]=w−i=1∑mαiy(i)x(i)=0=−i=1∑mαiy(i)=0≥0≥0=0
对偶问题:
maxα∑i=1mαi−12∑i,j=1mαiαjy(i)y(j)⟨x(i),x(j)⟩\max_\alpha \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{m} \alpha_i \alpha_j y^{(i)} y^{(j)} \langle x^{(i)}, x^{(j)} \rangleαmaxi=1∑mαi−21i,j=1∑mαiαjy(i)y(j)⟨x(i),x(j)⟩
s.t. αi≥0,∑i=1mαiy(i)=0\text{s.t. } \alpha_i \geq 0, \sum_{i=1}^{m} \alpha_i y^{(i)} = 0s.t. αi≥0,i=1∑mαiy(i)=0
A.3 K-means聚类的收敛性证明
K-means算法最小化目标函数:
J=∑i=1n∑k=1Krik∣∣xi−μk∣∣2J = \sum_{i=1}^{n} \sum_{k=1}^{K} r_{ik} ||x_i - \mu_k||^2J=i=1∑nk=1∑Krik∣∣xi−μk∣∣2
步骤1:固定μk\mu_kμk,优化rikr_{ik}rik:
rik={1if k=argminj∣∣xi−μj∣∣20otherwiser_{ik} = \begin{cases} 1 & \text{if } k = \arg\min_j ||x_i - \mu_j||^2 \\ 0 & \text{otherwise} \end{cases}rik={10if k=argminj∣∣xi−μj∣∣2otherwise
步骤2:固定rikr_{ik}rik,优化μk\mu_kμk:
∂J∂μk=−2∑i=1nrik(xi−μk)=0\frac{\partial J}{\partial \mu_k} = -2 \sum_{i=1}^{n} r_{ik}(x_i - \mu_k) = 0∂μk∂J=−2i=1∑nrik(xi−μk)=0
解得:
μk=∑i=1nrikxi∑i=1nrik\mu_k = \frac{\sum_{i=1}^{n} r_{ik} x_i}{\sum_{i=1}^{n} r_{ik}}μk=∑i=1nrik∑i=1nrikxi
收敛性:由于每步都减少JJJ且JJJ有下界0,算法必然收敛。
A.4 神经网络反向传播算法推导
对于LLL层神经网络,前向传播:
z(l)=W(l)a(l−1)+b(l)a(l)=g(z(l))\begin{align} z^{(l)} &= W^{(l)} a^{(l-1)} + b^{(l)} \\ a^{(l)} &= g(z^{(l)}) \end{align}z(l)a(l)=W(l)a(l−1)+b(l)=g(z(l))
损失函数:
J=1m∑i=1mL(y(i),a(L)(i))J = \frac{1}{m} \sum_{i=1}^{m} L(y^{(i)}, a^{(L)(i)})J=m1i=1∑mL(y(i),a(L)(i))
反向传播计算梯度:
δ(L)=∇a(L)L⊙g′(z(L))\delta^{(L)} = \nabla_{a^{(L)}} L \odot g'(z^{(L)})δ(L)=∇a(L)L⊙g′(z(L))
对于l=L−1,L−2,...,2l = L-1, L-2, ..., 2l=L−1,L−2,...,2:
δ(l)=(W(l+1))Tδ(l+1)⊙g′(z(l))\delta^{(l)} = (W^{(l+1)})^T \delta^{(l+1)} \odot g'(z^{(l)})δ(l)=(W(l+1))Tδ(l+1)⊙g′(z(l))
权重梯度:
∂J∂W(l)=1mδ(l)(a(l−1))T\frac{\partial J}{\partial W^{(l)}} = \frac{1}{m} \delta^{(l)} (a^{(l-1)})^T∂W(l)∂J=m1δ(l)(a(l−1))T
偏置梯度:
∂J∂b(l)=1m∑iδ(l)(i)\frac{\partial J}{\partial b^{(l)}} = \frac{1}{m} \sum_{i} \delta^{(l)(i)}∂b(l)∂J=m1i∑δ(l)(i)
A.5 LSTM网络的梯度流推导
LSTM的前向传播已在正文给出,这里推导梯度流:
定义顶层梯度:
δt=∂L∂ht\delta_t = \frac{\partial L}{\partial h_t}δt=∂ht∂L
各门梯度:
∂L∂ot=δt⊙tanh(Ct)∂L∂Ct=δt⊙ot⊙(1−tanh2(Ct))+∂L∂Ct+1⊙ft+1∂L∂C~t=∂L∂Ct⊙it∂L∂it=∂L∂Ct⊙C~t∂L∂ft=∂L∂Ct⊙Ct−1\begin{align} \frac{\partial L}{\partial o_t} &= \delta_t \odot \tanh(C_t) \\ \frac{\partial L}{\partial C_t} &= \delta_t \odot o_t \odot (1 - \tanh^2(C_t)) + \frac{\partial L}{\partial C_{t+1}} \odot f_{t+1} \\ \frac{\partial L}{\partial \tilde{C}_t} &= \frac{\partial L}{\partial C_t} \odot i_t \\ \frac{\partial L}{\partial i_t} &= \frac{\partial L}{\partial C_t} \odot \tilde{C}_t \\ \frac{\partial L}{\partial f_t} &= \frac{\partial L}{\partial C_t} \odot C_{t-1} \end{align}∂ot∂L∂Ct∂L∂C~t∂L∂it∂L∂ft∂L=δt⊙tanh(Ct)=δt⊙ot⊙(1−tanh2(Ct))+∂Ct+1∂L⊙ft+1=∂Ct∂L⊙it=∂Ct∂L⊙C~t=∂Ct∂L⊙Ct−1
这种设计使梯度可以通过细胞状态CtC_tCt长距离传播,缓解梯度消失问题。
附录B:投资回报率(ROI)的详细财务模型
B.1 净现值(NPV)计算
AI投资的NPV:
NPV=−I0+∑t=1TCFt(1+r)tNPV = -I_0 + \sum_{t=1}^{T} \frac{CF_t}{(1+r)^t}NPV=−I0+t=1∑T(1+r)tCFt
其中:
- I0I_0I0:初始投资
- CFtCF_tCFt:第ttt期现金流 = (Revenuet−Costt)×(1−tax)+Depreciationt×tax(Revenue_t - Cost_t) \times (1 - tax) + Depreciation_t \times tax(Revenuet−Costt)×(1−tax)+Depreciationt×tax
- rrr:折现率
B.2 内部收益率(IRR)求解
IRR满足方程:
0=−I0+∑t=1TCFt(1+IRR)t0 = -I_0 + \sum_{t=1}^{T} \frac{CF_t}{(1+IRR)^t}0=−I0+t=1∑T(1+IRR)tCFt
使用Newton-Raphson方法迭代求解:
IRRn+1=IRRn−f(IRRn)f′(IRRn)IRR_{n+1} = IRR_n - \frac{f(IRR_n)}{f'(IRR_n)}IRRn+1=IRRn−f′(IRRn)f(IRRn)
其中:
f(IRR)=−I0+∑t=1TCFt(1+IRR)tf(IRR) = -I_0 + \sum_{t=1}^{T} \frac{CF_t}{(1+IRR)^t}f(IRR)=−I0+t=1∑T(1+IRR)tCFt
f′(IRR)=−∑t=1Tt⋅CFt(1+IRR)t+1f'(IRR) = -\sum_{t=1}^{T} \frac{t \cdot CF_t}{(1+IRR)^{t+1}}f′(IRR)=−t=1∑T(1+IRR)t+1t⋅CFt
B.3 投资回收期的概率分布
考虑不确定性,回收期TpT_pTp的概率分布:
P(Tp≤t)=P(∑i=1tCFi≥I0)P(T_p \leq t) = P\left(\sum_{i=1}^{t} CF_i \geq I_0\right)P(Tp≤t)=P(i=1∑tCFi≥I0)
假设现金流服从正态分布CFi∼N(μi,σi2)CF_i \sim N(\mu_i, \sigma_i^2)CFi∼N(μi,σi2),则:
∑i=1tCFi∼N(∑i=1tμi,∑i=1tσi2)\sum_{i=1}^{t} CF_i \sim N\left(\sum_{i=1}^{t} \mu_i, \sum_{i=1}^{t} \sigma_i^2\right)i=1∑tCFi∼N(i=1∑tμi,i=1∑tσi2)
结论:面向未来的中小企业AI战略
本报告通过严格的数学分析和实证数据,证明了AI对中小企业的变革性影响。关键发现包括:
-
量化的商业价值:AI可带来91%的收入增长概率,30%的成本降低,以及每月20+小时的时间节约。
-
指数级市场增长:全球AI市场以29.2%的CAGR增长,从2024年的233.46B233.46B233.46B到2032年的1.77T1.77T1.77T。
-
网络效应和规模收益:AI的价值随采用范围呈超线性增长,V∝n2V \propto n^2V∝n2。
-
风险可管理性:通过适当的框架和控制措施,AI相关风险可以量化和缓解。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容






所有评论(0)