NumPy（Numerical Python）是 Python 科学计算生态系统的核心库，提供了高性能的多维数组对象和用于处理这些数组的工具。如：矩阵数据类型、矢量处理，以及精密的运算库。它是几乎所有数据科学、机器学习和科学计算库的基础。广泛应用于数据分析、机器学习等领域，是 Pandas 、 Scikit-learn 等库的基础。

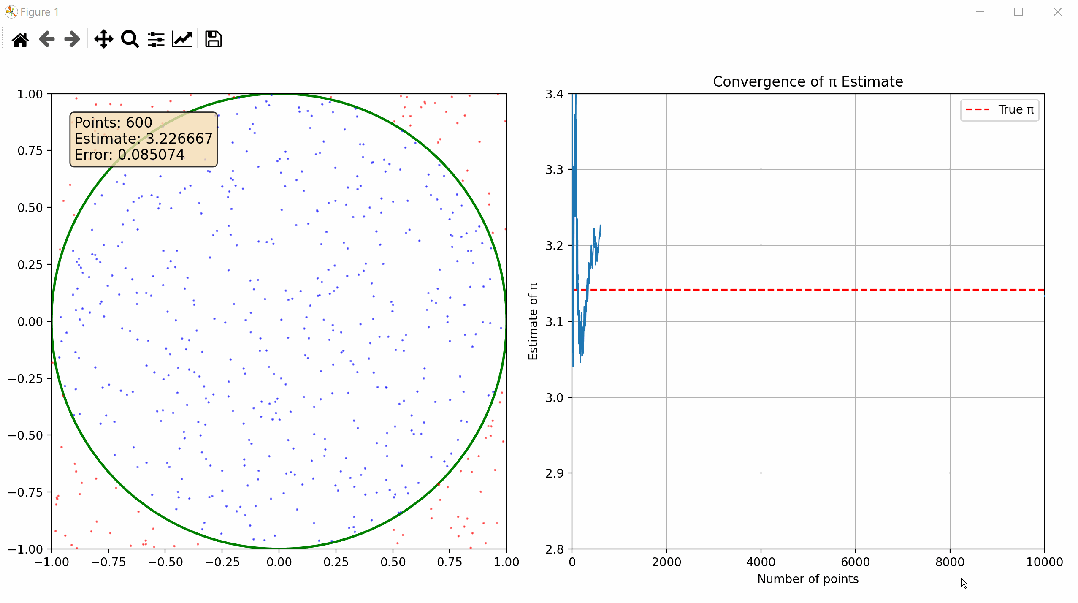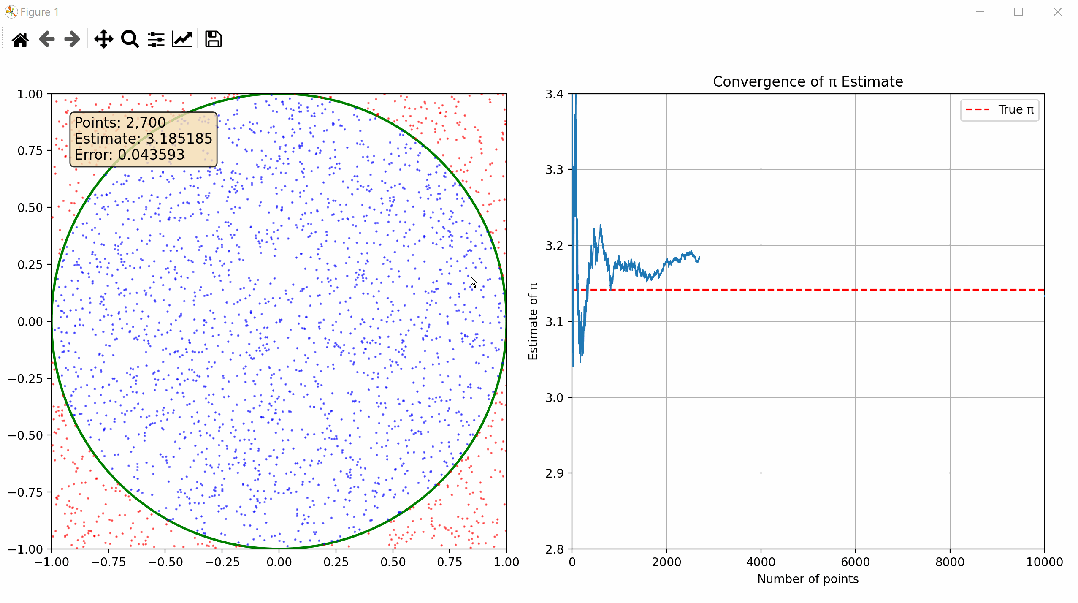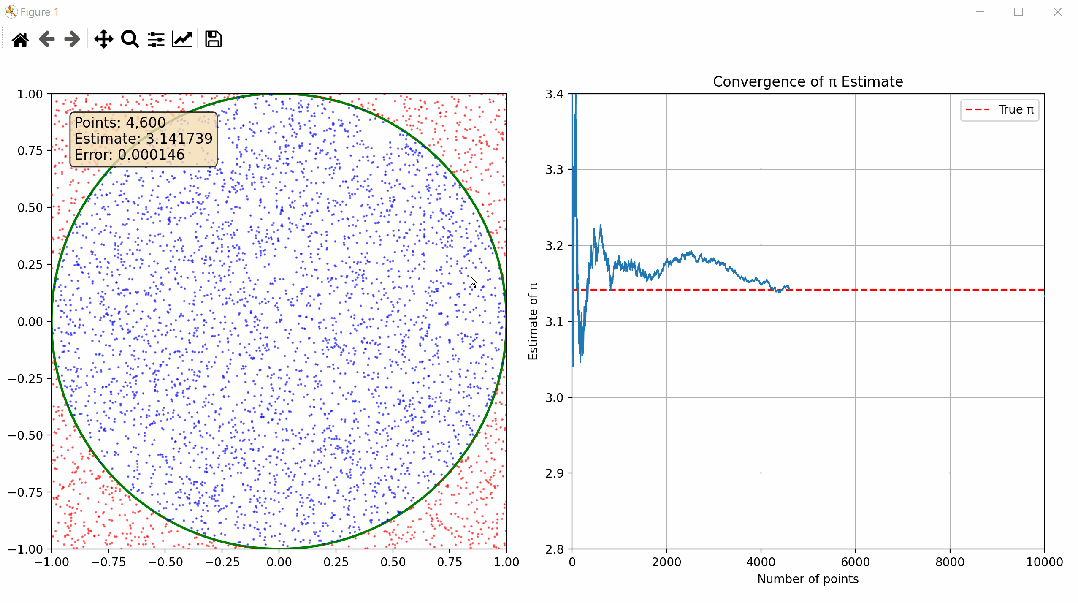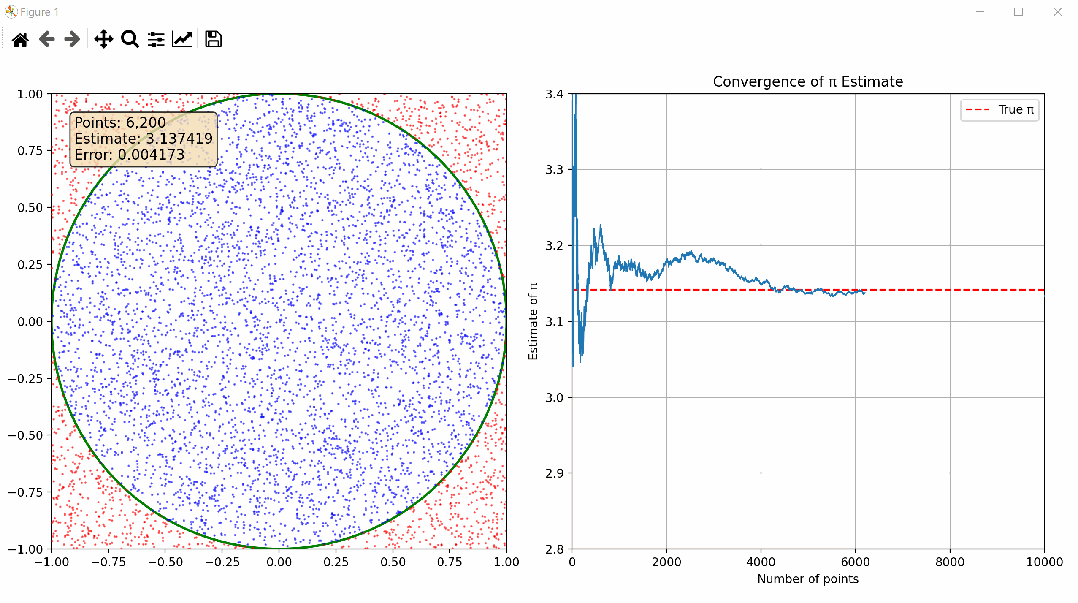
下图是NumPy通过蒙特卡洛方法估算圆周率π，并提供详细的代码实现和可视化，感兴趣可在后文根据详细注解一探究竟；

一、NumPy的优势

1. 与Python 列表的比较

与Python列表的比较，直观体现性能优势：

import numpy as np
import time
# Python 列表的性能问题
python_list = list(range(1000000))
start_time = time.time()
result = [x * 2 for x in python_list]
end_time = time.time()
print(f"Python列表计算时间: {end_time - start_time:.6f}秒")
# NumPy 数组的性能优势
numpy_array = np.arange(1000000)
start_time = time.time()
result = numpy_array * 2
end_time = time.time()
print(f"NumPy数组计算时间: {end_time - start_time:.6f}秒")

结果展示：

Python列表计算时间: 0.045234秒
NumPy数组计算时间: 0.001567秒

2、主要优势

1. 由于底层用 C 语言实现，运算速度极快

2. 数组元素在内存中连续存储，效率极高

3. 向量化操作，避免显式循环，一次操作整个数组

4. 广播机制，处理不同形状的数组之间的逐元素运算

5. 丰富的数学函数、线性代数、随机数生成等

二、由浅入深、循序渐进

1. 核心对象：ndarray

1.1 创建数组

import numpy as np
# 从列表创建
arr1 = np.array([1, 2, 3, 4, 5])
print("从列表创建:", arr1)
# 创建特殊数组
zeros = np.zeros((3, 4))        # 全0数组
ones = np.ones((2, 3))          # 全1数组
empty = np.empty((2, 2))        # 未初始化数组
full = np.full((2, 2), 7)       # 填充指定值
identity = np.eye(3)            # 单位矩阵
print("全0数组:\n", zeros)
print("单位矩阵:\n", identity)
# 创建序列数组
range_arr = np.arange(0, 10, 2)  # 类似range，但返回数组
linear_arr = np.linspace(0, 1, 5)  # 等间隔数列
random_arr = np.random.rand(3, 3)  # 随机数组
print("arange创建:", range_arr)
print("linspace创建:", linear_arr)
print("随机数组:\n", random_arr)

输出结果：​​​​​​

从列表创建: [1 2 3 4 5]
全0数组:
 [[0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]]
单位矩阵:
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
arange创建: [0 2 4 6 8]
linspace创建: [0.   0.25 0.5  0.75 1.  ]
随机数组:
 [[0.39898071 0.38841929 0.25706792]
 [0.4805703  0.79778008 0.96680553]
 [0.75744912 0.35779339 0.96884091]]

1.2 数组属性

import numpy as np
# 创建一个示例数组
arr = np.array([[1, 2, 3], [4, 5, 6]])
print("数组:", arr)
print("形状:", arr.shape)        # 数组维度
print("大小:", arr.size)         # 元素总数
print("维度:", arr.ndim)         # 轴的数量
print("数据类型:", arr.dtype)    # 元素类型
print("每个元素字节数:", arr.itemsize)
print("总字节数:", arr.nbytes)

输出结果：

组: [[1 2 3] [4 5 6]]
形状: (2, 3)
大小: 6
维度: 2
数据类型: int32
每个元素字节数: 4
总字节数: 24

2. 数组操作

2.1 索引和切片

import numpy as np
# 创建示例数组
arr = np.arange(1, 13).reshape(3, 4)
print("原始数组:\n", arr)
# 基本索引
print("第一个元素:", arr[0, 0])
print("第一行:", arr[0])
print("第一列:", arr[:, 0])
# 切片操作
print("前两行:\n", arr[:2])
print("后两列:\n", arr[:, -2:])
print("子数组:\n", arr[1:3, 1:3])
# 布尔索引
bool_mask = arr > 5
print("布尔掩码:\n", bool_mask)
print("大于5的元素:", arr[bool_mask])
# 花式索引
print("选择特定行:", arr[[0, 2]])
print("选择特定列:", arr[:, [1, 3]])

输出结果：

始数组:
 [[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
第一个元素: 1
第一行: [1 2 3 4]
第一列: [1 5 9]
前两行:
 [[1 2 3 4]
 [5 6 7 8]]
后两列:
 [[ 3  4]
 [ 7  8]
 [11 12]]
子数组:
 [[ 6  7]
 [10 11]]
布尔掩码:
 [[False False False False]
 [False  True  True  True]
 [ True  True  True  True]]
大于5的元素: [ 6  7  8  9 10 11 12]
选择特定行: [[ 1  2  3  4]
 [ 9 10 11 12]]
选择特定列: [[ 2  4]
 [ 6  8]
 [10 12]]

2.2 形状操作

import numpy as np
arr = np.arange(12)
print("一维数组:", arr)
# 改变形状
reshaped = arr.reshape(3, 4)
print("重塑为3x4:\n", reshaped)
# 展平数组
flattened = reshaped.flatten()
print("展平:", flattened)
# 转置
transposed = reshaped.T
print("转置:\n", transposed)
# 增加/减少维度
expanded = np.expand_dims(arr, axis=0)
print("增加维度:", expanded.shape)
squeezed = np.squeeze(expanded)
print("压缩维度:", squeezed.shape)

输出结果：

维数组: [ 0  1  2  3  4  5  6  7  8  9 10 11]
重塑为3x4:
 [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
展平: [ 0  1  2  3  4  5  6  7  8  9 10 11]
转置:
 [[ 0  4  8]
 [ 1  5  9]
 [ 2  6 10]
 [ 3  7 11]]
增加维度: (1, 12)
压缩维度: (12,)

3. 数组运算

3.1 数学运算

import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
# 算术运算
print("加法:", a + b)
print("减法:", a - b)
print("乘法:", a * b)    # 元素乘法，不是矩阵乘法
print("除法:", a / b)
print("幂运算:", a ** 2)
# 比较运算
print("相等:", a == b)
print("大于:", a > 2)
# 聚合函数
print("总和:", np.sum(a))
print("均值:", np.mean(a))
print("标准差:", np.std(a))
print("最大值:", np.max(a))
print("最小值:", np.min(a))
# 三角函数
angles = np.array([0, np.pi/2, np.pi])
print("正弦值:", np.sin(angles))

输出结果：

法: [5 7 9]
减法: [-3 -3 -3]
乘法: [ 4 10 18]
除法: [0.25 0.4  0.5 ]
幂运算: [1 4 9]
相等: [False False False]
大于: [False False  True]
总和: 6
均值: 2.0
标准差: 0.816496580927726
最大值: 3
最小值: 1
正弦值: [0.0000000e+00 1.0000000e+00 1.2246468e-16]

3.2 广播机制

import numpy as np
# 标量与数组
arr = np.array([[1, 2, 3], [4, 5, 6]])
print("数组 + 标量:\n", arr + 10)
# 不同形状数组
vector = np.array([10, 20, 30])
print("数组 + 向量:\n", arr + vector)
# 广播规则示例
a = np.array([[1], [2], [3]])  # 形状 (3, 1)
b = np.array([10, 20, 30])     # 形状 (3,)
print("广播加法:\n", a + b)

输出结果：

数组 + 标量:
 [[11 12 13]
 [14 15 16]]
数组 + 向量:
 [[11 22 33]
 [14 25 36]]
广播加法:
 [[11 21 31]
 [12 22 32]
 [13 23 33]]

4. 实用功能

4.1 文件操作

import numpy as np
# 创建示例数据
data = np.random.rand(5, 3)
# 保存到文件
np.savetxt('data.txt', data, delimiter=',')
# 从文件加载
loaded_data = np.loadtxt('data.txt', delimiter=',')
print("从文件加载的数据:\n", loaded_data)
# 二进制格式（更高效）
np.save('data.npy', data)
binary_loaded = np.load('data.npy')
print("二进制加载的数据:\n", binary_loaded)

输出结果：

从文件加载的数据:
 [[0.4553778  0.49906932 0.97523208]
 [0.35906304 0.55012335 0.38348623]
 [0.29169913 0.90129311 0.22774977]
 [0.97325678 0.32749914 0.85698094]
 [0.82758157 0.36911462 0.42524159]]
二进制加载的数据:
 [[0.4553778  0.49906932 0.97523208]
 [0.35906304 0.55012335 0.38348623]
 [0.29169913 0.90129311 0.22774977]
 [0.97325678 0.32749914 0.85698094]
 [0.82758157 0.36911462 0.42524159]]

4.2 随机数生成

import numpy as np
# 设置随机种子（确保可重复性）
np.random.seed(42)
# 生成随机数
uniform = np.random.rand(5)          # [0,1)均匀分布
normal = np.random.randn(5)          # 标准正态分布
integers = np.random.randint(0, 10, 5)  # 随机整数
print("均匀分布:", uniform)
print("正态分布:", normal)
print("随机整数:", integers)
# 随机抽样
choices = np.random.choice(['A', 'B', 'C'], size=10, p=[0.5, 0.3, 0.2])
print("随机选择:", choices)

输出结果：

匀分布: [0.37454012 0.95071431 0.73199394 0.59865848 0.15601864]
正态分布: [ 0.27904129  1.01051528 -0.58087813 -0.52516981 -0.57138017]
随机整数: [5 8 0 9 2]
随机选择: ['A' 'C' 'A' 'C' 'B' 'A' 'A' 'C' 'B' 'A']

5. 基础应用示例

5.1 数据处理

import numpy as np
# 创建示例数据集
data = np.array([
    [1, 2, 3, 4],
    [5, 6, 7, 8],
    [9, 10, 11, 12]
])
# 数据筛选
filtered = data[data > 5]
print("大于5的值:", filtered)
# 条件修改
data[data % 2 == 0] = -1  # 将所有偶数改为-1
print("修改后的数据:\n", data)
# 数据统计
print("每列均值:", np.mean(data, axis=0))
print("每行最大值:", np.max(data, axis=1))

输出结果：

大于5的值: [ 6  7  8  9 10 11 12]
修改后的数据:
 [[ 1 -1  3 -1]
 [ 5 -1  7 -1]
 [ 9 -1 11 -1]]
每列均值: [ 5. -1.  7. -1.]
每行最大值: [ 3  7 11]

5.2 简单图形处理

import numpy as np
# 模拟一个灰度图像（10x10像素）
image = np.random.randint(0, 256, (10, 10))
print("原始图像数据:\n", image)
# 图像处理操作
brightened = np.clip(image + 50, 0, 255)  # 增加亮度
inverted = 255 - image                    # 颜色反转
threshold = (image > 128).astype(int)     # 二值化
print("亮度增强:\n", brightened)
print("颜色反转:\n", inverted)
print("二值化:\n", threshold)

输出结果：

始图像数据:
 [[ 23 218 156  90 149 255 116 104   8  60]
 [ 70  42  74 180 227  17 189  92  11  90]
 [207  61 110 223  21 153  47 136  20 225]
 [  8  93 153  81  81  14 112 107 249  50]
 [160 149  95  60 214 233 149 247 127   7]
 [140 183  32  82 247 128 174  16  44 212]
 [ 34 203 210  89  98  59  48 200 181 111]
 [111  23  99 101 108 130  65 215 123 205]
 [170  93 210  84 230 213  82 126  87 247]
 [187 250   8 157  78  54  54 227  89 164]]
亮度增强:
 [[ 73 255 206 140 199 255 166 154  58 110]
 [120  92 124 230 255  67 239 142  61 140]
 [255 111 160 255  71 203  97 186  70 255]
 [ 58 143 203 131 131  64 162 157 255 100]
 [210 199 145 110 255 255 199 255 177  57]
 [190 233  82 132 255 178 224  66  94 255]
 [ 84 253 255 139 148 109  98 250 231 161]
 [161  73 149 151 158 180 115 255 173 255]
 [220 143 255 134 255 255 132 176 137 255]
 [237 255  58 207 128 104 104 255 139 214]]
颜色反转:
 [[232  37  99 165 106   0 139 151 247 195]
 [185 213 181  75  28 238  66 163 244 165]
 [ 48 194 145  32 234 102 208 119 235  30]
 [247 162 102 174 174 241 143 148   6 205]
 [ 95 106 160 195  41  22 106   8 128 248]
 [115  72 223 173   8 127  81 239 211  43]
 [221  52  45 166 157 196 207  55  74 144]
 [144 232 156 154 147 125 190  40 132  50]
 [ 85 162  45 171  25  42 173 129 168   8]
 [ 68   5 247  98 177 201 201  28 166  91]]
二值化:
 [[0 1 1 0 1 1 0 0 0 0]
 [0 0 0 1 1 0 1 0 0 0]
 [1 0 0 1 0 1 0 1 0 1]
 [0 0 1 0 0 0 0 0 1 0]
 [1 1 0 0 1 1 1 1 0 0]
 [1 1 0 0 1 0 1 0 0 1]
 [0 1 1 0 0 0 0 1 1 0]
 [0 0 0 0 0 1 0 1 0 1]
 [1 0 1 0 1 1 0 0 0 1]
 [1 1 0 1 0 0 0 1 0 1]]

6. 性能调优和错误处理

6.1 性能优化

import numpy as np
# 不好的做法：使用Python循环
def slow_sum(arr):
    result = 0
    for x in arr:
        result += x
    return result
# 好的做法：使用NumPy向量化操作
def fast_sum(arr):
    return np.sum(arr)
# 测试性能
large_arr = np.random.rand(1000000)
import time
start = time.time()
slow_result = slow_sum(large_arr)
end = time.time()
print(f"循环求和: {end - start:.6f}秒")
start = time.time()
fast_result = fast_sum(large_arr)
end = time.time()
print(f"向量化求和: {end - start:.6f}秒")

输出结果：

循环求和: 0.471191秒
向量化求和: 0.003989秒

6.2 常见错误

import numpy as np
# 错误：视图 vs 副本
arr = np.array([1, 2, 3, 4])
view = arr[1:3]    # 这是视图，修改会影响原数组
copy = arr[1:3].copy()  # 这是副本，独立于原数组
view[0] = 999
print("原数组被修改:", arr)  # [1, 999, 3, 4]
copy[0] = 888
print("原数组不变:", arr)    # [1, 999, 3, 4]
# 正确使用数据类型
float_arr = np.array([1, 2, 3], dtype=np.float64)
int_arr = np.array([1.5, 2.7, 3.1], dtype=np.int32)  # 注意会截断
print("浮点数组:", float_arr)
print("整数数组:", int_arr)  # [1, 2, 3]

输出结果：

原数组被修改: [  1 999   3   4]
原数组不变: [  1 999   3   4]
浮点数组: [1. 2. 3.]
整数数组: [1 2 3]

6.3 小结

1. 数组创建：np.array(), np.zeros(), np.ones(), np.arange(), np.linspace()

2. 数组属性：.shape, .dtype, .ndim

3. 索引和切片：基本索引、布尔索引、花式索引

4. 数组操作：reshape(), concatenate(), stack()

5. 数学运算：向量化运算、广播机制

6. 通用函数：np.sin(), np.exp(), np.sqrt()等

7. 线性代数：np.dot(), np.linalg.norm()等

三、趣味示例

1. 井字棋游戏 - 理解二维数组

import numpy as np
# 创建游戏棋盘
def create_board():
    """
    创建一个3x3的井字棋棋盘，初始状态为全0
    返回值: 3x3的NumPy数组，数据类型为整数
    0表示空位，1表示玩家X，2表示玩家O
    """
    # np.zeros((3, 3), dtype=int) 创建一个3行3列的全0数组
    return np.zeros((3, 3), dtype=int)
# 打印棋盘（美化输出）
def print_board(board):
    """
    将数字表示的棋盘转换为可视化的字符格式并打印
    参数:
    board: 3x3的NumPy数组，表示当前棋盘状态
    """
    # 定义数字到符号的映射字典
    # 0 -> 空格, 1 -> 'X', 2 -> 'O'
    symbols = {0: ' ', 1: 'X', 2: 'O'}
    # 遍历每一行
    for i in range(3):
        # 将当前行的数字转换为对应的符号
        row = [symbols[board[i, j]] for j in range(3)]
        # 使用' | '连接符号并打印，前面加空格使输出居中
        print(' ' + ' | '.join(row))
        # 如果不是最后一行，打印分隔线
        if i < 2:
            print('-----------')
    print()  # 打印空行使输出更清晰
# 检查胜利条件
def check_win(board, player):
    """
    检查指定玩家是否获胜
    参数:
    board: 3x3的NumPy数组，表示当前棋盘状态
    player: 整数，1表示玩家X，2表示玩家O
    返回值:
    布尔值，True表示该玩家获胜，False表示未获胜
    """
    # 检查所有行是否有获胜情况
    # np.all() 检查给定轴上的所有元素是否为True
    for i in range(3):
        # 检查第i行是否全部由当前玩家的棋子占据
        if np.all(board[i, :] == player):
            return True
    # 检查所有列是否有获胜情况
    for j in range(3):
        # 检查第j列是否全部由当前玩家的棋子占据
        if np.all(board[:, j] == player):
            return True
    # 检查两条对角线是否有获胜情况
    # np.diag() 获取矩阵的主对角线元素
    # np.fliplr() 左右翻转矩阵，然后获取对角线即为反对角线
    if np.all(np.diag(board) == player) or np.all(np.diag(np.fliplr(board)) == player):
        return True
    # 如果以上条件都不满足，则该玩家未获胜
    return False
# 游戏演示
# 创建初始棋盘
board = create_board()
print("初始棋盘:")
print_board(board)
# 模拟几步游戏
# 玩家X在左上角(0,0)位置落子
board[0, 0] = 1  # X 在左上角
# 玩家O在中心(1,1)位置落子
board[1, 1] = 2  # O 在中心
# 玩家X在上中(0,1)位置落子
board[0, 1] = 1  # X 在上中
print("游戏进行中:")
print_board(board)
# 检查玩家X是否获胜
print("X 是否获胜?", check_win(board, 1))

输出结果：

初始棋盘:
   |   |  
-----------
   |   |
-----------
   |   |
游戏进行中:
 X | X |
-----------
   | O |
-----------
   |   |
X 是否获胜? False

体现的知识点

• np.zeros() 创建数组

• 二维数组索引 board[i, j]

• np.all() 检查所有元素是否满足条件

• np.diag() 获取对角线元素

• np.fliplr() 左右翻转数组

2. 蒙特卡洛方法估算π的动态可视化

import numpy as np
import matplotlib.pyplot as plt
import time
from matplotlib.animation import FuncAnimation
def animated_monte_carlo(n_samples=10000, frame_interval=100):
    """
    创建蒙特卡洛方法估算π的动态可视化
    参数:
    n_samples: 总采样点数，默认10000个点
    frame_interval: 每帧更新的点数，默认每100个点更新一次动画
    返回:
    matplotlib.animation.FuncAnimation对象，用于控制动画
    """
    # 生成所有随机点：在[-1, 1] x [-1, 1]的正方形区域内均匀采样
    # points是一个n_samples x 2的数组，每行代表一个点的(x,y)坐标
    points = np.random.uniform(-1, 1, size=(n_samples, 2))
    # 计算每个点到原点(0,0)的距离
    # 使用欧几里得距离公式：sqrt(x² + y²)
    distances = np.sqrt(points[:, 0]**2 + points[:, 1]**2)
    # 创建图形窗口，包含左右两个子图
    # 左图显示随机点和单位圆，右图显示π估计值的收敛过程
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
    # 初始化左图的散点图（开始时没有点）
    scatter = ax1.scatter([], [], s=1, alpha=0.5)  # 小点，半透明
    ax1.set_xlim(-1, 1)    # 设置x轴范围
    ax1.set_ylim(-1, 1)    # 设置y轴范围
    ax1.set_aspect('equal') # 保持纵横比相等，确保圆看起来是圆形
    # 在左图绘制单位圆（半径为1的圆）
    # 这个圆用于可视化：圆内的点表示落在单位圆内
    circle = plt.Circle((0, 0), 1, color='green', fill=False, linewidth=2)
    ax1.add_patch(circle)  # 将圆添加到图中
    # 初始化右图的收敛曲线（开始时没有数据）
    line, = ax2.plot([], [], linewidth=1)
    # 在右图添加一条水平线表示π的真实值
    ax2.axhline(y=np.pi, color='r', linestyle='--', label='True π')
    ax2.set_xlim(0, n_samples)  # 设置x轴范围（点数）
    ax2.set_ylim(2.8, 3.4)      # 设置y轴范围（π的估计值范围）
    ax2.set_xlabel('Number of points')    # x轴标签
    ax2.set_ylabel('Estimate of π')       # y轴标签
    ax2.set_title('Convergence of π Estimate')  # 右图标题
    ax2.legend()    # 显示图例
    ax2.grid(True)  # 显示网格
    # 在左图添加文本框，显示当前点数、π估计值和误差
    text = ax1.text(0.05, 0.95, '', transform=ax1.transAxes, fontsize=12,
                   verticalalignment='top', bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.8))
    # 动画更新函数 - 每一帧调用一次
    def update(frame):
        # 计算当前帧应该显示的点数
        # 每frame_interval个点更新一次，但不超过总点数n_samples
        n = min((frame + 1) * frame_interval, n_samples)
        # 更新左图的散点图
        # 确定哪些点落在单位圆内（距离<=1）
        inside = distances[:n] <= 1
        # 落在圆外的点
        outside = ~inside  # 逻辑非操作
        # 创建颜色数组：圆内的点为蓝色，圆外的点为红色
        colors = np.empty(n, dtype=object)  # 创建空对象数组
        colors[inside] = 'blue'   # 圆内的点设为蓝色
        colors[outside] = 'red'   # 圆外的点设为红色
        # 更新散点图的位置和颜色
        scatter.set_offsets(points[:n])  # 设置点的位置
        scatter.set_color(colors)        # 设置点的颜色
        # 更新右图的收敛曲线
        # 计算累积落在圆内的点数（使用累积和）
        cumulative_inside = np.cumsum(inside)
        # 计算π的估计值：4 * (圆内点数 / 总点数)
        # 根据公式：π ≈ 4 * (圆内点数 / 总点数)
        cumulative_estimate = 4 * cumulative_inside / (np.arange(n) + 1)
        # 更新收敛曲线的数据
        line.set_data(np.arange(n), cumulative_estimate)
        # 更新文本信息
        # 获取当前的π估计值（最后一个值）
        current_estimate = cumulative_estimate[-1] if n > 0 else 0
        # 设置文本内容：点数、估计值和误差
        text.set_text(f'Points: {n:,}\nEstimate: {current_estimate:.6f}\nError: {abs(current_estimate - np.pi):.6f}')
        # 返回需要更新的图形元素
        return scatter, line, text
    # 计算总帧数：总点数除以每帧更新的点数
    frames = n_samples // frame_interval
    # 创建动画对象
    # fig: 动画所在的图形
    # update: 更新函数
    # frames: 总帧数
    # interval: 帧间隔时间（毫秒）
    # blit: 使用blitting技术优化动画（只重绘变化的部分）
    ani = FuncAnimation(fig, update, frames=frames, interval=50, blit=True)
    # 调整子图布局，避免重叠
    plt.tight_layout()
    # 显示动画
    plt.show()
    # 返回动画对象，以便后续控制（如保存为视频）
    return ani
# 运行动画
# 使用10000个点，每100个点更新一次动画
ani = animated_monte_carlo(n_samples=10000, frame_interval=100)

• 基本原理

这段代码实现了使用蒙特卡洛方法估算π值的动态可视化，其数学原理如下：

1. 基本思想：在一个边长为2的正方形内随机撒点，统计落在内切圆（半径为1）内的点数

2. 面积关系：

   • 正方形面积 = 2 × 2 = 4

   • 圆形面积 = π × 1² = π

3. 概率估计：点在圆内的概率 = 圆形面积 / 正方形面积 = π/4

4. π估算公式：π ≈ 4 × (圆内点数 / 总点数)

• 代码亮点解析

1. 向量化计算：使用NumPy一次性生成所有随机点并计算距离，避免了低效的Python循环

2. 动态可视化：使用Matplotlib的动画功能实时展示估算过程

3. 双视图设计：左侧显示随机点分布，右侧显示π估计值的收敛过程

4. 性能优化：

   • 使用blit=True只重绘变化的部分，提高动画性能

   • 分批更新点（每100个点更新一次），平衡视觉效果和性能

5. 信息丰富：实时显示当前点数、π估计值和误差，方便观察收敛过程

3. 图像滤镜 - 理解数组运算

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
# 设置中文字体支持
# 确保图表中的中文标题能够正确显示
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体显示中文
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
# 创建简单的测试图像
def create_test_image():
    """
    创建一个自定义的渐变测试图像，用于演示图像处理效果
    返回:
    一个100x100像素的RGB图像，数据类型为uint8（0-255范围）
    """
    # 创建从0到1的等间距数组，用于x和y坐标
    x = np.linspace(0, 1, 100)  # 100个点，从0到1
    y = np.linspace(0, 1, 100)  # 100个点，从0到1
    # 创建网格坐标矩阵
    # xx的每一行都是x的复制，yy的每一列都是y的复制
    xx, yy = np.meshgrid(x, y)
    # 创建RGB三个通道的渐变效果
    red = xx        # 红色通道：水平渐变（从左到右增强）
    green = yy      # 绿色通道：垂直渐变（从下到上增强）
    blue = (xx + yy) / 2  # 蓝色通道：对角线渐变（从右下到左上增强）
    # 将三个通道堆叠成三维数组（高度×宽度×通道）
    # 然后缩放到0-255范围并转换为8位无符号整数
    image = np.stack([red, green, blue], axis=2)
    return (image * 255).astype(np.uint8)
# 定义彩虹色条纹的颜色值（RGB格式，范围0-1）
colors = [
    [1, 0, 0],    # 红色
    [1, 0.5, 0],  # 橙色
    [1, 1, 0],    # 黄色
    [0, 1, 0],    # 绿色
    [0, 0, 1],    # 蓝色
    [0.5, 0, 0.5],# 紫色
]
# 创建彩虹色条纹图像
def create_rainbow_stripes(size=100):
    """
    创建一个彩虹色条纹图像
    参数:
    size: 图像的大小（将创建size×size的正方形图像）
    返回:
    一个包含彩虹色条纹的RGB图像
    """
    # 创建一个全零的三维数组（高度×宽度×3个颜色通道）
    image = np.zeros((size, size, 3))
    # 计算每个条纹的宽度（将图像水平分成6等份）
    stripe_width = size // len(colors)
    # 填充彩虹色条纹
    for i, color in enumerate(colors):
        # 计算当前条纹的起始和结束列索引
        start = i * stripe_width
        end = (i + 1) * stripe_width if i < len(colors) - 1 else size
        # 将当前条纹的所有行和指定列范围设置为当前颜色
        image[:, start:end] = color
    return image
# 应用各种滤镜
def apply_filters(image):
    """
    对输入图像应用多种滤镜效果
    参数:
    image: 输入图像（NumPy数组，uint8类型，0-255范围）
    返回:
    四个处理后的图像：灰度图、边缘检测图、颜色反转图、sepia色调图
    """
    # 将图像转换为浮点数并归一化到0-1范围，便于数学运算
    img_float = image.astype(float) / 255.0
    # 1. 灰度化：将彩色图像转换为灰度图像
    # 方法：取RGB三个通道的平均值
    gray = np.mean(img_float, axis=2)
    # 2. 边缘检测（使用简化的Sobel算子）
    # 定义Sobel算子的x方向和y方向卷积核
    sobel_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])  # 水平边缘检测
    sobel_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])  # 垂直边缘检测
    # 初始化边缘强度图
    edges = np.zeros_like(gray)
    # 对每个颜色通道分别应用Sobel算子
    for i in range(3):
        # 获取当前颜色通道
        channel = img_float[:, :, i]
        # 使用卷积计算x方向和y方向的梯度
        # 注意：这里使用了一维卷积，需要先将二维数组展平
        gx = np.abs(np.convolve(channel.flatten(), sobel_x.flatten(), mode='same').reshape(channel.shape))
        gy = np.abs(np.convolve(channel.flatten(), sobel_y.flatten(), mode='same').reshape(channel.shape))
        # 计算梯度幅值并累加到边缘图中
        edges += np.sqrt(gx**2 + gy**2)
    # 对三个通道的结果取平均
    edges = edges / 3.0
    # 3. 颜色反转：用1减去每个像素值，实现颜色反转效果
    inverted = 1.0 - img_float
    # 4. Sepia色调（棕褐色调效果）
    # 定义Sepia色调的转换矩阵
    sepia_matrix = np.array([[0.393, 0.769, 0.189],   # 红色分量转换系数
                           [0.349, 0.686, 0.168],     # 绿色分量转换系数
                           [0.272, 0.534, 0.131]])    # 蓝色分量转换系数
    # 应用矩阵乘法实现颜色转换
    sepia = np.dot(img_float, sepia_matrix.T)
    # 确保值在0-1范围内（使用np.clip防止溢出）
    sepia = np.clip(sepia, 0, 1)
    return gray, edges, inverted, sepia
# 创建并处理图像
# 生成测试图像
image = create_test_image()
# 应用各种滤镜
gray, edges, inverted, sepia = apply_filters(image)
# 创建彩虹色条纹图像
rainbow_image = create_rainbow_stripes()
# 显示结果
# 创建2行3列的子图布局
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
# 第一行第一列：原始图像
axes[0, 0].imshow(image)
axes[0, 0].set_title('原始图像')
axes[0, 0].axis('off')  # 隐藏坐标轴
# 第一行第二列：灰度化效果
axes[0, 1].imshow(gray, cmap='gray')  # 使用灰度颜色映射
axes[0, 1].set_title('灰度化')
axes[0, 1].axis('off')
# 第一行第三列：边缘检测效果
axes[0, 2].imshow(edges, cmap='hot')  # 使用热力图颜色映射
axes[0, 2].set_title('边缘检测')
axes[0, 2].axis('off')
# 第二行第一列：颜色反转效果
axes[1, 0].imshow(inverted)
axes[1, 0].set_title('颜色反转')
axes[1, 0].axis('off')
# 第二行第二列：Sepia色调效果
axes[1, 1].imshow(sepia)
axes[1, 1].set_title('Sepia色调')
axes[1, 1].axis('off')
# 第二行第三列：彩虹条纹图像
axes[1, 2].imshow(rainbow_image)
axes[1, 2].set_title('彩虹条纹')
axes[1, 2].axis('off')
# 自动调整子图参数，使之填充整个图像区域
plt.tight_layout()
# 显示图形
plt.show()

体现的知识点

• 数组创建和形状操作

• 数学运算和广播

• 数组索引和切片

• np.convolve() 卷积操作

• np.clip() 限制数值范围

• np.dot() 矩阵乘法

代码技术亮点

• 数组操作: 使用np.linspace, np.meshgrid创建坐标网格

• 广播机制: 在创建渐变图像时利用了NumPy的广播功能

• 矩阵运算: 在Sepia滤镜中使用矩阵乘法实现颜色转换

• 卷积操作: 在边缘检测中使用卷积计算图像梯度

• 数组索引和切片: 在创建彩虹条纹时使用切片操作高效赋值

四、总结

操作	代码示例	说明
创建数组	np.array([1,2,3])	从列表创建
全零数组	np.zeros((3,3))	创建全0数组
全一数组	np.ones((2,2))	创建全1数组
范围数组	np.arange(0,10,2)	创建等差数组
随机数组	np.random.rand(3,3)	创建随机数组
改变形状	arr.reshape(2,3)	改变数组形状
数组拼接	np.concatenate([a,b])	连接数组
数学运算	arr + 1, arr * 2	向量化运算
统计函数	np.mean(arr), np.std(arr)	统计计算