人工智能与世界模型# 系列文章目录

第一章 数学基础（一）导数、偏导数、方向导数与梯度
第二章 数学基础（二）向量、矩阵、行列式与线性变换
第三章 机器学习中的Hello World：线性回归（一）
第四章 机器学习中的Hello World：线性回归（二）
第五章 优化算法进阶：从梯度下降到随机梯度下降（SGD）与批量梯度下降（BGD）
第六章 分类问题的基石：逻辑回归（Logistic Regression）

---

---

前言

在前面的章节中，我们已经掌握了：

1. 数学基础：导数、梯度、向量、矩阵。
2. 回归问题：使用线性回归预测连续值（如房价）。
3. 优化方法：使用梯度下降及其变体（SGD/MBGD）来高效地求解模型参数。

然而，现实世界中的问题远不止“预测一个数值”这么简单。我们更常遇到的是分类问题：

• 判断一封邮件是垃圾邮件还是非垃圾邮件（二分类）。
• 识别一张图片是猫、狗还是鸟（多分类）。
• 预测用户是否会点击某个广告（二分类）。

本章，我们将介绍机器学习中处理分类问题的“Hello World”——逻辑回归（Logistic Regression）。它虽然名字里有“回归”，但本质上是一个强大的分类模型，更是通往神经网络世界的关键一步。

---

一、从线性回归到逻辑回归：引入非线性

1.1 线性回归的局限性

在线性回归中，我们的模型输出 $\hat{y}$ 是一个连续值：
$$\hat{y}={\mathbf{W}}^T\mathbf{X}+b$$
这个输出 $\hat{y}$ 的范围是 $(-\infty ,+\infty )$。如果我们要用它来解决分类问题，比如预测“是否点击广告”（结果只有 0 或 1），就会遇到问题：

1. 输出范围不匹配：我们希望输出是概率（0 到 1 之间），但线性回归的输出可能远超 1 或低于 0。
2. 硬性分类困难：如果简单地设定 $\hat{y}>0.5$ 为 1，$\hat{y}\le 0.5$ 为 0，那么一个极端的 $\hat{y}=100$ 和一个 $\hat{y}=0.6$ 在分类上没有区别，但在模型中却代表了巨大的误差，这会使得模型对异常值非常敏感。

1.2 引入 Sigmoid 函数（激活函数）

为了将线性模型的输出压缩到 $(0,1)$ 之间，使其具有概率意义，我们引入了一个特殊的非线性函数——Sigmoid 函数（也称逻辑函数）。

$$g(z)=\frac{1}{1+e^{-z}}$$

其中，$z={\mathbf{W}}^T\mathbf{X}+b$ 是线性回归的输出。

Sigmoid 函数的特性：

• 范围：将任意实数 $z$ 映射到 $(0,1)$ 之间。
• 非线性：引入了非线性因素，使得模型能够处理非线性决策边界。
• 概率解释：输出 $h(\mathbf{X})=g(z)$ 可以被解释为样本 $\mathbf{X}$ 属于正类别（$y=1$）的概率：
  $$P(y=1|\mathbf{X};\mathbf{W},b)=h(\mathbf{X})$$

1.3 逻辑回归的模型

逻辑回归的模型可以表示为：
$$h(\mathbf{X})=\frac{1}{1+e^{-({\mathbf{W}}^T\mathbf{X}+b)}}$$
我们的目标是找到最优的参数 $\mathbf{W}$ 和 $b$，使得这个概率 $h(\mathbf{X})$ 能够最好地拟合训练数据中的真实标签 $y$。

---

二、逻辑回归的损失函数：交叉熵（Cross-Entropy）

在线性回归中，我们使用均方误差（MSE）作为损失函数。但如果我们将 Sigmoid 函数的输出代入 MSE，得到的损失函数将是非凸的，这意味着它有很多局部最小值，梯度下降算法很容易陷入其中，无法找到全局最优解。

因此，我们需要为逻辑回归设计一个更合适的损失函数——交叉熵损失（Cross-Entropy Loss），也称为对数损失（Log Loss）。

2.1 交叉熵损失的定义

对于单个样本 $(\mathbf{X},y)$，其损失函数 $L(\mathbf{W})$ 定义为：

$$L(\mathbf{W})=-[y\log (h(\mathbf{X}))+(1-y)\log (1-h(\mathbf{X}))]$$

其中 $y$ 是真实标签（0 或 1），$h(\mathbf{X})$ 是模型预测的概率。

2.2 损失函数的几何意义（为什么是它？）

这个损失函数非常巧妙地利用了 $y$ 只能取 0 或 1 的特性：

1. 当真实标签 $y=1$ 时：
   $$L(\mathbf{W})=-[1\cdot \log (h(\mathbf{X}))+(1-1)\cdot \log (1-h(\mathbf{X}))]=-\log (h(\mathbf{X}))$$

   • 如果模型预测 $h(\mathbf{X})\to 1$（正确），则 $L(\mathbf{W})\to -\log (1)=0$（损失很小）。
   • 如果模型预测 $h(\mathbf{X})\to 0$（错误），则 $L(\mathbf{W})\to -\log (0)=\infty$（损失巨大）。

2. 当真实标签 $y=0$ 时：
   $$L(\mathbf{W})=-[0\cdot \log (h(\mathbf{X}))+(1-0)\cdot \log (1-h(\mathbf{X}))]=-\log (1-h(\mathbf{X}))$$

   • 如果模型预测 $h(\mathbf{X})\to 0$（正确），则 $L(\mathbf{W})\to -\log (1)=0$（损失很小）。
   • 如果模型预测 $h(\mathbf{X})\to 1$（错误），则 $L(\mathbf{W})\to -\log (0)=\infty$（损失巨大）。

总结：交叉熵损失函数能够完美地惩罚错误的预测，并且它是一个凸函数（对于逻辑回归而言），保证了我们可以使用梯度下降法找到全局最优解。

2.3 整体损失函数

对于 $m$ 个样本的训练集，整体损失函数（平均损失）为：
$$J(\mathbf{W})=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log (h({\mathbf{X}}^{(i)}))+(1-y^{(i)})\log (1-h({\mathbf{X}}^{(i)}))]$$

---

三、梯度下降求解：神奇的巧合

我们的优化目标是：
$${\mathbf{W}}^{\ast }=\arg \underset{\mathbf{W}}{\min }J(\mathbf{W})$$
和线性回归一样，我们使用梯度下降法来求解。

3.1 梯度的计算

对 $J(\mathbf{W})$ 求偏导，得到梯度 $\nabla J(\mathbf{W})$。

令人惊奇的是，尽管逻辑回归的模型和损失函数看起来比线性回归复杂得多，但最终推导出的梯度形式却出奇地简洁：

$$\frac{\partial J(\mathbf{W})}{\partial \mathbf{W}}=\frac{1}{m}\sum _{i=1}^m({\mathbf{X}}^{(i)}(h({\mathbf{X}}^{(i)})-y^{(i)}))$$

对比线性回归的梯度：
$$\frac{\partial L(\mathbf{W})}{\partial \mathbf{W}}=\frac{1}{m}\sum _{i=1}^m({\mathbf{X}}^{(i)}({\hat{y}}^{(i)}-y^{(i)}))$$

你会发现，逻辑回归的梯度形式与线性回归的梯度形式是完全一样的！ 唯一的区别在于：

• 线性回归中的 ${\hat{y}}^{(i)}$ 是线性输出 ${\mathbf{W}}^T{\mathbf{X}}^{(i)}+b$。
• 逻辑回归中的 $h({\mathbf{X}}^{(i)})$ 是经过 Sigmoid 函数处理后的概率 $\frac{1}{1+e^{-({\mathbf{W}}^T{\mathbf{X}}^{(i)}+b)}}$。

3.2 参数更新

有了梯度，我们就可以使用第五章学到的**小批量梯度下降（MBGD）**来更新参数：

$${\mathbf{W}}_{\text{new}}={\mathbf{W}}_{\text{old}}-\alpha \nabla J(\mathbf{W})$$

---

四、逻辑回归的工程实践与局限性

4.1 实践：多分类问题（Softmax）

逻辑回归本身是二分类模型。如果我们需要处理多分类问题（如识别猫、狗、鸟），我们可以将 Sigmoid 函数替换为 Softmax 函数，并将交叉熵损失推广为多类别交叉熵损失。

Softmax 函数将模型的输出转化为一个概率分布，即所有类别的概率之和为 1。

对于 $K$ 个类别，模型会输出 $K$ 个分数 $z_1,z_2,\dots ,z_K$。Softmax 函数将这些分数转换为概率 $p_i$：
$$p_i=\frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_j}}$$
其中，分子 $e^{z_i}$ 确保了概率为正，分母 ${\sum }_{j=1}^K{e}^{z_j}$ 确保了所有概率之和为 1。Softmax 函数是多分类问题中，将线性输出转化为概率的标准激活函数。

4.2 局限性：线性决策边界

逻辑回归的本质仍然是线性模型。它只能找到一个线性决策边界（一条直线或一个平面）来分隔不同类别的样本。

如果数据是线性可分的，逻辑回归表现优秀。
如果数据是线性不可分的，逻辑回归将无能为力。

如何解决线性不可分问题？

1. 特征工程：手动创建非线性特征（如 $x_1^2,x_1{x}_2$），将数据映射到高维空间使其线性可分。
2. 引入多层非线性结构：将多个逻辑回归模型堆叠起来，形成一个多层感知机（Multi-Layer Perceptron, MLP），也就是我们下一章要正式进入的神经网络。

五、代码实现

5.1 手写逻辑回归

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

# ----------------------------------------------------------------------
# 1. 数据生成
# ----------------------------------------------------------------------
def create_data():
    # 生成一个线性可分的数据集
    X, y = make_classification(
        n_samples=100, 
        n_features=2, 
        n_informative=2, 
        n_redundant=0, 
        n_classes=2, 
        n_clusters_per_class=1, 
        flip_y=0.1, 
        random_state=42
    )
    # 将 y 转换为 (m, 1) 的列向量
    y = y.reshape(-1, 1)
    return X, y

# ----------------------------------------------------------------------
# 2. 逻辑回归模型 (手写实现)
# ----------------------------------------------------------------------
class LogisticRegressionHandwritten:
    def __init__(self, learning_rate=0.01, epochs=1000):
        self.learning_rate = learning_rate
        self.epochs = epochs
        self.W = None  # 权重 (n_features + 1, 1)
        self.loss_history = []

    def _sigmoid(self, z):
        # Sigmoid 激活函数
        return 1 / (1 + np.exp(-z))

    def _add_bias(self, X):
        # 在特征矩阵 X 的第一列添加偏置项 x0=1
        m = X.shape[0]
        return np.hstack((np.ones((m, 1)), X))

    def fit(self, X, y):
        # 准备数据
        X_b = self._add_bias(X)  # (m, n+1)
        m, n = X_b.shape
        
        # 初始化权重 W (n+1, 1)
        # 使用 Xavier/Glorot 初始化，防止梯度消失/爆炸，这里简化为小随机数
        self.W = np.random.randn(n, 1) * 0.01
        
        # 梯度下降训练
        for epoch in range(self.epochs):
            # 1. 线性输出 (m, 1)
            z = np.dot(X_b, self.W)
            
            # 2. 预测概率 (m, 1)
            h = self._sigmoid(z)
            
            # 3. 计算损失 (交叉熵损失)
            # J(W) = - (1/m) * sum[y*log(h) + (1-y)*log(1-h)]
            # 避免 log(0) 错误，使用极小值 epsilon
            epsilon = 1e-15
            loss = - (1/m) * np.sum(y * np.log(h + epsilon) + (1 - y) * np.log(1 - h + epsilon))
            self.loss_history.append(loss)
            
            # 4. 计算梯度 (n+1, 1)
            # 梯度形式与线性回归一致: (1/m) * X_b.T * (h - y)
            gradient = (1/m) * np.dot(X_b.T, (h - y))
            
            # 5. 更新权重
            self.W = self.W - self.learning_rate * gradient
            
            # 打印进度
            if (epoch + 1) % 100 == 0:
                print(f"Epoch {epoch+1}/{self.epochs}, Loss: {loss:.4f}")

    def predict_proba(self, X):
        # 预测概率
        X_b = self._add_bias(X)
        z = np.dot(X_b, self.W)
        return self._sigmoid(z)

    def predict(self, X, threshold=0.5):
        # 预测类别 (0 或 1)
        probabilities = self.predict_proba(X)
        return (probabilities >= threshold).astype(int)

# ----------------------------------------------------------------------
# 3. 可视化函数
# ----------------------------------------------------------------------
def plot_results(model, X, y, title):
    # 绘制数据点和决策边界
    plt.figure(figsize=(10, 6))
    
    # 绘制数据点
    plt.scatter(X[:, 0], X[:, 1], c=y.flatten(), cmap=plt.cm.RdYlBu, marker='o', edgecolors='k')
    
    # 绘制决策边界
    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                         np.arange(y_min, y_max, 0.02))
    
    # 预测网格点的类别
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    # 绘制等高线图
    plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlBu)
    
    plt.title(title)
    plt.xlabel("Feature 1")
    plt.ylabel("Feature 2")
    plt.colorbar(label='Predicted Class')
    plt.grid(True, linestyle='--', alpha=0.6)
    
    # 保存决策边界图
    plt.savefig(f"{title.replace(' ', '_')}_decision_boundary.png")
    plt.close()

def plot_loss(loss_history, title):
    # 绘制损失下降曲线
    plt.figure(figsize=(10, 6))
    plt.plot(loss_history, label='Loss (Cross-Entropy)')
    plt.title(title)
    plt.xlabel("Epoch")
    plt.ylabel("Loss")
    plt.grid(True, linestyle='--', alpha=0.6)
    plt.legend()
    
    # 保存损失曲线图
    plt.savefig(f"{title.replace(' ', '_')}_loss_curve.png")
    plt.close()

# ----------------------------------------------------------------------
# 4. 运行手写模型
# ----------------------------------------------------------------------
if __name__ == "__main__":
    # 1. 准备数据
    X, y = create_data()
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
    
    # 2. 训练模型
    lr_handwritten = LogisticRegressionHandwritten(learning_rate=0.1, epochs=1000)
    print("--- 开始训练手写逻辑回归模型 ---")
    lr_handwritten.fit(X_train, y_train)
    print("--- 训练完成 ---")
    
    # 3. 评估模型
    y_pred_test = lr_handwritten.predict(X_test)
    accuracy = np.mean(y_pred_test == y_test)
    print(f"测试集准确率: {accuracy * 100:.2f}%")
    
    # 4. 可视化结果
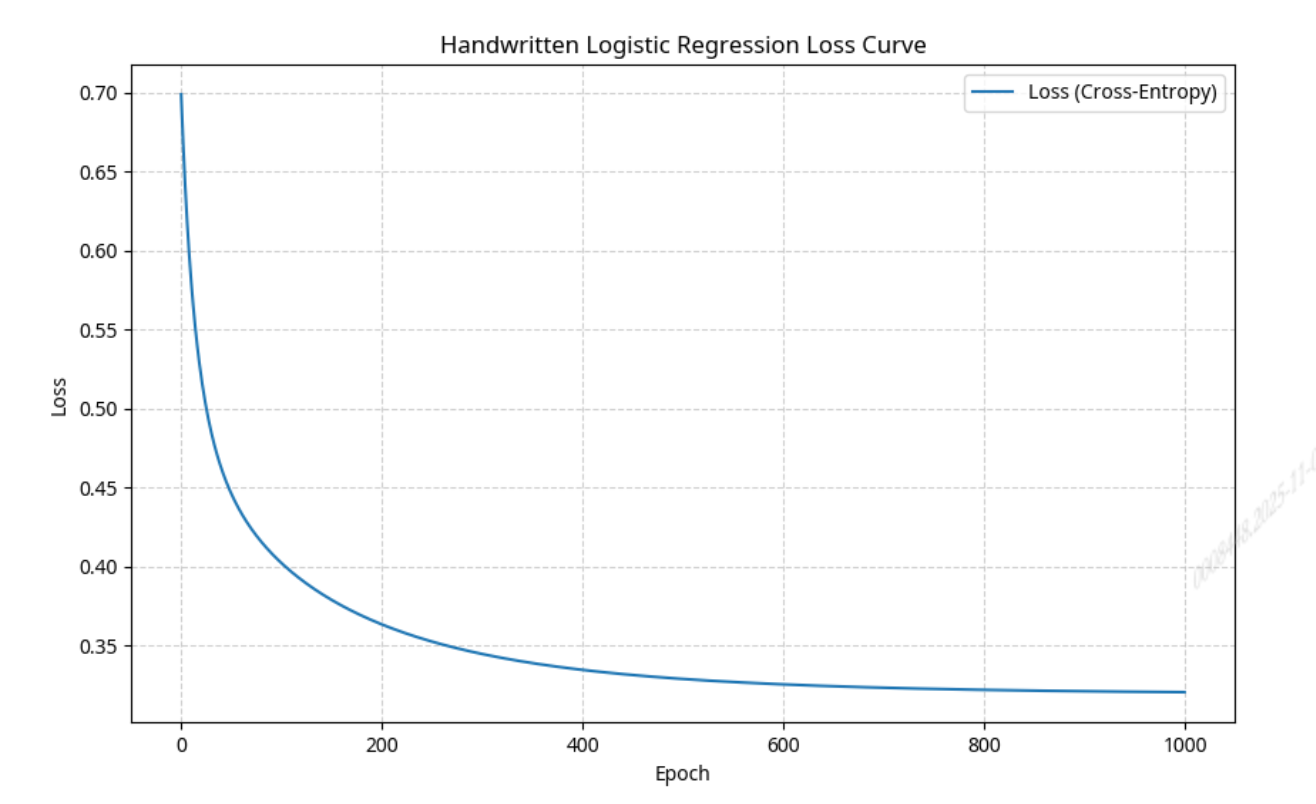
    plot_loss(lr_handwritten.loss_history, "Handwritten Logistic Regression Loss Curve")
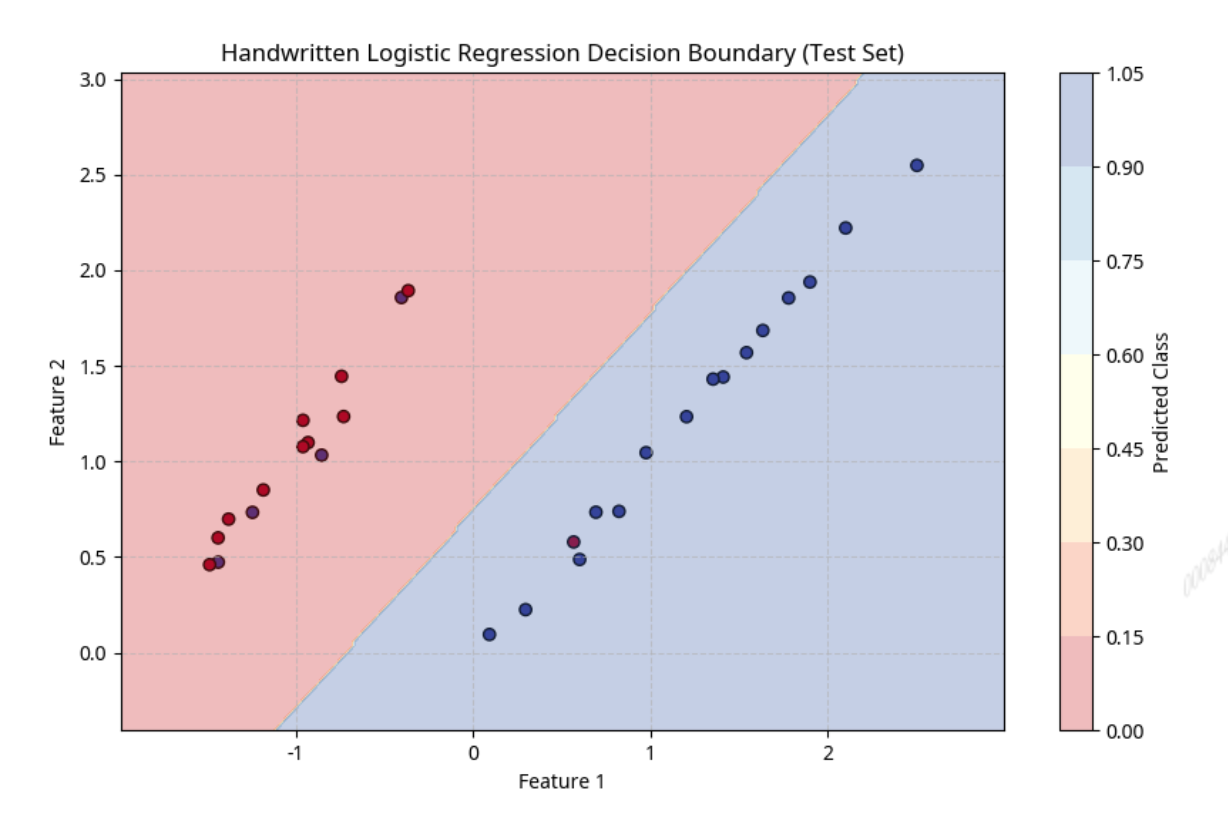
    plot_results(lr_handwritten, X_test, y_test, "Handwritten Logistic Regression Decision Boundary (Test Set)")
    
    print("手写模型损失曲线图已保存为: Handwritten_Logistic_Regression_Loss_Curve_loss_curve.png")
    print("手写模型决策边界图已保存为: Handwritten_Logistic_Regression_Decision_Boundary_(Test_Set)_decision_boundary.png")

5.2 sklearn实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# ----------------------------------------------------------------------
# 1. 数据生成
# ----------------------------------------------------------------------
def create_data():
    # 生成一个线性可分的数据集
    X, y = make_classification(
        n_samples=100, 
        n_features=2, 
        n_informative=2, 
        n_redundant=0, 
        n_classes=2, 
        n_clusters_per_class=1, 
        flip_y=0.1, 
        random_state=42
    )
    return X, y

# ----------------------------------------------------------------------
# 2. 可视化函数
# ----------------------------------------------------------------------
def plot_decision_boundary(model, X, y, title, filename):
    # 绘制数据点和决策边界
    plt.figure(figsize=(10, 6))
    
    # 绘制数据点
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.RdYlBu, marker='o', edgecolors='k')
    
    # 绘制决策边界
    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                         np.arange(y_min, y_max, 0.02))
    
    # 预测网格点的类别
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    # 绘制等高线图
    plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlBu)
    
    plt.title(title)
    plt.xlabel("Feature 1")
    plt.ylabel("Feature 2")
    plt.colorbar(label='Predicted Class')
    plt.grid(True, linestyle='--', alpha=0.6)
    
    # 保存决策边界图
    plt.savefig(filename)
    plt.close()

# ----------------------------------------------------------------------
# 3. 运行 Sklearn 模型
# ----------------------------------------------------------------------
if __name__ == "__main__":
    # 1. 准备数据
    X, y = create_data()
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
    
    # 2. 训练模型
    # solver='liblinear' 适用于小数据集，'lbfgs' 是默认且适用于大数据集
    # C=1.0 是正则化强度的倒数，这里使用默认值
    lr_sklearn = LogisticRegression(solver='liblinear', random_state=42)
    print("--- 开始训练 Sklearn 逻辑回归模型 ---")
    lr_sklearn.fit(X_train, y_train)
    print("--- 训练完成 ---")
    
    # 3. 评估模型
    y_pred_test = lr_sklearn.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred_test)
    print(f"测试集准确率: {accuracy * 100:.2f}%")
    
    # 4. 可视化结果
    filename = "Sklearn_Logistic_Regression_Decision_Boundary_Test_Set_decision_boundary.png"
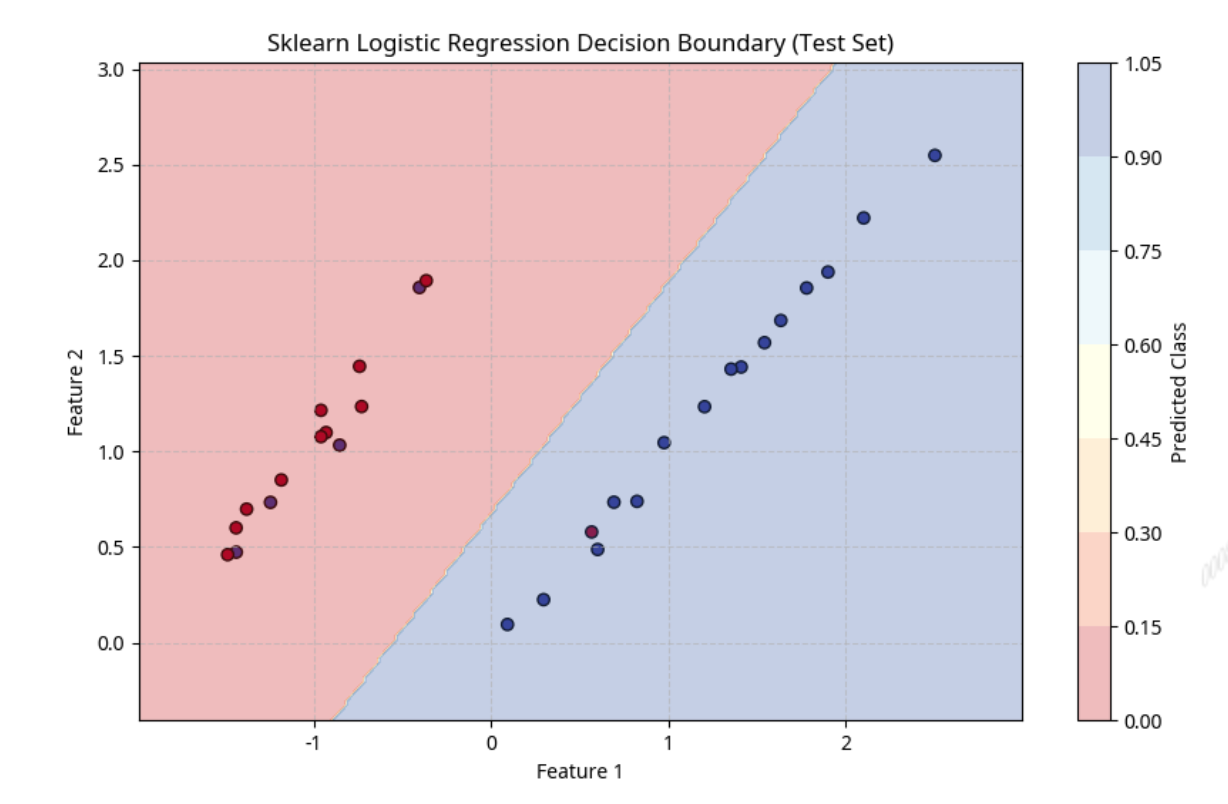
    plot_decision_boundary(lr_sklearn, X_test, y_test, "Sklearn Logistic Regression Decision Boundary (Test Set)", filename)
    
    print(f"Sklearn 模型决策边界图已保存为: {filename}")
    
    # 注意：Sklearn 的 LogisticRegression 默认不提供 Loss 历史记录，
    # 因此无法直接绘制 Loss 曲线，这是手写实现的一个优势。
    print("注意：Sklearn 默认不提供 Loss 历史记录，无法绘制 Loss 曲线。")

---

总结：通往神经网络的桥梁

逻辑回归是机器学习中最重要的模型之一，它完成了从回归到分类的转变，并引入了两个对深度学习至关重要的概念：

1. 激活函数（Sigmoid）：引入非线性，是神经网络中每一层的基础。
2. 交叉熵损失：分类问题最常用的损失函数，是神经网络训练的基石。

通过逻辑回归，我们已经掌握了构建一个单层非线性分类器的所有要素。下一章，我们将把这个“单层”结构推广到“多层”，正式开启神经网络的学习。