🌞欢迎来到matlab的世界 
🌈博客主页：卿云阁

💌欢迎关注🎉点赞👍收藏⭐️留言📝

🌟本文由卿云阁原创！

📆首发时间：🌹2025年9月27日🌹

✉️希望可以和大家一起完成进阶之路！

🙏作者水平很有限，如果发现错误，请留言轰炸哦！万分感谢！

---

目录

分类算法举例（BP）

回归算法举例（CNN）

时间预测算法举例（LSTM）

分类算法举例（BP）

数据集介绍：

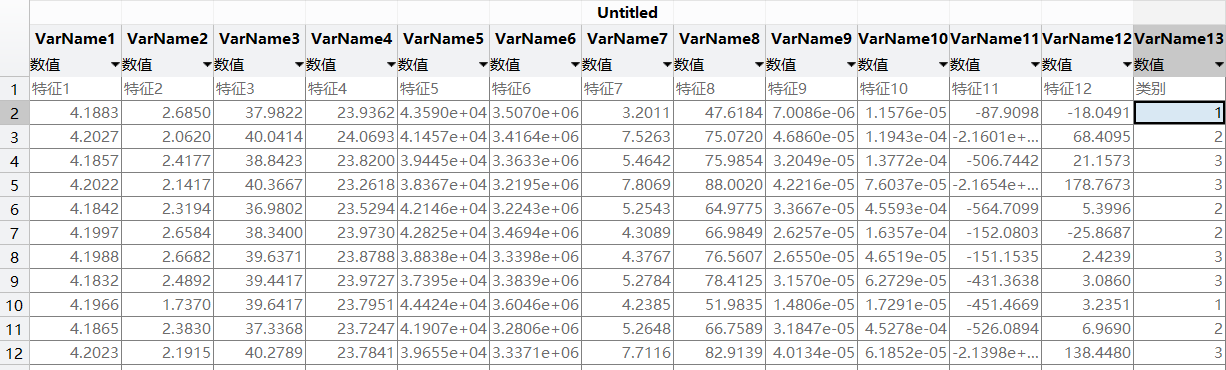
      特征列（VarName1 - VarName12）：从 “特征 1” 到 “特征 12”，共 12 个特征，每个特征列下

有对应的数值数据。这些数值可能是从实际场景中采集的不同属性值，用于描述样本的特征，例如

可能是某种产品的不同参数、实验的不同观测指标等。

      类别列（VarName13）：即 “类别” 列，用于表示每个样本所属的类别，目前看到的类别标签有 1、2、3 等，说明这是一个多分类问题（至少包含 3 个类别）。

%% 初始化
clear
close all
clc
warning off

%%  导入数据
res = xlsread('数据集.xlsx');
%%  分析数据
num_class = length(unique(res(:, end)));  % 类别数（Excel最后一列放类别）
num_res = size(res, 1);                   % 样本数（每一行，是一个样本）
num_size = 0.7;                           % 训练集占数据集的比例
res = res(randperm(num_res), :);          % 打乱数据集（不打乱数据时，注释该行）
flag_conusion = 1;                        % 标志位为1，打开混淆矩阵（要求2018版本及以上）

%%  设置变量存储数据
P_train = []; P_test = [];
T_train = []; T_test = [];

%%  划分数据集
for i = 1 : num_class
    mid_res = res((res(:, end) == i), :);           % 循环取出不同类别的样本
    mid_size = size(mid_res, 1);                    % 得到不同类别样本个数
    mid_tiran = round(num_size * mid_size);         % 得到该类别的训练样本个数

    P_train = [P_train; mid_res(1: mid_tiran, 1: end - 1)];       % 训练集输入
    T_train = [T_train; mid_res(1: mid_tiran, end)];              % 训练集输出

    P_test  = [P_test; mid_res(mid_tiran + 1: end, 1: end - 1)];  % 测试集输入
    T_test  = [T_test; mid_res(mid_tiran + 1: end, end)];         % 测试集输出
end

%%  数据转置
P_train = P_train'; P_test = P_test';
T_train = T_train'; T_test = T_test';

%%  得到训练集和测试样本个数
M = size(P_train, 2);
N = size(P_test , 2);
%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test  = mapminmax('apply', P_test, ps_input);
t_train = ind2vec(T_train);
t_test  = ind2vec(T_test );

%%  建立模型
net = newff(p_train, t_train, 6);

%%  设置训练参数
net.trainParam.epochs = 1000;   % 最大迭代次数
net.trainParam.goal = 1e-6;     % 目标训练误差
net.trainParam.lr = 0.01;       % 学习率

%%  训练网络
net = train(net, p_train, t_train);

%%  仿真测试
t_sim1 = sim(net, p_train);
t_sim2 = sim(net, p_test );

%%  数据反归一化
T_sim1 = vec2ind(t_sim1);
T_sim2 = vec2ind(t_sim2);

%%  数据排序
[T_train, index_1] = sort(T_train);
[T_test , index_2] = sort(T_test );

T_sim1 = T_sim1(index_1);
T_sim2 = T_sim2(index_2);

%%  性能评价
error1 = sum((T_sim1 == T_train)) / M * 100 ;
error2 = sum((T_sim2 == T_test )) / N * 100 ;

%%  绘图
figure
plot(1: M, T_train, 'r-*', 1: M, T_sim1, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {strcat('训练集预测结果对比：', ['准确率=' num2str(error1) '%'])};
title(string)
grid

figure
plot(1: N, T_test, 'r-*', 1: N, T_sim2, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {strcat('测试集预测结果对比：', ['准确率=' num2str(error2) '%'])};
title(string)
grid

%%  混淆矩阵
figure
cm = confusionchart(T_train, T_sim1);
cm.Title = 'Confusion Matrix for Train Data';
cm.ColumnSummary = 'column-normalized';
cm.RowSummary = 'row-normalized';
    
figure
cm = confusionchart(T_test, T_sim2);
cm.Title = 'Confusion Matrix for Test Data';
cm.ColumnSummary = 'column-normalized';
cm.RowSummary = 'row-normalized';

回归算法举例（CNN）

数据集介绍：

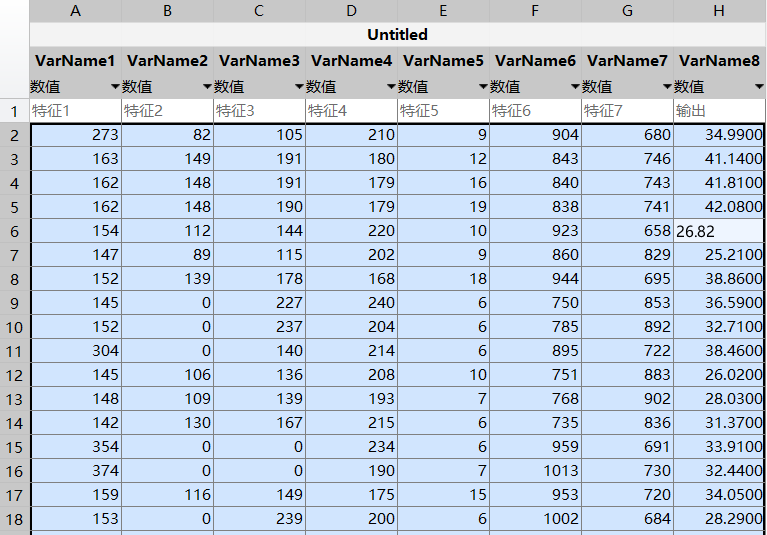
特征列（VarName1 - VarName7）：从 “特征 1” 到 “特征 7”，共 7 个特征，每个特征列下有对应

的数值数据。这些数值可能是从实际场景中采集的不同属性值，用于描述样本的特征，例如可能是

某种产品的不同参数、实验的不同观测指标等。
输出列（VarName8）：即 “输出” 列，用于表示每个样本对应的连续输出值，属于回归任务的目标

变量，可通过前面的 7 个特征来预测该输出值。

%% 初始化
clear
close all
clc
warning off

%%  导入数据
res = xlsread('数据集.xlsx');

%%  数据分析
num_size = 0.7;                              % 训练集占数据集比例
outdim = 1;                                  % 最后一列为输出
num_samples = size(res, 1);                  % 样本个数
res = res(randperm(num_samples), :);         % 打乱数据集（不希望打乱时，注释该行）
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征维度

%%  划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);

P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);

%%  数据归一化
[P_train, ps_input] = mapminmax(P_train, 0, 1);
P_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%%  数据平铺
%   将数据平铺成1维数据只是一种处理方式
%   也可以平铺成2维数据，以及3维数据，需要修改对应模型结构
%   但是应该始终和输入层数据结构保持一致
p_train =  double(reshape(P_train, f_, 1, 1, M));
p_test  =  double(reshape(P_test , f_, 1, 1, N));
t_train =  double(t_train)';
t_test  =  double(t_test )';

%%  构造网络结构
% ----------------------  修改模型结构时需对应修改fical.m中的模型结构  --------------------------

layers = [
 imageInputLayer([f_, 1, 1])                        % 输入层 输入数据规模[f_, 1, 1]
 
 convolution2dLayer([3, 1], 16, 'Padding', 'same')  % 卷积核大小 3*1 生成16张特征图
 batchNormalizationLayer                            % 批归一化层
 reluLayer                                          % Relu激活层
 
 convolution2dLayer([3, 1], 32, 'Padding', 'same')  % 卷积核大小 3*1 生成32张特征图
 batchNormalizationLayer                            % 批归一化层
 reluLayer                                          % Relu激活层

 dropoutLayer(0.2)                                  % Dropout层
 fullyConnectedLayer(outdim)                        % 全连接层
 regressionLayer];                                  % 回归层

%%  参数设置
options = trainingOptions('adam', ...      % Adam 梯度下降算法
    'MaxEpochs', 500, ...                  % 最大训练次数 500
    'InitialLearnRate', 1e-3, ...          % 初始学习率为 0.001
    'L2Regularization', 1e-4, ...          % L2正则化参数
    'LearnRateSchedule', 'piecewise', ...  % 学习率下降
    'LearnRateDropFactor', 0.1, ...        % 学习率下降因子 0.1
    'LearnRateDropPeriod', 400, ...        % 经过450次训练后 学习率为 0.001 * 0.1
    'Shuffle', 'every-epoch', ...          % 每次训练打乱数据集
    'ValidationPatience', Inf, ...         % 关闭验证
    'Plots', 'training-progress', ...      % 画出曲线
    'Verbose', false);
%%  训练模型
net = trainNetwork(p_train, t_train, layers, options);

%%  仿真验证
t_sim1 = predict(net, p_train);
t_sim2 = predict(net, p_test );

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);

%%  均方根误差
error1 = sqrt(sum((T_sim1' - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2' - T_test ).^2) ./ N);

%%  绘制网络分析图
analyzeNetwork(layers)

%%  绘图
figure
plot(1: M, T_train, 'r-*', 1: M, T_sim1, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['RMSE=' num2str(error1)]};
title(string)
xlim([1, M])
grid

figure
plot(1: N, T_test, 'r-*', 1: N, T_sim2, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比'; ['RMSE=' num2str(error2)]};
title(string)
xlim([1, N])
grid

%%  相关指标计算
%  R2
R1 = 1 - norm(T_train - T_sim1')^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test  - T_sim2')^2 / norm(T_test  - mean(T_test ))^2;

disp(['训练集数据的R2为：', num2str(R1)])
disp(['测试集数据的R2为：', num2str(R2)])

%  MAE
mae1 = sum(abs(T_sim1' - T_train)) ./ M ;
mae2 = sum(abs(T_sim2' - T_test )) ./ N ;

disp(['训练集数据的MAE为：', num2str(mae1)])
disp(['测试集数据的MAE为：', num2str(mae2)])

%  MBE
mbe1 = sum(T_sim1' - T_train) ./ M ;
mbe2 = sum(T_sim2' - T_test ) ./ N ;

disp(['训练集数据的MBE为：', num2str(mbe1)])
disp(['测试集数据的MBE为：', num2str(mbe2)])

%  MAPE
mape1 = sum(abs((T_sim1' - T_train)./T_train)) ./ M ;
mape2 = sum(abs((T_sim2' - T_test )./T_test )) ./ N ;

disp(['训练集数据的MAPE为：', num2str(mape1)])
disp(['测试集数据的MAPE为：', num2str(mape2)])
%  RMSE
disp(['训练集数据的RMSE为：', num2str(error1)])
disp(['测试集数据的RMSE为：', num2str(error2)])
%%  绘制散点图
sz = 25;
c = 'b';

figure
scatter(T_train, T_sim1, sz, c)
hold on
plot(xlim, ylim, '--k')
xlabel('训练集真实值');
ylabel('训练集预测值');
xlim([min(T_train) max(T_train)])
ylim([min(T_sim1) max(T_sim1)])
title('训练集预测值 vs. 训练集真实值')

figure
scatter(T_test, T_sim2, sz, c)
hold on
plot(xlim, ylim, '--k')
xlabel('测试集真实值');
ylabel('测试集预测值');
xlim([min(T_test) max(T_test)])
ylim([min(T_sim2) max(T_sim2)])
title('测试集预测值 vs. 测试集真实值')

时间预测算法举例（LSTM）

数据集介绍：

VarName1（文本列）：表示时间，格式为 “X 时 Y 分 00 秒”，呈现出按时间顺序递增的规律，比

如从 “0 时 15 分 00 秒” 依次到 “2 时 45 分 00 秒” 等，可能是对某个过程进行观测的时间节点记

录。VarName2（数值列）：对应每个时间点的数值数据，这些数值随着时间推移呈现出一定的

变、化趋势，可用于分析该时间序列下数据的变化规律，适合进行时间序列相关的分析，比如趋势

预测、周期性探究等。

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%%  导入数据（时间序列的单列数据）
result = xlsread('数据集.xlsx');

%%  数据分析
num_samples = length(result);  % 样本个数 
kim = 15;                      % 延时步长（kim个历史数据作为自变量）
zim =  1;                      % 跨zim个时间点进行预测

%%  划分数据集
for i = 1: num_samples - kim - zim + 1
    res(i, :) = [reshape(result(i: i + kim - 1), 1, kim), result(i + kim + zim - 1)];
end
%%  数据集分析
outdim = 1;                                  % 最后一列为输出
num_size = 0.7;                              % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征维度
% %%  划分训练集和测试集
% temp = 1: 1: 922;
% 
% P_train = res(temp(1: 700), 1: 15)';
% T_train = res(temp(1: 700), 16)';
% M = size(P_train, 2);
% 
% P_test = res(temp(701: end), 1: 15)';
% T_test = res(temp(701: end), 16)';
% N = size(P_test, 2);
%%  划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);

P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);

%%  数据归一化
[P_train, ps_input] = mapminmax(P_train, 0, 1);
P_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%%  数据平铺
% 将数据平铺成1维数据只是一种处理方式
% 也可以平铺成2维数据，以及3维数据，需要修改对应模型结构
% 但是应该始终和输入层数据结构保持一致
P_train =  double(reshape(P_train, f_, 1, 1, M));
P_test  =  double(reshape(P_test , f_, 1, 1, N));

t_train = t_train';
t_test  = t_test' ;

%%  数据格式转换
for i = 1 : M
    p_train{i, 1} = P_train(:, :, 1, i);
end

for i = 1 : N
    p_test{i, 1}  = P_test( :, :, 1, i);
end

%%  创建模型
layers = [
    sequenceInputLayer(f_)              % 建立输入层
    
    lstmLayer(10, 'OutputMode', 'last') % LSTM层
    reluLayer                           % Relu激活层
    
    fullyConnectedLayer(1)              % 全连接层
    regressionLayer];                   % 回归层

%%  参数设置
% options = trainingOptions('adam', ...       % Adam 梯度下降算法
%     'MaxEpochs', 1200, ...                  % 最大训练次数
%     'InitialLearnRate', 5e-3, ...           % 初始学习率
%     'LearnRateSchedule', 'piecewise', ...   % 学习率下降
%     'LearnRateDropFactor', 0.1, ...         % 学习率下降因子
%     'LearnRateDropPeriod', 800, ...         % 经过 800 次训练后 学习率为 0.005 * 0.1
%     'Shuffle', 'every-epoch', ...           % 每次训练打乱数据集
%     'Plots', 'training-progress', ...       % 画出曲线
%     'Verbose', false);
options = trainingOptions('adam', ...                 % 优化算法Adam
    'MaxEpochs', 300, ...                             % 最大训练次数
    'GradientThreshold', 1, ...                       % 梯度阈值
    'InitialLearnRate', 5e-3, ...                     % 初始学习率
    'LearnRateSchedule', 'piecewise', ...             % 学习率调整
    'LearnRateDropPeriod', 250, ...                   % 训练250次后开始调整学习率
    'LearnRateDropFactor',0.1, ...                    % 学习率调整因子
    'L2Regularization', 1e-4, ...                     % 正则化参数
    'ExecutionEnvironment', 'auto',...                % 训练环境
    'Verbose', false, ...                                 % 关闭优化过程
    'Plots', 'training-progress');                    % 画出曲线
%%  训练模型
net = trainNetwork(p_train, t_train, layers, options);

%%  仿真预测
t_sim1 = predict(net, p_train);
t_sim2 = predict(net, p_test );

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);

%%  均方根误差
error1 = sqrt(sum((T_sim1' - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2' - T_test ).^2) ./ N);

%%  查看网络结构
analyzeNetwork(net)

%%  绘图
figure
plot(1: M, T_train, 'r-', 1: M, T_sim1, 'b-', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['RMSE=' num2str(error1)]};
title(string)
xlim([1, M])
grid

figure
plot(1: N, T_test, 'r-', 1: N, T_sim2, 'b-', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比'; ['RMSE=' num2str(error2)]};
title(string)
xlim([1, N])
grid

%%  相关指标计算
% R2
R1 = 1 - norm(T_train - T_sim1')^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test  - T_sim2')^2 / norm(T_test  - mean(T_test ))^2;

disp(['训练集数据的R2为：', num2str(R1)])
disp(['测试集数据的R2为：', num2str(R2)])

% MAE
mae1 = sum(abs(T_sim1' - T_train)) ./ M ;
mae2 = sum(abs(T_sim2' - T_test )) ./ N ;

disp(['训练集数据的MAE为：', num2str(mae1)])
disp(['测试集数据的MAE为：', num2str(mae2)])

% MBE
mbe1 = sum(T_sim1' - T_train) ./ M ;
mbe2 = sum(T_sim2' - T_test ) ./ N ;

disp(['训练集数据的MBE为：', num2str(mbe1)])
disp(['测试集数据的MBE为：', num2str(mbe2)])

%  MAPE
mape1 = sum(abs((T_sim1' - T_train)./T_train)) ./ M ;
mape2 = sum(abs((T_sim2' - T_test )./T_test )) ./ N ;

disp(['训练集数据的MAPE为：', num2str(mape1)])
disp(['测试集数据的MAPE为：', num2str(mape2)])

%%  绘制散点图
sz = 25;
c = 'b';

figure
scatter(T_train, T_sim1, sz, c)
hold on
plot(xlim, ylim, '--k')
xlabel('训练集真实值');
ylabel('训练集预测值');
xlim([min(T_train) max(T_train)])
ylim([min(T_sim1) max(T_sim1)])
title('训练集预测值 vs. 训练集真实值')

figure
scatter(T_test, T_sim2, sz, c)
hold on
plot(xlim, ylim, '--k')
xlabel('测试集真实值');
ylabel('测试集预测值');
xlim([min(T_test) max(T_test)])
ylim([min(T_sim2) max(T_sim2)])
title('测试集预测值 vs. 测试集真实值')
%%%%%%%%%咸鱼号：默默科研仔