R语言绘图 | 列线图/诺莫图(Nomogram)和校准曲线(Calibration)| 代码注释 + 结果解读
好久不见!想我不啦!
前面已经介绍了高级森林图的画法,今天我们就来介绍另一种用于可视化Logistic或Cox回归分析结果的方式 —— 列线图(Alignment Diagram),也称诺莫图(Nomogram)。
我们先介绍一下列线图,大家如果不需要的话,也可以跳过这部分直接去看代码实现部分哟!
列线图是什么
列线图(Alignment Diagram),又称诺莫图(Nomogram图),是建立在多因素回归分析的基础上的,主要用于将多个预测指标整合到同一平面上,以可视化地表达预测模型中各个变量之间的相互关系。通过使用带有刻度的线段,并按照一定的比例在同一坐标系上绘制这些线段,以直观地展示不同预测指标对结果的影响程度。
**通常我们需要先进行回归分析,获得多因素回归模型的结果,然后再使用列线图(当然也可以用森林图)来呈现这些结果。**列线图将复杂的数学模型转化为直观、易于理解的图形,使预测模型的结果更具有可读性,帮助我们更容易理解和解释模型中各个变量之间的相互关系,以便更好地应用模型的预测结果对患者进行评估。
列线图还可以和**校准曲线(Calibration)、**ROC曲线等其他工具结合使用,以全面评估模型的性能和准确性。
单因素Cox + Lasso回归 + 多因素Cox回归 + 森林图/列线图,是毕竟经典的分析方法,有兴趣的小伙伴可以查看我们之前分享的相关内容进行学习。
看完还不会来揍/找我 | 基于 LASSO 回归筛选变量以构建预测模型 | 附完整代码 + 注释
看完还不会来揍/找我 | 构建 Cox 比例风险回归模型 | 绘制森林图 (forestplot) | 附完整代码 + 注释
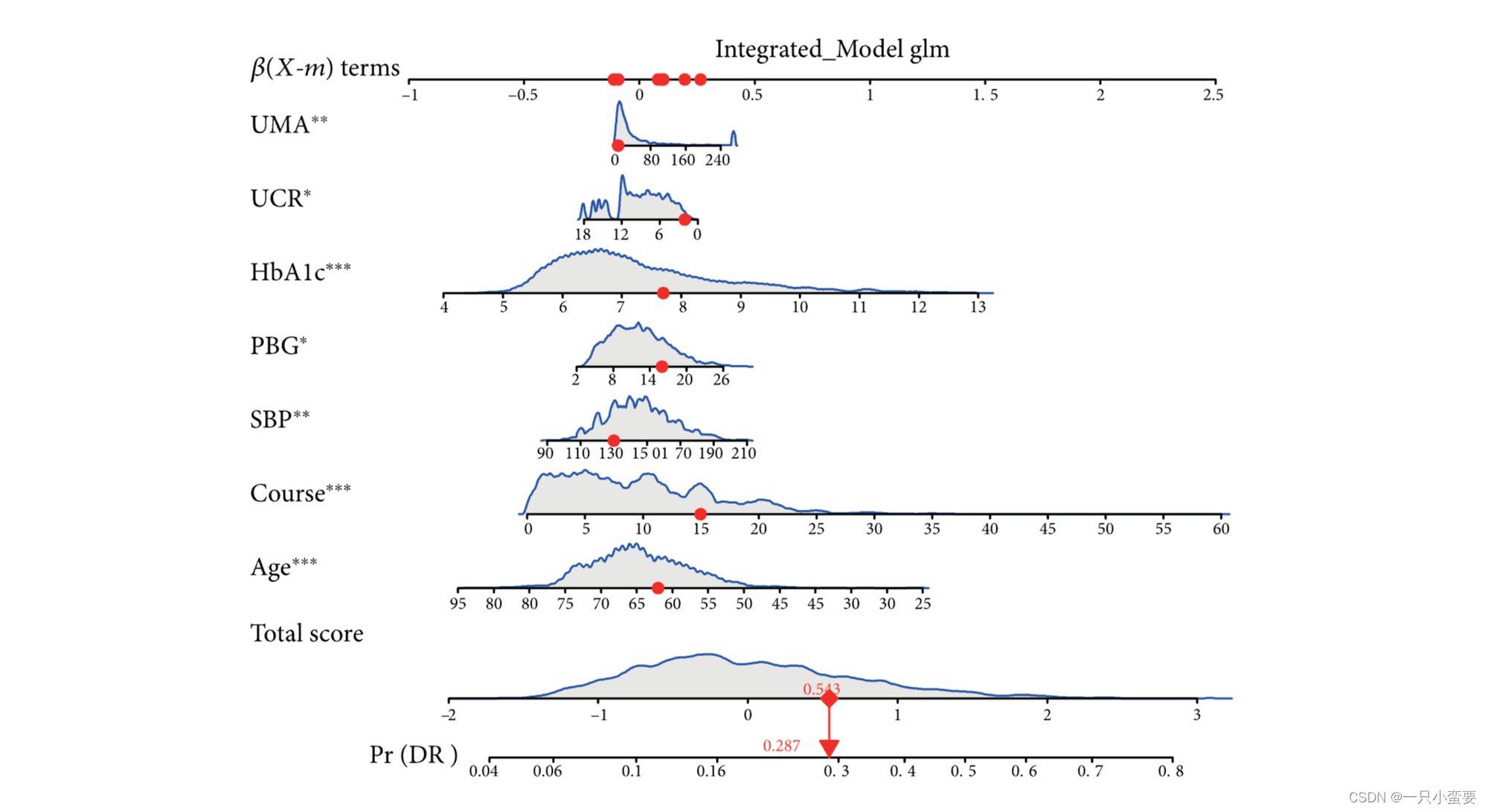
下图就是一张普普通通平平无奇的列线图!

图片来源:Mo R, Shi R, Hu Y, Hu F. Nomogram-Based Prediction of the Risk of Diabetic Retinopathy: A Retrospective Study. J Diabetes Res. 2020 Jun 7;2020:7261047.
让我们把它掰开了揉碎了介绍一下!
列线图的核心原理
- 多因素回归模型:首先,通过多因素回归分析(例如Cox回归、Logistic回归等),建立了一个预测模型,该模型描述了多个自变量(影响因素)与一个因变量(通常是某种事件的发生概率或时间)之间的关系。模型中的回归系数表示每个自变量对因变量的影响程度。
- 赋分:根据模型中各个自变量的回归系数大小,为每个自变量的不同取值水平赋予一定的分数。这些分数通常是根据经验或统计方法确定的,反映了每个自变量对结果的相对重要性。
- 总评分:将每个自变量的分数相加,得到一个总评分。这个总评分反映了特定个体的预测结果。
- 预测结果:通过将总评分与结局事件(例如疾病发生、生存率等)的发生概率之间的函数转换关系,计算出个体的预测结果。这可以帮助我们估计患者的风险或预测特定事件的概率。
- 可视化呈现:最后,将赋分和总评分以带有刻度的线段的形式按照一定比例绘制在同一平面上,形成列线图。列线图直观地展示了模型中各个自变量之间的相互关系,以及总评分与预测结果之间的关联。
列线图解读

这个图图是我们今天的数据生成的,会在后面有具体介绍!
我们可以看到列线图主要由左边的名称以及右边对应的带有刻度的线段所组成。
列线图的名称主要包括三类:
- 预测模型中的变量名称:例如图中的年龄(Age)、分期(Stage)等信息,每一个变量对应的线段上都标注了刻度,代表了该变量的可取值范围,而线段的长度则反映了该因素对结局事件的贡献大小。
- 得分,包括单项得分,即图中的Point,表示每个变量在不同取值下所对应的单项分数,以及总得分,即Total Point,表示所有变量取值后对应的单项分数加起来合计的总得分。
- 预测概率:例如图中的Pr(Time < 730)(这个可以有不同的命名方式,我们可以自己设定),表示2年的生存概率。
咱们举个例子,假设有一名女性患者,年龄为45岁,家族中有乳腺癌病史,她正在接受荷尔蒙替代疗法。医生在和患者交代病情的时候,为了更清晰地向患者解释疾病的严重程度,就甩出一张列线图,告诉这位患者,以她目前的疾病状态,预测未来3年、5年的生存概率分别是68%、42%。
医生是怎么算出来的呢?其实也很简单啦!比如这位患者年龄为45岁,我们就在列线图年龄为45岁的地方向上画一条垂直线,即可得到其对应的得分(Points)约为40分。患者性别为女性,对应的分数为1分,以此类推,找出每个变量状态下对应的得分。最后将所有变量的得分相加,得到患者的总得分(Total Points)约为234分,然后在总得分的位置向下画一条垂直线,就可以知道该患者对应的未来3年、5年的生存率啦,不知道我这么介绍大家好不好理解嘞!
如果有小伙伴不理解没关系!我们继续往后看,后面我们会在实例中为大家进行详细解读!
接下来,我们进入大家最最最喜爱的部分!代码实战 + 结果解读!
代码实战
今日份实战的数据我已经上传到了GitHub,大家可以在公众号后台回复列线图,即可获得存放数据的链接。不过我在分享过程中也会把每一步的输入数据和输出结果进行展示,大家可以作为参考并调整自己的数据格式,然后直接用自己的数据跑,也是没有任何问题的!
我们今天主要以Cox回归为例进行介绍,逻辑回归与Cox回归绘图方式一致,大家后面可以自己尝试一下哟!
Cox回归在survival和rms这两个包中都可以实现,咱们两个函数都尝试一下,比较一下两个函数之间的区别。
survival包中的coxph函数
############################## 列线图(Nomogram)###############################
# cox回归在 survival 和 rms 这两个包中都可以实现,咱们两个函数都尝试一下,比较一下两个函数之间的区别。
# 加载这两个包先
library(survival)
library(rms)
# 加载用于cox回归的临床数据
tcga_gbmlgg_cli <- readRDS("~/YaoKnow/R_Plot/nomogram/data/tcga_gbmlgg_cli.rds")
head(tcga_gbmlgg_cli)
# # A tibble: 6 × 9
# Sample Time Status Gender Age IDH_status MGMT_promoter_status Stage Group
# <chr> <dbl> <dbl> <chr> <dbl> <chr> <chr> <chr> <chr>
# 1 TCGA-02-0047-01 448 1 Male 79 Wildtype Un-methylated WHO IV GBM
# 2 TCGA-02-0055-01 76 1 Female 62 Wildtype Un-methylated WHO IV GBM
# 3 TCGA-02-2483-01 691 1 Male 44 Mutant Methylated WHO IV GBM
# 4 TCGA-02-2485-01 1561 1 Male 53 Wildtype Un-methylated WHO IV GBM
# 5 TCGA-02-2486-01 618 1 Male 64 Wildtype Un-methylated WHO IV GBM
# 6 TCGA-06-0125-01 1448 1 Female 64 Wildtype Methylated WHO IV GBM
# 我们把变量改为适用于计分展示的观测值,方便后面图图里的示例计分展示!也可以不这么干!大家可以都尝试一下!
tcga_gbmlgg_cli$IDH_status <- ifelse(tcga_gbmlgg_cli$IDH_status == "Mutant", 1, 0)
tcga_gbmlgg_cli$MGMT_promoter_status <- ifelse(tcga_gbmlgg_cli$MGMT_promoter_status == "Methylated", 1, 0)
tcga_gbmlgg_cli$Stage <- ifelse(tcga_gbmlgg_cli$Stage == "WHO IV", 4,
ifelse(tcga_gbmlgg_cli$Stage == "WHO III", 3, 2))
# 我们先来用 survival 包的 coxph 函数构造 cox 回归模型
library(survival)
# 注意:大家需要选择之前做cox回归模型时显著的那几个变量,然后进行cox回归
mul_cox <- coxph(Surv(Time, Status) ~ Age + IDH_status + MGMT_promoter_status + Stage, data = tcga_gbmlgg_cli)
mul_cox
# Call:
# coxph(formula = Surv(Time, Status) ~ Age + IDH_status + MGMT_promoter_status +
# Stage, data = tcga_gbmlgg_cli)
#
# coef exp(coef) se(coef) z p
# Age 0.035940 1.036594 0.006031 5.959 2.54e-09
# IDH_status -1.096061 0.334185 0.230975 -4.745 2.08e-06
# MGMT_promoter_status -0.284991 0.752021 0.167778 -1.699 0.0894
# Stage 0.696942 2.007604 0.134074 5.198 2.01e-07
#
# Likelihood ratio test=322.9 on 4 df, p=< 2.2e-16
# n= 626, number of events= 214
# (48 observations deleted due to missingness)
咱们解读一下Cox回归的结果:
-
模型公式:
- 拟合的 Cox 回归模型的公式:
Surv(Time, Status) ~ Age + IDH_status + MGMT_promoter_status + Stage Surv(Time, Status)表示生存时间(Time)和生存状态(Status)是模型的因变量。- 模型考虑了四个自变量:年龄(Age)、IDH状态(IDH_status)、MGMT启动子状态(MGMT_promoter_status)和疾病分期(Stage)。
- 拟合的 Cox 回归模型的公式:
-
模型系数:
对于每个预测变量,包括年龄(Age)、IDH状态(IDH_status)、MGMT甲基化状态(MGMT_promoter_status)和分期(Stage),给出了它们的模型系数(coef)、模型系数的指数形式(exp(coef)),以及模型系数的标准误差(se(coef))。
模型系数指数形式的解释:给出了模型系数的指数形式(exp(coef)),表示风险比(Hazard Ratio,HR)。HR用于衡量不同预测变量对生存时间的影响。指数形式大于1表示增加风险,小于1表示降低风险。
- 年龄(Age)的系数为 0.035940,表示每增加一单位年龄,风险比(hazard ratio)约为 1.0366,即生存风险略微增加。
- IDH状态(IDH_status)的系数为 -1.096061,表示IDH状态为Mutant相对于Wildtype的风险比为 0.3342,即生存风险较低。
- MGMT启动子状态(MGMT_promoter_status)的系数为 -0.284991,但在统计学上不够显著(p-value=0.0894),这表示该变量对生存风险的影响可能不太明显。
- 疾病分期(Stage)的系数为 0.696942,表示每增加一个单位的疾病分期,风险比约为 2.0076,即生存风险显著增加。
-
z值和p值:
z值用于检验模型系数是否显著,p值则表示检验的显著性水平。在这里,z值较大,p值非常小,表明这些系数在统计上是显著的。
-
Likelihood Ratio Test:
- 似然比检验统计量为 322.9,自由度为 4,p 值非常接近于零(p < 2.2e-16),表明模型是显著的,模型中的至少一个变量对生存时间有显著影响。
-
样本和事件数量:
- 总样本量(n)为 626,表示在分析中使用了 626 个观测数据点。
- 事件数量(number of events)为 214,表示在这些数据中发生了 214 个事件(例如死亡事件)。
- 有 48 个观测数据因缺失而被删除,这些数据点没有参与模型的拟合和分析。
这个 Cox 回归模型分析了生存数据,发现年龄、IDH状态、疾病分期这些因素与生存时间之间存在显著关联,而MGMT启动子状态在统计学上影响不太明显。模型拟合良好,可以用于预测个体的生存风险。
rms包中的cph函数
# 我们再用 rms 包的 cph 函数构造 cox 回归模型
library(rms)
# 选择和上面相同的变量,进行cox回归
mul_cox_2 <- cph(Surv(Time, Status) ~ Age + IDH_status + MGMT_promoter_status + Stage, data = tcga_gbmlgg_cli, x = TRUE, y = TRUE, surv = TRUE)
# x = TRUE, y = TRUE, surv = TRUE:这些参数用于控制cph函数的输出内容。
# x = TRUE表示要输出模型的系数(回归系数),
# y = TRUE表示要输出模型的Survival(生存)函数估计结果,
# surv = TRUE表示要输出生存曲线估计的结果。
mul_cox_2
# Frequencies of Missing Values Due to Each Variable
# Surv(Time, Status) Age IDH_status MGMT_promoter_status Stage
# 3 2 9 34 1
#
# Cox Proportional Hazards Model
#
# cph(formula = Surv(Time, Status) ~ Age + IDH_status + MGMT_promoter_status +
# Stage, data = tcga_gbmlgg_cli, x = TRUE, y = TRUE, surv = TRUE)
#
#
# Model Tests Discrimination
# Indexes
# Obs 626 LR chi2 322.85 R2 0.413
# Events 214 d.f. 4 R2(4,626)0.399
# Center 2.6774 Pr(> chi2) 0.0000 R2(4,214)0.775
# Score chi2 405.94 Dxy 0.718
# Pr(> chi2) 0.0000
#
# Coef S.E. Wald Z Pr(>|Z|)
# Age 0.0359 0.0060 5.96 <0.0001
# IDH_status -1.0961 0.2310 -4.75 <0.0001
# MGMT_promoter_status -0.2850 0.1678 -1.70 0.0894
# Stage 0.6969 0.1341 5.20 <0.0001
咱们解读一下这个Cox回归的结果:
-
缺失值情况:
Surv(Time, Status)中有 3 个缺失值。Age中有 2 个缺失值。IDH_status中有 9 个缺失值。MGMT_promoter_status中有 34 个缺失值。Stage中有 1 个缺失值。
-
Cox Proportional Hazards Model:
使用 Cox 比例风险模型,该模型基于生存数据拟合,包括了年龄(Age)、IDH状态(IDH_status)、MGMT启动子状态(MGMT_promoter_status)和疾病分期(Stage)这些协变量。
接下来,展示了模型的一些测试结果和判别指数。这些指标用于评估模型的质量和拟合程度:
- 观测数(Obs):数据中的总观测数。
- 事件数(Events):发生了生存事件的观测数。
- LR chi2:Likelihood Ratio Chi-Square,用于测试模型是否显著。
- d.f.:自由度,指的是模型中估计的参数数量。
- Pr(> chi2):P值,用于判断模型是否显著。
- Score chi2:Score Test的Chi-Square统计量。
- Discrimination Indexes:判别指数,包括C统计量(Concordance Index)和Dxy指数,用于评估模型的区分度。
- R2:模型的解释力,表示模型解释了总方差的百分比。
-
模型系数:
在“Coef”列中列出了每个自变量的回归系数,以及标准误差(S.E.)和Wald Z统计量。每个自变量的回归系数表示其对生存时间的影响程度:
- 年龄(Age)的系数为 0.0359,表示每增加一单位年龄,风险比(hazard ratio)约为 1.0366,即生存风险略微增加。
- IDH状态(IDH_status)的系数为 -1.0961,表示IDH状态为Mutant相对于Wildtype的风险比为 0.3342,即生存风险较低。
- MGMT启动子状态(MGMT_promoter_status)的系数为 -0.2850,但在统计学上不够显著(p-value=0.0894),这表示该变量对生存风险的影响可能不太明显。
- 疾病分期(Stage)的系数为 0.6969,表示每增加一个单位的疾病分期,风险比约为 2.0076,即生存风险显著增加。
这个 Cox 回归模型分析了生存数据,发现年龄、IDH状态、疾病分期这些因素与生存时间之间存在显著关联,而MGMT启动子状态在统计学上影响不太明显。模型拟合良好,可以用于预测个体的生存风险。同时,需要注意的是,模型中的部分变量存在缺失值,这可能需要额外的处理或分析。
接下来,我们就开始正式画图图啦!
rms包中的nomogram函数
rms包中的nomogram函数的输入数据需要是rms包构建的回归模型,当然这个包的模型构建函数还是蛮齐全的,基本可以满足我们的需求。
# 开始画图图!
# rms包中的nomogram函数
library(rms)
# 这里我们依据rms包中的cph函数获得的回归模型绘制列线图,选择1年、2年、3年的风险估计。
# 创建一个与生存分析相关的 Survival 对象
sur <- Survival(mul_cox_2)
# 定义用于不同时间点的生存函数
sur1 <- function(x) sur(365, x) # 1年生存
sur2 <- function(x) sur(730, x) # 2年生存
sur3 <- function(x) sur(1095, x) # 3年生存
# 绘制 nomogram,可视化cox比例风险模型的结果
nom <- nomogram(mul_cox_2,
fun = list(sur1, sur2, sur3), # 为每个时间点指定生存函数
fun.at = c(0.05, seq(0.1, 0.9, by = 0.05), 0.95), # 设置诺莫图上的生存概率点
funlabel = c("1 year survival", "2 years survival", "3 years survival")) # 设置生存时间标签
plot(nom)

后面会对列线图进行详细解读!
regplot包中的regplot函数
regplot包中的regplot函数可以接受多种函数建立的模型作为输入,包括cph和coxph等。
# regplot包中的regplot函数
library(regplot)
# 可以接受多种函数建立的模型作为输入,包括cph和coxph等等,我们这里用coxph
# 使用regplot函数,绘制列线图,可视化cox比例风险模型的结果
regplot(mul_cox,
observation = tcga_gbmlgg_cli[6, ], # 指定进行计分展示的观测数据,这里使用了数据集中的第6行,当然也可以不展示
points = TRUE, # 在列线图上显示点
plots = c("density", "no plot"), # 设置要显示的图表类型,这里包括密度图和无图表
failtime = c(365, 730, 1095), # 指定预测的时间点,这里预测了1年、2年和3年的死亡风险,单位是day
odds = F, # 是否显示死亡几率
leftlabel = T, # 是否显示左侧标签
prfail = TRUE, # 在 Cox 回归中需要设置为 TRUE
showP = T, # 是否展示统计学差异
droplines = T, # 示例计分是否画线
# colors = "red", # 可以使用自定义的颜色
rank = "range", # 根据统计学差异的显著性进行变量的排序
interval = "confidence", # 使用置信区间进行可视化
title = "Cox regression") # 设置图表的标题
# Regression mul_cox coxph formula:
# Surv(Time, Status) `~` Age + IDH_status + MGMT_promoter_status + Stage
# CI: 0.391(0.285,0.482)
# CI: 0.805(0.688,0.879)
# CI: 0.944(0.863,0.977)
# [[1]]
# Stage Points
# 1 2.0 23
# 2 2.4 33
# 3 2.8 43
# 4 3.2 54
# 5 3.6 64
# 6 4.0 74
#
# [[2]]
# MGMT_promoter_status Points
# 1 0.0 51
# 2 0.8 43
#
# [[3]]
# IDH_status Points
# 1 0.0 71
# 2 0.2 63
# 3 0.4 54
# 4 0.6 46
# 5 0.8 38
# 6 1.0 30
#
# [[4]]
# Age Points
# 1 10 -5
# 2 20 8
# 3 30 21
# 4 40 35
# 5 50 48
# 6 60 61
# 7 70 75
# 8 80 88
# 9 90 101
#
# [[5]]
# Total Points Pr( Time < 365 )
# 1 50 0.0021
# 2 100 0.0081
# 3 150 0.0308
# 4 200 0.1134
# 5 250 0.3708
# 6 300 0.8319
# 7 350 0.9990
解读一下这个结果:
-
模型公式:
- 拟合的 Cox 回归模型的公式:
Surv(Time, Status) ~ Age + IDH_status + MGMT_promoter_status + Stage Surv(Time, Status)表示生存时间(Time)和生存状态(Status)是模型的因变量。- 模型包括了四个自变量:年龄(Age)、IDH状态(IDH_status)、MGMT启动子状态(MGMT_promoter_status)和疾病分期(Stage)。
- 拟合的 Cox 回归模型的公式:
-
风险比和置信区间:
对于每个自变量,给出了相应的风险比和置信区间(Confidence Interval,CI):
- 年龄(Age)的风险比为 0.391,CI 为 (0.285, 0.482)。这表示每增加一单位年龄,生存风险降低,且 CI 不包括 1,说明这是一个显著的影响。
- IDH状态(IDH_status)的风险比为 0.805,CI 为 (0.688, 0.879)。这表示相对于IDH状态为Wildtype,IDH状态为Mutant的生存风险较高。
- MGMT启动子状态(MGMT_promoter_status)的风险比为 0.944,CI 为 (0.863, 0.977)。这表示相对于MGMT启动子状态为Methylated,Un-methylated的生存风险较高。
- 疾病分期(Stage)的风险比和 CI 未提供。
-
各自变量的得分(Points):
对于每个自变量,给出了不同取值水平对应的得分(Points)。这些得分可用于计算个体的总得分。
比如年龄(Age)得分分布如下:
- 年龄 10 对应得分 -5
- 年龄 20 对应得分 8
- 年龄 30 对应得分 21
- 年龄 40 对应得分 35
- 年龄 50 对应得分 48
- 年龄 60 对应得分 61
- 年龄 70 对应得分 75
- 年龄 80 对应得分 88
- 年龄 90 对应得分 101
-
总得分(Total Points):
根据各自变量的得分,计算了每个个体的总得分(Total Points)。
-
生存概率(Pr( Time < 365 )):
显示了在不同总得分情况下,生存时间小于 365 天的概率。

图中的红色圆点和红色线段部分是我们通过observation = tcga_gbmlgg_cli[6, ]指定进行计分展示的观测数据,也就是数据集中的第6行的样本,我们预测其生存风险。我们可以看下这个患者的信息:
# 查看观测数据样本信息
tcga_gbmlgg_cli[6, ]
# # A tibble: 1 × 9
# Sample Time Status Gender Age IDH_status MGMT_promoter_status Stage Group
# <chr> <dbl> <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <chr>
# 1 TCGA-06-0125-01 1448 1 Female 64 0 1 4 GBM
模型涉及到四个变量,分别为年龄(Age)、IDH状态(IDH_status)、MGMT启动子状态(MGMT_promoter_status)和疾病分期(Stage)。我们可以将样本信息与列线图对应查看,可以发现样本信息被清晰地展现在了列线图中,年龄为64,通过红色线段与红色圆点标注,可以知道这个样本Age这个变量对应的Point为65(应该或许大概是,大差不差!具体数值会在模型中计算)。以此类推,我们可以在图中找到样本的每个变量对应的Point值,然后将所有值相加,即可得到Total Point。比如这个样本,我们可以在图中看到Total Point为253,而253对应的1年、2年、3年生存率分别约为0.391、0.805、0.944。这也进一步说明了列线图的内容,其实本质就是对模型各个参数的直观展示!
校准曲线
**校准曲线(Calibration Curve)**是用于评价分类模型(如Logistic回归模型)或生存分析模型(如Cox回归模型)性能的重要工具之一。它帮助我们了解模型的预测概率与实际观测之间的关系,以及模型是否正确估计了事件的概率。
校准曲线通常是一个散点图,其中横轴表示模型的预测概率或分数,纵轴表示实际观测的事件发生率(或者生存率,如果是生存分析模型)。在一个完美校准的模型中,散点应该位于一条45度对角线上,这意味着模型的预测与实际观测完全吻合。
然而,在实际情况下,模型通常存在一定程度的校准误差。校准曲线可以帮助我们识别这些误差。如果校准曲线上的点偏离45度对角线,就意味着模型在某些预测概率范围内表现不佳。例如,如果曲线上的点都位于对角线上方,那么模型可能高估了事件的概率;如果点都位于对角线下方,那么模型可能低估了事件的概率。
Hosmer-Lemeshow拟合优度检验也可以用于评估模型的校准性。这个检验通过将数据分成若干组,并比较每组内观测事件的平均预测概率和实际事件发生率来评估模型的拟合质量。如果检验结果显示模型与实际观测不一致,那么校准曲线上的偏差也可能会反映这一不一致性。
接下来我们绘制校准曲线试试吧!
# 校准曲线(Calibration Curve
# time.inc参数用于指定风险比计算的时间单位
mul_cox_2 <- cph(Surv(Time, Status) ~ Age + IDH_status + MGMT_promoter_status + Stage, data = tcga_gbmlgg_cli, x = TRUE, y = TRUE, surv = TRUE, time.inc = 365)
# 使用calibrate函数创建一个校准对象cal1
cal1 <- calibrate(mul_cox_2,
cmethod = 'KM', # 表示使用Kaplan-Meier(KM)估计方法进行校准
method = "boot", # 表示使用自助法(Bootstrap)进行校准,Bootstrap 是一种统计方法,它通过从原始数据中有放回地进行重采样来估计参数的不确定性和分布。在这里,Bootstrap 用于生成多个随机样本来估计校准曲线的分布,以便获得更可靠的校准结果。
u = 365, # 设置时间间隔,需要与之前模型中定义的time.inc一致
m = 66, # 每次抽样的样本量,根据样本量来确定,标准曲线一般将所有样本分为3组(在图中显示3个点)
B = 1000) # 抽样次数
# 绘制校准曲线
par(mar = c(6, 6, 3, 3))
plot(cal1, # 绘制校准曲线的数据
lwd=1, # 线条宽度为1
lty=1, # 线条类型为1(实线)
conf.int=T, # 是否显示置信区间
errbar.col="blue3", # 直线和曲线的误差线颜色设置为蓝色
col="red3", # 校准曲线的颜色设置为红色
xlim=c(0,1), # x轴的限制范围,从0到1
ylim=c(0,1), # y轴的限制范围,从0到1
xlab="Nomogram-Predicted Probability of 1-Year DFS", # x轴标签
ylab="Actual 1-Year DFS (proportion)", # y轴标签
subtitles = F) # 不显示副标题

我们还可以进一步修饰。
# 在校准曲线上添加一条直线
lines(cal1[,c('mean.predicted',"KM")],
type = 'b', # 连线的类型,可以是"p","b","o"
lwd = 2, # 连线的粗细
pch = 16, # 点的形状,可以是0-20
col = c("red3")) # 连线的颜色
# 移除默认的标题
mtext("")
# 绘制图形边框
box(lwd = 1) # 边框粗细
# 添加一条虚线表示对角线
abline(0,1, lty = 3, # 对角线为虚线
lwd = 2, # 对角线的粗细
col = c("black")) # 对角线的颜色

解读一下:
- x轴:x轴表示模型的预测概率或分数,通常在0到1的范围内。这是模型对事件发生的概率的估计。
- y轴:y轴表示实际观测的事件发生率(或生存率),也是在0到1的范围内。这是真实数据中事件发生的比例。
- 校准曲线:红色的曲线代表模型的校准曲线。校准曲线显示了模型的预测概率与实际观测之间的关系。理想情况下,校准曲线应该接近45度对角线,这表示模型的预测与实际观测完全吻合。
- 虚线:虚线代表理论的完美校准线,即45度对角线。如果校准曲线与这条线重合,说明模型的预测完全准确。
- 误差线:图中显示了校准曲线上的误差线(蓝色),用于表示校准曲线的不确定性。这些误差线通常是置信区间的表示,它们告诉我们校准曲线的估计可能存在的变化范围。
校准曲线的主要目的是评估模型的校准性。如果校准曲线与45度对角线接近一致,那么模型的预测概率与实际观测相符,模型是校准的。如果校准曲线偏离45度对角线,那么模型的预测可能存在系统性的偏差,或许需要进一步改进。同时,误差线可以帮助我们了解校准曲线估计的不确定性范围。
我们下期再见哟!
如果我的分享对你有用的话,欢迎关注点赞在看转发分享阿巴阿巴阿巴阿巴巴巴!这可是我的第一原动力!
蟹蟹你们的喜欢和支持!!!
啊对!如果小伙伴们有需求的话,也可以加入我们的交流群:一定要知道 | 我们的生信交流群终于来啦!
参考资料
- https://zhuanlan.zhihu.com/p/484924017
- https://zhuanlan.zhihu.com/p/481644625
- https://mp.weixin.qq.com/s/Uk0cC3xmWT8V7a1cSBV3ag
更多推荐
 已为社区贡献9条内容
已为社区贡献9条内容






















所有评论(0)