支持向量机SVM——线性分类

支持向量机（SVM）：二分类算法模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。用于解决模式识别领域中的数据分类问题，属于有监督学习算法。优点：当数据集较小时，分类效果优于神经网络。能造出最大间距的决策边界从而提高分类算法的鲁棒性。

1129S

866人浏览 · 2023-12-17 16:49:33

1129S · 2023-12-17 16:49:33 发布

最大化间隔：margin最大的数即为最大化的间隔

一、SVM相关概念

1、什么是支持向量机

支持向量机（SVM）：二分类算法模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。用于解决模式识别领域中的数据分类问题，属于有监督学习算法。

优点：当数据集较小时，分类效果优于神经网络。

能造出最大间距的决策边界从而提高分类算法的鲁棒性。

2、最大间隔与分类

在样本空间 $D=\left \{ x_{i},y_{i} \right \}_{i=1}^{m}$ $x\epsilon R^{n},y\epsilon \left \{ -1 ,1\right \}$ 中寻找一个超平面 $w^{T}x_{i}+b=0$ 用于区分不同样本

支持向量——距离超平面最近的点

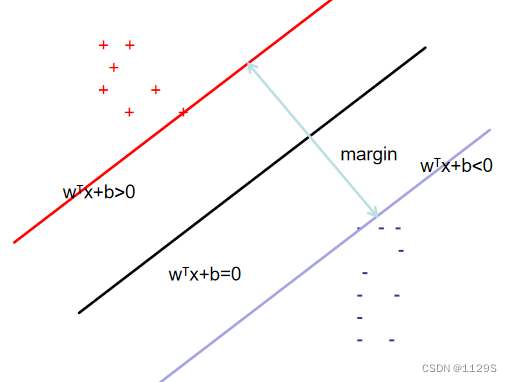
二分类有两个支持向量平面，这两个平面是平行的。超平面是位于这两个平面中间的。

在多种超平面中应选择哪种？

红线标注直线（最中间）为最优选择——容忍度好，鲁棒性高，泛化能力强，可最大化决策边界边缘

间隔margin $margin=\frac{|f(x)|}{||w||}$

最大化间隔：margin最大的数即为最大化的间隔

定义我们待求的超平面为

$c=w^{T}x_{i}+b$

w 为超平面c 的法向量，即垂直于超平面的向量，它能决定超平面的方向。b就是截距，能确定超平面的位置
设置支持向量平面为：

$a:w^{T}x_{1}+b=1$

$b:w^{T}x_{2}+b=-1$

求margin：

a上有一点x1，b上有一点x2，原点为O， $\vec{x_{1}}$ 的表示为（x1-O）， $\vec{x_{2}}$ 的表示为（x2-O），所以可以得到（ $\vec{x_{1}}-\vec{x_{2}}$ ）为两向量的差，margin可表示为：

$margin=\left \| \vec{x_{1}}-\vec{x_{2}} \right \|cos\theta$

需要使margin得到最大值：

a-b： $w^{T}\cdot \left ( \vec{x_{1}}-\vec{x_{2}} \right )=2$

即 $\left \| w \right \|\cdot \left \| \vec{x_{1}}-\vec{x_{2}} \right \|cos\theta =2$

$margin=\frac{\left \| w \right \|}{2}$

即将求margin最大值问题转为求解w最小值：

将超平面上方标记为1，下方标记为-1，根据已设a，b面可得约束条件为：

$\left\{\begin{matrix} w^{T}x_{i}+b>=1,y_{i}=1 & & \\ w^{T}x_{i}+b<=-1,y_{i}=-1& & \end{matrix}\right.$

$s.t.:y_{i}(w^{T}x_{i}+b)=0$

引入拉格朗日乘子 $\lambda$ ： $F(x,y,\lambda )=f(x,y)+\lambda h(x,y)$ 将问题无约束化

此时要满足KKT条件：

KKT条件：满足所有要求条件

如 $argmin\frac{1}{2}\left \| w \right \|^{2}$

$s.t.:y=(w^{T}x_{i}+b)>=0$ i=1,2,3...,m i的取值范围为1-m即需要满足m个条件

拉格朗日：

①

$L(w,b,\lambda )=\frac{1}{2}\left \| w \right \|^{2}-\sum_{i=1}^{m}\lambda _{i}(y_{i}(w^{T}x_{i}+b)-1) -\sum_{i=1}^{m}\lambda _{i}(y_{i}(w^{T}x_{i}+b))+\sum_{i=1}^{m}\lambda _{i}$

②

$\frac{\partial L}{\partial w}=w-\sum_{i=1}^{m}\lambda _{i}y_{i}x_{i}=0$

$\frac{\partial L}{\partial b}=-\sum_{i=1}^{m}\lambda _{i}y_{i}=0$

③带回第一步求 $\lambda$ 最小值：

可得最终模型 $f(x)=w^{T}x_{i}+b=\sum_{i=1}^{m}\lambda _{i}y_{i}x^{T}_{i}x_{i}+b$

对于KKT条件需要满足:

$1.\lambda _{i}>=0$

$2.y_{i}f(x_{i})>=1$

$3.\lambda _{i}(y_{i}f(x_{i})-1)=0$

由此可得

若 $y_{i}f(x_{i})=1\Rightarrow \lambda _{i}!=0$ 只与支持向量上点有关

若 $y_{i}f(x_{i})>1\Rightarrow \lambda _{i}=0$ 不在最大边界点上

3、求解问题——SMO

算法流程：每次选取两个 $\lambda$ 进行更新，固定其余参数，对偶求解 $\lambda _{ij}$ 直至收敛

计算方法也为引入拉格朗日算子满足KKT条件进行求解，即不多赘述。

4、核函数

Mercer定理：只要对称函数值所对应的核函数半正定，则为核函数

为什么会用到核函数?

用于解决线性不可分问题，将线性不可分的函数进行升维到高维可分函数。

如 $ax_{1}^{2}+bx_{2}^{2}+cx_{1}x_{2}=1$

映射为： $w _{1}z_{1}+w_{2}z_{2}+w_{3}z_{3}+b=0$

$\varnothing :R_{2} \to R_{3}$ $(x_{1},x_{2})\leftrightarrow (z_{1},z_{2},z_{3}):=(\sqrt{x_{1}^{2}},\sqrt{2}x_{1}x_{2},\sqrt{x_{2}^{2}})$

基本思想为将x映射为 $\varnothing(x)$ ，处理过程同二维，仅 $x^{T}_{i}x_{j}$ 与 $\varnothing (x_{i})^{T}\varnothing (x_{j})$ 不同，其余都相同计算过程，即不多赘述。

5、SVM 算法特性

1、训练好的模型的算法复杂度是由支持向量的个数决定的，而不是由数据的维度决定的。所以 SVM 不太容易产生过拟合。
2、SVM 训练出来的模型完全依赖于支持向量，即使训练集里面所有非支持向量的点都被去除，重复训练过程，结果仍然会得到完全一样的模型。
3、一个 SVM 如果训练得出的支持向量个数比较少，那么SVM 训练出的模型比较容易被泛化。

二、利用SVM进行线性回归分类

代码：

import numpy as np
import matplotlib.pyplot as plt 
from scipy import stats

# 引入数据集，并可视化
from sklearn.datasets._samples_generator import make_blobs
X, y = make_blobs(n_samples=50, centers=2,
                  random_state=0, cluster_std=0.60)
# plt.figure(figsize=(8,8))
# plt.scatter(X[:, 0], X[:, 1], c=y, s=50)

散点图：

#要完成一个分类问题，需要在2种不同的样本点之间产出一条“决策边界”，下图显示了3条不同的可选决策边界。
xfit = np.linspace(-1, 3.5)
plt.figure(figsize=(8,8))

plt.scatter(X[:, 0], X[:, 1], c=y, s=50)

for k, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
#     print('k \t'+str(k))
#     print('b \t'+str(b))
#     print("-------------")
    
    plt.plot(xfit, k * xfit + b, '-k')

plt.xlim(-1, 3.5)

#拟合支持向量机，这是一个线性可切分的例子，用sklearn中linear kernel的svm来分一下。
#构建一个线性SVM分类器
from sklearn.svm import SVC # "Support Vector Classifier"

clf = SVC(kernel='linear')
clf.fit(X, y)

# 可视化函数
def plot_svc_decision_function(clf, ax=None):
    """Plot the decision function for a 2D SVC"""
    if ax is None:
        ax = plt.gca()
    x = np.linspace(plt.xlim()[0], plt.xlim()[1], 30)
    y = np.linspace(plt.ylim()[0], plt.ylim()[1], 30)
    Y, X = np.meshgrid(y, x)
    P = np.zeros_like(X)
    for i, xi in enumerate(x):
        for j, yj in enumerate(y):
            P[i, j] = clf.decision_function([[xi, yj]])
    # plot the margins
    ax.contour(X, Y, P, colors='k',
               levels=[-1, 0, 1], alpha=0.5,
               linestyles=['--', '-', '--'])

plt.figure(figsize=(8,8))
plt.scatter(X[:, 0], X[:, 1], c=y, s=50)
plot_svc_decision_function(clf)
plt.show()

分类结果：