在结构光三维重建中，典型的方法为条纹投影轮廓术（Fringe Projection Profilometry, FPP），其主要步骤如下：

本文主要介绍相位解调和相位展开两部分。

一、相位解调

标准的 N 步相移法能够消除环境光和表面反射率的干扰，对系统的随机噪声具有一定的抑制作用，具有较高的测量分辨率和精度， 是使用最多的一种结构光测量方法。标准的 N 步相移模型可以表示为：

 其中(x,y)表示二维像素点，I(x,y)表示图像像素的强度，A(x,y)表示背景光强，B(x,y)表示调制光强， 与被测物体表面的反射率有关，i为相移步数，i=0,1,2...N-1，(x,y)为像素点的相位值，可通过下式计算得到：

 由于式中有A(x,y)、B(x,y)、(x,y)三个未知量，因此至少需要三幅相移图像才能求解，即最少为三步相移法。

二、相位展开

上述N步相移法采用arctan函数计算相位，得到的相位在[]之间（之所以不是[-, ]是因为使用的是opencv里atan2函数，感兴趣可以查一下这个函数），这会导致得到的相位是不连续的，如下图所示：

而我们的目的是得到图像中每个点的绝对相位值，因此要消除这种不连续，此时就要进行相位展开。

相位展开方法分为空间相位展开方法和时间相位展开方法：

1.空间相位展开方法通过法通过局部或全局优化利用邻域点相位来展开每一点的相位，受到表面平滑假设的限制，即只能恢复相对相位，当视场包含不连续或孤立的物体时，空间相位展开将会失败；

2.时间相位展开通过分析时间序列上相位的变化来确定每个像素点的条纹级数，而不依赖于相位图上其他点的相位值，因此可以得到绝对的相位分布。

因此通常采用时间相位展开方法，主要有多频外差相位展开算法。

多频外差相位展开算法的原理来源于多波长干涉技术，简单来说就是两个不同波长的光的干涉结果进行作差合成，得到一个新的等效波长的光干涉结果，将波长转化为条纹的周期，即可表述为将两个不同周期的条纹进行做差合成，从而得到一个新的等效周期的条纹，且新条纹的频率为两个条纹的频率之差，如果选取合适频率的条纹，使两频率之差为1，也就是在整个图像范围内仅有一个周期，合成过程可表示为：

然后再利用该合成条纹对原相位函数按下式进行展开：

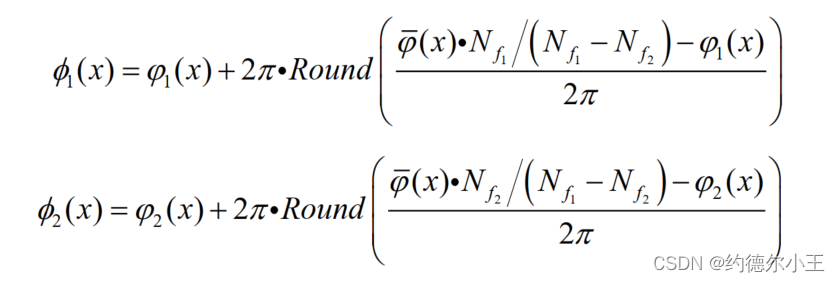
式中Nf表示条纹数量也即是条纹频率，Round表示四舍五入取整，从而得到连续递增的绝对相位，如下图所示：

 三、代码实现（以三频四步为例）

/*生成条纹函数******************************************************************************
f:条纹频率；
w：图片尺寸；
N：相移步数；
direction：条纹方向，0：竖条纹，其他：横条纹，默认竖条纹；
*/
vector<Mat> creatP(float f,Size w,int N,int direction=0) {
	vector<Mat>imgs;
	for (int k = 0; k < N; k++) {
		Mat img=Mat::zeros(w.height, w.width, CV_8UC1);
		int a = direction == 0 ? w.height : w.width;
		int b = direction == 0 ? w.width : w.height;
		for (int i = 0; i < a; i++) {
			for (int j = 0; j < b; j++) {
				if(direction==0)img.at<uchar>(i, j) = 
                    128 + 127 * cos(2 * pi * f * j / w.width + 2 * pi * k / N);
				else img.at<uchar>(j, i) = 
                    128 + 127 * cos(2 * pi * f * j / w.width + 2 * pi * k / N);
			}
		}
		imgs.push_back(img);
	}
	return imgs;
}

/*合并图像函数****************************************************************************
c_f：竖条纹频率；
r_f:横条纹频率；
N：相移步数；
*/
vector<Mat>combineImags(vector<int>& c_f, vector<int>& r_f, Size z, int N){
	vector<Mat>imgs;
	for (int direction = 0; direction < 2; direction++) {
		vector<int>f = direction == 0 ? c_f : r_f;
		for (int i = 0; i < f.size(); i++) {
			for (int j = 0; j < N; j++)imgs.push_back(creatP(f[i], z, N,direction)[j]);
		}
	}
	return imgs;
}

/*相位展开函数****************************************************************************
imgs:三频四步图像共12张；
p：要计算绝对相位的点；
*/
vector<double> caculatePhase(vector<Mat>& imgs, Point p){
	vector<int>PointValues;
	vector<double>phase,u_phase;
	double ph12, ph23, ph123;
	for (int a = 0; a < 2; a++) {
		vector<int> f = a == 0 ? c_frequency : r_frequency;
		for (int i = 0; i < f.size(); i++) {
			for (int j = 1; j < N+1; j++)
                PointValues.push_back(imgs[12*a+4*i+j].at<uchar>(p));
			phase.push_back(atan2(PointValues[12 * a + 4 * i + 3] - 
                            PointValues[12 * a + 4 * i + 1], 
                            PointValues[12 * a + 4 * i] -
                            PointValues[12 * a + 4 * i + 2]));
		}
		ph12 = phase[3 * a] > phase[3 * a + 1] ? 
                              phase[3 * a] - phase[3 * a + 1] : 
                              phase[3 * a] - phase[3 * a + 1] + 2 * pi;
		ph23 = phase[3 * a + 1] > phase[3 * a + 2] ? 
                                  phase[3 * a + 1] - phase[3 * a + 2] : 
                                  phase[3 * a + 1] - phase[3 * a + 2] + 2 * pi;
		ph123 = ph12 > ph23 ? ph12 - ph23 : ph12 - ph23 + 2 * pi;

		phase[3 * a + 1] = ph12 + 2 * pi * round((ph123 * (f[0] - f[1]) - ph12) / 2 / pi);
		phase[3 * a] = phase[3 * a] + 2 * pi * round((phase[3 * a + 1] * f[0] / (f[0] - f[1]) - phase[3 * a]) / 2 / pi);
		u_phase.push_back(phase[3 * a]);
	}
	return u_phase;
}复制

如有问题，欢迎讨论交流！

推荐内容