LQR控制算法的浅析

路在脚下，梦在心里

5406人浏览 · 2022-09-10 16:08:35

路在脚下，梦在心里 · 2022-09-10 16:08:35 发布

3.2.1、开环情况（k1=k2=0，初值设置为5）

前言

这里的部分内容和之前的转载文章有相同的地方LQR控制算法及matlab/simulink仿真_陌路两立的博客-CSDN博客_lqr matlab，写这篇文章的目的是为了增强自己对LQR控制算法的理解。

一、知识点补充

1、拉格朗日乘子法

假设需要求极值的目标函数为 $f(x,y)$ ，约束条件为 $\varphi(x,y)=M$ 。设 $g(x,y)=M-\varphi(x,y)$ ，定义一个新函数 $F(x,y)=f(x,y)+\lambda g(x,y)$ ，则用偏导数方法列出方程：

$\begin{aligned} \frac{\partial F}{\partial x}=0;\\ \\\frac{\partial F}{\partial y}=0;\\ \\ \frac{\partial F}{\partial \lambda}=0; \end{aligned}$

2、积分中值定理

若函数 $f(x,y)$ 在闭区间 $[a,b]$ 上连续，则在积分区间 $[a,b]$ 上至少存在一个点 $\varepsilon$ ，使得下式成立：

$\int_{a}^{b} f(x) dx=f(\varepsilon )(b-a)$

其中， $a,b,\varepsilon$ ，满足： $a\leqslant \varepsilon \leqslant b$ 。

3、向前欧拉法，向后欧拉法，中点欧拉法

向前欧拉法： $x(\varepsilon )=x(t)$ ；

向后欧拉法： $x(\varepsilon )=x(t+dt)$ ；

中点欧拉法： $x(\varepsilon )=\tfrac{x(t)+x(t+dt)}{2}$ 。

4、向量的导数

$\begin{aligned} \frac{\partial x^TA}{\partial x}&=A;\\ \frac{\partial x^TAx}{\partial x}&=(A^T+A)x;\\ \frac{\partial Ax}{\partial x}&=A^T \end{aligned}$

参考：向量的导数_影子飞扬的博客-CSDN博客_向量的导数

5、矩阵求逆引理(记住就好，推导见链接)

$(A+BCD)^{-1}=A^{-1}-A^{-1}B(C^{-1}+DA^{-1}B)^{-1}DA^{-1}$

参考：矩阵求逆引理(matrix inversion lemma)_UESTC_C2_403的博客-CSDN博客_矩阵求逆引理

二、连续时间下的LQR推导

1、系统状态方程

开环： $\dot{x}=Ax$ ;

闭环： $\dot{x}=Ax+Bu$ ，设计 $u=-kx=-(k_1,k_2,\cdots)\begin{pmatrix} x_1\\x_2\\\vdots \end{pmatrix}$ ，可以得到 $\dot{x}=Ax-Bkx=(A-Bk)x$ ,通过改变 $k$ 可以改变 $A-Bk$ 的特征值从而控制系统表现。

2、推导过程

系统的状态发生变化的原因是在上一个状态时，有外界干扰或者系统的输入发生变化引起的，忽略外界干扰的影响，这里引入cost function(能量函数，损失函数)：

$J=\int_{0}^{\infty }(x^TQx+u^TRu) dt$

其中，Q和R均为自己设计的半正定矩阵。我们的目的就是通过设计Q和R使得能量函数最小。

能量函数的理解：

Q= $\begin{equation} \begin{bmatrix} a & & & \\ & b & & \\ & & c&\\ & & &\ddots \end{bmatrix} \end{equation}$ ,能量函数前面部分可以写成 $\color{red}ax_1^2+bx_2^2+cx_3^2+\dots$ ，当 $\color{red}x\neq0$ 时，Q表现为惩罚；R越大，u对J的影响越大，希望J越小，可以使得u减小。

假设Q= $\begin{equation} \begin{bmatrix} 100 & & & \\ & 1 & & \\ & & 1&\\ & & &\ddots \end{bmatrix} \end{equation}$ ，当 $\color{red}x_1\neq0$ 时，J将会变得非常大， $\color{red}x_1$ 对J有较大的影响，为了使得J减小，只能希望 $\color{red}x_1$ 快速收敛。

将控制器 $u=-kx$ 代入到能量函数中：

$J=\int_{0}^{\infty }(x^TQx+(-kx)^TR(-kx)) dt =\int_{0}^{\infty }x^T(Q+k^TRk)xdt$

为了找到 $k$ ,假设存在一个常量矩阵 $P$ ，使得

$\frac{\mathrm{d} }{\mathrm{d} t}x^TPx=-x^T(Q+k^TRk)x$

随后得到：

$\dot{x}^TPx+x^TP\dot{x}+x^T(Q+k^TRk)x=0$

将 $\dot{x}=Ax-Bkx=(A-Bk)x$ 代入到上式中得：

$\begin{aligned} ((A-Bk)x)^TPx+x^TP(A-Bk)x+x^T(Q+k^TRk)x &=x^T(A-Bk)^TPx+x^TP(A-Bk)x+x^T(Q+k^TRk)x\\ &=x^T((A-Bk)^TP+P(A-Bk)+(Q+k^TRk))x\\&=0 \end{aligned}$

为了使上式恒成立，我们可以得到：

$\begin{aligned} (A-Bk)^TP+P(A-Bk)+Q+k^TRk=0\\ \Rightarrow A^TP+PA+Q+k^TRk-k^TB^TP-PBk=0 \end{aligned}$

通过令 $k=R^{-1}B^TP$ ，上式可以化简为：

$A^TP+PA+Q-PBk=0\Rightarrow A^TP+PA+Q-PBR^{-1}B^TP=0$

该式就是著名的Riccati方程。其中 $A,B$ 是系统矩阵已知，选取合适的 $Q,R$ ，可以解出 $P$ ，从而得到 $k$ ，控制器 $u=-kx$ 。

注：k的由来

$k^TRk-k^TB^TP=k^T(Rk-B^TP)=0$

$Rk-B^TP=0\Rightarrow k=R^{-1}B^TP$

3、例子-------手平衡小杆

3.1、系统模型

下面是B站大佬DR_CAN对LQR控制算法的讲解（知识的搬运工）。

运动学方程：

$\ddot{\phi}=\tfrac{g}{L}\phi-\tfrac{1}{L}\ddot{\delta }$

其中： $L$ 表示杆子的长度， $g$ 表示重力加速度， $\phi$ 表示杆子与垂直方向的夹角， $\delta$ 表示手的移动。

通过令 $x_1=\phi, \quad x_2=\dot{\phi}, \quad u=\tfrac{1}{L}\ddot{\delta}$ 可以得到：

$\begin{aligned} \dot{x}_1&=x_2\\ \dot{x}_2&=\tfrac{g}{L}x_1-u \end{aligned}$

令 $L=1, \quad g=10$ 得：

$\begin{aligned} &\begin{pmatrix} \dot{x}_1\\ \dot{x}_2 \end{pmatrix} =\begin{pmatrix} 0&1\\ 10&0 \end{pmatrix}\begin{pmatrix}x_1\\x_2 \end{pmatrix}+\begin{pmatrix} 0\\-1\end{pmatrix}u\\ &u=-kx=-(k_1,k_2)\begin{pmatrix} x_1\\x_2\end{pmatrix}=-k_1x_1-k_2x_2 \end{aligned}$

3.2、simulink模型仿真

3.2.1、开环情况（k1=k2=0，初值设置为5）

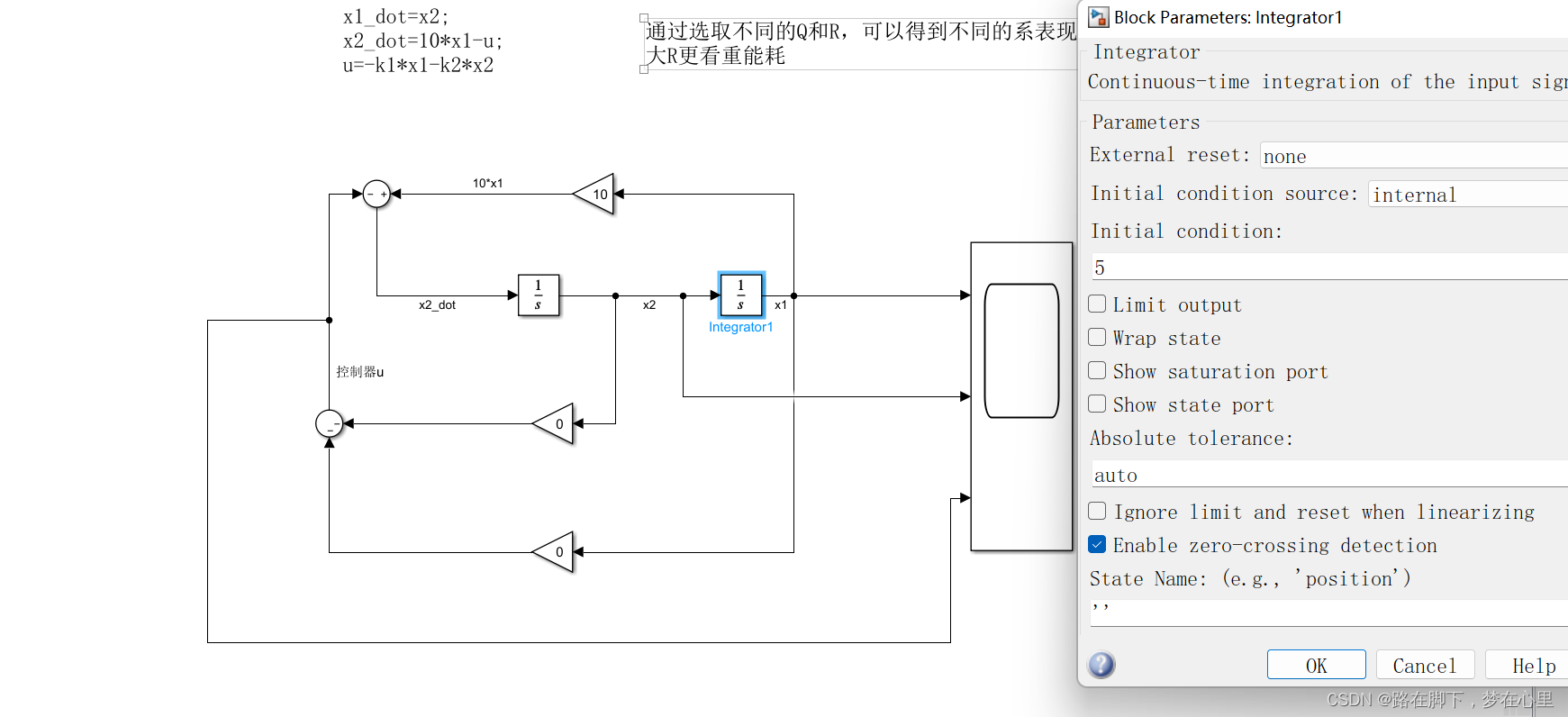
3.2.2、闭环情况

LQR求k代码：

%% 系统参数
A=[0 1;10 0];
B=[0;-1];

%% 大Q情况
Q=[100 0;0 1];
R=.01;
K=lqr(A,B,Q,R);

%% 大R情况
% Q=[1 0;0 1];
% R=100;
% K=lqr(A,B,Q,R);


%% 求解出来
k1=K(1,1);
k2=K(1,2);

simulink模型：

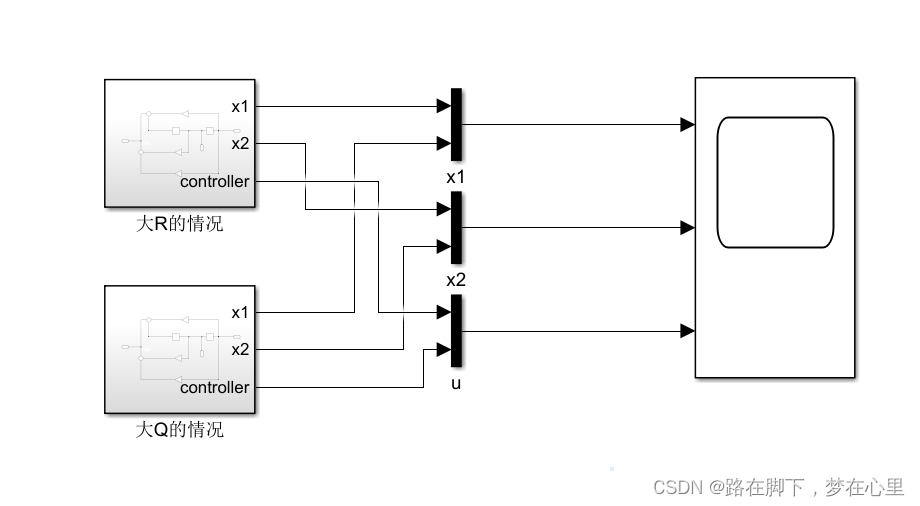
大R情况：k1=-20.000499987499590，k2=-6.325424884938331；

大Q情况：k1=-1.104987562112088e+02，k2=-17.916403445513760；

仿真结果：

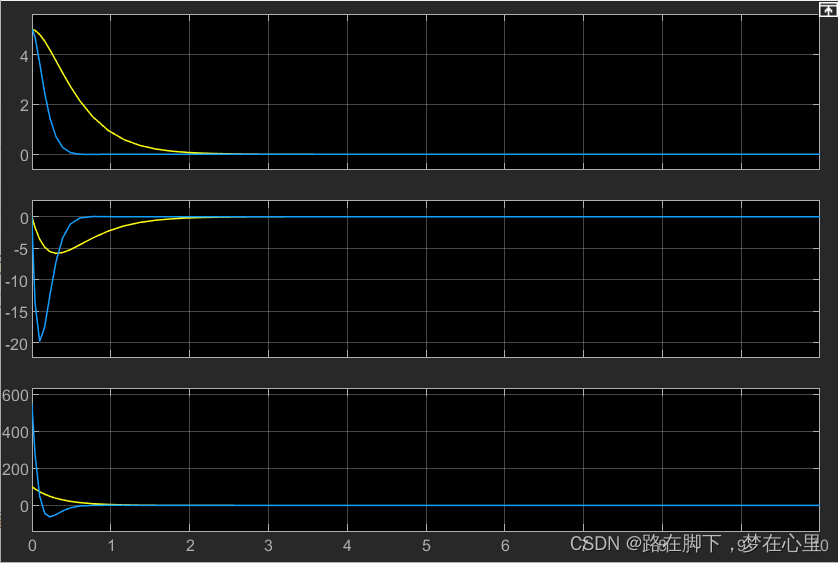
结论：通过选取不同的Q和R可以得到不同的系统表现，其中大Q决定的是系统的状态能否快速达到收敛效果，大R决定的是系统的能耗(输入)。

参考： 1、视频链接：https://www.bilibili.com/video/BV1RW411q7FDshare_source=copy_web

2、LQR控制算法及matlab/simulink仿真_陌路两立的博客-CSDN博客_lqr matlab

三、离散时间下的LQR推导（重要）

1、状态方程离散化

离散之后最重要的一个就是不可以使用微分方程描述系统了。

动力学方程： $\dot{x}=Ax+Bu$ ,对动力学方程两边同时求积分得：

$\begin{aligned} \int_{t}^{t+dt} \dot{x} dt&=\int_{t}^{t+dt} (Ax+Bu)dt\Rightarrow \\ x(t+dt)&=x(t)+Ax(\xi )dt+Bu(\xi )dt, \quad\xi\in (t,t+dt) \Rightarrow \\ x(t+dt)&=x(t)+A\times\tfrac{x(t)+x(t+dt)}{2}dt+Bu(t)dt\Rightarrow \\ x(t+dt)&=(I-\tfrac{Adt}{2})^{-1}(I+\tfrac{Adt}{2})x(t)+(I-\tfrac{Adt}{2})^{-1}Bu(t)dt\\ &\approx (I-\tfrac{Adt}{2})^{-1}(I+\tfrac{Adt}{2})x(t)+Bu(t)dt\\\\ x_{k+1}&=\bar{A}x_k+\bar{B}u_k \end{aligned}$

其中 $\bar{A}=(I-\tfrac{Adt}{2})^{-1}(I+\tfrac{Adt}{2}),\quad \bar{B}=Bdt$ ，这里我们需要知道是 $x_{k+1}$ 是 $n \times1$ 维的， $dt$ 称为采样周期。

使用到的知识点：状态 $x$ 去 $\xi$ 使用的是中间欧拉法，控制输入 $u$ 去 $\xi$ 使用的是向前欧拉法(因为我们无法知道 $u(t+dt)$ )。

2、离散LQR的解法

step 1：和连续时间下的LQR相同，首先引入能量函数(cost function)：

$J=\sum_{k=0}^{n-1}(x_k^TQx_k+u_k^TRu_k)+x_n^TQx_n$

step 2：引入约束函数：

$\begin{aligned} \begin{matrix} \bar{A}x_0+\bar{B}u_0-x_1=0\\ \bar{A}x_1+\bar{B}u_1-x_2=0\\ \vdots \\ \bar{A}x_{n-1}+\bar{B}u_{n-1}-x_n=0\\ \end{matrix} \end{aligned}$

注：为什么cost function只有 $\color{red}{x_n^TQx_n}$ ，却没有 $\color{red}u_n^TRu_n$ 呢？

答：如果 $\color{red}J$ 改为 $\color{red}J=\sum_{k=0}^{n-1}(x_k^TQx_k+u_k^TRu_k)+x_n^TQx_n+u_n^TRu_n$ 的话，可是约束函数只能覆盖 $\color{red}u_0 \sim u_{n-1}, x_0 \sim x_n$ ，所以cost function只能为 $\color{red}J=\sum_{k=0}^{n-1}(x_k^TQx_k+u_k^TRu_k)+x_n^TQx_n$ 。

step 3：拉格朗日乘子法求解cost function：

首先将约束函数写为：

$\begin{aligned} \bar{A}\begin{pmatrix} x_0\\x_1\\ \vdots \\x_{n-1}\end{pmatrix}_{n\times 1} +\bar{B}\begin{pmatrix} u_0\\u_1\\ \vdots \\u_{n-1}\end{pmatrix}_{n\times 1}- \begin{pmatrix} x_1\\x_2\\ \vdots \\x_{n}\end{pmatrix}_{n\times 1}=\begin{pmatrix} 0\\0\\ \vdots \\0\end{pmatrix}_{n\times 1} \end{aligned}$

然后构造新函数：

$\begin{aligned} F&=\sum_{k=0}^{n-1}(x_k^TQx_k+u_k^TRu_k)+x_n^TQx_n+\sum_{k=0}^{n-1}\lambda_{k+1}^T(\bar{A}x_k+\bar{B}u_k-x_{k+1})\\ &=\sum_{k=0}^{n-1}(x_k^TQx_k+u_k^TRu_k+\lambda_{k+1}^T(\bar{A}x_k+\bar{B}u_k)-\lambda_{k+1}^Tx_{k+1})+x_n^TQx_n\\ &=\sum_{k=0}^{n-1}(H_k-\lambda_{k+1}^Tx_{k+1})+x_n^TQx_n\\ &=\sum_{k=0}^{n-1}(H_k-\lambda_k^Tx_k)+x_n^TQx_n-\lambda_n^Tx_n+\lambda_0^Tx_0 \end{aligned}$

其中 $H_k=x_k^TQx_k+u_k^TRu_k+\lambda_{k+1}^T(\bar{A}x_k+\bar{B}u_k)$ 。

注：注意这里的维度问题， $\color{red}\bar{A}x_k+\bar{B}u_k-x_{k+1}$ 是 $\color{red}n\times1$ 维的。

接下来对构造的函数求偏导：

首先对 $x$ 求偏导：

$\begin{aligned} \begin{matrix} \frac{ \partial F }{ \partial x_0 }=0 \Rightarrow \frac{ \partial F }{ \partial x_0 }=\frac{\partial H_0}{\partial x_0}-\lambda_0+\lambda_0=0\\ \frac{ \partial F }{ \partial x_1 }=0 \Rightarrow \frac{ \partial F }{ \partial x_1 }=\frac{\partial H_1}{\partial x_1}-\lambda_1=0\\ \frac{ \partial F }{ \partial x_2 }=0 \Rightarrow \frac{ \partial F }{ \partial x_2 }=\frac{\partial H_2}{\partial x_2}-\lambda_2=0\\ \vdots\\ \frac{ \partial F }{ \partial x_{n-1} }=0 \Rightarrow \frac{ \partial F }{ \partial x_{n-1} }=\frac{\partial H_{n-1}}{\partial x_{n-1}}-\lambda_{n-1}=0\\ \end{matrix} \Rightarrow \begin{aligned} \begin{matrix} \lambda_0=\frac{\partial H_0}{\partial x_0}=0\\ \lambda_k=\frac{\partial H_k}{\partial x_k} \quad (k=1 \dots n-1)\end{matrix} \end{aligned}\end{aligned}$

$\frac{ \partial F }{ \partial x_n }=0 \Rightarrow \frac{\partial (x_n^TQx_n-\lambda_n^Tx_n)}{\partial x_n}=0 \Rightarrow \lambda_n=2Qx_n$

$\frac{ \partial H_k }{ \partial x_k }=\frac{ \partial (x_k^TQx_k+u_k^TRu_k+\lambda_{k+1}^T(\bar{A}x_k+\bar{B}u_k)) }{ \partial x_k }=2Qx_k+\bar{A}^T\lambda_{k+1}$

综上所述：

$\begin{aligned} \begin{matrix} \lambda_0=\frac{\partial H_0}{\partial x_0}=0\\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\lambda_k=\frac{\partial H_k}{\partial x_k}=2Qx_k+\bar{A}^T\lambda_{k+1}\quad(k=1 \dots n-1)\\ \lambda_n=2Qx_n \end{matrix} \end{aligned}$

然后对 $u$ 求导：

$\begin{aligned} \begin{matrix} \frac{\partial F}{\partial u_k}=0 \Rightarrow \frac{\partial H}{\partial u_k}=0 \quad (k=1, 2,\dots,n-1) \end{matrix} \end{aligned}$

$\frac{ \partial H_k }{ \partial u_k }=\frac{ \partial (x_k^TQx_k+u_k^TRu_k+\lambda_{k+1}^T(\bar{A}x_k+\bar{B}u_k)) }{ \partial u_k }=2Ru_k+\bar{B}^T \lambda_{k+1}=0$

$u_k=-\frac{1}{2}R^{-1}\bar{B}^T \lambda_{k+1}$

最后对 $\lambda$ 求导：

$\begin{aligned} \begin{matrix} \frac{\partial F}{\partial \lambda_k}=0 \Rightarrow \frac{\partial F}{\partial \lambda_k}=\frac{\partial H_k}{\partial \lambda_k}-x_k=0 \quad (k=1, 2,\dots,n-1) \end{matrix} \end{aligned}$

$\begin{aligned} &\frac{ \partial H_k }{ \partial \lambda_k }-x_k\\ &=\frac{\partial H_{k+1}}{\partial\lambda_{k+1}}-x_{k+1} \\&=\frac{ \partial (x_k^TQx_k+u_k^TRu_k+\lambda_{k+1}^T(\bar{A}x_k+\bar{B}u_k)) }{ \partial \lambda_k }-x_{k+1} \\&=\bar{A}x_k+\bar{B}u_k-x_{k+1}=0\end{aligned}$

$x_{k+1}=\bar{A}x_k+\bar{B}u_k$

综上所述：

$\begin{aligned} \lambda_k&=2Qx_k+\bar{A}^T\lambda_{k+1}\quad\\ \lambda_n&=2Qx_n\\ u_k&=-\frac{1}{2}R^{-1}\bar{B}^T \lambda_{k+1}\\ x_{k+1}&=\bar{A}x_k+\bar{B}u_k \end{aligned}$

其中， $k=1,2,\dots,n-1$ 。

step 4：递推式

当 $k=n-1$ 时：

$\begin{aligned} u_{n-1}=-\frac{1}{2}R^{-1}\bar{B}^T \lambda_{n}=-\frac{1}{2}R^{-1}\bar{B}^T \times 2Qx_n=-R^{-1}\bar{B}^T Qx_n\\ \end{aligned}$

$x_{n}=\bar{A}x_{n-1}+\bar{B}u_{n-1}=\bar{A}x_{n-1}-\bar{B}R^{-1}\bar{B}^T Qx_n\\ \Rightarrow x_n=(I+\bar{B}R^{-1}\bar{B}^T Q)^{-1}\bar{A}x_{n-1}$

$\begin{aligned} \lambda_{n-1}&=2Qx_{n-1}+\bar{A}^T\lambda_{n}\\&=2Qx_{n-1}+2\bar{A}^TQx_n\\&=2Qx_{n-1}+2\bar{A}^TQ(I+\bar{B}R^{-1}\bar{B}^T Q)^{-1}\bar{A}x_{n-1}\\&=2(Q+\bar{A}^TQ(I+\bar{B}R^{-1}\bar{B}^T Q)^{-1}\bar{A})x_{n-1} \end{aligned}$

通过对比 $\lambda_n$ 和 $\lambda_{n-1}$ 可以推出：

$\lambda_k=2P_kx_k \quad (k=1,2,\dots,n)$

其中 $P_k=Q+\bar{A}P_k(I+\bar{B}R^{-1}\bar{B}^TP_k)^{-1}\bar{A}$ (Riccati方程)。

$\begin{aligned} u_k&=-\frac{1}{2}R^{-1}\bar{B}^T \lambda_{k+1}\\&=-\frac{1}{2}R^{-1}\bar{B}^T\times 2P_{k+1}x_{k+1}\\&=-R^{-1}\bar{B}^TP_{k+1}x_{k+1}\\&=-R^{-1}\bar{B}^TP_{k+1}(\bar{A}x_k+\bar{B}u_k) \end{aligned}$

可以得到：

$\begin{aligned} u_k&=-(I+R^{-1}\bar{B}^TP_{k+1}\bar{B})^{-1}R^{-1}\bar{B}^TP_{k+1}\bar{A}x_k \\&=-(R+\bar{B}^TP_{k+1}\bar{B})^{-1}\bar{B}^TP_{k+1}\bar{A}x_k \end{aligned}$

其中 $x_k$ 认为已知。

LQR控制实际为：

首先，取矩阵 $P$ 初值为 $P_n=Q$ ，然后，代入离散时间下的Riccati方程 $P_{k-1}=Q+\bar{A}^TP_k\bar{A}-\bar{A}P_k\bar{B}(R+\bar{B}^TP_{k+1}B)^{-1}\bar{B}^TP_k\bar{A}$ 中迭代，求出矩阵 $P$ (一般只需要迭代几十次， $P$ 就会收敛），最后，将 $P$ 代入到 $u$ 中得到 $u$ 。

总结

这里是我自己学LQR控制算法的推导过程，数学原理很大，总结起来就是，通过选取Q和R，然后将A，B，Q，R代入LQR控制算法中（A，B是系统的状态矩阵，认为是已知的），从而得到K，然后将K代入到反馈控制输入 $u=-Kx$ 中，从而得到控制输入 $u$ ，其中Q决定的是收敛速度，R决定的是能耗。因此，我们需要通过选择合适的Q和R使得cost function达到最优。欢迎大家来讨论指正（我的QQ1012154405），一起在控制的海洋中前进！！！