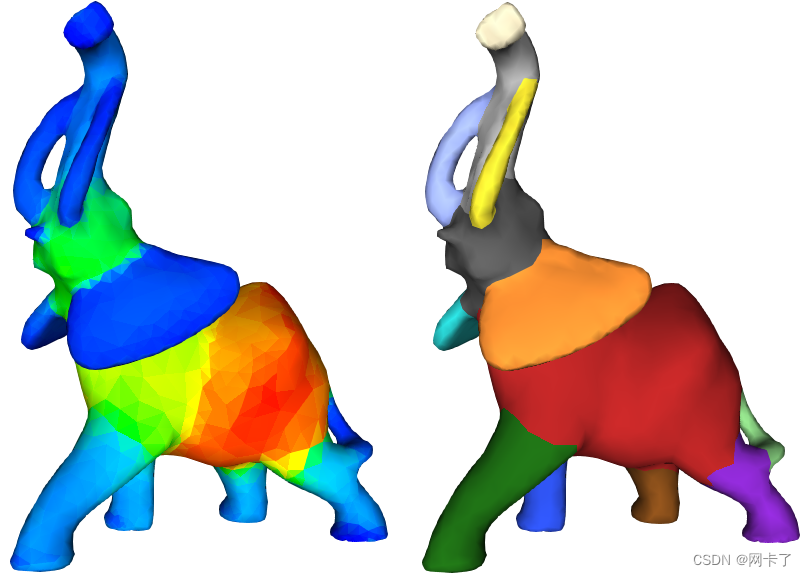
网格分割是将网格分解为更小、更有意义的子网格的过程。该过程用于建模、装配、纹理、形状检索、变形等应用。我们参考了关于网格分割的不同分割技术的综合调查。SDF是Shape Diameter Function的缩写，中文意思是形状直径函数。它是一种测量二维或三维几何形状局部直径的函数，广泛应用于计算机图形学、计算几何和几何计算等领域该软件包提供了一种依赖于形状直径函数的算法实现。给定一个包围三维实体物

缝合允许从一组单独的拓扑元素（面和边）创建连接的拓扑（壳和线）。例如，缝合可用于从单独面的复合体创建壳。区分缝制和其他修改几何形状的工序非常重要，例如填充孔或间隙、粘合、弯曲曲线和曲面等。缝合不会改变形状的几何表示。缝合适用于拓扑元素（面、边），这些元素没有连接，但可以通过几何重合进行连接：它增加了关于拓扑连接的信息。在流形缝合的情况下，已经连接的元素保持不变。让我们定义几个术语：浮动的边不属于任