这个功能已经被qt封装好了，在不同的操作系上封装了不同的方法。在win7上，qt调用的是微软讲述者(microsoft speech)，这个功能在原版win中是自带的，在ghost或者阉割版win中是没有的。需要自己安装。在安装之前，先验证一下你的系统是否可用这个功能：如上图所示，打开控制面板-->文本到语音设置-->语言选择-->预听语音。如果能够正常朗读中文文字，那就说明你的

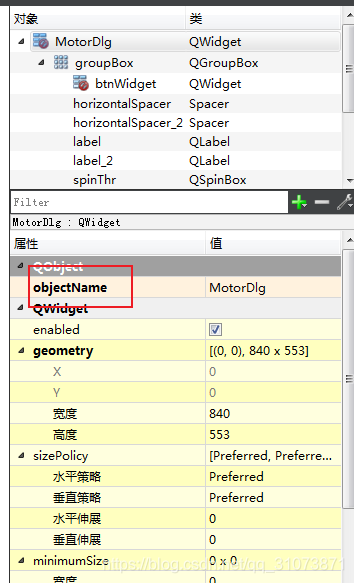
我在ui中拖了一个QWdget作为容器，在里面放入了一个GroupBox，groupBox中又放了几个按钮等，我对最外层的QWidget设置样式表：结果发现，里面所有的子控件、孙子控件的边框都变样了，如何避免这一情况？其实官方帮助手册里已经告诉我们了：就在帮助示例文档中，见下图只要在类名后面用#号串接变量名就行了，修改一下：效果如下，子控件已经不受影响了...

先看两个小知识:1、显示数据散点：ui->customPlot->graph(0)->setScatterStyle(QCPScatterStyle(QCPScatterStyle::ssDisc, 5));//散点2、连接散点的方式：customPlot->graph(0)->setLineStyle(QCPGraph::lsStepLeft);有好几种：折...

设置样式表无非两种方式，1是直接在ui设计师界面填写，这样所见即所得，2是用代码setStylesheet。不过令人困惑的是，经常设置了样式表之后，运行出的结果与预期不符，总结可能有以下原因：1、子控件如果设置了样式表，那么他会把从父控件送来的【同选择器】下的样式表覆盖。注：【样式表选择器】是专业术语，请自行搜索学习。2、子类如果设置了样式表，那么从父类继承来的【同选择器】下的样式表覆盖。注：子类

已知变量X和Y为线性关系（这里XY均为nx1的列向量），为了得知X和Y到底具有怎样的线性关系（也即求解X的系数），如果这是一个工程问题，我们解决这一问题的方法就是对X和Y进行采样，获得很多组样本，然后就能求解出系数了，按照线代的理论，系数矩阵为nxn方阵，且秩为n时，方程具有唯一解，如果采样点过多，也即方程的数目多于未知数的数目，则方程组无解，这时只能求出一个近似解，以不同的目的获得的近似解是不同

所谓频率响应，就是观察一个系统对不同频率的正弦波的响应，我们给系统输入一个幅值为1、频率为ω、相位为0的正弦波以后u(t)=sin(ωt+0)系统也会输出一个正弦波，只是这个正弦波的幅值A、相位φ会发生变化，而ω不会变，也即输出为：y(t)=A(ωt+φ)系统的输出和输入相比，幅值、相位的改变的情况，称为系统的频率响应。（幅频特性、相频特性）求系统的频率响应有3种方法：1、设...

一般有2种方法绘制PCB封装：一、直接建立空文件，二、使用向导一、从空文件建立PCB封装1、依次点击【文件】【新建】【库】【PCB原件库】，起名保存建议在画焊盘之前，先设置下网格间距，步骤如下，①右击绘图区，②栅格属性，③填写网格间距（注：100 mil = 2.54 mm）2、双击上一步新建好的PCB库，然后点击PCB Library选项卡进入PCB原件列表界面：3、在PCB元器件列表中右击，添

对于有C基础的同学来说，学js是相当简单的，语法类似，这里主要列一下两者的异同，基本上记住了这些异同点，就可以使用js了。不过C是编译性语言，js是解释性语言，差别还是不小的。1、js中的变量赋值时，除了基本类型以外，都是赋引用。2、两者都有回调函数的概念，而且函数名就是回调变量名...

任意物体绕自己的各个轴旋转，其【姿态的变化】情况可以用旋转矩阵R来表示。所谓【姿态的变化】情况，可以这样理解：前提：大地坐标系G系与大地固连，物体坐标系B系与飞机固连（X轴的方向为机头方向，Y轴的方向为左翼，Z轴方向朝天），初始状态下，令两个坐标系完全重合。问题：现在我在飞机上任取一点A，该点在大地系的坐标为A0=（x0,y0,z0），（显然此时该点在机体系的坐标是一模一样的），那么当飞机...

做simulink仿真时，我们希望研究某个参数对于系统响应的影响，就需要不断的调整某个模块的参数，为了对比调参前后，系统的响应曲线，我们需要把前后两次的仿真结果，用toWorkspace模块送入工作空间，然后再plot绘图对比。之前我一直是这么干的。今天突然发现，新版simulink里面有了一个新功能，不知道是哪个版本开始的。把鼠标放在响应曲线的通路上，选中下图所示的Enable/Disable