从今天起我想记录下我的学习历程，将成果总结起来，方便日后复习关于MATLAB遗传算法的工具箱文件放在文章末尾需要的自取首先，我先来简单说明下如何将工具箱添加到matlab中去将工具箱文件夹复制到本地计算机中的工具箱目录下，路径为matlabroot\toolbox。其中matlabroot为matlab的安装目录将工具箱所在的文件夹添加到MATLAB的搜索路径中，可以通过调用addpath命令来添

一、理论基础在实际工程优化问题中,多数问题是多目标优化问题。相对于单目标优化问题,多目标优化问题的显著特点是优化各个目标使其同时达到综合的最优值。然而,由于多目标优化问题的各个目标之间的相互影响,多个目标难以同时达到最优,因此，一般适用于单目标问题的方法难以用于多目标问题的求解。多目标优化问题很早就引起了人们的重视，现已经发展出多种求解多目标优化问题的方法。多目标优化问题求解中最重要的概念是非劣解

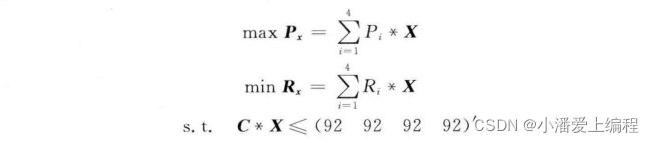
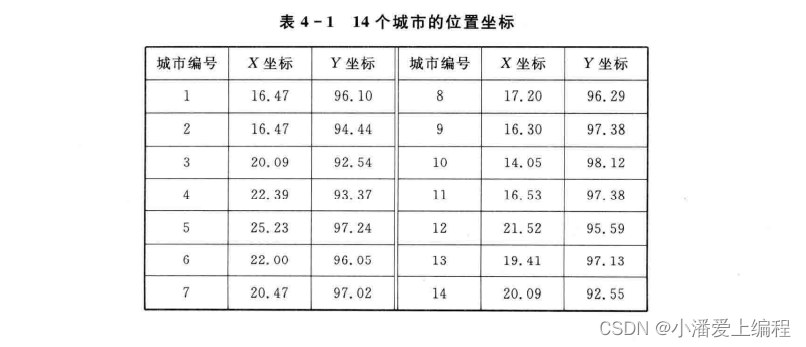
TSP (traveling salesman problem，旅行商问题)是典型的NP完全问题，即其最坏情况下的时间复杂度随着问题规模的增大按指数方式增长，到目前为止还未找到一个多项式时间的有效算法。一、问题描述本案例以14个城市为例，假定14个城市的位置坐标如表4 - 1所列。寻找出一条最短的遍历14个城市的路径。二、解决思路及步骤1、算法流程图2、遗传算法实现及部分代码（1）编码采用整数排列

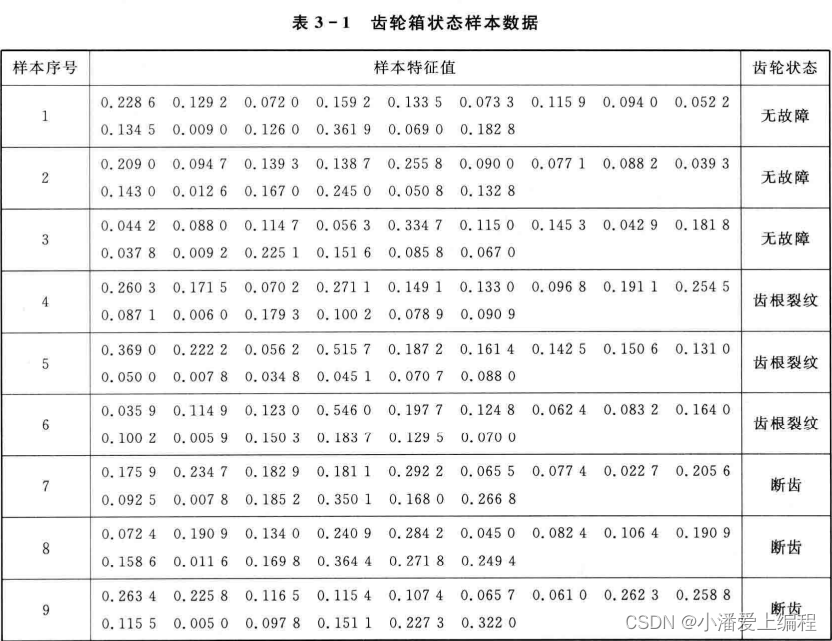
BP网络是前向网络的核心部分，是神经网络中的最精华、最完美的部分，由于其简单的结构，可调整的参数多，训练算法也多，而且可操作性好，BP神经网络获得了非常广泛的应用，但是也存在着一些缺陷，例如学习收敛速度太慢、不能保证收敛到全局最小点、网络结构不易确定。另外，网络结构、初始连接权值和阈值的选择对网络训练的影响很大，但是又无法准确获得，针对这些特点可以采用遗传算法对神经网络进行优化。案例问题描述这里以

一、理论基础多目标优化问题可以描述如下：其中，f(x) 为待优化的目标函数；x 为 待优化的变量；lb 和 ub 分别为变量 x 的下限和上限约束；Aeq * x = beq 为变量 x 的线性等式约束；A * x <= b 为变量 x 的线性不等式约束。在上图所示的优化问题中，目标函数 f1 和 f2 是相互矛盾的。因为 A1 < B1 且 A2 > B2，也就是说，某一个目标

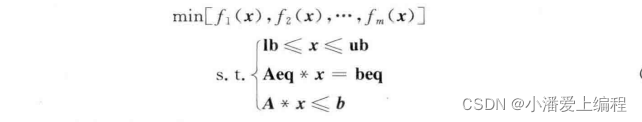
遗传算法是一种借鉴生物界自然选择和进化机制发展起来的高度并行、随机、自适应的全局优化概率搜索算法。由于优化时不依赖于梯度，具有很强的鲁棒性和全局搜索能力，因此，被广泛应用于机器学习，模式识别，数学规划等领域。然而，随着遗传算法的广泛应用以及研究的深入，其诸多缺陷与不足也暴露出来，例如，早熟收敛问题。一、遗传算法的未成熟收敛未成熟收敛是遗传算法中不可忽视的现象，主要表现在群体中的所有个体都趋于同一状