对其进行调整，调整的思路和堆的删除相似，但是要从后往前开始，在左右两个堆中进行调整；从倒数第一个没有儿子的结点开始，即从最后一个非叶子节点开始，依次进行下滤操作，将其子树调整为最大堆。因为最后一个非叶子节点的数组下标为n/2，其中n为堆中元素的个数，所以从i=n/2开始循环。Parent表示当前结点的父结点，Child表示当前结点的子结点，X表示当前结点的值。然后，从要下滤的结点开始，沿着其左右子

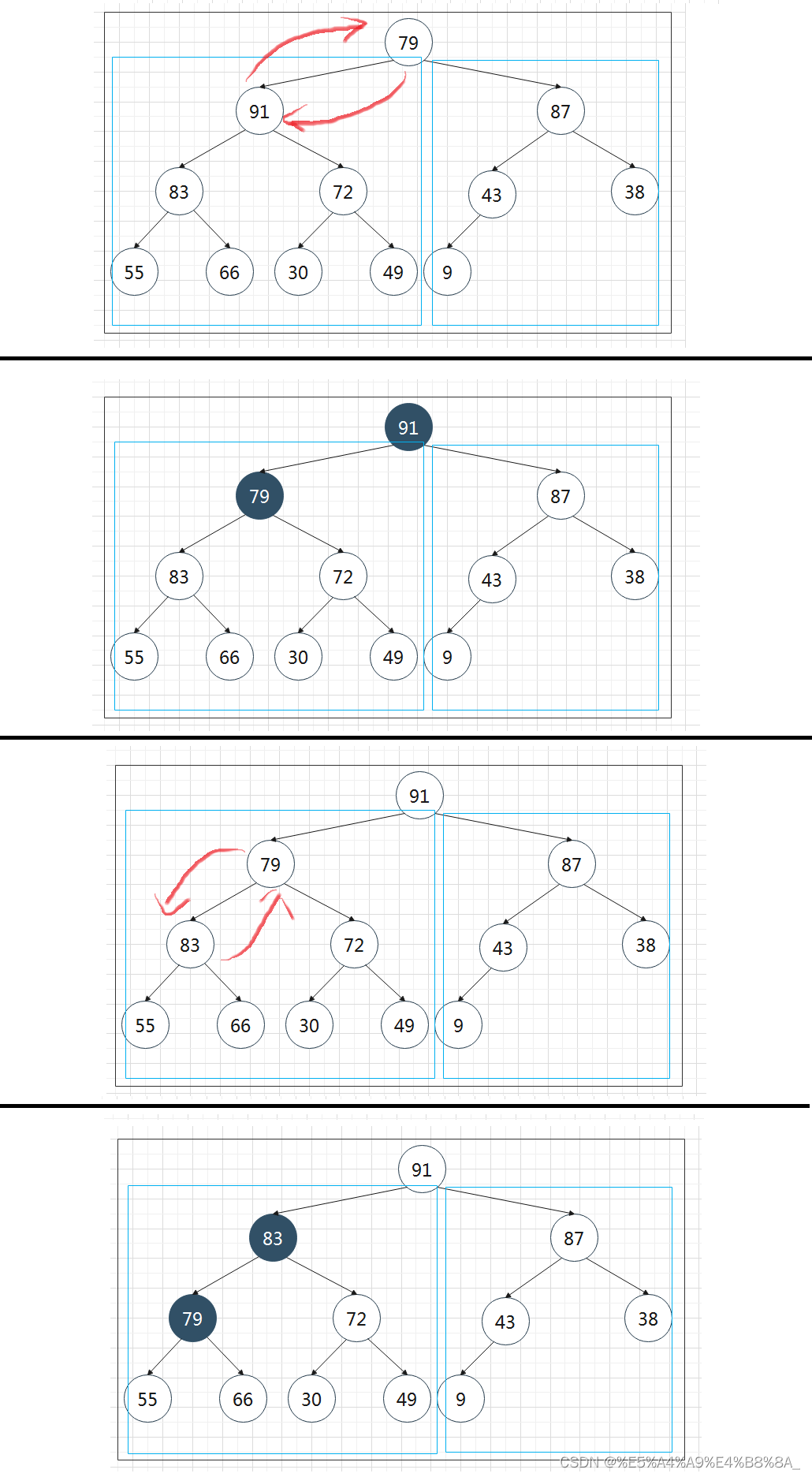
数据结构学习记录——集合及运算（集合的表示、并查集、树结构表示集合、集合运算、查找函数、并运算）交、并、补、差，判定一个元素是否属于某一个集合。在合并两个集合时，根据两个集合的大小来判断将哪个集合并入另一个集合。这样能使得并起来之后的树的高度尽可能小一点。如果集合 1 的大小（S[Root1]）比集合 2 的大小（S[Root2]）小，就将集合 1 并入集合 2 中。此时，需要将集合 1 的根结点

什么是平衡二叉树？以一个例子来解释一下：搜索树结点按不同的插入次序，将会导致不同的深度和平均查找长度ASL在二叉搜索树中查找一个元素：（a）要找到Jan，需要查找一次；要找到Feb，需要查找两次；要找到Mar，也需要查找两次......要找到Nov，需要查找六次。把所有查找次数加起来，再除以12，得到平均查找长度：ASL（a） = （ 1 + 2 * 2 + 3 * 3 + 4 * 3 + 5 *

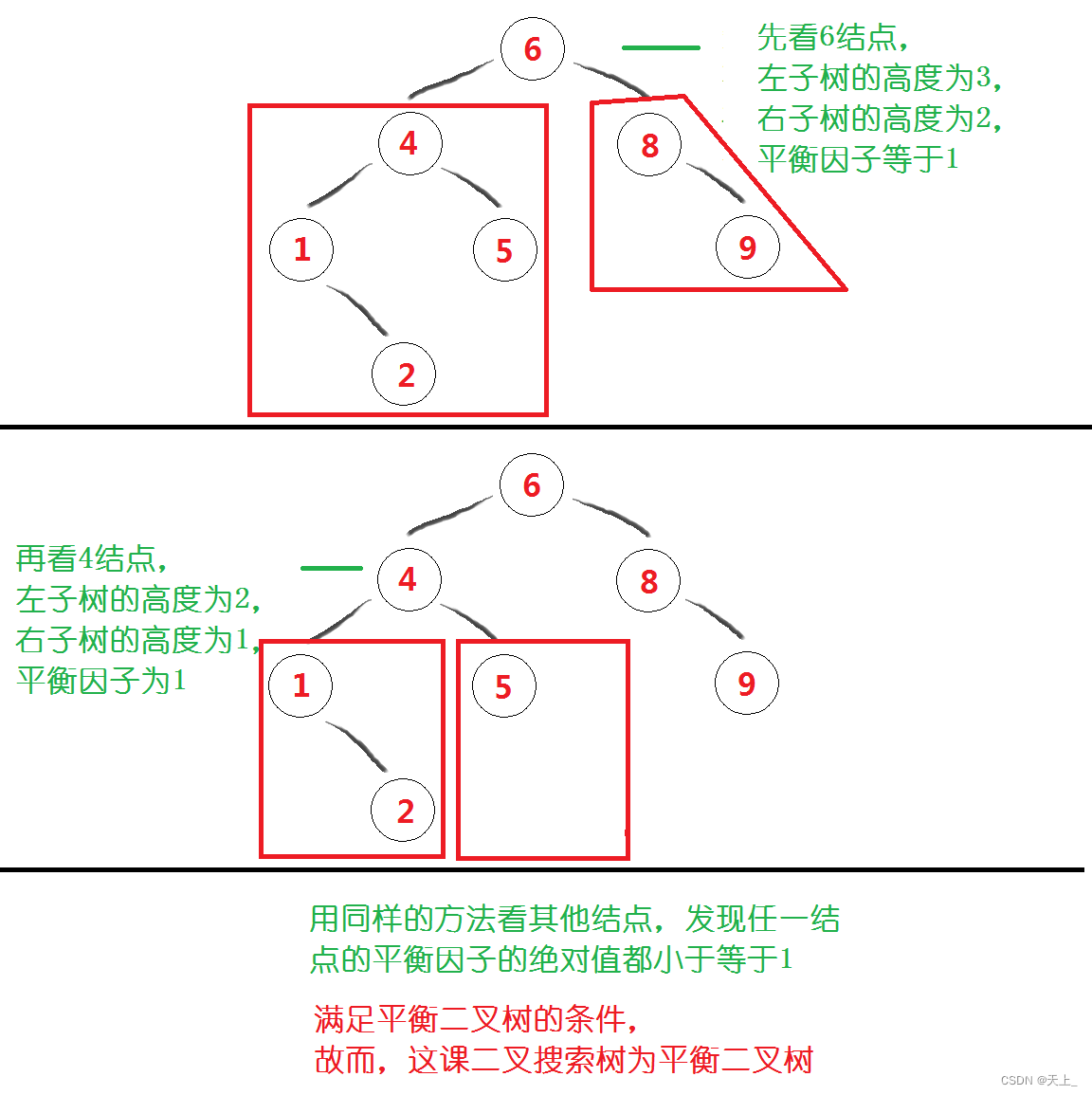
数据结构学习记录——什么是图（抽象数据类型定义、常见术语、邻接矩阵表示法、邻接表表示法）表示“多对多”的关系包含类型名称：图（Graph）数据对象集：G（V，E）由一个非空的有限顶点集合V和一个有限边集合E组成。操作集：对于任意图G属于Graph，以及v属于V，e属于E建立并返回空图将v插入G将e插入G从顶点v出发深度优先遍历图G从顶点v出发宽度优先遍历图G计算图G中顶点v到任意其他顶点的最短距离

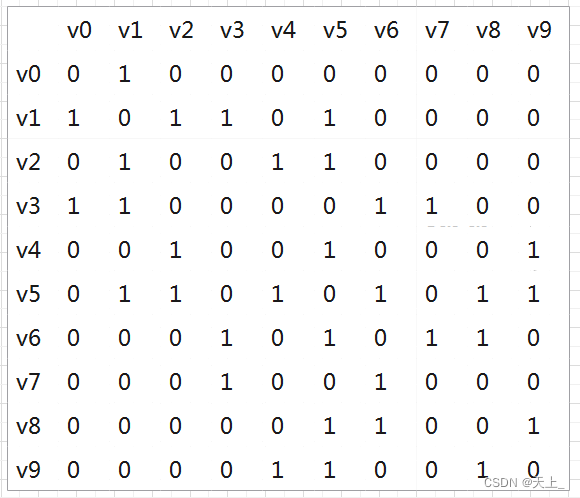
1.添加数据INSERT INTO 表名(字段名1,字段名2,...) VALUES(值1,值2,...)[,(值1,值2,...)];2.修改数据UPDATE 表名 SET 字段名1=值1,字段名2=值2,... [WHERE 条件];3.删除数据DELETE FROM 表名 [WHERE 条件];end学习自：黑马程序员——MySQL数据库课程。

二维数组表示图的邻接矩阵。它的大小是MaxVertexNum × MaxVertexNum，用于存储顶点之间边的权重或者存在的情况。（无权重且存在边用1表示，无权重且不存在边则用0表示；有权重且存在边用其权重表示，有权重且不存在边则用一个极大值表示。其中，DataType Data[MaxVertexNum]，可以用来存储与每个顶点相关的其他数据。例如：如果图表示一个社交网络，则可以存储每个顶点的

串行传输是指数据是一个比特一个比特依次发送的。因此在发送端和接收端之间，只需要一条数据传输线路即可。字节之间的时间间隔不是固定的，接收端仅在每个字节的起始处对字节内的比特实现同步。，也就是发送端将时钟同步信号编码到发送数据中一起传输，例如传统以太网所采用的就是曼彻斯特编码，这部分内容我们将在以后详细讨论。这里异步是指字节之间异步，也就是字节之间的时间间隔不固定，但字节中的每个比特仍然要同步，也就是

在之前的测试中，我们发现，如果数据量很大，在执行count操作时，是非常耗时的。MyISAM 引擎把一个表的总行数存在了磁盘上，因此执行 count(*) 的时候会直接返回这个数，效率很高；但是如果是带条件的count，MyISAM引起也慢。InnoDB 引擎就麻烦了，它执行 count(*) 的时候，需要把数据一行一行地从引擎里面读出来，然后累积计数。

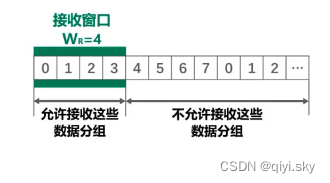
回退N帧协议的接收窗口尺寸只能等于一，因此接收方只能按序接收正确到达的数据分组；一个数据分组的误码就会导致其后续多个数据分组不能被接方按序接收而丢弃，尽管他们没有误码。这必然会造成发送方对这些数据分组的超时重传，显然这是对通信资源的极大浪费。为了进一步提高性能，可设法只重传出现误码的数据分组；因此，接收窗口的尺寸不应再等于1而应大于1；以便接收方先收下失序到达但无误码并且序号落在接收窗口内的那些数

根据曼彻斯特编码的特点，也就是每个码元在其中间时刻发生跳变，可以划分出所给信号中的各码元，至于正跳变表示1还是0，负跳变表示0还是1，没有具体规定，可以自行假设。调制后产生的信号是模拟信号，可以在模拟信号中传输，例如Wifi使用补码键控，直接序列扩频，正交频分复用等调制方法。编码后产生的信号仍为数字信号，可以在数字信道中传输，例如以太网使用曼彻斯特编码，4B/5B，8B/10B等。也就是说，信号是