问题:插值由其角节点已知的 3D 表面并使用颜色图对其进行着色

我想构建实验数据的 3D 表示来跟踪膜的变形。实验上,只有角节点是已知的。但是我想绘制整体结构的变形,这就是为什么我想对膜进行插值以实现它的漂亮颜色图。通过四处搜索,我几乎用以下代码接近它:

import numpy
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import matplotlib.pyplot as plt
from matplotlib import cm
from scipy.interpolate import griddata

x=numpy.array([0, 0, 1, 1])
y=numpy.array([0.5, 0.75, 1, 0.5])
z=numpy.array([0, 0.5, 1,0])

fig = plt.figure()
ax = Axes3D(fig)
verts = [zip(x, y, z)]
PC = Poly3DCollection(verts)
ax.add_collection3d(PC)

xi = numpy.linspace(x.min(),x.max(),20)
yi = numpy.linspace(y.min(),y.max(),20)
zi = griddata((x,y),z, (xi[None,:], yi[:,None]), method='linear')
xig, yig = numpy.meshgrid(xi, -yi)
ax.plot_surface(xig, yig, zi, rstride=1, cstride=1,  linewidth=0,cmap=plt.cm.jet,norm=plt.Normalize(vmax=abs(yi).max(), vmin=-abs(yi).max()))
plt.show()

并得到以下情节:

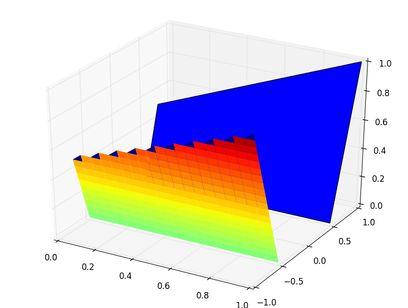
蓝色多边形是其角节点已知的表面,我想对其进行颜色映射。到目前为止,彩色映射表面是我最好的结果。然而,表面顶部附近的黑色多边形让我感到不安。我认为这可能是由于表面不适合网格,所以第四个角在这里是一个 Nan。

是否有避免这些黑色三角形的解决方法,或者更好的方法来对仅由其角节点已知的表面进行颜色映射?

编辑:这是使用以下命令在我的第一条评论中给出的三角测量解决方案的图

triang = tri.Triangulation(x, y)
ax.plot_trisurf(x, y, z, triangles=triang.triangles, cmap=cm.jet,norm=plt.Normalize(vmax=abs(yi).max(), vmin=-abs(yi).max()))

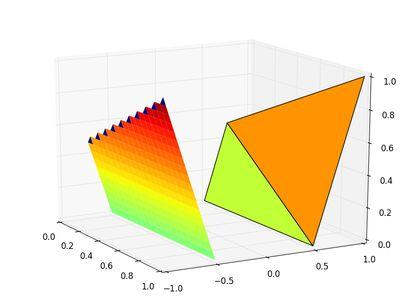
解答

问题归结为如何在 matplotlib 中对表面进行插值着色,即相当于 Matlab 的shading('interp')功能。简短的回答是:你不能。它本身不支持,所以最好的办法就是手工完成,这就是目前所提出的解决方案的目标。

几年前我沿着这条路走,当时我也对 Matlab 的shading('interp')感到沮丧:它通过简单地在每个四边形上插值 4 个角颜色来工作,这意味着颜色渐变的方向可以在相邻的四边形上不同。我想要的是每个色带恰好位于 z 轴上两个明确定义的值之间,相邻单元格之间没有视觉中断。

进行三角测量绝对是正确的想法。但不是简单地细化网格并希望达到相邻三角形的颜色在视觉上无法区分的点(没有达到首先出现伪影的点),我的方法是计算三角剖分上的轮廓带,然后将它们绘制成 3D .

当我第一次实现这个时,matplotlib 不支持三角剖分的轮廓。现在它通过_tri.TriContourGenerator完成。如果这也提供了提取的多边形顶点的 z 值,我们就完成了。不幸的是,它们在 Python 级别上无法访问,因此我们需要尝试通过比较create_filled_contours()和create_contours()的输出来重构它们,这在以下代码中完成:

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import matplotlib.pyplot as plt
from matplotlib import _tri, tri, cm

def contour_bands_3d(x, y, z, nbands=20):
    # obtain the contouring engine on a triangulation
    TRI = tri.Triangulation(x, y)
    C = _tri.TriContourGenerator(TRI.get_cpp_triangulation(), z)

    # define the band breaks
    brks = np.linspace(z.min(), z.max(), nbands+1)

    # the contour lines
    lines = [C.create_contour(b) for b in brks]

    # the contour bands
    bands = [C.create_filled_contour(brks[i], brks[i+1]) for i in xrange(nbands)]

    # compare the x, y vertices of each band with the x, y vertices of the upper
    # contour line; if matching, z = z1, otherwise z = z0 (see text for caveats)
    eps = 1e-6
    verts = []
    for i in xrange(nbands):
        b = bands[i][0]
        l = lines[i+1][0]
        z0, z1 = brks[i:i+2]
        zi = np.array([z1 if (np.abs(bb - l) < eps).all(1).any() else z0 for bb in b])
        verts.append(np.c_[b, zi[:,None]])
    return brks, verts

x = np.array([0, 0, 1, 1])
y = np.array([0.5, 0.75, 1, 0.5])
z = np.array([0, 0.5, 1,0])

fig = plt.figure()
ax = Axes3D(fig)
verts = [zip(x, y, z)]
PC = Poly3DCollection(verts)
ax.add_collection3d(PC)

# calculate the 3d contour bands
brks, verts = contour_bands_3d(x, -y, z)

cmap = cm.get_cmap('jet')
norm = plt.Normalize(vmax=abs(y).max(), vmin=-abs(y).max())

PC = Poly3DCollection(verts, cmap=cmap, norm=norm, edgecolors='none')
PC.set_array(brks[:-1])
ax.add_collection(PC)
ax.set_ylim((-1, 1))
plt.show()

这是结果:

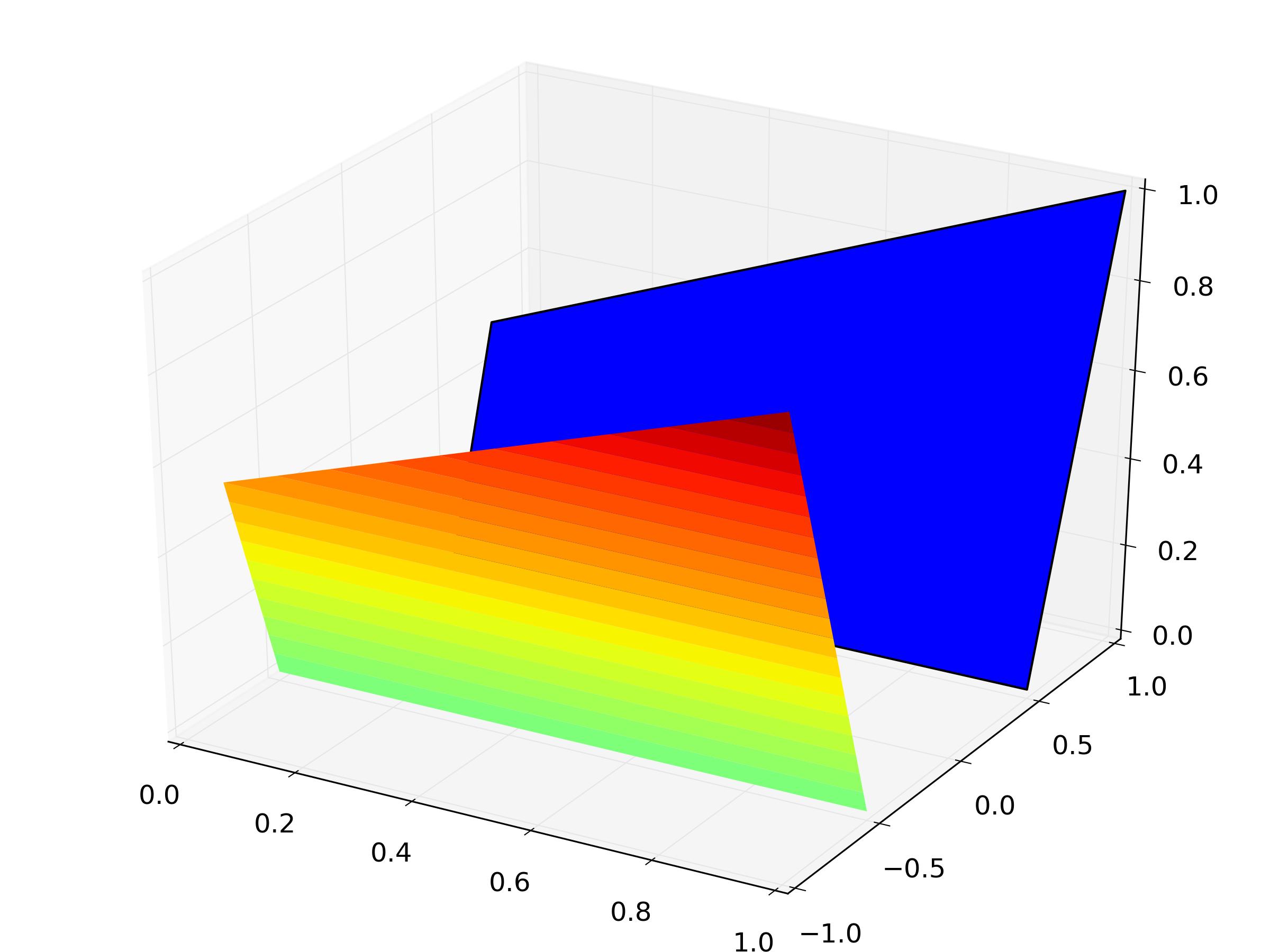
请注意,z 值的重建并不完全正确,因为我们还需要检查 x,y 顶点是否实际上是原始数据集的一部分,在这种情况下,必须采用其原始 z 值。但是,修改轮廓算法的 C++ 代码以跟踪 z 值会容易得多。这将是一个很小的变化,而试图涵盖 Python 中的所有情况简直就是一场噩梦。

关于效率,好吧,我们正在尝试在 Python 级别上完成显卡的工作,所以这将是可怕的。但这对所有mplot3d都是一样的。如果需要性能实现,我推荐BandedContourFilter()来自VTK。这工作得非常快,也可以在 Python 中使用。