回答问题

scipy.integrate.ode的(简要)文档说两种方法(dopri5和dop853)具有步长控制和密集输出。查看示例和代码本身,我只能看到一种从集成器获取输出的非常简单的方法。即,看起来您只是将积分器向前推进某个固定的 dt,获取当时的函数值,然后重复。

我的问题有相当多变的时间尺度,所以我想在需要评估的任何时间步骤获取值以达到所需的容差。也就是说,在早期,事情正在缓慢变化,因此输出时间步长可能很大。但随着事情变得有趣,输出时间步长必须更小。我实际上并不想要等间隔的密集输出,我只想要自适应函数使用的时间步长。

编辑:密集输出

一个相关的概念(几乎相反)是“密集输出”,其中所采取的步数与步进器一样大,但函数的值被插值(通常精度与步进器的精度相当)到任何你要。 fortran底层scipy.integrate.ode显然可以做到这一点,但是ode没有接口。另一方面,odeint是基于不同的代码,并且显然会进行密集输出。 (您可以在每次调用右侧时输出以查看何时发生,并查看它与输出时间无关。)

所以我仍然可以利用适应性,只要我可以提前决定我想要的输出时间步长。不幸的是,对于我最喜欢的系统,我什至不知道作为时间函数的大致时间尺度是什么,直到我运行集成。因此,我必须将采取积分器步骤的想法与密集输出的概念结合起来。

编辑2:再次密集输出

显然,scipy 1.0.0 通过一个新接口引入了对密集输出的支持。特别是,他们建议从scipy.integrate.odeint移到scipy.integrate.solve_ivp,这是一个关键字dense_output。如果设置为True,则返回的对象具有属性sol,您可以使用时间数组调用该属性,然后返回这些时间的集成函数值。这仍然不能解决这个问题的问题,但在许多情况下它很有用。

Answers

由于SciPy 0.13.0,

现在可以通过solout回调函数访问dopri系列 ODE 求解器的中间结果。

import numpy as np
from scipy.integrate import ode
import matplotlib.pyplot as plt


def logistic(t, y, r):
    return r * y * (1.0 - y)

r = .01
t0 = 0
y0 = 1e-5
t1 = 5000.0

backend = 'dopri5'
# backend = 'dop853'
solver = ode(logistic).set_integrator(backend)

sol = []
def solout(t, y):
    sol.append([t, *y])
solver.set_solout(solout)
solver.set_initial_value(y0, t0).set_f_params(r)
solver.integrate(t1)

sol = np.array(sol)

plt.plot(sol[:,0], sol[:,1], 'b.-')
plt.show()

结果: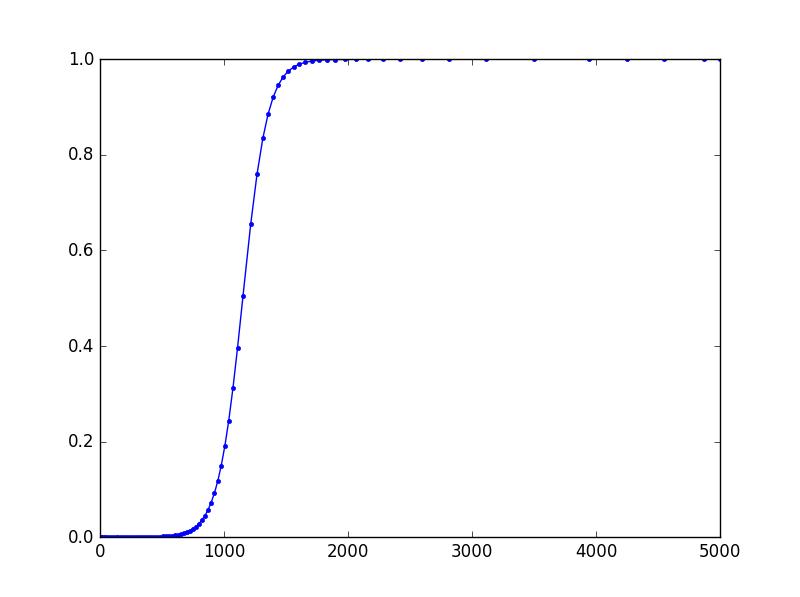

结果似乎与 Tim D 的略有不同,尽管他们都使用相同的后端。我怀疑这与dopri5的 FSAL 属性有关。在 Tim 的方法中,我认为第七阶段的结果 k7 被丢弃,因此重新计算 k1。

注意:如果您在设置初始值](https://stackoverflow.com/questions/26738676/does-scipy-integrate-ode-set-solout-work)之后设置它,则存在已知的[错误 set_solout 不起作用。它从SciPy 0.17.0开始修复。