sklearn简介--sklearn中回归决策树的实现_示例演示1

1.回归树简介

几乎所有像两个豌豆一样的参数都是分类。回归树函数的参数如下:

class sklearn.tree.DecisionTreeRegressor (criterionu003d'mse', splitteru003d'best', max_depthu003dNone,min_samples_splitu003d2, min_samples_leafu003d1, min_weight_fraction_leafu003d 0.0, max_featuresu003dNone,random_stateu003dNone, max_leaf_nodesu003dNone, min_impurity_decreaseu003d0.0, min_impurity_splitu003dNone, presortu003dFalse)

2.重要参数、属性和接口

准则:回归树是衡量分支质量的指标。支持三种类型的标准:

• 输入“mse”使用均方误差(mse),父节点与叶节点的均方误差之差将作为

该方法通过使用叶节点的平均值来最小化 L2 损失。

• 输入“friedman_mse”使用费尔德曼均方误差,它使用弗里德曼改进的均方误差来解决潜在分支问题。

• 输入“MAE”使用绝对平均误差MAE(mean absolute error),它使用叶子节点的中值来最小化L1损失。

最重要的属性是feature_importances_,用来查看属性的重要性。

最重要的接口是:应用、拟合、预测和评分。

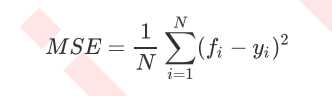
其中N是样本个数,i是每个数据样本,fifi是模型回归的值,yi是样本点i的实际值标签。 MSE实际上是样本真实数据和回归结果之间的差异。在回归中,我们追求的是 MSE 越小越好。因为 MSE 越小,预测值与实际值的差异越小,预测就越准确。

但是,回归树接口分数返回 r 平方,而不是 MSE。 R 平方定义如下:

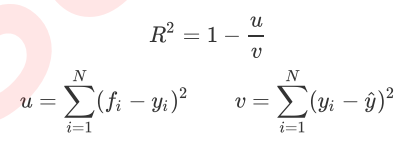
其中u是残差平方和(MSE*N),v是平方和,N是样本数,i是每个数据样本,fifi是模型回归的值,yi是实际样本点 i 的值标签。 y 上限是实际值标签的平均数量。 R平方可以是正的也可以是负的(如果模型的残差平方和远大于模型的总平方和,模型很糟糕,R平方就会为负),并且均方误差总是要乐观。

值得一提的是,虽然均方误差始终为正,但在sklearn中以均方误差作为评价标准时,是计算负均方误差(neg_mean_squared_error)。这是因为sklearn在计算模型评价指标时,会考虑指标本身的性质。均方误差本身就是一个误差,所以被sklearn划分为模型的一个loss。因此,在sklearn中,表示为负数。真正的均方误差 MSE 实际上是 NEG_ mean_ squared_ Error 去掉带减号的数字。

3. sklearn中的回归树

from sklearn.datasets import load_boston #导入波士顿房价数据集

from sklearn.model_selection import cross_val_score #导入交叉验证

from sklearn.tree import DecisionTreeRegressor #导入回归树

boston u003d load_boston() #将boston数据集赋值给变量boston

regressor u003d DecisionTreeRegressor(random_stateu003d0) #生成回归树

cross\val\score(回归,boston.data,boston.target,cvu003d10,

score u003d "neg\mean\squared\error") #交叉验证_ val_分数的使用

这是一个简单的调用。在和boston打交道的时候,我们可以利用numpy的知识来简单的查看数据。

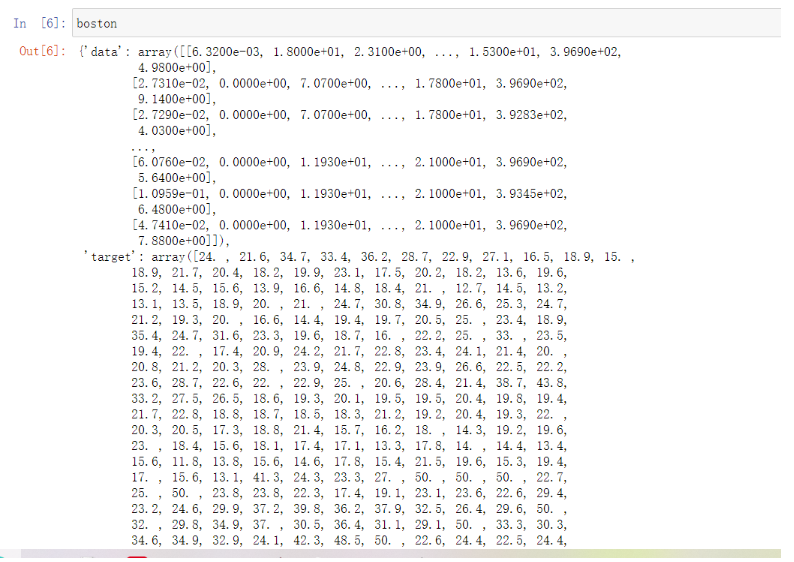
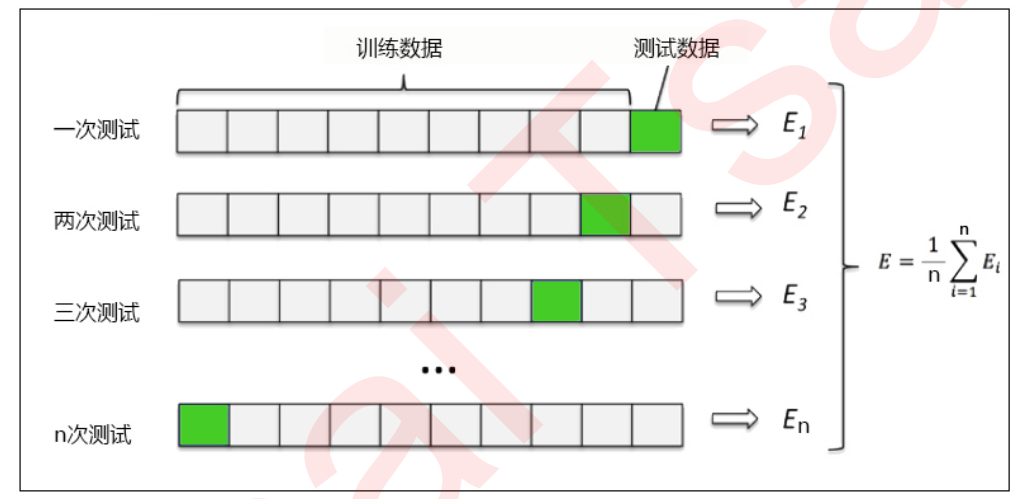
可以看到输入boston返回的数据是字典的形式。我们也可以输入 boston Data 来查看特征和 boston Target 和 target 值。交叉验证是一种用于观察模型稳定性的方法。我们将数据分成N份,一份作为测试集,另外n-1份作为训练集,多次计算模型的准确率来评估模型的平均准确率。训练集和测试集的划分会干扰模型的结果,所以交叉验证n次的结果取平均值是更好的衡量模型效果的指标。

4.示例:一维回归的图像渲染

4.1 导入所需库

import numpy as np #用于快速处理数据

从 sklearn.tree 导入 DecisionTreeRegressor

import matplotlib.pyplot as plt #用来画图

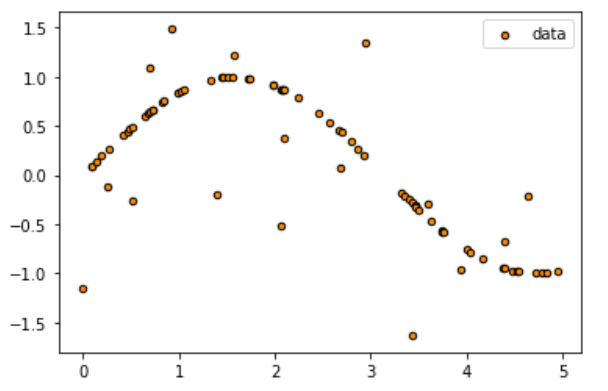
4.2 创建带噪声的正弦曲线

这一步,我们的基本思路是创建一组分布在0~5的横坐标轴的随机值(x),然后将这组值放入sin函数中生成纵坐标的值(y),然后加入噪声玩具。在整个过程中,我们将使用 numpy 库为我们生成这个正弦。

rng u003d np.random.RandomState(1)

X u003d np.sort(5 * rng.rand(80,1),axisu003d0)#axisu003d0表示按行计算,axisu003d1表示按列计算。

#rng.rand(80,1) 生成80个值为0-1的点,然后乘以5将点的值放大到0-5。

#然后使用排序函数将行从大到小排序。

y u003d np.sin(X).ravel()#np.sin(x) 是二维数据。使用 travel() 将数据变为一维数据,用于正常输入到回归树中。

y[::5] +u003d 3 * (0.5 - rng.rand(16)) #80个数据点,每5个点取一个值,加上噪声。

#Y [start point: end point: step size] y[::5] 表示从开始到结束,步长为5。

#80分,共16分,0.5 - RNG rand(16)的范围是 - 0.5 ~ 0.5。

4.3 实例化和训练模型

regr_1 u003d DecisionTreeRegressor(max_depthu003d2) #树的深度为2

regr_2 u003d DecisionTreeRegressor(max_depthu003d5) #树的深度为5

regr_1.fit(X, y) #进行训练

regr_2.fit(X, y)

4.4 测试集导入模型及预测结果

X_test u003d np.arange(0.0, 5.0, 0.01)[:, np.newaxis]

#np。 Array(起点、终点、步长)函数生成有序数组

y_1 u003d regr_1.predict(X_test)

y_2 u003d regr_2.predict(X_test)

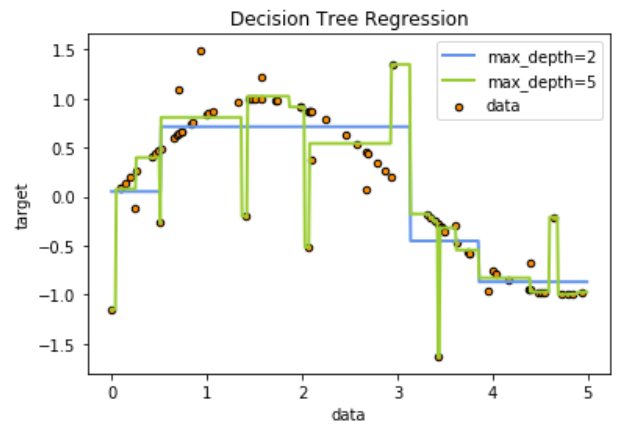
4.5 绘图图片

plt.figure()

plt.scatter(X, y, su003d20, edgecoloru003d"black",cu003d"darkorange", labelu003d"data")

plt.plot(X_test, y_1, coloru003d"cornflowerblue",labelu003d"max_depthu003d2", linewidthu003d2)

plt.plot(X_test, y_2, coloru003d"yellowgreen", labelu003d"max_depthu003d5", linewidthu003d2)

plt.xlabel("数据")

plt.ylabel("目标")

plt.title("决策树回归")

plt.legend()

plt.show()