超参数优化方法:网格搜索、随机搜索、贝叶斯优化(BO)等算法。

参考资料:三种超参数优化方法详解,以及代码实现

实验基础代码

将 numpy 导入为 np

将熊猫导入为 pd

从 lightgbm.sklearn 导入 LGBMRegressor

从 sklearn.metrics 导入均值_squared_error

进口警告

警告.filterwarnings('忽略')

从 sklearn.datasets 导入负载_diabetes

从 sklearn.model_selection 导入 KFold,cross_val_score

从 sklearn.model_selection 导入火车_test_split

导入时间

导入我们

导入 psutil

在 sklearn Datasets 的糖尿病数据集中演示并比较不同的算法来加载它。

糖尿病 u003d 负载_糖尿病()

数据 u003d 糖尿病数据

目标 u003d 糖尿病.目标

n u003d data.shape[0]

随机_state u003d 42

时间占用s

开始 u003d timeit.default_timer()

内存使用量mb

info_start u003d psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024

训练_数据、测试_数据、训练\目标、测试\目标 u003d 训练\测试\拆分(数据、目标、

测试_sizeu003d0.20,随机播放u003d真,

随机_stateu003d随机_state)

数量_folds u003d 2

kf u003d KFold(n_splitsu003dnum_folds, random_stateu003drandom_state, shuffleu003dTrue)

模型 u003d LGBMRegressor(随机_stateu003d随机_state)

score u003d -cross_val_score(模型,train_data,train\targets,cvu003dof,scoringu003d"neg\mean\squared_error",n_jobsu003d-1).mean()

print('分数:',分数)

结束 u003d timeit.default_timer()

info_end u003d psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024

print('这个程序占用内存' + str(info_end - info_start) + 'mB')

print('运行时间:%.5fs' % (end - start))

实验结果如下:

最小二乘误差:3897.5550693355276

此程序占用 0.5mB 内存

运行时间:1.48060s

出于比较的目的,我们将优化只调整以下三个参数的模型:

n_estimators:从 100 到 2000

最大_深度:2 到 20

learning_rate:从 10e-5 到 1

1、网格搜索

网格搜索可能是最简单和最广泛使用的超参数搜索算法。它通过查找搜索范围内的所有点来确定最佳值。如果使用较大的搜索范围和较小的步长,则网格搜索很有可能找到全局最优值。但是,这种搜索方案会消耗大量的计算资源和时间,尤其是在有很多超参数需要调优的情况下。

因此,在实际应用过程中,网格搜索方法一般采用较宽的搜索范围和较大的步长来寻找全局最优值的可能位置;然后缩小搜索范围和步长以找到更准确的最优值。这种运算方案可以减少所需的时间和计算量,但由于目标函数一般是非凸的,因此很可能错过全局最优值。

网格搜索元素对应于sklearnGridSearchCV模块中的元素:sklearn model_ selection。 GridSearchCV

(估计器,参数_grid,,评分u003d无,n_jobsu003d无,iidu003d'deprecated',refitu003dTrue,cvu003dNone,详细u003d0,pre_dispatchu003d'2n_jobs',错误_scoreu003d南,返回_train_scoreu003dFalse)。详见博客。

1.1 GridSearch算法代码

从 sklearn.model_selection 导入 GridSearchCV

时间占用s

开始 u003d timeit.default_timer()

内存使用量mb

info_start u003d psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024

参数_grid u003d {'learning_rate': np.logspace(-3, -1, 3),

'max_depth': np.linspace(5, 12, 8, dtypeu003dint),

'n_estimators': np.linspace(800, 1200, 5, dtypeu003dint),

'随机_state':[随机_state]}

gs u003d GridSearchCV(模型,参数_grid,评分u003d'neg_mean_squared_error',

n_jobsu003d-1,cvu003dkf,详细u003d假)

gs.fit(训练_数据,训练_targets)

gs_test_score u003d mean_squared_error(test_targets, gs.predict(test_data))

结束 u003d timeit.default_timer()

info_end u003d psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024

print('这个程序占用内存' + str(info_end - info_start) + 'mB')

print('运行时间:%.5fs' % (end - start))

print("最佳 MSE {:.3f} 参数 {}".format(-gs.best_score_, gs.best_params_))

实验结果:

该程序占用12.79296875mB内存

运行时间:6.35033s

最佳 MSE 3696.133 参数 {'learning_rate': 0.01, 'max_depth': 5, 'n_estimators': 800, 'random_state': 42}

1.2 视觉解读

导入 matplotlib.pyplot 作为 plt

gs_results_df u003d pd.DataFrame(np.transpose([-gs.cv_results_['mean_test_score'],

gs.cv_results_['param_learning_rate'].data,

gs.cv_results_['param_max_depth'].data,

gs.cv_results_['param_n_estimators'].data]),

columnsu003d['score', 'learning_rate', 'max_depth',

'n_estimators'])

gs_results_df.plot(subplotsu003dTrue, figsizeu003d(10, 10))

plt.show()

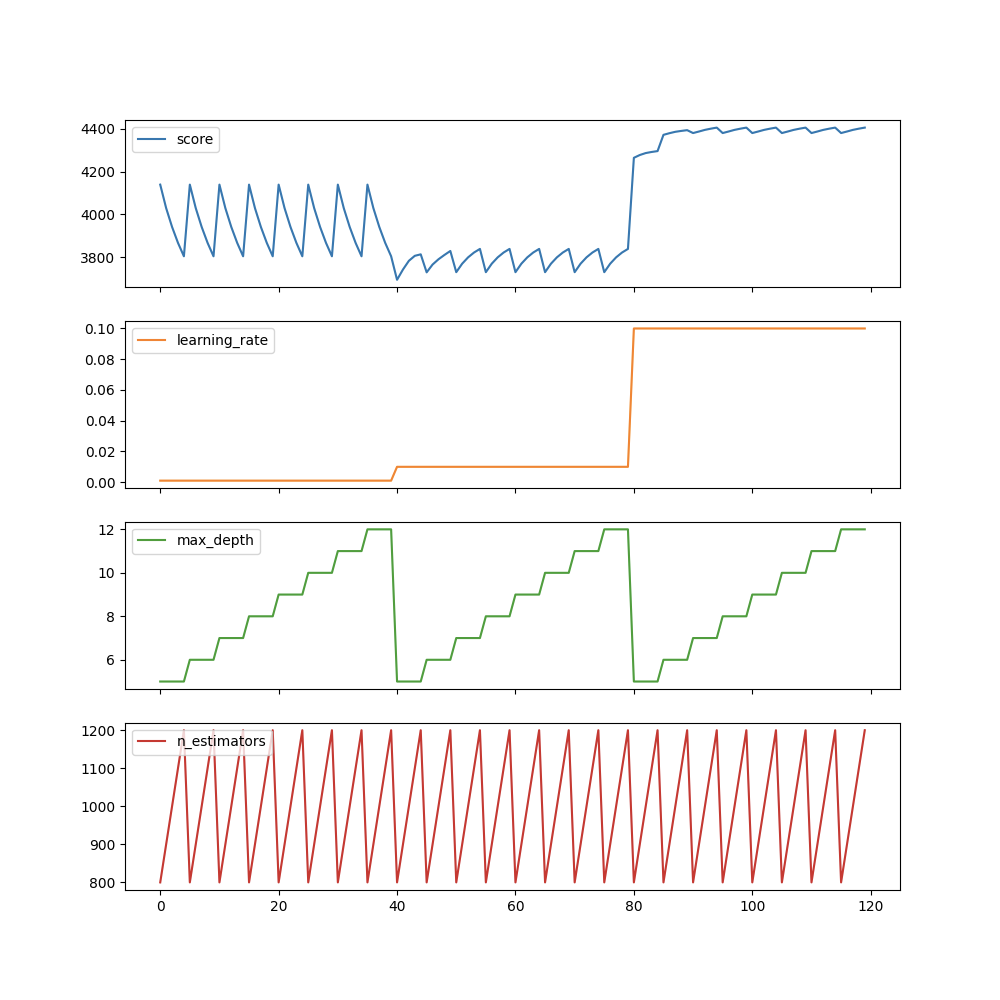
例如,我们可以看到,max_depth 是最不重要的参数,它不会显着影响分数。但是,我们在搜索 max_ 八个不同的深度值,在其他参数上搜索任何固定值。显然是浪费时间和资源。

2、随机搜索

https://www.cnblogs.com/cgmcoding/p/13634531.html

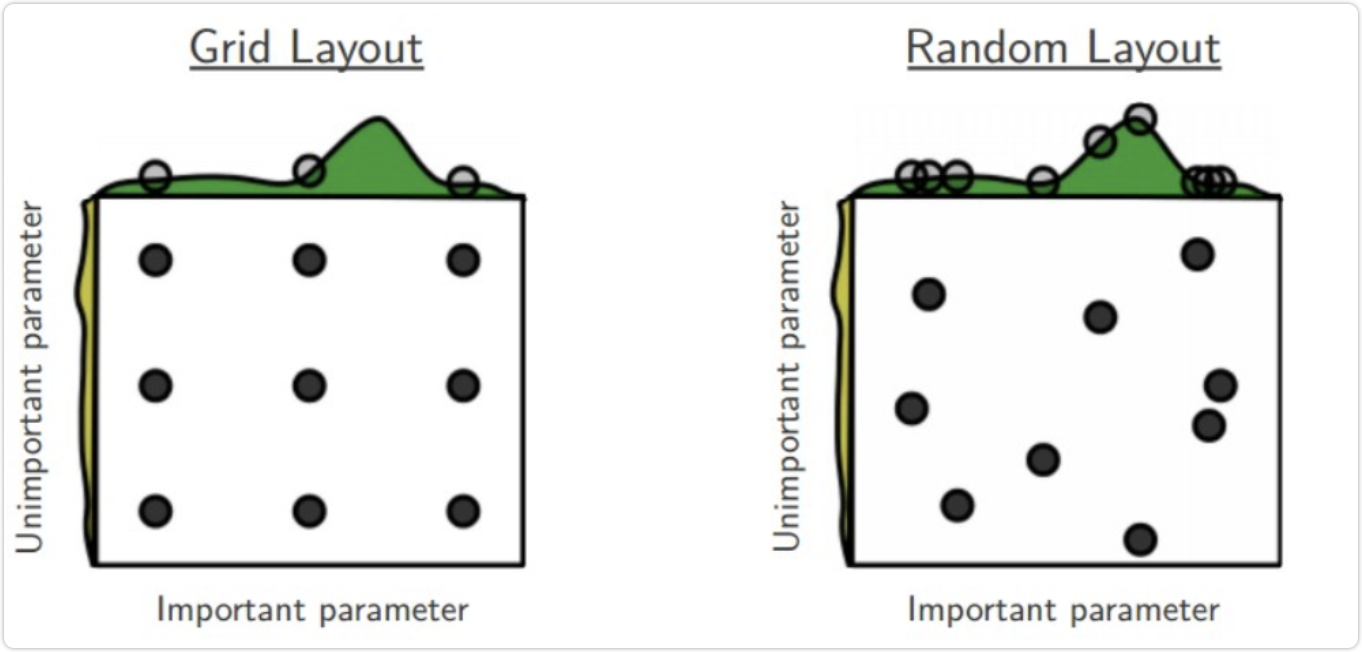
随机搜索的思想类似于网络搜索,只是不再测试上下界之间的所有值,而是在搜索范围内随机选取样本点。他的理论基础是,如果样本点集足够大,可以通过随机抽样大致找到全局最优值或近似值。随机搜索通常比网络搜索快。在搜索超参数时,如果超参数的数量很少(三个或四个或更少),我们可以使用网格搜索,一种穷举搜索方法。但是,当超参数的数量很大时,我们仍然使用网格搜索,搜索时间会成倍增加。

因此,有人提出了一种随机搜索的方法,在超参数空间中随机搜索数百个点,其中可能有比较小的值。该方法比上述稀疏网格方法速度快,实验表明随机搜索方法比稀疏网格方法略好。 RandomizedSearchCV 使用类似于 GridSearchCV 类的方法,但它不是尝试所有可能的组合,而是选择每个超参数的随机值的特定数量的随机组合。这种方法有两个优点:

如果您运行随机搜索,例如 1000 次,它将探索每个超参数的 1000 个不同值(而不是每个超参数的几个值,如网格搜索)

您可以通过设置搜索次数轻松控制超参数搜索的计算量。

随机化searchcv的使用方法其实和GridSearchCV是一样的,只不过它通过在参数空间中随机采样来代替GridSearchCV的网格搜索参数。对于具有连续变量的参数,随机化searchcv会将它们采样为分布,这对于网格搜索是不可能的,其搜索能力取决于设置的n_iter参数,给出相同的代码。

在 sklearn 模型_ 选择中随机搜索 sklearn。随机搜索CV

(估计器,param_distributions,*,n_iter u003d 10,score u003d None,n_jobs u003d None,iid u003d 'deprecated',refine u003d true,cv u003d None,verbose u003d 0,pre_dispatch u003d '2 * n_jobs', random_state u003d None, error_score u003d nan, _return_train_score u003d False) 参数与GridSearchCV大致相同,但多了一个n_ ITER是个数迭代轮次。

从 sklearn.model_selection 导入 RandomizedSearchCV

从 scipy.stats 导入 randint

参数_grid_rand u003d {'learning_rate': np.logspace(-5, 0, 100),

'max_depth': randint(2, 20),

'n_estimators': randint(100, 2000),

'随机_state':[随机_state]}

时间占用s

开始 u003d timeit.default_timer()

内存使用量mb

info_start u003d psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024

rs u003d RandomizedSearchCV(模型,参数_grid_rand,n_iteru003d50,评分u003d'neg\mean\squared\error',

n_jobsu003d-1, cvu003dkf, verboseu003dFalse, random_stateu003drandom_state)

rs.fit(火车_数据,火车_targets)

rs_test_score u003d mean_squared_error(test_targets, rs.predict(test_data))

结束 u003d timeit.default_timer()

info_end u003d psutil.Process(os.getpid()).memory_info().rss / 1024 / 1024

print('这个程序占用内存' + str(info_end - info_start) + 'mB')

print('运行时间:%.5fs' % (end - start))

print("最佳 MSE {:.3f} 参数 {}".format(-rs.best_score_, rs.best_params_))

此程序占用 17.90625mB 内存

运行时间:3.85010s

最佳 MSE 3516.383 参数 {'learning_rate': 0.0047508101621027985, 'max_depth': 19, 'n_estimators': 829, 'random_state': 42}

可以看出运行50轮时效果比GridSearchCV好,时间也更短。

3、贝叶斯优化(BO)

网格搜索速度慢,但在搜索整个搜索空间时效果很好,而随机搜索速度快,但可能会错过搜索空间中的重要点。幸运的是,还有第三种选择:贝叶斯优化。在本文中,我们将重点介绍一种称为 Python 模块化 hyperopt 的贝叶斯优化实现。贝叶斯优化算法用于寻找最优和最大参数。它采用了与网格搜索和随机搜索完全不同的方法。在测试一个新点时,网格搜索和随机搜索都会忽略前一个点的信息,而贝叶斯优化算法则充分利用了前一个点的信息。贝叶斯优化算法学习目标函数的形状并找到将目标函数提高到全局最优值的参数。

具体来说,学习目标函数的方法是根据先验分布假设一个搜索函数;然后,每使用一个新的采样点来测试目标函数,这个信息就被用来更新目标函数的先验分布;最后,算法测试后验分布给出的全局最大值可能出现的点。对于贝叶斯优化算法,需要注意的一点是,一旦找到一个局部最优值,就会在该区域内不断采样,因此很容易陷入局部最优值。为了弥补这个缺点,贝叶斯算法会在探索和利用之间找到一个平衡点。探索是在未被采样的区域中获取采样点,而利用会根据后验分布在最可能的全局最大区域中进行采样。

我们将使用[hyperopt library](http://hyperopt.github.io/hyperopt/#documentation)来处理这个算法。它是最流行的超参数优化库之一。有关详细信息,请参阅博客。

(1)TPE算法:

算法u003dtpe.suggest

TPE 是 Hyperopt 的默认算法。它使用贝叶斯方法进行优化。在每一步,它都试图建立函数的概率模型,并为下一步选择最有希望的参数。这种算法的工作原理如下:

1.生成随机初始点x

2.计算F(x)

3.尝试利用测试历史建立条件概率模型P(F|x)

4.根据P(F|x)选择xi最有可能导致更好的F(xi)

5.计算F(xi)的实际值

6.重复步骤3-5,直到满足其中一个停止条件,如I > max_evals

从 hyperopt 导入 fmin、tpe、hp、anneal、Trials

def gb_mse_cv(params, random_stateu003drandom_state, cvu003dkf, Xu003dtrain_data, yu003dtrain_targets):

函数在“param”中获取一组可变参数

参数 u003d {'n_estimators': in(params['n_estimators']),

'max_depth':在(参数['max_depth']),

'learning_rate': 参数['learning_rate']}

我们使用这个参数来创建一个新的 LGBM Regressor

模型 u003d LGBMRegressor(随机_stateu003d随机_state,**参数)

然后进行与之前相同折叠的交叉验证

score u003d -cross_val_score(模型, X, y, cvu003dcv, scoreu003d"neg\mean\squared\error", n_jobsu003d-1).mean()

返回分数

状态空间,最小化函数params的取值范围

空间u003d{'n_estimators': hp.quuniform('n_estimators', 100, 2000, 1),

'max_depth' : hp.quniform('max_depth', 2, 20, 1),

'学习_rate': hp.loguniform('learning_rate', -5, 0)

}

试验会记录一些信息

试验 u003d 试验()

#时间占用

开始u003dtimeit.default_timer()

#内存使用量mb

info_start u003d psutil.Process(os.getpid()).memory_info().rss/1024/1024

bestu003dfmin(fnu003dgb_mse_cv, # 优化函数

空间u003d空间,

algou003dtpe.suggest, #优化算法,hyperotp会自动选择它的参数

max_evalsu003d50, # 最大迭代次数

试验u003d试验,# 记录

Estateu003dnp.random.RandomState(random_state) # 修复随机状态以获得可重复性

)

计算测试集的分数

模型 u003d LGBMRegressor(random_stateu003drandom_state, n_estimatorsu003dint(best['n_estimators']),

max_depthu003din(best['max_depth']),learning_rateu003dbest['learning_rate'])

model.fit(训练_数据,训练_targets)

tpe_test_scoreu003dmean_squared_error(test_targets, model.predict(test_data))

结束u003dtimeit.default_timer()

info_end u003d psutil.Process(os.getpid()).memory_info().rss/1024/1024

print('本程序占用内存'+str(info_end-info_start)+'mB')

print('运行时间:%.5fs'%(end-start))

print("最佳 MSE {:.3f} 参数 {}".format( gb_mse_cv(best), best))

实验结果:

该程序占用2.5859375mB内存

运行时间:52.73683s

最佳 MSE 3186.791 参数 {'learning_rate': 0.026975706032324936, 'max_depth': 20.0, 'n_estimators': 168.0}

4、结论

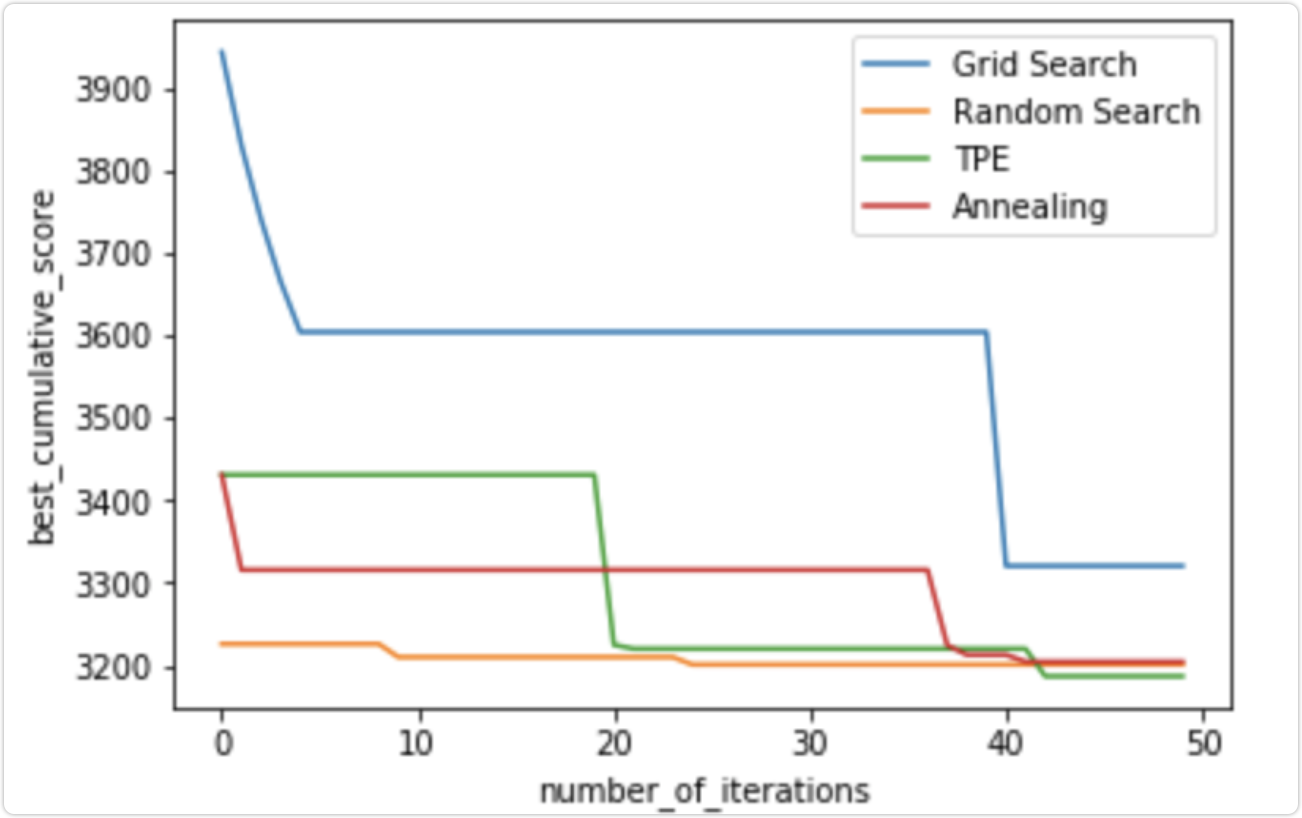
我们可以看到,即使在接下来的步骤中,TPE 和退火算法实际上也会随着时间的推移改善搜索结果,而随机搜索在开始时随机找到了一个很好的解决方案,然后只是稍微改善了结果。目前 TPE 和 RandomizedSearch 结果之间的差异很小,但是 hyperopt 在一些具有更多样化超参数范围的实际应用中可以显着提高时间/分数