深度学习系列 | 常用激活函数
摘要:激活函数是神经网络实现非线性的关键组件,通过将线性计算结果转换为非线性输出,使网络能够处理复杂模式。常见激活函数包括:Sigmoid(输出0-1,适合概率)、Tanh(输出-1-1,对称性强)、ReLU(简单高效但易导致神经元"死亡")和LeakyReLU(改进ReLU,避免完全失效)。虽然激活函数解决了线性模型的局限性,但也存在梯度消失、神经元死亡等问题。代码示例展示了
·
一、一句话总结
激活函数就像给神经网络装了 “非线性开关”,让它能处理复杂的曲线关系或分类问题,而不只是简单的直线划分。
二、生活案例类比
激活函数就像 “老师批改作业的方式”:
- 线性计算是 “统计错题数”(原始分数);
- Sigmoid 像 “按比例给分”:无论错多少题,最终成绩只在 0-100 分之间(避免负分或超满分);
- Tanh 像 “正负评分”:做得好加分(+1 到 + 100),做得差扣分(-1 到 - 100),更公平;
- ReLU 像 “只看对题”:对的题给分,错的题直接 0 分(简单但可能忽略进步空间);
- Leaky ReLU 像 “错题为负分但扣分少”:错的题扣少量分(比如错 1 题扣 0.01 分),既指出错误,又不让学生彻底放弃(避免神经元死亡)。
三、拆解知识步骤
1. 由来背景
早期神经网络只有 “线性计算”(比如y=wx+b),就像只用直尺画直线 —— 无论叠多少层,结果还是直线,无法拟合曲线(比如 “房价与面积的非线性关系”“图像中复杂的边缘轮廓”)。
为了让网络能处理 “非线性问题”,科学家引入 “激活函数”:通过对线性结果做非线性变换(把直线 “掰弯”),让多层网络叠加后能拟合复杂的曲线或分类边界。
2. 目标及解决的问题
核心目标:给神经网络注入 “非线性能力”,让它能处理线性模型搞不定的复杂任务。
解决的痛点:
- 突破线性局限:线性模型无法分开 “太极图”“异或问题” 等非线性数据,激活函数通过 “掰弯” 边界实现准确划分;
- 控制信号范围:线性计算可能让输出变得极大或极小(如输入 100→输出 10000),激活函数通过限制范围(0-1、-1-1 等)避免信号爆炸;
- 提升学习效率:ReLU 及变种计算简单(无需指数运算),让网络训练更快。
3. 实现逻辑
所有激活函数都是神经网络 “神经元” 的 “最后一步操作”,流程统一:
- 第一步:神经元先做线性计算(z=wx+b 汇总输入特征的加权和);
- 第二步:将z传入激活函数,得到非线性输出(如
“Sigmoid 输出”);
- 第三步:这个非线性输出作为下一层的输入,层层传递后,网络整体具备拟合非线性关系的能力(比如从 “像素值” 到 “这是猫” 的复杂映射)。
4. 局限性
|
函数 |
局限性 |
图示 |
|
Sigmoid |
输入极端值(x太大或太小)时,输出接近 1 或 0,梯度几乎为 0→导致 “梯度消失”(网络学不动)。 |
|
|
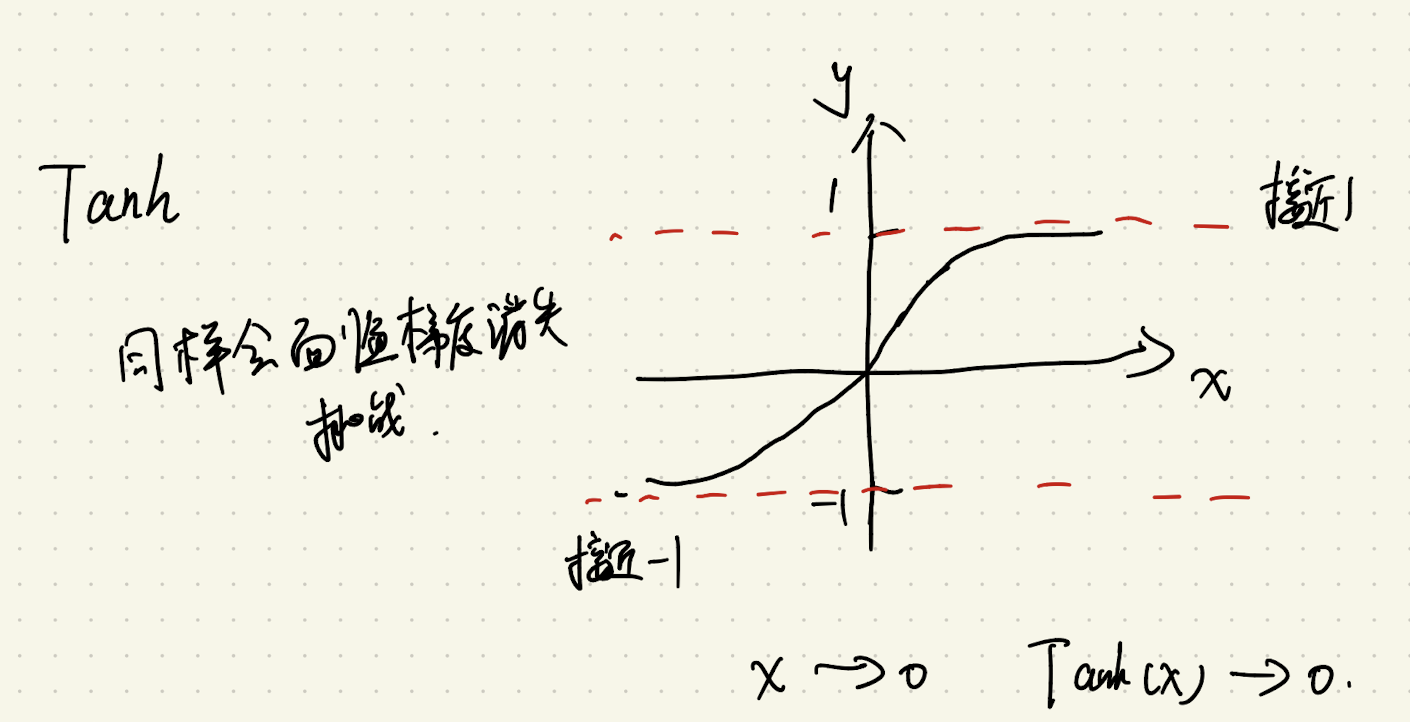
Tanh |
虽比 Sigmoid 对称,但输入极端值时梯度仍接近 0→同样易梯度消失。 |
|
|
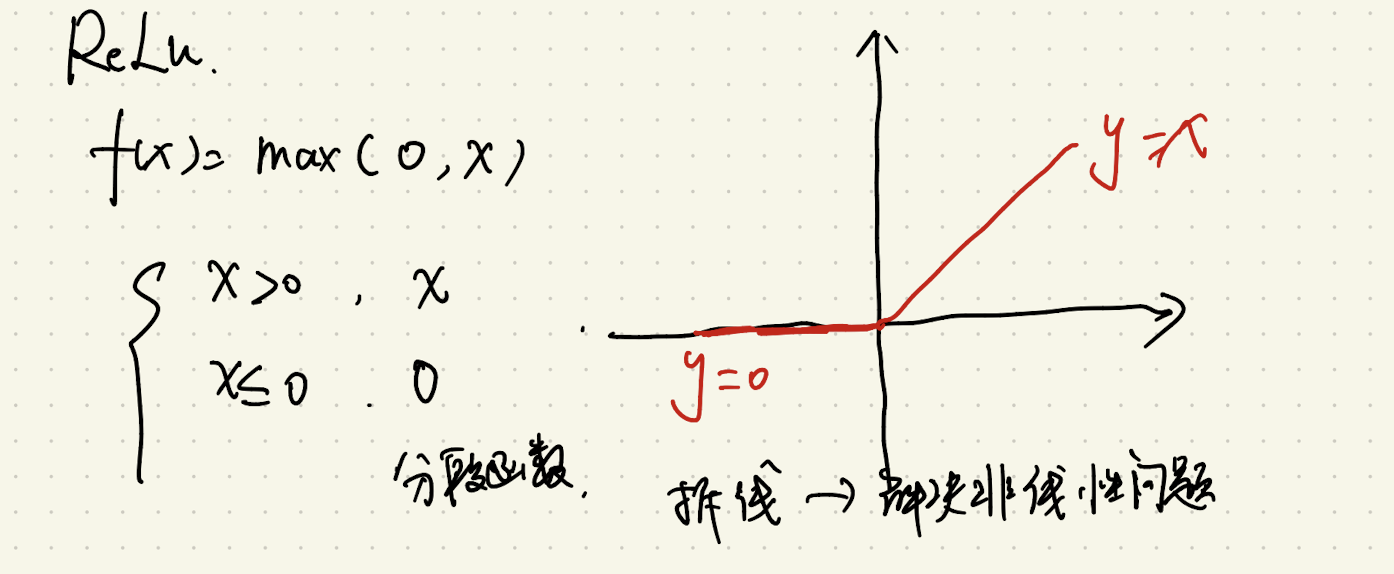
ReLU |
输入为负数时输出 0,梯度也为 0→导致 “死亡神经元”(永久不更新,像阀门锈死)。 |
|
|
Leaky ReLU |
需要人工设定 |
|
五、代码实现
import numpy as np
import matplotlib.pyplot as plt
# 设置matplotlib字体,解决中文显示问题(适用于macOS)
plt.rcParams["font.family"] = ["Arial Unicode MS", "SimHei"]
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 1. 实现激活函数
def sigmoid(x):
"""Sigmoid激活函数:将输入映射到(0, 1)"""
return 1 / (1 + np.exp(-x))
def tanh(x):
"""Tanh激活函数:将输入映射到(-1, 1)"""
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
def relu(x):
"""ReLU激活函数:x>0时输出x,否则输出0"""
return np.maximum(0, x)
def leaky_relu(x, alpha=0.01):
"""Leaky ReLU激活函数:x>0时输出x,否则输出alpha*x(解决死亡ReLU问题)"""
return np.where(x > 0, x, alpha * x)
# 2. 生成输入数据(范围从-10到10,足够展示函数特性)
x = np.linspace(-10, 10, 1000) # 生成1000个均匀分布的点
# 3. 计算各激活函数的输出
y_sigmoid = sigmoid(x)
y_tanh = tanh(x)
y_relu = relu(x)
y_leaky_relu = leaky_relu(x)
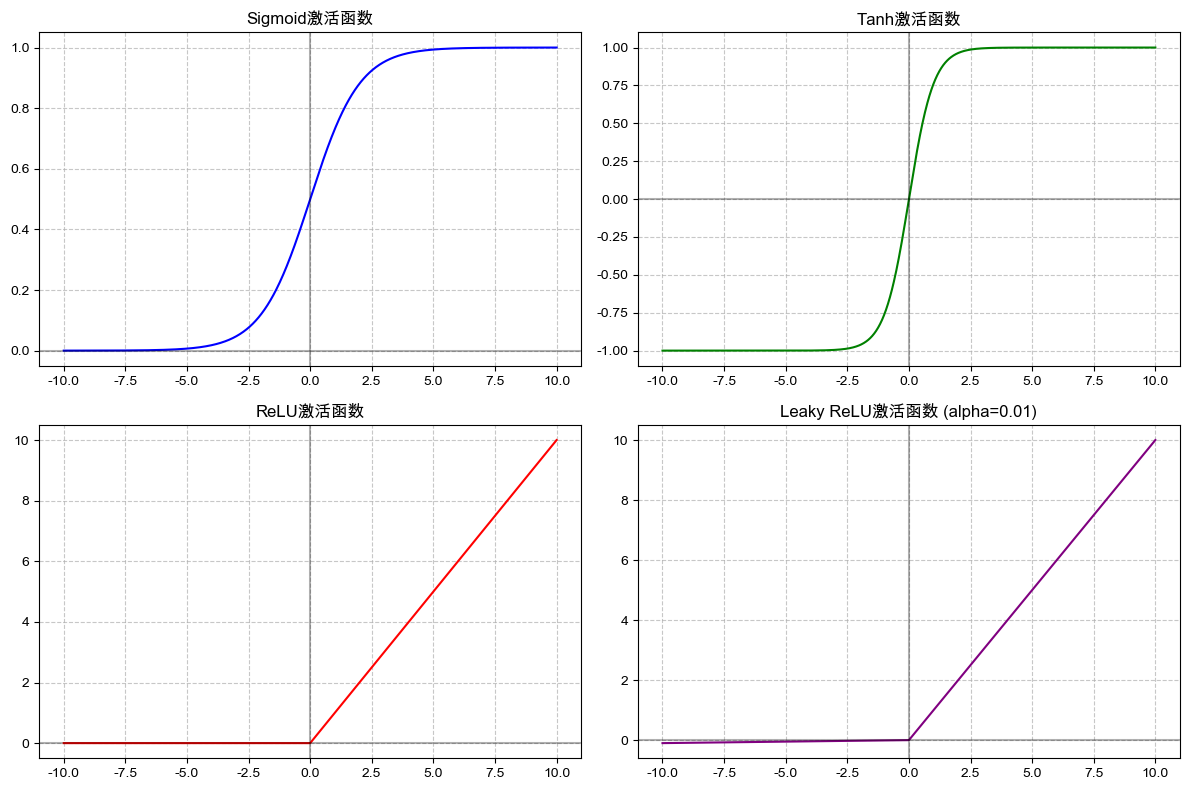
# 4. 可视化所有激活函数
plt.figure(figsize=(12, 8)) # 设置画布大小
# 子图1:Sigmoid
plt.subplot(2, 2, 1)
plt.plot(x, y_sigmoid, color='blue')
plt.title('Sigmoid激活函数')
plt.grid(True, linestyle='--', alpha=0.7)
plt.axhline(y=0, color='k', linestyle='-', alpha=0.3) # x轴
plt.axvline(x=0, color='k', linestyle='-', alpha=0.3) # y轴
# 子图2:Tanh
plt.subplot(2, 2, 2)
plt.plot(x, y_tanh, color='green')
plt.title('Tanh激活函数')
plt.grid(True, linestyle='--', alpha=0.7)
plt.axhline(y=0, color='k', linestyle='-', alpha=0.3)
plt.axvline(x=0, color='k', linestyle='-', alpha=0.3)
# 子图3:ReLU
plt.subplot(2, 2, 3)
plt.plot(x, y_relu, color='red')
plt.title('ReLU激活函数')
plt.grid(True, linestyle='--', alpha=0.7)
plt.axhline(y=0, color='k', linestyle='-', alpha=0.3)
plt.axvline(x=0, color='k', linestyle='-', alpha=0.3)
# 子图4:Leaky ReLU
plt.subplot(2, 2, 4)
plt.plot(x, y_leaky_relu, color='purple')
plt.title('Leaky ReLU激活函数 (alpha=0.01)')
plt.grid(True, linestyle='--', alpha=0.7)
plt.axhline(y=0, color='k', linestyle='-', alpha=0.3)
plt.axvline(x=0, color='k', linestyle='-', alpha=0.3)
# 调整子图间距
plt.tight_layout()
plt.show()
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容


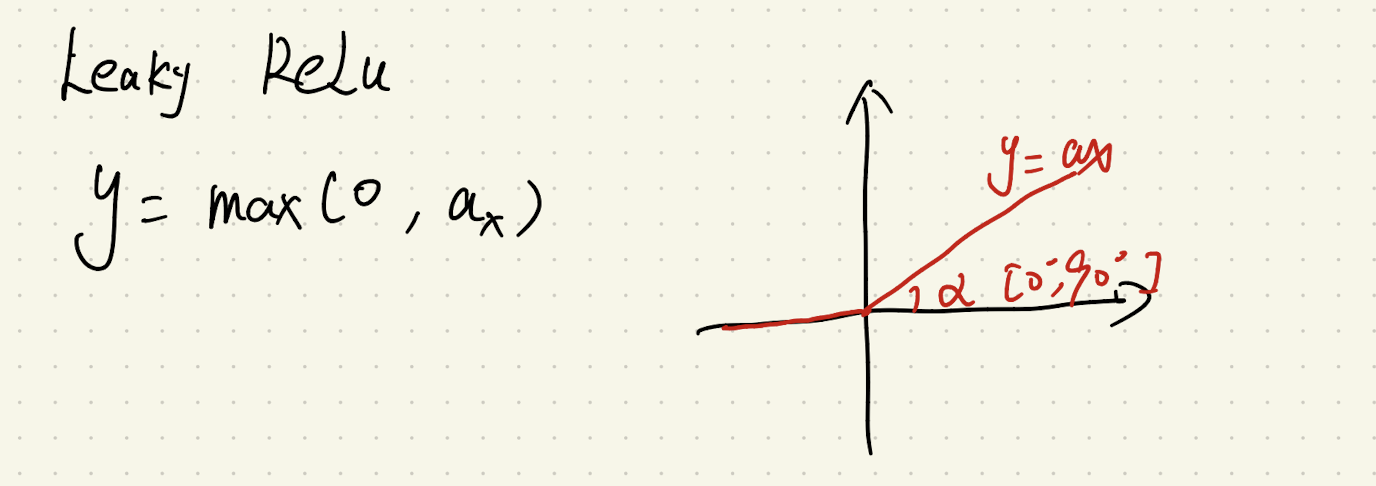






所有评论(0)