[进化算法]基于EA方案的大模型剪枝

本文提出了一种基于进化算法(EA)的神经网络架构搜索方法search-llm，用于高效裁剪大语言模型。该方法通过权重重要性计算初始化子网结构，利用改进的掩码变异算法进行全局搜索，并采用ADMM重构算法仅需少量样本即可优化权重。实验表明，search-llm能在保持原始模型性能的同时实现推理加速，且无需完整重训练。核心创新包括掩码共享机制和基于行列重要性的结构初始化策略，为LLM轻量化提供了一种新颖

ViperL1

298人浏览 · 2025-10-05 21:37:46

ViperL1 · 2025-10-05 21:37:46 发布

原文：

Search for Efficient Large Language Modelshttps://proceedings.neurips.cc/paper_files/paper/2024/hash/fb64a43508e0cfe53ee6179ff31ea900-Abstract-Conference.html代码：

search-llmhttps://github.com/shawnricecake/search-llm

一、概述

由于模型剪枝天生是一种不连续，不可微的任务。基于EA（进化算法）的方案更适合这类任务，可以不进行额外适配直接使用。本文提出了一种基于EA用于裁剪大语言模型的NAS算法，称为search-llm。相较于传统NAS，该方案无需训练，可以在保持原始LLMS优势的情况下对推理进行加速。

具体的来说，该框架分为以下几步：

①通过计算权重的重要性来确定合适的初始框架；

②基于EA从初始化子网开始全局搜索有效子网（每一代使用变异和交叉生成候选结构）；

③使用少量训练样本对候选网络进行评价，在此基础上对其进行适应度筛选；

为了有效的实现上述步骤，本文引入了两项改进：①一种掩码变异算法，用于识别详细的信道索引（传统NAS仅变异信道数目）；②基于乘子交替方向法（ADMM）的重构算法，可以仅用128个训练样本进行权值校正的改进算法。

二、算法

search-llm的总体框架如图1所示，可见其由三个部分组成：初始化；搜索；重构。

图1. 整体框架概览

1.初始化

初始化的目的是根据原始模型的权重确定统一的继承率(inheriting ratio)，该方法可以有效降低搜索代价，提高搜索性能。整个初始化算法的流程如图2所示，蓝色表示自注意力模块的掩码 $S_{attn}$ ，绿色表示MLP模块的掩码 $S_{mlp}$

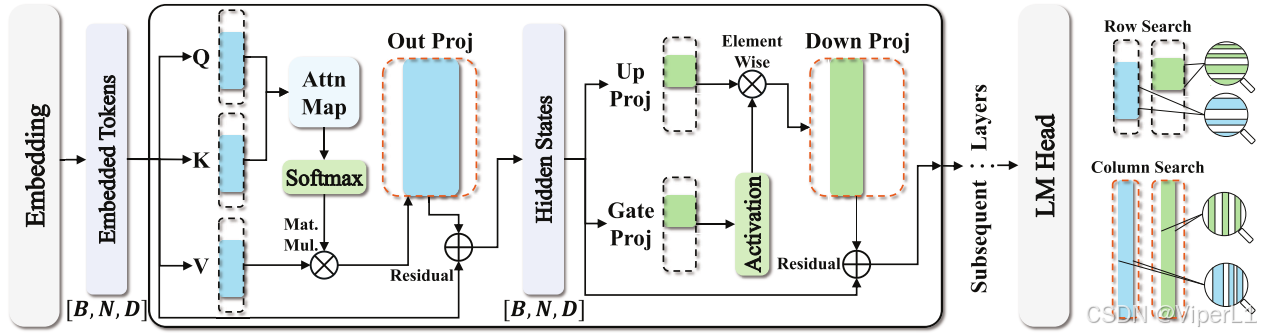
图2. 子网络结构展示

子网络结构：Transformer模块中每个模块的query,key和value的权重表述为 $W_Q$ , $W_K$ $W_V$ ，输出表述为 $W_O$ ，MLP模块中的另外三个线性层表述为 $W_U$ , $W_G$ , $W_D$ 。为了保证计算中隐藏层尺寸的一致，行的元素从 $W_Q$ , $W_K$ , $W_V$ , $W_U$ 和 $W_G$ 中选择，而列则从 $W_O$ ，和 $W_D$ 中选择。

重要性分数：反映了单独移除某个单元后造成的逐层输出最小误差（以 $l_2$ 范数计算），行列式中的重要性计算公式如下：

$[\Phi^r_W ]_i=\sum_j[\Phi]_{i,j}$ ， $[\Phi^c_W]_j=\sum_i[\Phi]_{i,j}$ ， $[\Phi]_{i,j}=\frac{[W]_{i,j}^2}{[(2XX^T)^{-1}]_{i,j}}$ .....................................①

式中 $[\Phi^r_W ]_i$ 是第 $i$ 行的重要性分数， $[\Phi^c_W]_j$ 是第 $j$ 列的重要性分数， $[\Phi]_{i,j}$ 是第 $i$ 行第 $j$ 列的重要性分数， $X$ 是输入。

掩码共享：通过行列分数，可以使用两种编码描述结构信息，即自注意力模块掩码 $S_{attn}$ 和MLP模块编码 $S_{mlp}$ ，同一模块中的不同层之间共享同一组掩码，分别将它们最小化如下所示：

$\underset{S_{attn}}{min}||S_{attn}\odot (\Phi^r_{W_Q}+\Phi^r_{W_K}+\Phi^r_{W_V}+\Phi_{W_O}^c)||$ .....................................................②

$\underset{S_{mlp}}{min}||S_{mlp}\odot (\Phi^r_{W_U}+\Phi^r_{W_G}+\Phi^r_{W_D})||$ ....................................................................③

上式中的||.||表示 $l_1$ 范数， $\bigodot$ 表示逐元素乘法(element-vise multiplication)；为了获得每个模块的掩码，对式②和③计算的对应分数之和，取值较大的子网络作为初始化架构，省略其他较小的分数对应的行/列。

2.搜索

搜索时利用EA进行全局结构搜索。图3展示了对LLaMA模型中一个块搜索的过程。

2.1掩码突变

该部分的作用是在搜索过程中产生新的掩码，从而产生新的子网络来探索搜索空间。自注意模块掩码 $S_{attn}$ 的继承率表述为 $\Gamma _{attn}=\{\gamma^i_{attn}\}^h_{i=1}$ （其中 $h$ 为head的个数），MLP模块掩码 $S_{mlp}$ 的继承率表述为 $\gamma_{mlp}$ 。在变异函数 $M$ 中，原始掩码为 $S_{attn}$ 和 $S_{mlp}$ ，突变概率为 $P_m$ ，继承率为 $\gamma^i_{attn}$ 和 $\gamma_{mlp}$ ，相似率为 $\alpha$ ，整个突变函数可以表述为下面两个式子：

${S}'_{attn}=\{M(S^i_{attn},P_m,\gamma_{attn}^i,\alpha,\eta )\}^h_{i=1}$ ...................................................................④

${S}'_{mlp}=M(S_{mlp},P_m,\gamma_{mlp},\alpha,\eta)$ ..............................................................................⑤

其中 $S_{attn}^i$ 是第 $i$ 个head的掩码， $h_m$ 是head的尺寸。其具体的变异过程一个描述为伪代码：

如果输入S的继承率已经满足 $\gamma$ ，且随机生成的 $P_r$ 满足 $P_r > P_m$ ，则不进行变异，直接返回S；否则就将S的继承行或列绑定索引 $Idx_1$ ，同时将一个在 $[0,len(S)-1]$ 的随机集合绑定 $Idx_2$ 使其满足继承率 $\gamma$ ，且 $Idx_1$ 和 $Idx_2$ 的交集的相似性需要大于门控 $\alpha$ 。

2.2搜索空间

对于LLM中每个Transformer模块的权重 $S_{attn}$ 而言，有以下定义：模型深度 $d$ ，继承率 $\Gamma =\{\gamma_{attn}^i\}^h_{i=1}$ ；对于MLP模块的权重 $S_{mlp}$ 而言，继承率 $\gamma_{mlp}$ 。搜索空间而要素如表1所示。

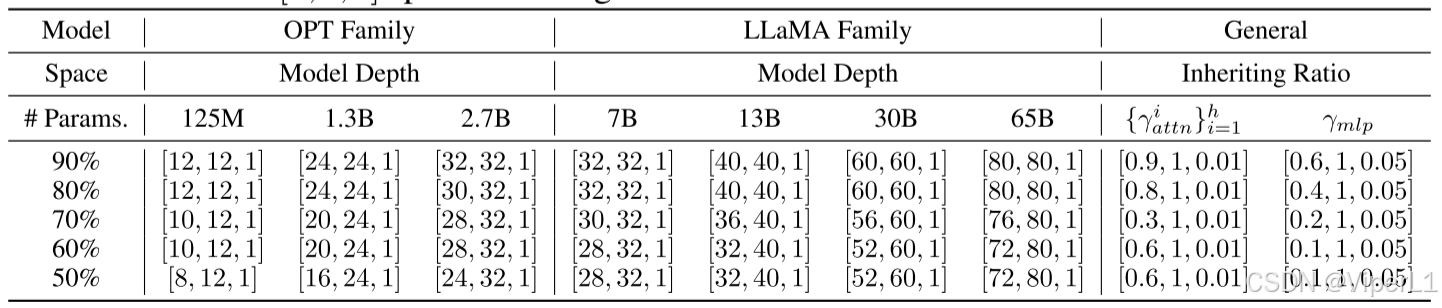
表1. 各种类型模型的搜索空间要素

需要注意的是Transformer模块的搜索空间不包含head，同时LLMs的嵌入层和输出层也不会被纳入搜索空间。

2.3搜索通道

①初始种群：对于给定的初始子网络，通过继承率和其突变概率 $P_s^0$ 和以及掩码和掩码突变率 $P_m^0$ 生成N个候选子网络。初始突变中并不涉及深度突变，候选子网络中的前 $k$ 个个体会被保留。

②搜索种群：由步骤①生成的初始种群（含 $k$ 个个体）会通过交叉和变异生成 $N$ 个候选种群。

突变：该方法随机选择父代进行突变，突变数量需要达到门限 $N_m$ 。在这一步骤中涉及深度突变，其突变概率为 $P_d$ ，同时通过概率 $P_s<P_s^0$ 改变继承率，通过概率 $P_m<P_m^0$ 使掩码突变（如式①所示）。由于这些概率都小于初始概率，可以使得优秀个体能更好的被保留。

交叉：该方法随机选择两个父样本进行交叉，直到交叉个数达到门限 $N_c$ 。

筛选：由父代生成的种群，适应度前 $k$ 个的个体会得以保留，进入下一个进化。

3.重构

是一种不需要重训练就能提高子网络性能的改造方法。使用遗漏权重的方式来改进子网络的权重，以弥补模型轻量化带来的损失。

对于子网络中线性层的原始权重 $W$ ，可以基于搜索结果掩码 $M$ 得到新权值 $\hat{W}$ 。经过此操作，线性层会输出最小化 $l_2$ 范数式 $||\hat{W}X-WX||_2^2$ ，可以描述为式⑥。

$\underset{\hat{w}}{min}||\hat{W}X-WX||_2^2$

$s.t. \hat{W}\bigodot M=0$ .........................................................................................................⑥

式⑥中， $M$ 表示修剪后权重的位置，元素1表示修剪后的权重，0表示未修剪后的权重。在这里，我们只根据W中的省略列来改革继承的列，而不是用省略的行来改造行，因为与省略的行相对应的输出总是零，这对于通过修改其他行进行的任何补偿是不可用的。为了解决这一问题，本文出了一种基于乘子交替方向法(ADMM)的解决方案，其定理如下。

北京朝阳AI社区

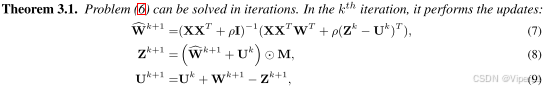
更多推荐

上下文工程驱动智能体向自动驾驶复杂场景应对

上下文工程驱动智能体向自动驾驶复杂场景应对-摘要

北京朝阳AI社区

机器学习与人工智能

python# 创建基类# 定义一对多关系# 定义多对一关系# 定义多对多关系（通过关联表）# 关联表（用于多对多关系）SQLAlchemy ORM提供了强大而灵活的数据库操作方式，通过本文的介绍，您应该能够：安装和配置SQLAlchemy定义数据模型和关系执行基本的CRUD操作构建复杂查询管理数据库事务遵循最佳实践SQLAlchemy还有更多高级特性，如混合属性、事件监听、自定义查询等，值得进一