从DQN到Double DQN:分离动作选择与价值评估,解决强化学习中的Q值过估计问题
2015年DQN在Atari游戏中突破,但Q值过估计问题浮现。因max操作放大噪声,智能体盲目自信“黄金动作”。根源在于动作选择与价值评估由同一网络完成,导致最大化偏差。
2015年DQN在Atari游戏上取得突破性进展,从此以后强化学习终于能处理复杂环境了,但没多久研究者就注意到一些奇怪的现象:
Q值会莫名其妙地增长到很大,智能体变得异常自信,坚信某些动作价值极高。实际跑起来却发现这些"黄金动作"根本靠不住,部分游戏的表现甚至开始崩盘。
问题出在哪?答案是DQN更新机制里隐藏的最大化偏差(maximization bias),这是个很微妙的统计学陷阱。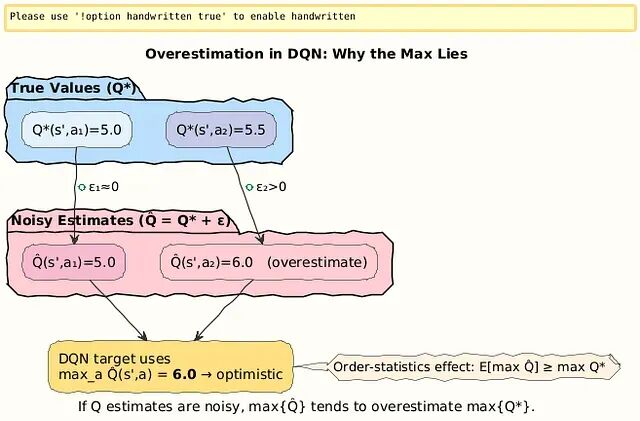
DQN的偏差来源
我们先看DQN的目标函数: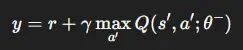
这里有个致命问题:用同一套Q值既做动作选择又做价值评估。
当Q值本身带噪声时(神经网络近似必然有噪声),max操作会系统性地挑出那些被高估的值。就像让10个人猜股价,真实价格50块,猜测结果分散在45到55之间,取最大值55肯定会偏高。
设 \hat{Q}(s, a) 是真实值 Q^*(s, a) 的噪声估计,噪声项 ε_a 均值为零。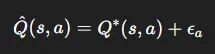
DQN的目标值: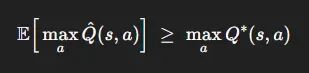
这个不等式源于序统计量的经典结果——噪声估计的最大值天然向上偏移。
Double Q-learning的核心思路
Double Q-learning给出了解法:把选择和评估分开。
用一个网络选动作而用另一个网络评估这个动作的价值,这样就避免了单个网络自我强化误差的问题。
Double DQN的更新规则
改进后的目标函数: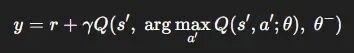
具体分工是:
- 在线网络 Q(·; θ) 负责选动作
- 目标网络 Q(·; θ^-) 负责评估价值
- 网络结构完全相同,只是在公式里扮演不同角色
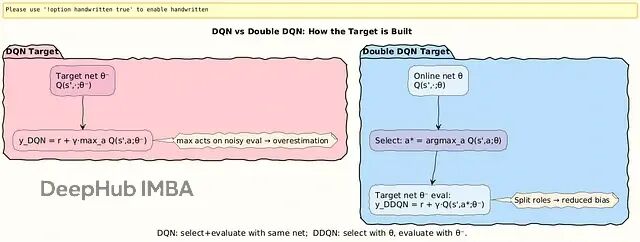
整个训练过程如下:
初始化经验池D,在线网络 Q(s, a; θ) 和目标网络 Q(s, a; θ^−)。
每个episode里循环执行:用ε-greedy策略从在线网络选动作,执行后观察奖励r和新状态s′,把这条经验存进池子。然后从池里随机采样一批数据,用DDQN规则算目标值,对下面这个损失做梯度下降: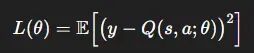
隔C步同步一次参数:θ^− ← θ。
数值例子说明
1、原始DQN的过估计
假设下个状态的Q值估计:
在线网络/目标网络给出:
- Q(s′, a_1) = 5.0
- Q(s′, a_2) = 6.0
而真实价值其实是:
- Q^∗(s′, a_1) = 5.0
- Q^∗(s′, a_2) = 5.5
取奖励r = 1,折扣因子γ = 0.9。
DQN计算的目标:
真实应该是: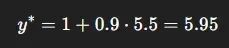
偏差达到 6.4 − 5.95 = 0.45,智能体认为动作比实际好得多。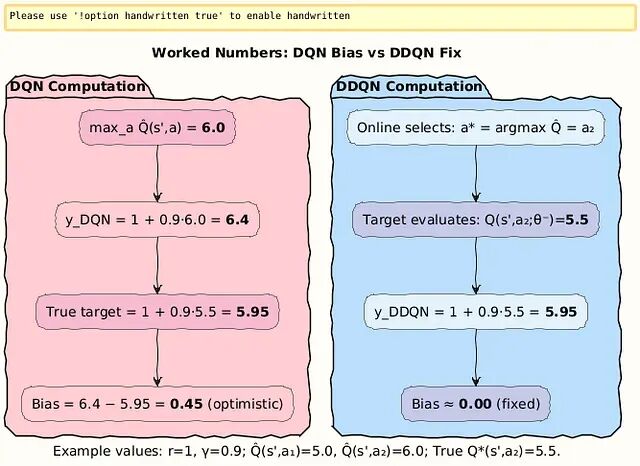
2、Double DQN如何修正
同样的场景DDQN分离了选择和评估过程。
第一步,在线网络选出最优动作: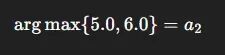
**第二步,目标网络评估这个动作的价值:**假设目标网络估计 Q(s′, a_2; θ^−) = 5.5。
第三步,计算DDQN目标: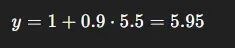
这次结果完全准确,过估计消失了。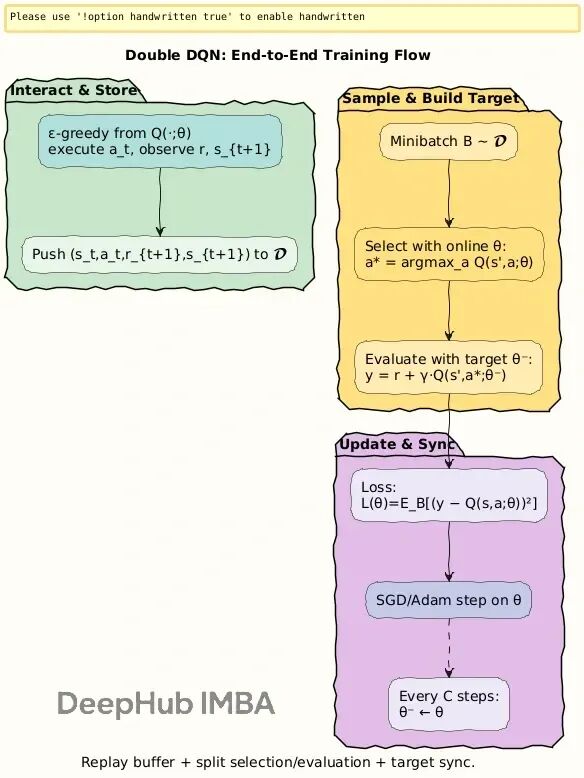
总结
这个看似简单的改动带来了明显的提升:Atari游戏分数大幅上涨,智能体不再出现那种"幻觉式"的高估,训练稳定性也改善不少。
强化学习就是这样,一个很小的数学调整可能就能解决大问题。
DQN的过估计源于max操作符偏好噪声中的高值。Double DQN把动作选择(在线网络θ)和价值评估(目标网络θ^−)分开处理,让目标值更接近真实情况,稳定性和性能都得到改善。前面两个数值例子清楚展示了偏差是如何被消除的。
作者:Satyam Mishra
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容






所有评论(0)