人工智能-机器学习day5
从无标签数据中自动发现隐藏模式和结构。
一、逻辑回归
逻辑回归是一种基于概率的分类算法,虽然名称包含"回归",但实际解决的是分类问题。其核心思想是通过线性组合特征值,再经过sigmoid函数映射到[0,1]区间,得到样本属于某个类别的概率。
1、原理
逻辑回归的输入是线性回归的输出
线性回归: h(w)=w_1x_1+w_2x_2+....+b
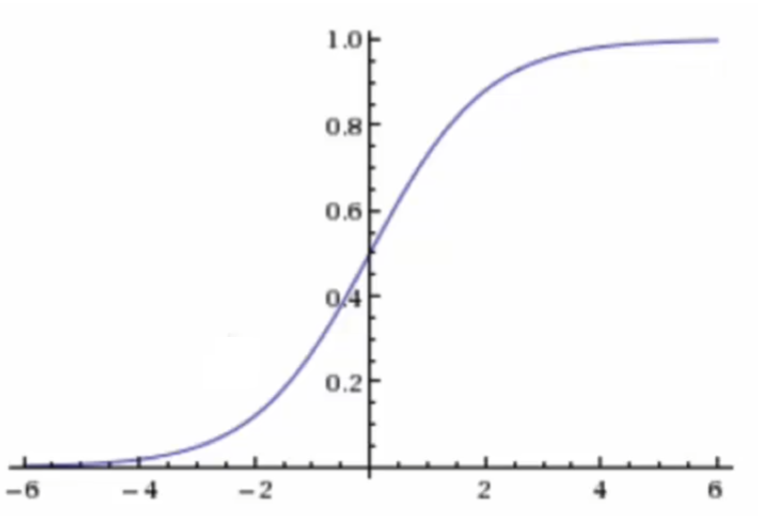
sigmoid激活函数 :f(x)=\frac{1}{1+e^{-x}}
sigmoid函数的值是在[0,1]区间中的一个概率值,默认为0.5为阈值可以自己设定,大于0.5认为是正例,小于则认为是负例
把上面的h(w) 线性的输出再输入到sigmoid函数当中 f(w)=\frac{1}{1+e^{-h(w)}}
损失函数:
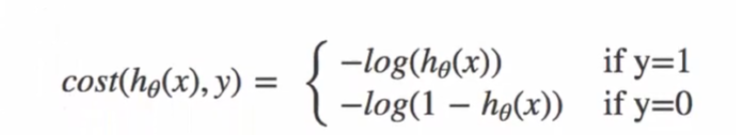
-
当y=1时,我们希望h\theta(x) 值越大越好
-
当y=0时,我们希望h\theta(x) 值越小越好
-
凸函数:保证梯度下降能找到全局最优解
综合可得:
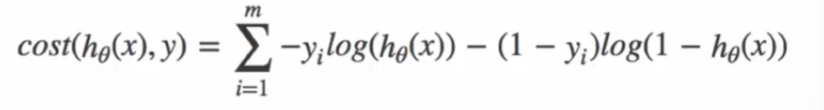
2、API
sklearn.linear_model.LogisticRegression
class sklearn.linear_model.LogisticRegression( penalty='l2', # 正则化项 *, dual=False,# 是否使用对偶问题 tol=0.0001,# 停止迭代的误差阈值 C=1.0,# 正则化强度 fit_intercept=True,# 是否计算截距 intercept_scaling=1,# 截距缩放 class_weight=None,# 权重 random_state=None,# 随机数种子 solver='lbfgs',# 优化算法 max_iter=100,# 最大迭代次数 multi_class='auto',# 多分类问题 verbose=0,# 输出信息 warm_start=False, n_jobs=None, l1_ratio=None# L1正则化 )
关键参数:
| 参数 | 类型/选项 | 默认值 | 说明 |
|---|---|---|---|
penalty |
{'l1', 'l2', 'elasticnet', None} | 'l2' | 正则化类型: - 'l1': L1正则化(特征选择) - 'l2': L2正则化(默认) - 'elasticnet': L1和L2混合 - None: 无正则化 |
C |
float | 1.0 | 正则化强度的倒数(越小表示正则化越强) |
fit_intercept |
bool | True | 是否计算截距项(偏置) |
max_iter |
int | 100 | 最大迭代次数(优化算法停止条件之一) |
solver |
{'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'} | 'lbfgs' | 优化算法: - 'liblinear': 小数据集首选 - 'lbfgs': 中等数据集(默认) - 'sag'/'saga': 大数据集 - 'newton-cg': 多分类问题 |
class_weight |
dict, 'balanced' or None | None | 类别权重: - None: 所有类权重为1 - 'balanced': 自动调整权重与类别频率成反比 - dict: 自定义权重(如{0:0.6, 1:0.4}) |
random_state |
int, RandomState instance | None | 随机种子(用于'sag'、'saga'和'liblinear') |
multi_class |
{'auto', 'ovr', 'multinomial'} | 'auto' | 多分类策略: - 'ovr': 一对多 - 'multinomial': 多项损失(softmax) - 'auto': 根据数据自动选择 |
l1_ratio |
float | None | ElasticNet混合比例(0≤l1_ratio≤1) - 仅当penalty='elasticnet'时有效 |
tol |
float | 1e-4 | 优化算法的停止容差 |
warm_start |
bool | False | 是否重用前一次调用的解决方案 |
n_jobs |
int | None | 并行计算的核心数(-1表示使用所有核心) |
| 方法 | 说明 |
|---|---|
fit(X, y[, sample_weight]) |
训练逻辑回归模型 |
predict(X) |
预测类别标签 |
predict_proba(X) |
预测类别概率(返回形状:(n_samples, n_classes)) |
predict_log_proba(X) |
预测类别概率的对数 |
score(X, y[, sample_weight]) |
返回预测的准确率 |
decision_function(X) |
预测样本的置信度分数 |
get_params([deep]) |
获取模型参数 |
set_params(**params) |
设置模型参数 |
编写代码思路参考:
1、加载数据
2、二分类
3、数据集划分
4、创建逻辑回归模型
5、训练
6、输出训练结果
7、预测
8、评估
示例代码:
#逻辑回归 from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.datasets import load_iris #1.加载数据集 iris = load_iris() X, y = iris.data, iris.target #2.数据集划分 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=22) #3.创建逻辑回归模型 model = LogisticRegression(max_iter=1000) model.fit(X_train, y_train) #4.预测 score=model.score(X_test,y_test) print(score) x_new=[[5,5,4,2], [1,1,4,3]] y_predict = model.predict(x_new) y_por=model.predict_proba(x_new) print(y_predict) print(y_por) print(model.coef_) print(model.intercept_) # 输出: # 0.9333333333333333 # [1 2] # [[0.42002736 0.42386003 0.15611261] # [0.00245963 0.02005505 0.97748532]] # [[-0.40112983 0.90486156 -2.34899221 -1.00643945] # [ 0.50868795 -0.46199865 -0.18937899 -0.74522366] # [-0.10755813 -0.44286291 2.5383712 1.75166311]] # [ 9.21707535 2.35048644 -11.56756179]
二、无监督学习 - K-means算法
1、无监督学习
无监督学习(Unsupervised Learning)计算机根据样本的特征或相关性,实现从样本数据中训练出相应的预测模型
1.无监督学习核心概念
-
核心定义:从无标签数据中自动发现隐藏模式和结构
-
核心任务:聚类、降维、异常检测等
-
关键特点:
-
只需特征矩阵 X,无需标签 y
-
算法自主识别数据内在结构
-
适用于探索性数据分析和特征发现
-
2. 聚类算法本质
-
目标:将数据划分为有意义的簇(group)
-
核心原则:簇内差异小,簇外差异大
-
评估指标:样本点到簇质心的距离
-
VS 分类算法:
-
聚类:无预定义标签,发现未知分组
-
分类:有预定义标签,预测已知类别
-

2、K - means算法
-
K-means 是一种流行的聚类算法,主要用于无监督学习中对未标记的数据进行分类。该算法的目标是将数据集中的样本划分为K个簇,使得簇内的样本彼此之间的差异最小化。这种差异通常通过簇内所有点到该簇中心点的距离平方和来衡量
-
核心概念:
| 属性 | 含义 |
|---|---|
| 簇 | Kmeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇,直观上看来簇是一个又一个聚集一起的数据,在一个簇中的数据就认为是同一类,簇就是聚类的结果表现,其中簇的个数是一个超参数 |
| 质心 | 每个簇中所有数据的均值u,通常被称为这个簇的"质心",在二维平面中,簇的质心横坐标是横坐标的均值,质心的纵坐标是纵坐标的均值 |
-
工作流程:
-
随机初始化 K 个质心
-
将样本分配到最近质心(欧氏距离)
-
重新计算质心(簇内均值)
-
重复 2-3 步直至质心稳定
-
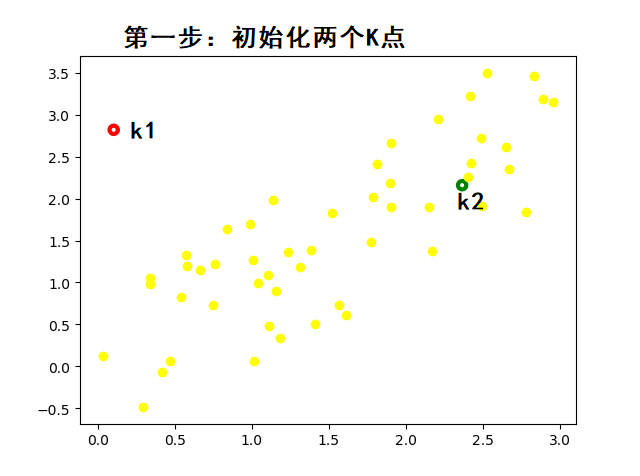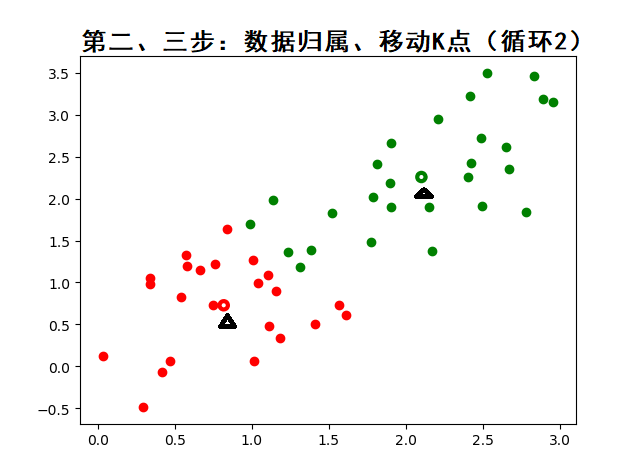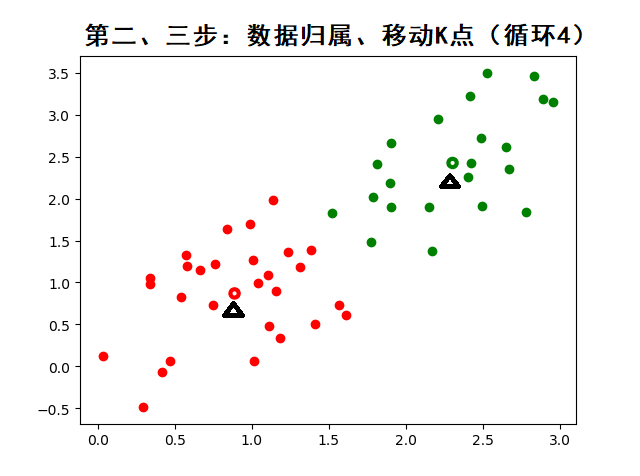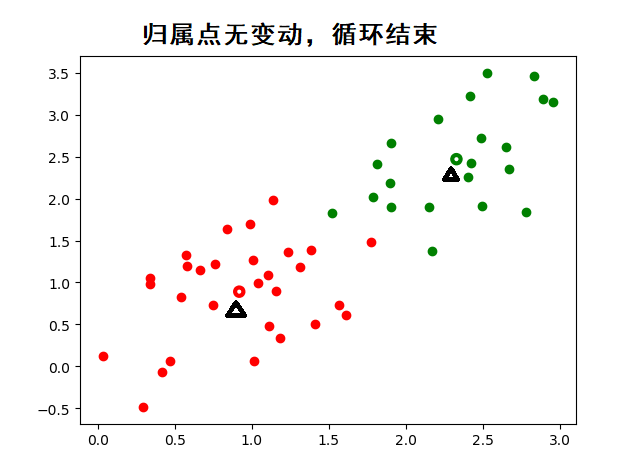
K-means 算法 API 详解(基于 scikit-learn)
1. 导入类
python
from sklearn.cluster import KMeans
2. 核心参数
| 参数 | 类型 | 默认值 | 说明 |
|---|---|---|---|
n_clusters |
int | 8 | 要形成的簇数(K值) |
init |
str | 'k-means++' | 初始化方法:'k-means++'(优化初始化)或 'random'(随机初始化) |
n_init |
int | 10 | 不同质心初始化的运行次数 |
max_iter |
int | 300 | 单次运行的最大迭代次数 |
random_state |
int/None | None | 随机种子(确保结果可复现) |
tol |
float | 1e-4 | 收敛阈值(质心变化的容忍度) |
3. 核心属性
| 属性 | 类型 | 说明 |
|---|---|---|
cluster_centers_ |
array | 聚类中心的坐标 [n_clusters, n_features] |
labels_ |
array | 每个样本的簇标签 [n_samples] |
inertia_ |
float | 样本到最近聚类中心的平方距离总和(簇内平方和) |
n_iter_ |
int | 实际迭代次数 |
make_blobs方法是 Sklearn 库中 sklearn.datasets 模块提供的一个函数,用于生成一组二维或高维的数据簇。这些数据簇通常用于聚类算法的测试。具体来说:
-
参数:
-
n_samples 参数指定了生成样本的数量
-
centers 参数定义了数据集中簇的中心数量
-
random_state 参数用于设置随机数生成器的种子,以便在不同运行之间获得相同的结果
-
-
返回值:返回一个元组
-
X:一个形状为 (n_samples, n_features) 的数组,表示生成的样本数据。每个样本都是一行,特征列为样本的各个维度坐标
-
y:一个形状为 (n_samples,) 的数组,表示每个样本所属的簇标签(中心索引)。如果不需要这个标签,可以像示例中那样用 _ 忽略它
-
4. 核心方法
python
# 拟合模型到数据 model.fit(X) # 拟合并返回簇标签(等价于 fit + labels_) labels = model.fit_predict(X) # 预测新样本所属簇 new_labels = model.predict(new_data) # 转换数据到簇距离空间(返回每个样本到每个质心的距离) distances = model.transform(X)
5. 完整使用示例
from sklearn.cluster import KMeans import matplotlib.pyplot as plt import numpy as np data=np.random.randint(0,1000,(1000,2)) # print(data) # plt.scatter(data[:,0],data[:,1]) # plt.show() # model.fit(data) n_class=7 model=KMeans(n_class) model.fit(data) # print(model.cluster_centers_) # print(model.labels_) # print(model.labels_==0) # print(data[model.labels_==0]) for i in range(n_class): point=data[model.labels_==i] plt.scatter(point[:,0],point[:,1]) # plt.scatter(model.cluster_centers_[:,0],model.cluster_centers_[:,1]) plt.show()
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容








所有评论(0)