一、机器学习

1、机器学习定义

机器学习本质上就是让计算机自己在数据中学习规律，并根据所得规律进行预测。

机器学习包括如聚类、分类、决策树、贝叶斯、神经网络、深度学习（Deep Learning）等算法

机器学习的基本过程通常包括以下几个步骤：

1. 问题定义：明确要解决的问题，确定目标。

2. 数据收集：收集与问题相关的数据。

3. 数据预处理：清洗数据、处理缺失值、异常值、数据转换、特征工程等。

4. 数据分割：将数据集划分为训练集、验证集和测试集。

5. 选择模型：根据问题类型（分类、回归、聚类等）选择合适的模型。

6. 训练模型：使用训练数据训练模型。

7. 模型评估：使用验证集评估模型性能，调整超参数。

8. 模型选择与调优：根据评估结果选择最佳模型，并进行超参数调优。

9. 模型测试：使用测试集对最终模型进行测试，评估其泛化能力。

10. 模型部署：将训练好的模型部署到实际应用中。

11. 模型监控与维护：监控模型性能，定期更新模型。

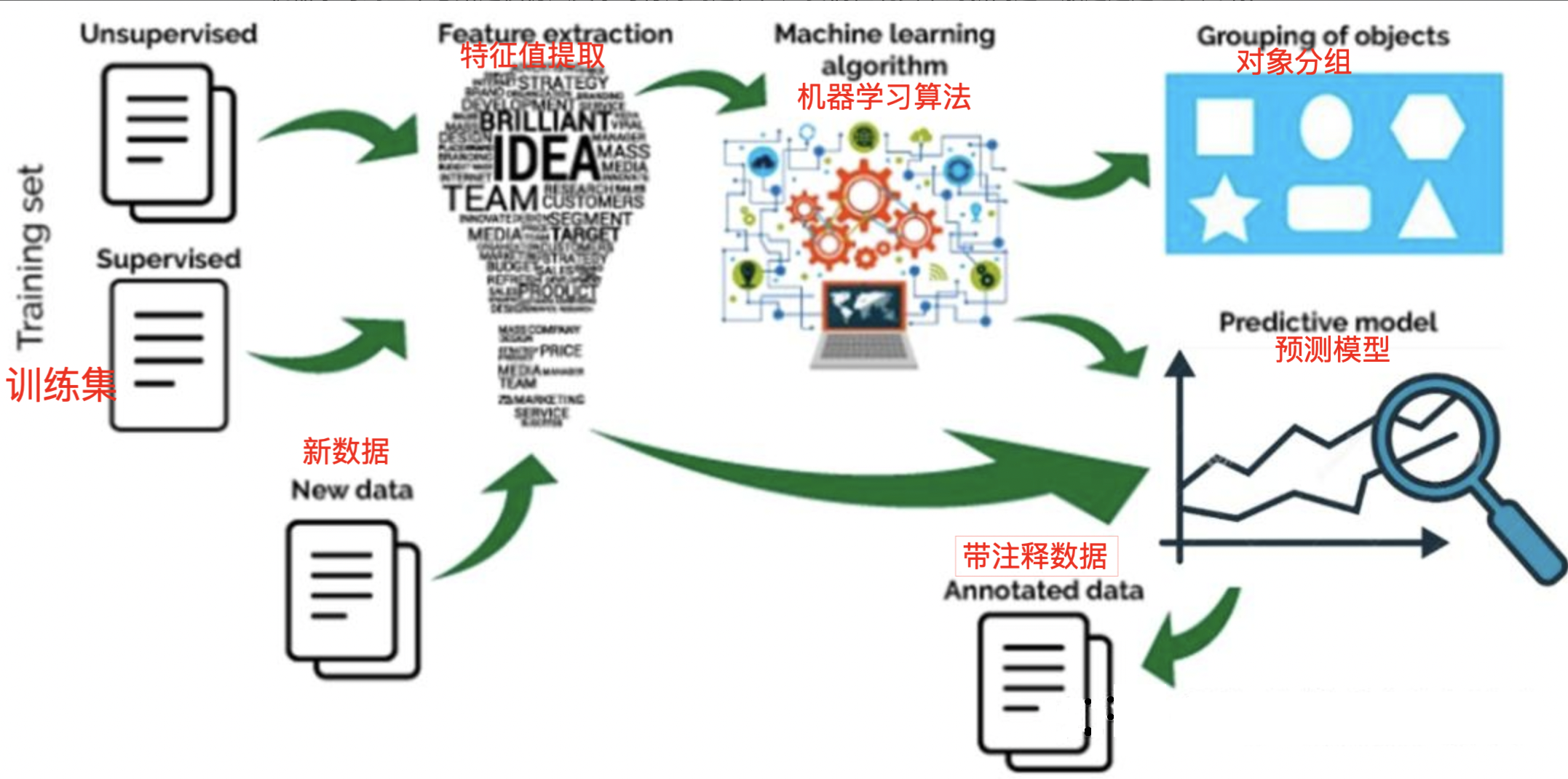
2、机器学习分类

分为监督学习，半监督学习，无监督学习和强化学习

1 监督学习

监督学习（Supervised Learning）是从有标签的训练数据中学习模型，然后对某个给定的新数据利用模型预测它的标签。如果分类标签精确度越高，则学习模型准确度越高，预测结果越精确。

监督学习主要用于回归和分类。

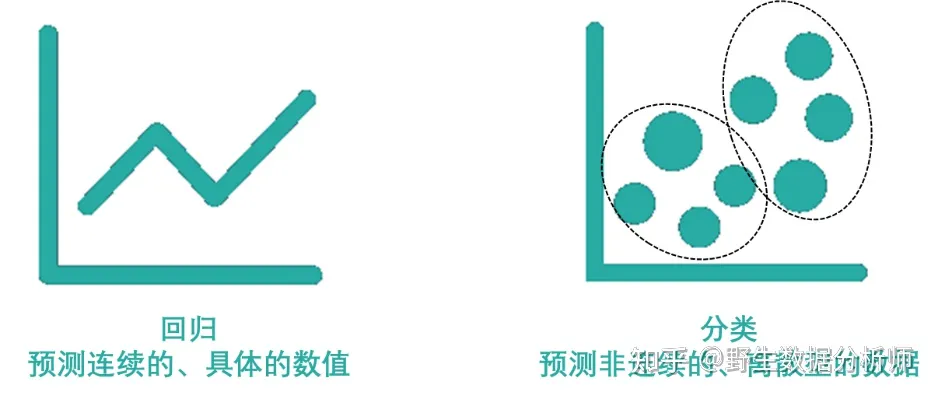
常见的监督学习的回归算法有线性回归、回归树、K邻近、Adaboost、神经网络等。

常见的监督学习的分类算法有朴素贝叶斯、决策树、SVM、逻辑回归、K邻近、Adaboost、神经网络等。

2 半监督学习

半监督学习（Semi-Supervised Learning）是利用少量标注数据和大量无标注数据进行学习的模式。

半监督学习侧重于在有监督的分类算法中加入无标记样本来实现半监督分类。

常见的半监督学习算法有Pseudo-Label、Π-Model、Temporal Ensembling、Mean Teacher、VAT、UDA、MixMatch、ReMixMatch、FixMatch等。

3 无监督学习

无监督学习（Unsupervised Learning）是从未标注数据中寻找隐含结构的过程。

无监督学习主要用于关联分析、聚类和降维。

常见的无监督学习算法有稀疏自编码（Sparse Auto-Encoder）、主成分分析（Principal Component Analysis, PCA）、K-Means算法（K均值算法）、DBSCAN算法（Density-Based Spatial Clustering of Applications with Noise）、最大期望算法（Expectation-Maximization algorithm, EM）等。

4 强化学习

强化学习（Reinforcement Learning）类似于监督学习，但未使用样本数据进行训练，是是通过不断试错进行学习的模式。

在强化学习中，有两个可以进行交互的对象：智能体（Agnet）和环境（Environment），还有四个核心要素：策略（Policy）、回报函数（收益信号，Reward Function）、价值函数（Value Function）和环境模型（Environment Model），其中环境模型是可选的。

强化学习常用于机器人避障、棋牌类游戏、广告和推荐等应用场景中。

3、机器学习应用场景

1. 自然语言处理（NLP）

   自然语言处理是人工智能中的重要领域之一，涉及计算机与人类自然语言的交互。NLP技术可以实现语音识别、文本分析、情感分析等任务，为智能客服、聊天机器人、语音助手等提供支持。

2. 医疗诊断与影像分析

   机器学习在医疗领域有着广泛的应用，包括医疗图像分析、疾病预测、药物发现等。深度学习模型在医疗影像诊断中的表现引人注目。

3. 金融风险管理

   机器学习在金融领域的应用越来越重要，尤其是在风险管理方面。模型可以分析大量的金融数据，预测市场波动性、信用风险等。

4. 预测与推荐系统

   机器学习在预测和推荐系统中也有广泛的应用，如销售预测、个性化推荐等。协同过滤和基于内容的推荐是常用的技术。

5. 制造业和物联网

   物联网（IoT）在制造业中的应用越来越广泛，机器学习可用于处理和分析传感器数据，实现设备预测性维护和质量控制。

6. 能源管理与环境保护

   机器学习可以帮助优化能源管理，减少能源浪费，提高能源利用效率。通过分析大量的能源数据，识别优化的机会。

7. 决策支持与智能分析

   机器学习在决策支持系统中的应用也十分重要，可以帮助分析大量数据，辅助决策制定。基于数据的决策可以更加准确和有据可依。

8. 图像识别与计算机视觉

   图像识别和计算机视觉是另一个重要的机器学习应用领域，它使计算机能够理解和解释图像。深度学习模型如卷积神经网络（CNN）在图像分类、目标检测等任务中取得了突破性进展。

3、机器学习项目开发步骤

1. 收集数据：无论是来自excel，access，文本文件等的原始数据，这一步（收集过去的数据）构成了未来学习的基础。相关数据的种类，密度和数量越多，机器的学习前景就越好。

2. 准备数据：任何分析过程都会依赖于使用的数据质量如何。人们需要花时间确定数据质量，然后采取措施解决诸如缺失的数据和异常值的处理等问题。探索性分析可能是一种详细研究数据细微差别的方法，从而使数据的质量迅速提高。

3. 练模型：此步骤涉及以模型的形式选择适当的算法和数据表示。清理后的数据分为两部分 - 训练和测试（比例视前提确定）; 第一部分（训练数据）用于开发模型。第二部分（测试数据）用作参考依据。

4. 评估模型：为了测试准确性，使用数据的第二部分（保持/测试数据）。此步骤根据结果确定算法选择的精度。检查模型准确性的更好测试是查看其在模型构建期间根本未使用的数据的性能。

5. 提高性能：此步骤可能涉及选择完全不同的模型或引入更多变量来提高效率。这就是为什么需要花费大量时间进行数据收集和准备的原因。

无论是任何模型，这5个步骤都可用于构建技术，当我们讨论算法时，您将找到这五个步骤如何出现在每个模型中！

二、scikit-learn

1、scikit-learn安装

参考以下安装教程：https://www.sklearncn.cn/62/

pip install -i https://pypi.tuna.tsinghua.edu.cn/simple scikit-learn

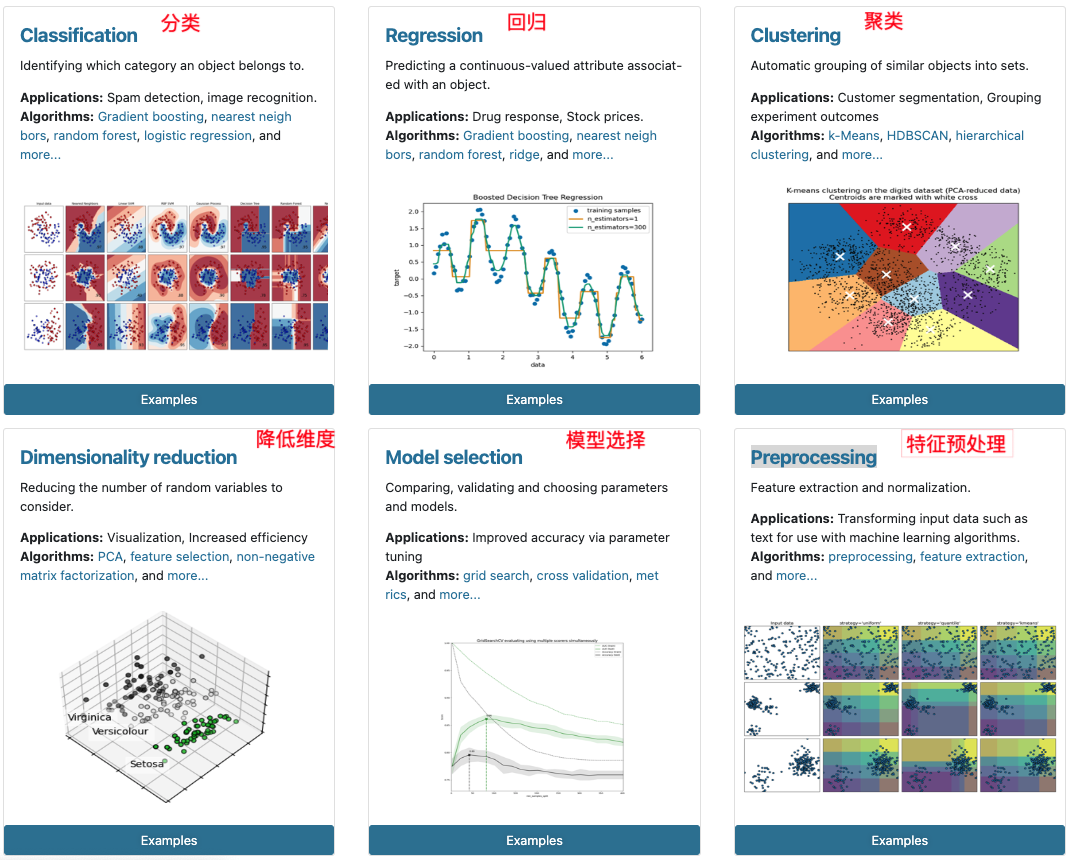
2 Scikit-learn包含的内容

三 数据集

1、 sklearn玩具数据集介绍

数据量小，数据在sklearn库的本地，只要安装了sklearn，不用上网就可以获取

2、 sklearn现实世界数据集介绍

数据量大，数据只能通过网络获取

3、 示例糖尿病数据集

代码：

from sklearn.datasets import load_diabetes
#加载数据集
diabetes=load_diabetes()
#print(diabetes)#字典
print(diabetes.data)#（特点数据，特征数据）有6个特征
print(diabetes.feature_names)  #feature_names 特征名称
print(diabetes.target)#标签（目标，结果，类别）
print(diabetes.keys())#查看可用的属性
print(diabetes.DESCR)#查看数据集的完整描述

特征有：

['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']

diabetes重要属性：

# data 特征
# feature_names 特征名称
# target  目标
# key()可用属性
# DESCR 数据集的描述
# data.shape 特征数据形状
# target.shape 标签数据形状

print(diabetes)#得到特征
print(diabetes.data)#（特点数据，特征数据）有6个特征
print(diabetes.feature_names)  #feature_names 特征名称
print(diabetes.target)#标签（目标，结果，类别）
print(diabetes.keys())#查看可用的属性
print(diabetes.DESCR)#查看数据集的完整描述
print(diabetes.data.shape)#糖尿病数据集的特征数据形状：442行，6列
print(diabetes.target.shape)#糖尿病数据集的标签数据形状：442行

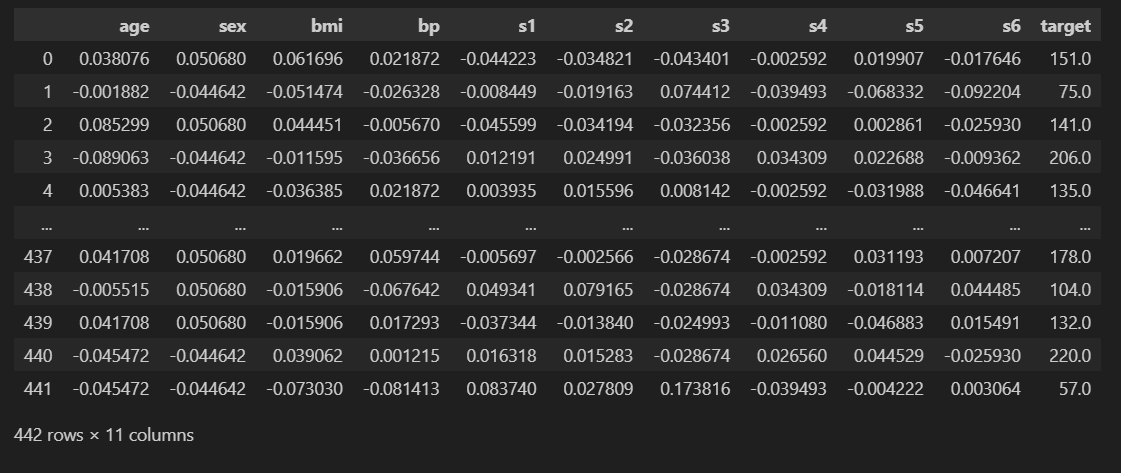
pandas把特征和目标一起显示出来：

from sklearn.datasets import load_diabetes
import numpy as np
import pandas as pd
diabetes=load_diabetes()
feature = diabetes.data
target = diabetes.target
target.shape = (len(target),1)
data = np.hstack((feature,target))
cols = diabetes.feature_names
cols.append('target')
pd.DataFrame(data,columns=cols)

4、获取现实数据集

1、导入数据集模块

from sklearn import datasets

2、加载较大现实数据集

# 加利福尼亚房价数据集 (回归问题)
california = datasets.fetch_california_housing()
​
# 20类新闻文本数据集 (分类问题)
newsgroups = datasets.fetch_20newsgroups()
​
#  Olivetti人脸数据集
faces = datasets.fetch_olivetti_faces()
​
#  Labeled Faces in the Wild人脸数据集 (更大)
lfw = datasets.fetch_lfw_people()

3、数据集的下载和缓存

首次使用fetch_*函数时会下载数据集，默认会缓存在~/scikit_learn_data目录。

自定义路径：

faces_data = fetch_olivetti_faces(data_home="./src")  # 可以指定下载路径

4、查看数据集描述

print(faces_data.DESCR)  # 打印完整数据集描述

代码：

from sklearn.datasets import fetch_olivetti_faces
from sklearn import datasets
​
# 获取Olivetti人脸数据集
faces_data = fetch_olivetti_faces(data_home="./src")  # 可以指定下载路径
​
# 查看数据集结构
print("数据集包含的对象:", faces_data.keys())
print("\n图像数据形状:", faces_data.images.shape)  # (400, 64, 64) - 400张64x64图像
print("扁平化数据形状:", faces_data.data.shape)   # (400, 4096) - 每张图像展平为4096维向量
print("\n目标标签:", faces_data.target)  # 40个人的标签(0-39)，每人10张图片
​
# 查看第一张人脸图像的数据
print("\n第一张人脸图像数据:")
print(faces_data.images[0])  # 64x64的二维数组
​
# 可视化前几张人脸
import matplotlib.pyplot as plt
​
plt.figure(figsize=(10, 8))
for i in range(12):  # 显示前12张人脸
    plt.subplot(3, 4, i+1)
    plt.imshow(faces_data.images[i], cmap=plt.cm.gray)
    plt.title(f"Person {faces_data.target[i]}")
    plt.axis('off')
plt.tight_layout()
plt.show()

1、data_home

None
    这是默认值，下载的文件路径为 “C:/Users/ADMIN/scikit_learn_data/20news-bydate_py3.pkz”
自定义路径
    例如 “./src”, 下载的文件路径为“./20news-bydate_py3.pkz”

2、subset

“train”，只下载训练集
“test”，只下载测试集
“all”， 下载的数据包含了训练集和测试集

3、return_X_y，决定着返回值的情况

False，这是默认值
True,

5、本地csv文件

(1) 创建csv文件

方式1：打开计事本，写出如下数据，数据之间使用英文下的逗号, 保存文件后把后缀名改为csv

csv文件可以使用excel打开

, milage,Liters,Consumtime,target
40920,8.326976,0.953952,3
14488,7.153469,1.673904,2
26052,1.441871,0.805124,1
75136,13.147394,0.428964,1

方式2：创建excel 文件, 填写数据，以csv为后缀保存文件

安装openpyxl模块：

pip install openpyxl

(2) pandas加载csv

使用pandas的read_csv(“文件路径”)函数可以加载csv文件，得到的结果为数据的DataFrame形式

import pandas as pd
data_f=pd.read_csv("./ss.csv")
data=data_f.to_numpy()
x=data[:,:2]
y=data[:,2]
print("x:\n",x)
print("y:\n",y)
​
​
data_f=pd.read_excel("./txt.xlsx")
print(data_f)

6、数据集划分

数据集划分是将原始数据分为训练集、验证集（可选）和测试集的过程，目的是：

• 训练集：用于模型训练（约60-80%）

• 验证集：用于调参和模型选择（约10-20%）

• 测试集：用于最终评估模型泛化能力（约10-20%）

原则：

• 测试集必须与训练集完全独立，且仅在最终评估时使用一次。

• 划分需保持数据分布一致性（如类别比例、时间顺序等）。

sklearn.model_selection.train_test_split(
    *arrays,                # 接收多个数据集（特征X、标签y等）
    test_size=None,         # 测试集比例（默认0.25）
    train_size=None,        # 训练集比例（与test_size二选一）
    random_state=None,      # 随机种子（确保可复现性）
    shuffle=True,           # 是否打乱数据（时间序列需设为False）
    stratify=None           # 按指定列分层抽样（保持类别比例）
)

参数	类型	说明
*arrays	列表/数组	支持多个输入（如特征X和标签y）
test_size	float	测试集比例（0.0-1.0）
random_state	int	固定随机种子确保结果可复现
stratify	array-like	分层抽样（通常传入标签y）

返回值

• 返回一个列表（list），长度=输入参数数量×2（每个输入被划分为训练和测试两部分）。

• 输出顺序：[X_train, X_test, y_train, y_test, ...]。

1、列表数据集划分

示例：

from sklearn.model_selection import train_test_split
​
data = [10, 20, 30, 40, 50, 60]
train, test = train_test_split(data, test_size=0.33, random_state=42)
​
print("训练集:", train)  # 例如输出: [40, 10, 50, 20]
print("测试集:", test)   # 例如输出: [60, 30]

• 直接对Python列表进行划分

• 输出仍为列表，保持原始顺序（除非设置shuffle=False）

• test_size=0.33表示测试集占33%

2、ndarray数据集划分

示例：

import numpy as np
from sklearn.model_selection import train_test_split
​
arr = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
X_train, X_test = train_test_split(arr, test_size=0.25, random_state=42)
​
print("训练集:\n", X_train)
# 输出例如:
# [[5 6]
#  [1 2]
#  [7 8]]
​
print("测试集:\n", X_test)
# 输出例如:
# [[3 4]]

• 输入为NumPy数组，输出仍为数组

• 保持二维结构不变，仅划分样本（行）

3、二维数据集划分

示例：

import numpy as np
from sklearn.model_selection import train_test_split
​
# 特征X(4个样本，每个样本3个特征)
X = np.array([[1, 2, 3], 
              [4, 5, 6],
              [7, 8, 9],
              [10, 11, 12]])
# 标签y
y = np.array([0, 1, 0, 1])
​
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.25, random_state=42
)
​
print("X_train shape:", X_train.shape)  # (3, 3)
print("y_test shape:", y_test.shape)    # (1,)

• 同时划分特征X和标签y

• 保持特征和标签的对应关系

• 二维特征数组的行（样本）被划分，列（特征）不变

4、DataFrame数据集划分

DataFrame 是一个至关重要的概念，它是 Pandas 库 里用于处理和分析结构化数据的核心数据结构。

DataFrame 是一种 二维的、表格型的数据结构，它由行和列组成，类似于 Excel 表格或者 SQL 数据库中的表。和 NumPy 的 ndarray 相比，它的优势在于可以处理 不同类型的数据（如整数、浮点数、字符串等），并且每列都有 列名。

作用：

1、数据导入和清洗

• 读取多种格式的数据：可以从 CSV、Excel、SQL 数据库等来源读取数据。

• 数据清洗：处理缺失值、重复值、异常值等

2、特征工程

• 特征选择与转换：可以方便地选择特定列、创建新特征

• 处理分类变量：将类别型特征转换为数值型（如独热编码）。

3、数据探索与可视化

• 统计分析：快速计算均值、标准差、相关性等统计量。

• 可视化：结合 Matplotlib 或 Seaborn 绘制图表。

示例：

#数据集划分：DataFrame
import pandas as pd
from sklearn.model_selection import train_test_split
​
df = pd.DataFrame({
    'age': [25, 30, 35, 40],
    'income': [50000, 60000, 70000, 80000],
    'buy': [0, 1, 0, 1]
})
​
train_df, test_df = train_test_split(
    df, test_size=0.25, random_state=42
)
​
print("训练集:")
print(train_df)
#    age  income  buy
# 1   30   60000    1
# 0   25   50000    0
# 3   40   80000    1
​
print("\n测试集:")
print(test_df)
#    age  income  buy
# 2   35   70000    0

• 直接划分Pandas DataFrame

• 保持DataFrame结构，包括列名和索引

• 适用于结构化数据预处理

5、字典数据集划分

可以划分非稀疏矩阵

用于将字典列表转换为特征向量。这个转换器主要用于处理类别数据和数值数据的混合型数据集

1.对于类别特征DictVectorizer 会为每个不同的类别创建一个新的二进制特征，如果原始数据中的某个样本具有该类别，则对应的二进制特征值为1，否则为0。

2.对于数值特征保持不变，直接作为特征的一部分

这样，整个数据集就被转换成了一个适合机器学习算法使用的特征向量形式

示例：

from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
​
data = [
    {'city': 'Beijing', 'temp': 25, 'humidity': 30},
    {'city': 'Shanghai', 'temp': 28, 'humidity': 45},
    {'city': 'Guangzhou', 'temp': 30, 'humidity': 50}
]
​
# 字典转换为数值特征
vec = DictVectorizer(sparse=False)
X = vec.fit_transform(data)
​
# 模拟标签
y = [1, 0, 1]
​
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=42
)
​
print("特征名称:", vec.get_feature_names_out())
# ['city=Beijing', 'city=Guangzhou', 'city=Shanghai', 'humidity', 'temp']
​
print("\n训练集:", X_train)
# 例如: [[ 0.  0.  1. 45. 28.]
#       [ 1.  0.  0. 30. 25.]]

• 先使用DictVectorizer将字典转换为数值矩阵

• 城市等分类变量自动进行one-hot编码

• 划分后的数据可直接用于机器学习算法

6、糖尿病数据集划分

示例：

from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
​
# 加载糖尿病数据集
diabetes = load_diabetes()
X, y = diabetes.data, diabetes.target
​
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)
​
print("训练集样本数:", X_train.shape[0])  # 353
print("测试集样本数:", X_test.shape[0])   # 89
print("特征数:", X_train.shape[1])       # 10

• 经典回归问题数据集

• 包含10个生理特征（年龄、BMI等）

• 目标变量是疾病进展指标

• 适合演示回归问题的数据划分

7、现实数据集划分

示例：

from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
import numpy as np
news = fetch_20newsgroups(data_home=None, subset='all')
list = train_test_split(news.data, news.target,test_size=0.2, random_state=22)
# """
# 返回值是一个list:其中有4个值，分别为训练集特征、测试集特征、训练集目标、测试集目标
# 与iris相同点在于x_train和x_test是列表，而iris是
# """
x_train, x_test, y_train, y_test = list
#打印结果为: 15076 3770 (15076,) (3770,)
print(len(x_train), len(x_test), y_train.shape, y_test.shape)

• 将数据集划分为训练集和测试集

• news.data: 特征数据（文本内容）

• news.target: 目标标签（新闻类别）

• test_size=0.2: 测试集占20%

• random_state=22: 固定随机种子确保结果可复现

• 返回一个包含4个元素的列表：[x_train, x_test, y_train, y_test]

• 将返回的列表解包为4个变量：

  • x_train: 训练集特征（文本）

  • x_test: 测试集特征（文本）

  • y_train: 训练集标签（类别）

  • y_test: 测试集标签（类别）

• len(x_train): 训练集样本数（15076）

• len(x_test): 测试集样本数（3770）

• y_train.shape: 训练集标签的形状（一维数组，15076个元素）

• y_test.shape: 测试集标签的形状（一维数组，3770个元素）

• random_state=22确保每次运行代码划分结果相同

数据类型	典型应用场景	划分特点	注意事项
列表	简单数据存储	保持元素类型	适合小规模非结构化数据
NumPy数组	数值计算	保持数组维度	适合矩阵运算
DataFrame	结构化数据	保留列名和索引	适合特征工程
字典数据	类别型特征	需先向量化	注意one-hot编码
糖尿病数据	回归问题	特征已标准化	目标变量需归一化
20新闻组	文本分类	文本需后续处理	注意类别平衡

四、特征工程

特征工程（Feature Engineering）是机器学习中将原始数据转化为更能代表问题本质的特征的过程，目的是通过数据转换和增强提升模型性能。它是数据预处理的核心环节，直接影响模型效果的上限。就是对特征进行相关处理。

核心目标：

• 增强数据表达：让特征更清晰地反映数据内在规律

• 提高模型效率：减少噪声和冗余，加速模型训练

• 改善泛化能力：防止过拟合，提升对新数据的预测能力

特征工程步骤为：

• 特征提取， 如果不是像dataframe那样的数据，要进行特征提取，比如字典特征提取，文本特征提取

• 无量纲化(预处理)

  • 归一化

  • 标准化

• 降维

  • 底方差过滤特征选择

  • 主成分分析-PCA降维

稀疏矩阵

稀疏矩阵是指一个矩阵中大部分元素为零，只有少数元素是非零的矩阵。在数学和计算机科学中，当一个矩阵的非零元素数量远小于总的元素数量，且非零元素分布没有明显的规律时，这样的矩阵就被认为是稀疏矩阵。例如，在一个1000 x 1000的矩阵中，如果只有1000个非零元素，那么这个矩阵就是稀疏的。

由于稀疏矩阵中零元素非常多，存储和处理稀疏矩阵时，通常会采用特殊的存储格式，以节省内存空间并提高计算效率。

三元组表 (Coordinate List, COO)：三元组表就是一种稀疏矩阵类型数据,存储非零元素的行索引、列索引和值:

(行,列) 数据

(0,0) 10

(0,1) 20

(2,0) 90

(2,20) 8

(8,0) 70

表示除了列出的有值, 其余全是0

非稀疏矩阵（稠密矩阵）

非稀疏矩阵，或称稠密矩阵，是指矩阵中非零元素的数量与总元素数量相比接近或相等，也就是说矩阵中的大部分元素都是非零的。在这种情况下，矩阵的存储通常采用标准的二维数组形式，因为非零元素密集分布，不需要特殊的压缩或优化存储策略。

• 存储：稀疏矩阵使用特定的存储格式来节省空间，而稠密矩阵使用常规的数组存储所有元素，无论其是否为零。

• 计算：稀疏矩阵在进行计算时可以利用零元素的特性跳过不必要的计算，从而提高效率。而稠密矩阵在计算时需要处理所有元素，包括零元素。

• 应用领域：稀疏矩阵常见于大规模数据分析、图形学、自然语言处理、机器学习等领域，而稠密矩阵在数学计算、线性代数等通用计算领域更为常见。

在实际应用中，选择使用稀疏矩阵还是稠密矩阵取决于具体的问题场景和数据特性。

1、特征工程API

• 实例化转换器对象，转换器类有很多，都是Transformer的子类, 常用的子类有:

  DictVectorizer  	字典特征提取
  CountVectorizer 	文本特征提取
  TfidfVectorizer 	TF-IDF文本特征词的重要程度特征提取 
  MinMaxScaler 		归一化
  StandardScaler 		标准化
  VarianceThreshold 	底方差过滤降维
  PCA  				主成分分析降维

• 转换器对象调用fit_transform()进行转换, 其中fit用于计算数据，transform进行最终转换

  fit_transform()可以使用fit()和transform()代替

  data_new = transfer.fit_transform(data)
  可写成
  transfer.fit(data)
  data_new = transfer.transform(data)

2、DictVectorizer 字典列表特征提取

API

sklearn.feature_extraction.DictVectorizer(sparse=True)

• sparse=True返回类型为csr_matrix的稀疏矩阵

• sparse=False表示返回的是数组,数组可以调用.toarray()方法将稀疏矩阵转换为数组

• 转换器对象:

  • 转换器对象调用fit_transform(data)函数，参数data为一维字典数组或一维字典列表,返回转化后的矩阵或数组

• 转换器对象get_feature_names_out()方法获取特征名

算法说明

• 输入：字典列表，每个字典表示一个样本的特征键值对

• 处理逻辑：

  1. 对所有字典的键取并集，生成特征名

  2. 数值型特征直接保留原值

  3. 类别型特征进行 One-Hot 编码（默认行为）

• 输出：稀疏矩阵或密集矩阵（数值特征 + 类别特征的二进制编码）

示例1（提取为稀疏矩阵对应的数组）：

from sklearn.feature_extraction import DictVectorizer
data=[
    {"name":"张三","age":18},
    {"name":"李四","age":19},
    {"name":"王五","age":20},
    {"name":"赵六","age":21},
    {"name":"孙七","age":22}
]
#模型研究x,y关系之前，必须保证x,y数据中全是数字
#创建转换器
transfer=DictVectorizer(sparse=False)#sparse=False表示返回的是一个完整的矩阵
data=transfer.fit_transform(data)
print(data)
print(transfer.get_feature_names_out())

输出：

[[18.  0.  1.  0.  0.  0.]
 [19.  0.  0.  1.  0.  0.]
 [20.  0.  0.  0.  1.  0.]
 [21.  0.  0.  0.  0.  1.]
 [22.  1.  0.  0.  0.  0.]]
['age' 'name=孙七' 'name=张三' 'name=李四' 'name=王五' 'name=赵六']

示例2（提取为稀疏矩阵）：

from sklearn.feature_extraction import DictVectorizer
data=[
    {"name":"张三","age":18},
    {"name":"李四","age":19},
    {"name":"王五","age":20},
    {"name":"赵六","age":21},
    {"name":"孙七","age":22}
]
#模型研究x,y关系之前，必须保证x,y数据中全是数字
#创建转换器
transfer=DictVectorizer(sparse=True)#sparse=True表示返回稀疏矩阵
data=transfer.fit_transform(data)
print(data)
print(data.toarray())#转换为数组
print(transfer.get_feature_names_out())

输出：

<Compressed Sparse Row sparse matrix of dtype 'float64'
	with 10 stored elements and shape (5, 6)>
  Coords	Values
  (0, 0)	18.0
  (0, 2)	1.0
  (1, 0)	19.0
  (1, 3)	1.0
  (2, 0)	20.0
  (2, 4)	1.0
  (3, 0)	21.0
  (3, 5)	1.0
  (4, 0)	22.0
  (4, 1)	1.0
[[18.  0.  1.  0.  0.  0.]
 [19.  0.  0.  1.  0.  0.]
 [20.  0.  0.  0.  1.  0.]
 [21.  0.  0.  0.  0.  1.]
 [22.  1.  0.  0.  0.  0.]]
['age' 'name=孙七' 'name=张三' 'name=李四' 'name=王五' 'name=赵六']

3、CountVectorizer 文本特征提取

CountVectorizer 将文本转换为词频矩阵（Bag-of-Words 模型），其工作流程如下：

1. 分词（Tokenization）

   • 默认按空格和标点分割文本（英文适用）

   • 中文需先分词（如用 jieba）

2. 构建词表（Vocabulary）

   • 统计所有文档中的唯一词项，生成词到索引的映射

3. 生成词频矩阵

   • 每行代表一个文档，每列代表一个词项

   • 矩阵值为该词在文档中出现的次数

API

sklearn.feature_extraction.text.CountVectorizer

• 构造函数关键字参数stop_words，值为list，表示词的黑名单(不提取的词)

• fit_transform函数的返回值为稀疏矩阵

算法说明

输入：

• 数据类型：字符串列表（List[str]），每个字符串代表一个文档

处理步骤：

• 分词（Tokenization）

  • 默认按空格和标点分割（英文）

  • 中文需预先分词（如 "机器学习" → "机器 学习"）

• 构建词表（Vocabulary）

  统计所有唯一词项，按字母顺序排序并编号

• 生成词频矩阵

  • 统计每个文档中每个词的出现次数

输出：

• 稀疏矩阵，密集矩阵

英文文本提取

示例:

from sklearn.feature_extraction.text import CountVectorizer
data=[
    "The quick brown fox jumps over the lazy dog.",
    "Never jump over lazy dogs quickly.",
    "Fast foxes and quick dogs are amazing."
]
counter=CountVectorizer()#创建一个计数器
data=counter.fit_transform(data)#文本词频转换为矩阵
print(data.toarray())
print(counter.get_feature_names_out())

# 输出：
# [[0 0 0 1 1 0 0 1 0 0 1 1 0 1 1 0 2]
#  [0 0 0 0 0 1 0 0 0 1 0 1 1 1 0 1 0]
#  [1 1 1 0 0 1 1 0 1 0 0 0 0 0 1 0 0]]
# ['amazing' 'and' 'are' 'brown' 'dog' 'dogs' 'fast' 'fox' 'foxes' 'jump'
#  'jumps' 'lazy' 'never' 'over' 'quick' 'quickly' 'the']

• 停用词（"the", "over", "are"等）被自动过滤

• 包含单字和双字组合（如"brown fox"）

• 矩阵值表示对应词在文档中的出现次数

中文文本提取

• 中文文本不像英文文本，中文文本文字之间没有空格，所以要先分词，一般使用jieba分词.

• 下载jieba组件, (不要使用conda)

  pip install jieba

• 可以用空格和逗号隔开

示例（空格）：

import jieba 
from sklearn.feature_extraction.text import CountVectorizer
data=[
     "我 喜欢 机器 学习",
    "深度 学习 需要 大量 数据",
    "机器 学习 和 深度 学习 都 很 有用"
]
counter=CountVectorizer()
data=counter.fit_transform(data)
print(data.toarray())
print(counter.get_feature_names_out())

# 输出：
# [[1 0 1 0 0 1 0 0]
#  [0 1 1 1 0 0 1 1]
#  [0 0 2 0 1 1 1 0]]
# ['喜欢' '大量' '学习' '数据' '有用' '机器' '深度' '需要']

示例（逗号）：

import jieba 
from sklearn.feature_extraction.text import CountVectorizer
data=[
     "我喜欢机器学习",
    "深度学习需要大量数据",
    "机器学习和深度学习都很有用"
]
counter=CountVectorizer()
data=counter.fit_transform(data)
print(data.toarray())
print(counter.get_feature_names_out())

示例（jieba）:

import jieba
from sklearn.feature_extraction.text import CountVectorizer
data = [
    "我喜欢机器学习",
    "深度学习需要大量数据",
    "机器学习和深度学习都很有用"
]

# 使用jieba进行中文分词
def chinese_tokenizer(text):
    return " ".join(jieba.cut(text))  # 用空格连接分词结果

# 预处理：对所有文本进行分词
tokenized_data = [chinese_tokenizer(text) for text in data]
print("分词结果:", tokenized_data)

# 初始化CountVectorizer，并指定自定义的分词器
counter = CountVectorizer(
    tokenizer=lambda x: x.split(),  # 按空格分割已分词的文本
    token_pattern=None             # 禁用默认的正则匹配
)

# 特征提取
X = counter.fit_transform(tokenized_data)

# 输出结果
print("\n词频矩阵:")
print(X.toarray())
print("\n特征词表:")
print(counter.get_feature_names_out())


# 输出：
# 分词结果: ['我 喜欢 机器 学习', '深度 学习 需要 大量 数据', '机器 学习 和 深度 学习 都 很 有用']

# 词频矩阵:
# [[0 1 0 1 0 1 0 0 1 0 0 0]
#  [0 0 1 1 0 0 1 0 0 1 0 1]
#  [1 0 0 2 1 0 0 1 1 1 1 0]]

# 特征词表:
# ['和' '喜欢' '大量' '学习' '很' '我' '数据' '有用' '机器' '深度' '都' '需要']

4、TfidfVectorizer TF-IDF文本特征词的重要程度特征提取

算法

词频(Term Frequency, TF), 表示一个词在当前篇文章中的重要性

逆文档频率(Inverse Document Frequency, IDF), 反映了词在整个文档集合中的稀有程度

1. 核心公式

TF-IDF = 词频(TF) × 逆文档频率(IDF)

TF (词频)：

• 基础公式：TF = 词出现次数 / 文档总词数

• sklearn默认：直接使用原始词频（未归一化）

IDF (逆文档频率)：

• 基础公式：IDF = log(总文档数 / (包含该词的文档数 + 1))

• sklearn优化公式：IDF = log((总文档数 + 1) / (包含该词的文档数 + 1)) + 1

2. sklearn的特殊处理

• 平滑处理：+1防止除零错误

• 归一化：默认对文档向量进行L2归一化

L2归一化的定义

L2归一化（也称为欧式归一化）是将向量的各维度值调整到单位长度（长度为1）的标准化方法。其核心是对向量的每个元素进行缩放，使得整个向量的 L2范数（欧几里得范数） 等于1。

在TF-IDF中，L2归一化主要用于：

1. 消除文档长度的影响： 长文档的原始TF-IDF值可能普遍偏大，归一化后不同长度的文档向量可比。

2. 方便相似度计算： 归一化后的向量，余弦相似度直接等于点积（因为向量长度均为1）。

3. 防止模型偏向长文本： 机器学习模型（如SVM）对特征尺度敏感，归一化使权重更公平。

API

sklearn.feature_extraction.text.TfidfVectorizer()

• 构造函数关键字参数stop_words，表示词特征黑名单

• fit_transform函数的返回值为稀疏矩阵

示例1：

from sklearn.feature_extraction.text import TfidfVectorizer
data=[
    "The quick brown fox jumps over the lazy dog.",
    "Never jump over lazy dogs quickly.",
    "Fast foxes and quick dogs are amazing."
]
counter=TfidfVectorizer()#创建一个计数器
data=counter.fit_transform(data)#文本词频转换为矩阵

print(data.toarray())
print(counter.get_feature_names_out())

示例2：

import jieba
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizer

# 自定义中文分词函数
def chinese_cut(text):
    return " ".join(jieba.cut(text))

# 示例文档集
documents = [
    "教育部召开民办教育发展研讨会",
    "民办教育机构获得政策扶持", 
    "教育部发布最新教育政策"
]

# 1. 中文分词处理
corpus = [chinese_cut(doc) for doc in documents]
print("分词结果：")
for i, doc in enumerate(corpus):
    print(f"文档{i+1}: {doc}")

# 2. TF-IDF向量化
tfidf = TfidfVectorizer(
    stop_words=["召开", "获得"],  # 自定义停用词
    max_features=5              # 只保留最重要的5个特征
)

# 3. 拟合并转换数据
X = tfidf.fit_transform(corpus)

# 4. 结果展示
df = pd.DataFrame(
    X.toarray().round(3),
    columns=tfidf.get_feature_names_out(),
    index=[f"文档{i+1}" for i in range(len(documents))]
)

print("\nTF-IDF矩阵：")
print(df)

• 文档1中"教育部"权重最高（0.795），因为：

• 在文档1中出现1次（TF=1）

• 在3个文档中出现2次（IDF=log(4/3)+1≈1.29）

• 未归一化值：1 × 1.29 = 1.29

• 经过L2归一化后得到0.795

5、无量纲化-预处理

1.无量纲化核心概念

为什么要无量纲化？

• 问题：不同特征的单位和量级差异导致模型偏向大数值特征（如收入 vs 身高）

• 解决：通过缩放使所有特征处于同一量级，提升模型公平性和收敛速度

方法分类

方法	缩放方式	适用场景	鲁棒性
归一化	按最大值最小值线性缩放	数据分布边界明确（如图像像素）	差（受异常值影响大）
标准化	按均值和标准差缩放	数据符合正态分布	强
L2归一化	使向量长度为1（欧式归一化）	文本向量、距离计算	中等

2. MinMax归一化（MinMaxScaler）

公式

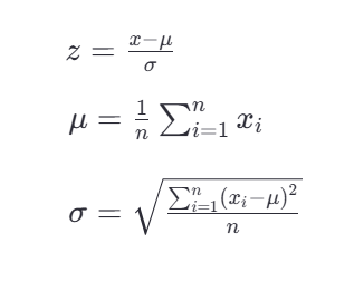
这里的 𝑥min 和 𝑥max 分别是每种特征中的最小值和最大值，而 𝑥是当前特征值，𝑥scaled 是归一化后的特征值。

若要缩放到其他区间，可以使用公式：x=x*(max-min)+min;

比如 [-1, 1]的公式为：

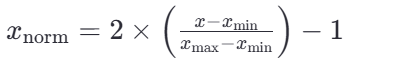
API

sklearn.preprocessing.MinMaxScaler(feature_range)

参数:feature_range=(0,1) 归一化后的值域,可以自己设定

fit_transform函数归一化的原始数据类型可以是list、DataFrame和ndarray, 不可以是稀疏矩阵

fit_transform函数的返回值为ndarray

示例:

from sklearn.preprocessing import MinMaxScaler
import numpy as np

data = np.array([[1.75, 15000, 120], 
                 [1.50, 16000, 140],
                 [1.60, 20000, 100]])

# 缩放到[0,1]区间
scaler = MinMaxScaler(feature_range=(0, 1))
scaled_data = scaler.fit_transform(data)

print("归一化结果:\n", scaled_data)

# 输出：
# 归一化结果:
#  [[1.  0.  0.5]
#  [0.  0.2 1. ]
#  [0.4 1.  0. ]]

缺点

最大值和最小值容易受到异常点影响，所以鲁棒性较差。所以常使用标准化的无量钢化

3.L2归一化（Normalize）

公式

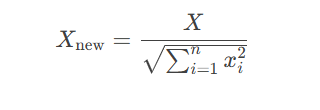
API

from sklearn.preprocessing import normalize
normalize(data, norm='l2', axis=1)
#data是要归一化的数据
#norm是使用那种归一化:"l1"  "l2"  "max
#axis=0是列  axis=1是行

L1归一化

计算逻辑：对每个样本（行）计算L1范数（绝对值之和），然后除以该范数

绝对值相加作为分母,特征值作为分子

示例：

import numpy as np
from sklearn.preprocessing import normalize

# 原始数据（3个样本，4个特征）
X = np.array([
    [1, 2, 3, 4],    # 样本1
    [5, 0, 8, 2],    # 样本2
    [0, 2, 0, 6]     # 样本3
])
X_l1 = normalize(X, norm='l1', axis=1)
print("L1归一化结果:\n", X_l1.round(4))
# 输出结果为:
# L1归一化结果:
#  [[0.1    0.2    0.3    0.4   ]
#  [0.3333 0.     0.5333 0.1333]
#  [0.     0.25   0.     0.75  ]]

L2归一化

计算逻辑：对每个样本（行）计算L2范数（欧几里得长度），然后除以该范数

平方相加作为分母,特征值作为分子

示例：

import numpy as np
from sklearn.preprocessing import normalize

# 原始数据（3个样本，4个特征）
X = np.array([
    [1, 2, 3, 4],    # 样本1
    [5, 0, 8, 2],    # 样本2
    [0, 2, 0, 6]     # 样本3
])
X_l2 = normalize(X, norm='l2', axis=1)
print("L2归一化结果:\n", X_l2.round(4))

# 输出：
# L2归一化结果:
#  [[0.1826 0.3651 0.5477 0.7303]
#  [0.5185 0.     0.8296 0.2074]
#  [0.     0.3162 0.     0.9487]]

max归一化

计算逻辑：对每个样本（行）除以该行的最大值

max作为分母,特征值作为分子

示例：

import numpy as np
from sklearn.preprocessing import normalize

# 原始数据（3个样本，4个特征）
X = np.array([
    [1, 2, 3, 4],    # 样本1
    [5, 0, 8, 2],    # 样本2
    [0, 2, 0, 6]     # 样本3
])
X_max = normalize(X, norm='max', axis=1)
print("Max归一化结果:\n", X_max.round(4))

# 输出：
# Max归一化结果:
#  [[0.25   0.5    0.75   1.    ]
#  [0.625  0.     1.     0.25  ]
#  [0.     0.3333 0.     1.    ]]

4.StandardScaler 标准化

在机器学习中，标准化是一种数据预处理技术，也称为数据归一化或特征缩放。它的目的是将不同特征的数值范围缩放到统一的标准范围，以便更好地适应一些机器学习算法，特别是那些对输入数据的尺度敏感的算法。

标准化公式

最常见的标准化方法是Z-score标准化，也称为零均值标准化。它通过对每个特征的值减去其均值，再除以其标准差，将数据转换为均值为0，标准差为1的分布。这可以通过以下公式计算:

其中，z是转换后的数值，x是原始数据的值，μ是该特征的均值，σ是该特征的 标准差

标准化 API

sklearn.preprocessing.StandardScale

• 与MinMaxScaler一样，原始数据类型可以是list、DataFrame和ndarray

• fit_transform函数的返回值为ndarray, 归一化后得到的数据类型都是ndarray

from sklearn.preprocessing import StandardScaler
#不能加参数feature_range=(0, 1)
transfer = StandardScaler()
data_new = transfer.fit_transform(data) #data_new的类型为ndarray

示例：

from sklearn.preprocessing import StandardScaler
import numpy as np

# 创建示例数据（3个样本，3个特征）
data = np.array([
    [170, 60, 25],    
    [165, 55, 30],    
    [180, 70, 20]     
])

# 初始化标准化器
scaler = StandardScaler()

# 拟合并转换数据
standardized_data = scaler.fit_transform(data)

print("原始数据:\n", data)
print("\n标准化后数据（均值=0，标准差=1）:\n", standardized_data.round(2))
print("\n各特征均值:", scaler.mean_.round(2))
print("各特征标准差:", np.sqrt(scaler.var_).round(2))

# 输出：
# 原始数据:
#  [[170  60  25]
#  [165  55  30]
#  [180  70  20]]

# 标准化后数据（均值=0，标准差=1）:
#  [[-0.27 -0.27  0.  ]
#  [-1.07 -1.07  1.22]
#  [ 1.34  1.34 -1.22]]

# 各特征均值: [171.67  61.67  25.  ]
# 各特征标准差: [6.24 6.24 4.08]

6、特征降维

实际数据中,有时候特征很多,会增加计算量,降维就是去掉一些特征,或者转化多个特征为少量个特征

特征降维其目的:是减少数据集的维度，同时尽可能保留数据的重要信息。

特征降维的好处:

减少计算成本：在高维空间中处理数据可能非常耗时且计算密集。降维可以简化模型，降低训练时间和资源需求。

去除噪声：高维数据可能包含许多无关或冗余特征，这些特征可能引入噪声并导致过拟合。降维可以帮助去除这些不必要的特征。

特征降维的方式:

• 特征选择

  • 从原始特征集中挑选出最相关的特征

• 主成份分析(PCA)

  • 主成分分析就是把之前的特征通过一系列数学计算，形成新的特征，新的特征数量会小于之前特征数量

1.特征选择

核心目标是降低数据维度、减少计算开销、提升模型性能并增强可解释性

（1）VarianceThreshold 低方差过滤特征选择

目的是移除低方差的特征

低方差过滤特征选择：（方差小，这个特征的值在样本中几乎相同或者变化不大）

Filter(过滤式): 主要探究特征本身特点， 特征与特征、特征与目标 值之间关联

主要步骤包括：计算方差，设定阈值，过滤特征

transfer = VarianceThreshold(threshold=0.1)

• 设置阈值为0.1，表示方差低于0.1的特征将被移除

• VarianceThreshold作用:

  • 移除所有方差低于阈值的特征

  • 常用于数据预处理，去除变化小的特征

• 阈值选择:

  • threshold=0.1表示只保留方差>0.1的特征

  • 如果设为0，则只移除方差为0的特征(即所有样本取值相同的特征)

data = transfer.fit_transform(data)

• 应用转换，只保留方差大于0.1的特征

示例：

from sklearn.feature_selection import VarianceThreshold

data=[[0,2,0,3],
      [0,1,4,3],
      [0,2,1,3],
      [0,2,1,5]]

transfer=VarianceThreshold(threshold=0.1)
data=transfer.fit_transform(data)
print(data)

#输出结果为：
# [[2 0 3]
#  [1 4 3]
#  [2 1 3]
#  [2 1 5]]

（2）根据相关系数的特征选择

相关系数特征选择是通过量化特征间线性关系强度来筛选特征的方法，主要基于皮尔逊相关系数（Pearson Correlation Coefficient）。该系数衡量两个变量的线性相关性，取值范围为[-1,1]：

· ρ=1：完全正相关

· ρ=-1：完全负相关

· ρ=0：无线性关系

p=pearsonr(x,y)

· 相关性类型

o 正相关：变量同向变化（如身高与体重）

o 负相关：变量反向变化（如运动频率与BMI）

o 不相关：|ρ|<0.4（如饭量与智商）

· 强度分级

o 低度相关：|ρ|<0.4

o 显著相关：0.4≤|ρ|<0.7

o 高度相关：0.7≤|ρ|≤1

示例：

#根据相关系数的特征选择
from scipy.stats import pearsonr
x=[1,2,3,4,5]
x=[5,4,3,2,1]
x=[5,6,7,3,2]
y=[1,2,3,4,5]

p=pearsonr(x,y)
print(p)

2.主成分分析（PCA）

PCA(Principal Component Analysis)是一种常用的降维技术，通过线性变换将高维数据投影到低维空间，同时保留尽可能多的数据信息。

原理：

PCA的目标是找到一个新的坐标系（主成分），使得数据在新坐标轴上的投影方差最大化。具体来说：

• 方差最大化：数据在新方向上的投影应尽可能分散（方差大），这样能保留更多信息。

• 降维：选择前几个方差最大的方向（主成分）作为新特征，舍弃方差小的方向，从而实现降维。

几何解释：

• 原始数据点在高维空间中分布，PCA试图找到一个超平面（如直线、平面），使得数据点到该超平面的垂直距离（重建误差）最小，或投影点到超平面上的方差最大。

• 例如，二维数据降为一维时，选择一条直线，使得所有数据点投影到该直线后的方差最大

PCA的步骤

1. 数据预处理：中心化（均值归零），可选标准化（方差归一化）。

2. 计算协方差矩阵：C=1/n X^T X

3. 特征值分解：得到特征值和特征向量。

4. 选择主成分：按特征值从大到小排序，保留前 kk 个。

5. 投影降维：用选定的特征向量变换原始数据。

3.API

from sklearn.decomposition import PCA

PCA(n_components=None)

• 主成分分析

• n_components:

  • 实参为小数时：表示降维后保留百分之多少的信息

  • 实参为整数时：表示减少到多少特征

示例（n_components为小数）：（保留95%信息）

#n_components为小数
from sklearn.decomposition import PCA

def pca_demo():
    data = [[2,8,4,5], 
            [6,3,0,8], 
            [5,4,9,1]]
    
    # 实例化转换器，保留95%的信息
    transfer = PCA(n_components=0.95)
    
    # 执行降维
    data_new = transfer.fit_transform(data)
    print("降维结果:\n", data_new)
    print("各主成分解释的方差比例:", transfer.explained_variance_ratio_)
    print("累计解释方差比例:", sum(transfer.explained_variance_ratio_))

pca_demo()

# 输出：
# 降维结果:
#  [[-1.28620952e-15  3.82970843e+00]
#  [-5.74456265e+00 -1.91485422e+00]
#  [ 5.74456265e+00 -1.91485422e+00]]
# 各主成分解释的方差比例: [0.75 0.25]
# 累计解释方差比例: 1.0

示例（n_components为整数）：

from sklearn.decomposition import PCA
import numpy as np

# 创建示例数据集（4个特征，5个样本）
data = np.array([
    [1.0, 2.5, 3.0, 4.8],
    [2.0, 3.5, 2.8, 5.2],
    [0.5, 2.0, 3.5, 4.5],
    [1.5, 3.0, 3.2, 5.0],
    [0.8, 2.2, 3.8, 4.9]
])

print("原始数据形状:", data.shape)  # (5, 4)

# 创建PCA转换器，降维到2个主成分
pca = PCA(n_components=2)  # 明确设置为整数2

# 拟合数据并转换
data_pca = pca.fit_transform(data)

print("\n降维后的数据形状:", data_pca.shape)  # (5, 2)
print("\n降维后的数据:")
print(data_pca)

# 查看各主成分解释的方差比例
print("\n各主成分解释的方差比例:", pca.explained_variance_ratio_)
print("累计解释方差比例:", sum(pca.explained_variance_ratio_))


# 输出：
# 原始数据形状: (5, 4)

# 降维后的数据形状: (5, 2)

# 降维后的数据:
# [[-1.20820327e-01 -3.11855739e-01]
#  [ 1.32632903e+00  4.38177841e-04]
#  [-1.00814572e+00 -1.55286256e-01]
#  [ 4.98318094e-01  1.08765703e-01]
#  [-6.95681077e-01  3.57938114e-01]]

# 各主成分解释的方差比例: [0.9259719 0.0686955]
# 累计解释方差比例: 0.9946674053364086