🏆 本文收录于 《YOLOv8实战：从入门到深度优化》，该专栏持续复现网络上各种热门内容(全网YOLO改进最全最新的专栏，质量分97分+，全网顶流)，改进内容支持(分类、检测、分割、追踪、关键点、OBB检测)。且专栏会随订阅人数上升而涨价(毕竟不断更新)，当前性价比极高，有一定的参考&学习价值，部分内容会基于现有的国内外顶尖人工智能AIGC等AI大模型技术总结改进而来，嘎嘎硬核。
  
✨ 特惠福利：目前活动一折秒杀价！一次订阅，永久免费，所有后续更新内容均免费阅读！

⏩ 0. 摘要

  大家好呀！欢迎回到《YOLOv8专栏》的探索之旅！👋 在之前的章节中，我们探讨了通过稀疏化来为模型“瘦身”的技术。而今天，我们将把轻量化推向一个令人惊叹的极限——二值神经网络（BNN）。想象一下，如果模型中所有的权重和激活值不再是32位的浮点数，而是仅仅由 +1 和 -1 构成，这将带来多大的存储和计算优势？BNN正是这样一种技术，它将神经网络压缩到了1-bit的极致。

  这不仅意味着模型体积可以缩小32倍，更重要的是，昂贵的乘加运算（MAC）可以被高效的位运算（XNOR和bitcount）所取代！本文将带你深入BNN的核心，从权重与激活的二值化策略，到解决梯度消失难题的“魔法”——直通估计器（STE），再到弥补精度损失的各种实用技巧。

  最终，我们将手把手教你构建一个二值化卷积模块，并探讨如何将其集成到YOLOv8中。准备好进入这个充满挑战与机遇的1-bit世界了吗？让我们一起见证极限压缩压缩的魅力！🌟

⏩ 1. 上期回顾：Sparse Convolution稀疏卷积优化

  👋 在上一节 《YOLOv8【卷积创新篇·第27节】Sparseonvolution稀疏卷积优化》 中，我们一起探索了如何利用“稀疏性”来加速和压缩我们的模型。我们了解到，无论是激活值的稀疏性（很多值接近于零），还是权重的稀疏性（很多参数可以被裁剪），都为我们提供了优化的空间。通过稀疏卷积，我们可以在不牺牲太多精度的情况下，跳过大量无效的计算，从而提升模型的推理效率。

  稀疏化和我们今天要讨论的量化，是模型优化的两大主流方向。稀疏化关注的是“减少计算量”，而量化关注的是“降低计算和存储的精度”。今天，我们将把量化这个思想推向极致——二值化，看看当整个网络的数值都变成1-bit时，会发生怎样奇妙的化学反应！准备好了吗？Let’s Go! 🚀

⏩ 2. 核心思想：走向1-bit的极限压缩

2.1 为什么需要二值化？浮点数的“不能承受之重”

  我们通常使用的神经网络，其权重和激活值都是以32位浮点数（FP32）的形式存储和计算的。一个FP32数值需要占用4个字节（32 bits）的存储空间。对于像YOLOv8这样动辄数千万参数的大模型来说，这意味着：

• 巨大的存储开销：一个拥有5000万参数的模型，仅存储权重就需要 50,000,000 * 4 bytes ≈ 200 MB 的空间。这对于存储资源极其有限的微控制器（MCU）或物联网（IoT）设备来说是难以承受的。
• 高昂的计算：浮点数的乘加运算（MAC）在硬件上是相对复杂的计算单元，功耗和延迟都比较高。

二值神经网络inary Neural Network, BNN） 提出了一种激进的解决方案：将权重和中间的激活值全部量化为 +1 和-1`。

  这意味着每个数值只需要 1-bit 来存储！这将带来革命性的优势：

1. **极致的存储压缩：相比FP32，模型大小直接减少 32倍！200MB的模型瞬间可以压缩到约6.25MB。
2. 计算效率的飞跃：当权重和激活值都变成 +1 和 -1 后，原本的乘法运算可以被硬件上极其高效的 按位异或非（XNOR） 操作替代。加法可以被 比特计数（bitcount） 替代。这使得BNN在定制硬件（如FPGA）上运行时，能效比极高。

2.2 BNN的两大基石：权重与激活的二值化

  BNN的核心思想简单而优雅，它主要建立在两个基本操作之上：

• 权重二值化 (Weight Binarization)：在模型进行前向传播时，将全精度的权重实时地二值化为 +1 或 -1。
• 激活二值化 (Activation Binarization)：在前向传播过程中，每个卷积层或全连接层的输出（在送入下一个层之前）也要被二值化为 +1 或 -1。

  我们可以用下面的流程图来形象地展示这个过程：

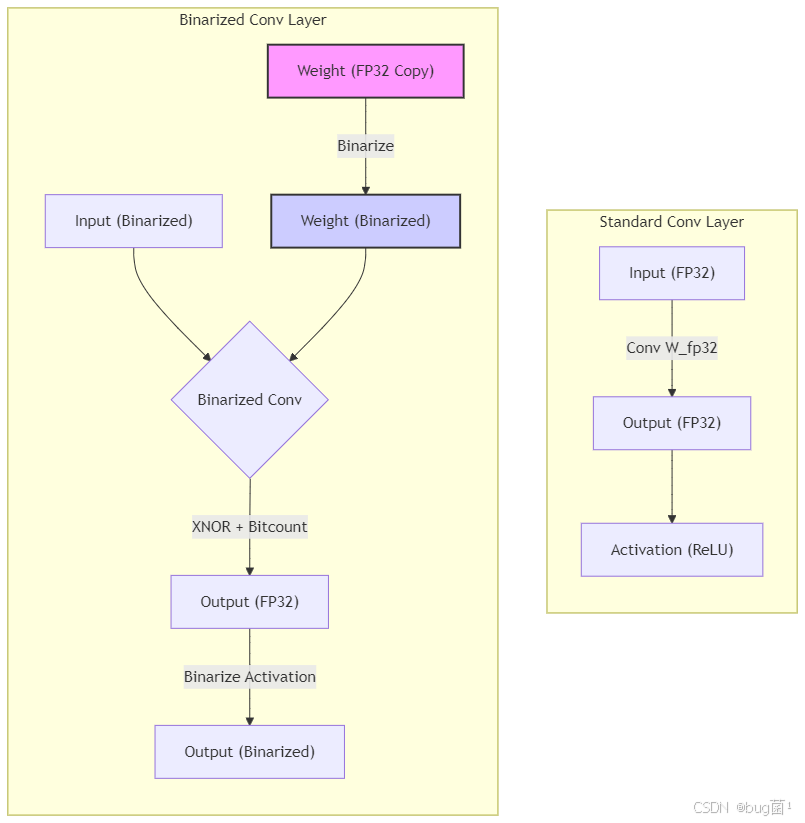
图解：在一个二值化卷积层中，输入的激活值和层的权重都是 +1-1 的形式。计算过程不再是乘加，而是高效的位运算。计算得到的输出在送入下一层之前，会再次经过一次二值化。注意图中那个粉色的 Weight (FP32 Copy)，这是训练BNN的关键，我们稍后会详细解释。

2.3 性能的飞跃：从乘法到异或门

  为什么说二值化能带来计算效率的飞跃？让我们来看一个简单的向量点积的例子。假设我们有两个向量 $\mathbf{a}$ 和 $\mathbf{w}$：

• 标准情况 (FP32)：$\mathbf{a}=[0.8,-1.2,0.3]$, $\mathbf{w}=[0.6,2.1,-1.5]$

  计算点积需要进行3次浮点乘法和2次浮点加法：

$$(0.8\times 0.6)+(-1.2\times 2.1)+(0.3\times -1.5)=48-2.52-0.45=-2.49$$

• 二值化情况 (BNN)：${\mathbf{a}}_b=[+1,-1,+1]$, ${\mathbf{w}}_b=[+1,+1,-1]$

  由于 $a\times w$ 的结果只可能是 +1 (当符号相同时) 或 -1 (当符号不同时)，这与 NOT(a XNOR w) 的逻辑是等价的（如果我们将+1映射为1，-1映射为0）。

• +1 * +1 = +1 (符号相同)
• -1 * -1 = +1 (符号相同)
• +1 * -1 = -1 (符号不同)
• -1 * +1 = 1 (符号不同)

  这个乘法过程可以完全用位运算XNOR替代。而后续的累加过程，则变成了统计+1的数量，这可以通过硬件上的popcount或bitcount指令高效完成。这使得BNN在能耗和速度上，尤其是在定制硬件上，具有无与伦比的优势。

⏩ 3. 权重与激活的二值化策略

  理论听起来很美妙，但具体如何实现呢？我们来看看权重和激活是如何从全精度“变身”为1-bit的。

3.1 权重的二值化：如何保留“灵魂”信息

3.1.1 确定性二值化：Sign函数

  最直观、最常用的二值化方法是使用符号函数（Sign function）。
  对于任意一个全精度（real-valued）的权重 $w_r$，其二值化后的权重 $w_b$ 定义为：

$$w_b=\text{Sign}(w_r)=\{\begin{array}{ll}+1,& \text{if }{w}_r\ge 0\\ -1,& \text{if }{w}_r<0\end{array}$$

  这个函数非常简单：所有正数（包括 0）都变成 +1，所有负数都变成 -1。

3.1.2 关键的尺度因子 $\alpha$

  然而，仅仅使用 Sign 函数会丢失一个至关重要的信息：原始权重矩阵的尺度（magnitude）。
比如，一个权重矩阵 [0.1, 0.2] 和另一个 [10, 20]，它们二值化后都变成了 [+1, +1]，但它们的能量和对输出的影响显然是完全不同的。

  为了弥补这个损失，XNOR-Net 等开创性工作引入了一个 尺度因子 $\alpha$。
二值化的过程被修正为：

$$W_b=\alpha B=\alpha \cdot \text{Sign}(W_r)$$

  其中，$W_r$ 是全精度的权重张量，$B$ 是通过 Sign 函数得到的二值张量，而 $\alpha$ 是一个正的标量。

  这个 $\alpha$ 怎么计算呢？最常见的方式是取原始权重绝对值的平均值：

$$\alpha =\frac{1}{n}\sum _{i=1}^n|W_{r_i}|=\frac{\Vert W_r{\Vert }_{L1}}{n}$$

  这里 $n$ 是权重张量中元素的总数。

  这个尺度因子 $\alpha$ 相当于保留了原始权重矩阵的“平均能量”，它会在前向传播时乘以二值化卷积的结果，从而使得输出的尺度更接近于全精度网络的输出。

3.2 激活的二值化：信息流的“开关”

  与权重类似，激活值也需要被二值化。
  通常，激活二值化发生在卷积或全连接层之后、非线性激活函数（如 ReLU）之前或之后。
  最简单的方式同样是使用 Sign 函数：

$$a_b=\text{Sign}(a_r)$$

  但这里需要注意，通常我们会先对卷积层的输出进行 BatchNorm（批归一化），然后再进行二值化。
  这样做有助于稳定训练过程，使得输入到 Sign 函数的数据分布更加规整。

⏩ 4. 训练的艺术：梯度反向传播的“断崖”

4.1 梯度消失的困境：Sign函数的“无情”

  我们已经设计好了前向传播，但神经网络的灵魂在于 反向传播和梯度下降。
  这里，BNN 遇到了一个致命的问题。

  回顾一下 Sign 函数的形状，它是一个阶跃函数。
  它的导数（梯度）在除了零点之外的所有地方都为 0：

$$\frac{d}{dx}\text{Sign}(x)=\{\begin{array}{ll}0,& x\ne 0\\ \text{undefined},& x=0\end{array}$$

  这意味着，在反向传播过程中，当梯度流经一个 Sign 函数时，它会直接乘以 0，然后消失得无影无踪。 整个网络将无法学习，因为参数收不到任何有效的梯度更新信号。

  这就像是在一个完全平坦的高原上寻找下山的路 —— 你根本不知道该往哪个方向走。

4.2 “偷天换日”：直通估计器（Straight-Through Estimator, STE）

  为了解决这个“梯度断崖”问题，研究者们提出了一种非常巧妙、堪称“魔法”的近似方法——直通估计器（Straight-Through Estimator, STE）。

  STE 的核心思想是：在前向传播时，我们使用非线性的、不可导的二值化函数（如 Sign）；但在反向传播时，我们“假装”这个函数的导数是一个表现良好的函数，直接让梯度“通过”。

  具体来说，对于 Sign 函数，我们在反向传播时，假设它的导数恒为 1。
也就是说，如果我们有一个损失函数 $L$，和二值化后的权重 $w_b=\text{Sign}(w_r)$，则梯度近似为：

$$\frac{\partial L}{\partial w_r}=\frac{\partial L}{\partial w_b}\cdot \frac{\partial w_b}{\partial w_r}\approx \frac{\partial L}{\partial w_b}$$

  这样，上游传来的梯度 $\frac{\partial L}{\partial w_b}$ 就会被“复制”给 $w_r$。
STE 就好像一座桥梁，在梯度无法通过的断崖处，硬生生地架起了一条通路，让梯度信息能够顺畅地回传。

  此外，为了防止梯度过大导致训练不稳定，通常会增加一个“裁剪”操作。
当全精度权重的绝对值已经大于 1 时，就不再对其进行更新，因为它的符号已经很稳定了。
这可以用一个指示函数 1 { ∣ w r ∣ ≤ 1 } 1_{\{|w_r| \leq 1\}} 1{∣wr​∣≤1}​ 来表示：

∂ L ∂ w r    ≈    ∂ L ∂ w b ⋅ 1 { ∣ w r ∣ ≤ 1 } \frac{\partial L}{\partial w_r} \;\approx\; \frac{\partial L}{\partial w_b} \cdot 1_{\{|w_r| \leq 1\}} ∂wr​∂L​≈∂wb​∂L​⋅1{∣wr​∣≤1}​

4.3 STE工作原理图解

  我们可以用Mermaid图来清晰地展示STE是如何工作的：

图解：

• 蓝线（前向传播）：真实的全精度权重 $w_r$ 经过 Sign 函数，得到二值化的权重 $w_b$ 用于计算。
• 红虚线（反向传播）：损失函数对 $w_b$ 的梯度 $\frac{\partial L}{\partial w_b}$ 到达 STE 模块。
  STE “伪造”了一个梯度，直接传递给了 $w_r$，使得 $w_r$ 可以被正常更新。

  虽然 STE 在数学上不是严格的推导，但在实践中却取得了惊人的成功，使得训练 BNN 成为可能。

⏩ 5. 精度损失的救赎：提升BNN性能的实用技巧

  尽管BNN在理论上非常高效，但如此剧烈的信息压缩不可避免地会导致严重的精度下降。为了让BNN在像YOLOv8这样的复杂任务上表现得更好，研究者们总结了许多实用的技巧。

5.1 保持“精英”：首层与末层全精度处理

  一个被广泛采用的策略是不二值化网络的第一层和最后一层。

• 第一：输入图像通常包含丰富的颜色和细节信息。如果第一层就被二值化，会造成严重的信息瓶颈，后续网络很难恢复有用的特征。保持第一层为全精度，可以更好地提取底层特征。
• 最后一层：最后一层通常是分类器或回归头，需要输出精细的概率值或坐标值。对其进行二值化会严重限制模型的表达能力。

5.2 幕后英雄：保留全精度梯度副本

  这是训练BNN时一个至关重要的细节。二值化的权重 $w_b$ 只是在前向和反向传播计算梯度时使用的“临时工”。优化器（如Adam）在更新权重时，更新的是一个始终在后台维护的全精度权重副本 $w_r$。

  训练的流程如下：

1. 传播：将全精度权重 $w_r$ 二值化得到 $w_b$，然后用 $w_b$ 进行计算。
2. 反向传播：计算损失，梯度通过STE回传，得到对 $w_r$ 的梯度 $\frac{\partial L}{\partial w_r}$。
3. 权重更新：优化器使用梯度 $\frac{\partial L}{\partial w_r}$ 来更新全精度的 $w_r$。例如：$w_r\leftarrow w_r-\eta \frac{\partial L}{\partial w_r}$。

  这个全精度的 $w_r$ 就像一个“记忆体”，它不断累积微小的梯度更新，而它的符号（正或负）则决定了下一次前向传播时 $w_b$ 的值。

5.3 XNOR-Net：为激活也引入尺度因子

  类似于为权重引入尺度因子 $\alpha$，XNOR-Net 提出也为输入的 激活值 计算一个尺度因子 $\beta$。
这样，一个二值化的卷积操作可以近似为：

$$I\ast W\approx \beta H_b⊛(\alpha B)=(\alpha \beta )(H_b⊛B)$$

其中：

• $I,W$ ：全精度的输入与权重
• $H_b,B$ ：对应的二值化版本
• $⊛$ ：表示使用 XNOR 和 bitcount 实现的卷积操作

  因此，两个尺度因子 $\alpha$ 和 $\beta$ 的乘积能够更好地补偿二值化带来的尺度损失。

5.4 知识蒸馏的加持

  知识蒸馏是一种非常有效的提升BNN性能的方法。我们可以先训练一个全精度的YOLOv8模型作为“教师网络”，然后在训练二值化的YOLOv8（“学生网络”）时，不仅使用标准的检测损失，还额外增加一个蒸馏损失，让学生网络的输出去模仿教师网络的中间特征或最终输出。这为BNN的训练提供了更丰富的监督信号，能显著提升其最终精度。

⏩ 6. YOLOv8实战：构建并集成二值化卷积模块

  理论知识已经就绪，让我们开始动手编写代码吧！我们将实现一个BinarizedConv2d模块，它可以用来替换YOLOv8中的标准Conv2d。

6.1 核心组件：实现STE的二值化函数

  首先，我们需要创建一个自定义的PyTorch autograd.Function，它将在前向传播时执行二值化，并在反向传播时实现STE。

6.1.1 代码实现

相关示例代码演示如下，仅供参考：

import torch
import torch.nn as nn
from torch.autograd import Function

class BinarizeF(Function):
    """
    自定义的二值化PyTorch函数，包含STE用于反向传播
    """
    @staticmethod
    def forward(ctx, input):
        """
        前向传播：执行标准的Sign函数二值化
        """
        # 使用Sign函数将输入张量二值化为-1或1
        output = input.sign()
        return output

    @staticmethod
    def backward(ctx, grad_output):
        """
        反向传播：实现Straight-Through Estimator (STE)
        梯度直接“通过”，不经过Sign函数的导数计算
        """
        # grad_input = grad_output.clone()
        return grad_output

6.1.2 代码解析

• 我们创建了一个继承自torch.autograd.Function的类BinarizeF。这允许我们自定义前向和反向传播的行为。
• forward方法非常简单，就是对输入调用.sign()方法，得到+1-1的张量。ctx是上下文对象，可以用来存储一些值以便在反向传播时使用（这里我们没用到）。
• backward方法是STE的关键。它接收上游传来的梯度grad_output，并直接将其作为梯度的输出返回。这就实现了梯度的“直通”，绕过了Sign函数导数为0的问题。

6.2 BinarizedConv2d模块的完整实现

现在，我们利用上面的BinarizeF函数来构建一个完整的二值化卷积层。

6.2.1 代码实现

相关示例代码演示如下，仅供参考：

import torch.nn.functional as F

class BinarizedConv2d(nn.Conv2d):
    """
    一个实现了权重二值化的卷积层
    """
    def __init__(self, *kargs, **kwargs):
        super(BinarizedConv2d, self).__init__(*kargs, **kwargs)

    def forward(self, input):
        # ----------------- 权重二值化 -----------------
        # 1. 计算尺度因子 alpha (L1范数均值)
        #    注意：这里我们不在反向传播中计算alpha的梯度
        with torch.no_grad():
            scaling_factor = torch.mean(torch.mean(torch.mean(abs(self.weight),dim=3,keepdim=True),dim=2,keepdim=True),dim=1,keepdim=True)
        
        # 2. 对权重进行二值化
        #    注意：self.weight 是我们后台维护的全精度权重
        binarized_weight = BinarizeF.apply(self.weight)
        
        # 3. 为二值化权重应用尺度因子
        scaled_weight = binarized_weight * scaling_factor
        
        # ----------------- 卷积计算 -----------------
        # 使用带有缩放的二值化权重进行标准卷积
        # 注意：这里的输入input还没有被二值化，这是一个只对权重二值化的版本
        #      一个完整的BNN实现也会对input进行二值化
        output = F.conv2d(input,
                          scaled_weight,
                          self.bias,
                          self.stride,
                          self.padding,
                          self.dilation,
                          self.groups)
        return output

# --- 使用示例 ---
if __name__ == '__main__':
    # 创建一个随机输入张量
    x = torch.randn(1, 16, 32, 32) # (batch, channels, height, width)
    
    # 创建一个二值化卷积层
    b_conv = BinarizedConv2d(16, 32, kernel_size=3, padding=1) # (in_channels, out_channels, ...)
    
    print("全精度权重 (部分):", b_conv.weight.data.view(-1)[:5])
    
    # 执行前向传播
    y = b_conv(x)
    
    print("输出张量形状:", y.shape)
    
    # 模拟反向传播
    # 计算一个标量损失
    loss = y.sum()
    # 执行反向传播
    loss.backward()
    
    print("权重的梯度 (部分):", b_conv.weight.grad.view(-1)[:5])
    print("梯度成功通过STE回传!")

6.2.2 代码解析

1. 继承nn.Conv2d：我们的类继承自PyTorch的nn.Conv2d，这样我们可以复用其所有属性，如self.weight, self.bias, self.stride等。
2. 权重二值化流程：

• 计算尺度因子：scaling_factor = torch.mean(abs(self.weight), ...) 这行代码实现了我们之前讨论的 $\alpha =\frac{|W_r{|}_{L1}}{n}$。我们对权重的每个输出通道独立计算一个尺度因子。
• 二值化：binarized_weight = BinarizeF.apply(self.weight) 调用了我们之前定义的函数，self.weight是我们维护的全精度权重。
• 应用尺度：`scaled_weight = binarized_weight * scaling_factor乘回去。

3. 卷积计算：output = F.conv2d(...) 使用torch.nn.functional.conv2d函数执行卷积。关键是，我们传入的是scaled_weight，而不是原始的self.weight`。
4. 梯度：当loss.backward()被调用时，梯度会流经F.conv2d，然后到达scaled_weight。由于scaled_weight是由BinarizeF生成的，梯度会进入BinarizeF.backward方法，在那里，STE会确保梯度能够继续传递到self.weight，从而让我们的全精度权重得到更新。
5. 关于激活：请注意，在这个实现中，为了简化，我们只对权重进行了二值化。一个完整的BNN层（如XNOR-Net中的实现）会先对输入input也进行二值化（同样使用带STE的函数）。

6.3 如何在YOLOv8中集成BinarizedConv2d？

  将我们自定义的BinarizedConv2d模块集成到YOLOv8的框架中，需要一些“外科手术式”的操作，因为它涉及到修改YOLOv8的底层模型解析代码。不过别担心，我会一步步带你完成！💪

6.3.1 步骤一：定义新的BinarizedConv封装

  YOLOv8的Conv模块并不仅仅是一个nn.Conv2d，它通常还封装了批归批归一化（BatchNorm）和激活函数。为了无缝替换，我们也需要创建一个类似的封装，我们称之为BConv。

相关示例代码演示如下，仅供参考：

# 该代码片段可以和你之前的BinarizedConv2d放在同一个文件里
# 例如 ultralytics/nn/modules/conv.py

class BConv(nn.Module):
    """
    一个封装了BinarizedConv2d, BatchNorm和激活函数的模块，
    用于在YOLOv8的yaml文件中替换原有的'Conv'模块。
    """
    def __init__(self, c1, c2, k=1, s=1, p=None, g=1, d=1, act=True):
        super().__init__()
        # 使用我们自定义的二值化卷积层
        self.conv = BinarizedConv2d(c1, c2, k, s, p, g=g, d=d, bias=False)
        # 批归一化层在BNN中至关重要，它可以稳定训练
        self.bn = nn.BatchNorm2d(c2)
        # 激活函数。注意：在一个完整的BNN中，激活函数本身也会被一个
        # 二值化函数替代。这里为了简化集成，我们暂时保留标准的激活函数。
        self.act = nn.SiLU() if act is True else (act if isinstance(act, nn.Module) else nn.Identity())

    def forward(self, x):
        # 注意激活二值化的位置：
        # 一个完整的BNN实现，会在bn之后，act之前，对bn的输出进行二值化
        # x = BinarizeF.apply(x) # 激活二值化
        return self.act(self.bn(self.conv(x)))

    def forward_fuse(self, x):
        # 在fuse模式下（通常用于推理加速），BNN的融合逻辑会更复杂
        # 这里我们简单地返回标准的前向传播
        return self.act(self.bn(self.conv(x)))

6.3.2 步骤二：修改模型解析逻辑

  YOLOv8通过解析.yaml配置文件来构建模型。我们需要告诉它的解析器，当遇到我们新定义的BConv时该怎么做。

1. 解析器文件：
   这个文件通常在ultralytics/nn/tasks.py或者类似的模型构建脚本中，寻找一个名为parse_model的函数。

2. 导入新模块：
   在文件的开头，从你存放BConv模块的文件中导入它。

   # 在 ultralytics/nn/tasks.py 的开头
   from ultralytics.nn.modules import BConv, Conv, ... # 假设你把BConv放在了modules/__init__.py或conv.py中
   

3. 让解析器识别BConv：
   在parse_model函数内部，你会找到一个很长的if-lif语句块，它根据m（模块名）来创建不同的层。你只需要找到处理Conv的地方，把`BConv加进去。

   # 在 parse_model 函数内部
   ...
   # 原来的代码可能长这样:
   # if m in (Conv, ConvTranspose, GhostConv, Bottleneck, GhostBottleneck, ...):
   #     c1, c2 = ch[f], args[0]
   #     args = [c1, c2, *args[1:]]
   
   # 你需要把它修改成这样，让 BConv 和 Conv 使用相同的参数解析逻辑：
   if m in (BConv, Conv, ConvTranspose, GhostConv, Bottleneck, GhostBottleneck, ...):
       c1, c2 = ch[f], args[0]
       args = [c1, c2, *args[1:]]
   ...
   

4. 创建并使用新的.yaml文件：

  现在，你可以复制一份例如yolov8n.yaml的文件，重命名为yolov8n-bnn.yaml。在文件中，你可以选择性地将一些Conv模块替换为BConv。

# yolov8n-bnn.yaml (部分示例)

# ... 省略前面的部分

backbone:
  # [from, repeats, module, args]
  - [-1, 1, Conv, [64, 3, 2]]  # P1/2  -- 保持第一层为全精度
  - [-1, 1, BConv, [128, 3, 2]] # P2/4  -- 使用二值化卷积
  - [-1, 3, C2f, [128, True]]
  - [-1, 1, BConv, [256, 3, 2]] # P3/8  -- 使用二值化卷积
  - [-1, 6, C2f, [256, True]]
  - [-1, 1, BConv, [512, 3, 2]] # P4/16 -- 使用二值化卷积
  - [-1, 6, C2f, [512, True]]
  - [-1, 1, BConv, [1024, 3, 2]] # P5/32-- 使用二值化卷积
  - [-1, 3, C2f, [1024, True]]
  - [-1, 1, SPPF, [1024, 5]]

# ... head部分类似修改，但建议保持最后的检测头为全精度

head:
  # ...
  - [[-1, -2, -3], 1, Concat, [1]]
  # ...
  - [-1, 3, C2f, [1024]]
  - [-1, 1, Conv, [256, 1, 1]] # 保持检测头附近为全精度

6.3.3 训练的挑战与建议

重要提示：训练BNN比训练全精度模型要困难得多，你需要有足够的耐心和技巧！❤️

1. 优化器选择：Adam优化器通常比SGD更适合训练BNN，因为它对每个参数使用自适应学习率，有助于处理BNN训练中不稳定的梯度。
2. 学习率策略：使用一个较小的初始学习率，并配合余弦退火（Cosine Annealing）等学习率调度器。BNN的权重空间非常崎岖，平缓的学习率下降有助于模型找到一个较好的局部最优解。
3. 激活二值化：我们上面的例子只二值化了权重。要实现一个完整的BNN，你还需要在BConv的forward函数中，对输入x进行二值化（通常在BatchNorm之后）。
4. 分阶段训练：一个非常有效的策略是，先加载一个预训练的全精度YOLOv8模型，然后用你的yolov8n-bnn.yaml配置文件构建一个二值化模型，并将全精度模型的权重加载到BNN模型中（PyTorch会自动匹配层名）。然后，在这个基础上进行微调（fine-tuning）。这为BNN提供了一个非常好的初始化状态。
5. 耐心，耐心，再耐心：BNN的收敛速度可能更慢，精度可能会有明显下降。不要期望它能轻松达到全精度模型的水平。它的主要优势在于部署时的极致效率。

⏩ 7. 总结与展望

  恭喜你坚持到了最后！你已经完成了对极限压缩技术——二值神经网络（BNN）的深度探索！👍

  在今天的旅程中，我们从BNN的核心思想出发，理解了它为何能带来 32倍的模型压缩 和 飞的计算效率提升。我们深入剖析了其两大基石——权重与激活的二值化策略，并揭示了解决梯度消失问题的“黑魔法”—— 直通估计器（STE）。我们还学习了多种提升BNN性能的实用技巧，如保留首末层全精度、使用尺度因子等。

  最激动人心的是，我们亲手编写了BinarizedConv2d的核心代码，并详细探讨了如何一步步将其集成到强大的YOLOv8框架中。这不仅仅是理论学习，更是通往实践应用的桥梁。

  BNN代表了模型轻量化的一个极端方向，它用精度上的牺牲换取了在资源极度受限设备上运行的可能性。虽然它可能不会在所有场景下都取代全精度模型，但它为边缘计算、物联网、移动设备等领域打开了一扇全新的大门。掌握BNN，意味着你拥有了一项能将复杂模型部署到更多角落的强大武器！💖

⏩ 8. 下期预告：Knowledge Distillation卷积知识蒸馏

  在探索了稀疏化、二值化等各种“压榨”模型自身潜力的技术后，我们不禁会问：有没有办法让模型“向外学习”，借助更强大的模型的智慧来提升自己呢？

  答案是肯定的！这就是我们下一节的主题—— 知识蒸馏（Knowledge Distillation）。

  这项技术就像一位经验丰富的老师傅（教师网络）手把手地教导一个新手学徒（学生网络）。通过让学生网络去模仿教师网络的行为，我们可以将一个庞大、复杂但性能优越的模型的“知识”提炼并“蒸馏”到一个轻量级的模型中。

  这对于我们刚刚讨论的BNN等压缩模型来说，简直是天作之合！知识蒸馏是弥补量化、二值化等技术带来的精度损失最有效的手段之一。

• 一个庞大的YOLOv8x模型，如何将其检测的“精髓”传授给一个轻量级的YOLOv8n？
• 除了模仿最终的输出，我们还能从教师网络的“思考过程”（中间特征图）中学到什么？
• 如何设计巧妙的蒸馏损失函数，来平衡学生自身的学习和向老师的学习？

  在下一节 《YOLOv8【卷积创新篇·第2】Knowledge Distillation卷积知识蒸馏》 中，我们将深入探索知识蒸馏的奥秘，学习如何让你的轻量级模型站在“巨人”的肩膀上，实现性能的再次飞跃！敬请期待，我们下期再见！✨✨✨

---

  希望本文所提供的YOLOv8内容能够帮助到你，特别是在模型精度提升和推理速度优化方面。

  PS：如果你在按照本文提供的方法进行YOLOv8优化后，依然遇到问题，请不要急躁或抱怨！YOLOv8作为一个高度复杂的目标检测框架，其优化过程涉及硬件、数据集、训练参数等多方面因素。如果你在应用过程中遇到新的Bug或未解决的问题，欢迎将其粘贴到评论区，我们可以一起分析、探讨解决方案。如果你有新的优化思路，也欢迎分享给大家，互相学习，共同进步！

🧧🧧 文末福利，等你来拿！🧧🧧

  文中讨论的技术问题大部分来源于我在YOLOv8项目开发中的亲身经历，也有部分来自网络及读者提供的案例。如果文中内容涉及版权问题，请及时告知，我会立即修改或删除。同时，部分解答思路和步骤来自全网社区及人工智能问答平台，若未能帮助到你，还请谅解！YOLOv8模型的优化过程复杂多变，遇到不同的环境、数据集或任务时，解决方案也各不相同。如果你有更优的解决方案，欢迎在评论区分享，撰写教程与方案，帮助更多开发者提升YOLOv8应用的精度与效率！

  OK，以上就是我这期关于YOLOv8优化的解决方案，如果你还想深入了解更多YOLOv8相关的优化策略与技巧，欢迎查看我专门收集YOLOv8及其他目标检测技术的专栏《YOLOv8实战：从入门到深度优化》。希望我的分享能帮你解决在YOLOv8应用中的难题，提升你的技术水平。下期再见！

  码字不易，如果这篇文章对你有所帮助，帮忙给我来个一键三连（关注、点赞、收藏），你的支持是我持续创作的最大动力。

  同时也推荐大家关注我的公众号：「猿圈奇妙屋」，第一时间获取更多YOLOv8优化内容及技术资源，包括目标检测相关的最新优化方案、BAT大厂面试题、技术书籍、工具等，期待与你一起学习，共同进步！

🫵 Who am I?

我是bug菌，CSDN | 掘金 | InfoQ | 51CTO | 华为云 | 阿里云 | 腾讯云 等社区博客专家，C站博客之星Top30，华为云多年度十佳博主，掘金多年度人气作者Top40，掘金等各大社区平台签约作者，51CTO年度博主Top12，掘金/InfoQ/51CTO等社区优质创作者；全网粉丝合计 30w+；更多精彩福利点击这里；硬核微信公众号「猿圈奇妙屋」，欢迎你的加入！免费白嫖最新BAT互联网公司面试真题、4000G PDF电子书籍、简历模板等海量资料，你想要的我都有，关键是你不来拿。

-End-