从策略梯度到近端策略优化

在强化学习领域，PPO (Proximal Policy Optimization) 算法无疑是很优秀的。它以其出色的稳定性、易于实现和卓越的性能，成为了许多研究和应用的首选算法。

但PPO并非横空出世，它是站在巨人肩膀上的产物。要真正理解PPO为什么这么有效，我们必须沿着它的进化路径，从最基础的策略梯度 (Policy Gradient) 讲起，途经 Actor-Critic、TRPO，最终才能领会PPO设计的精妙之处。

一、 什么是强化学习？(基础知识)

在深入PPO之前，我们必须先理解强化学习 (Reinforcement Learning, RL) 的基本框架。

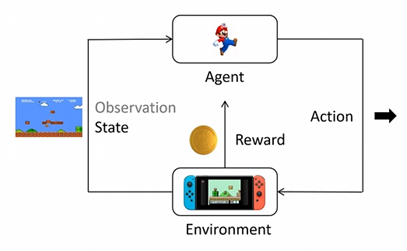
想象一个智能体 (Agent)（比如一个游戏角色或机器人）在一个环境 (Environment) 中（比如一个游戏关卡或现实世界）。这个过程是这样循环的：

1. 状态 (State)：智能体首先观察环境，获得一个状态 (State) 或观察 (Observation)。

2. 动作 (Action)：基于这个状态，智能体从它所有可能的“动作空间” (Action Space) 中（例如“向左”、“向右”、“跳跃”），选择一个动作 (Action) 来执行。

3. 奖励 (Reward)：环境接收到这个动作后，会给智能体一个奖励 (Reward)（可能是正分，也可能是负分），并进入下一个状态。

智能体做决策的“大脑”被称为策略 (Policy)，通常用 表示。策略是一个函数，它输入当前的状态，然后输出一个概率分布，决定采取每个动作的可能性。例如，π(向左|)=0.1, π(向右|)=0.7。

智能体与环境互动的一整串序列 {,,,,...} 被称为一条轨迹 (Trajectory)。从某个时间点到游戏结束的所有奖励总和，被称为回报 (Return)。

强化学习的最终目标就是：训练这个策略网络 ，使其在所有可能的轨迹中，获得的期望回报最大化 。

这个智能体一般是一个深度神经网络

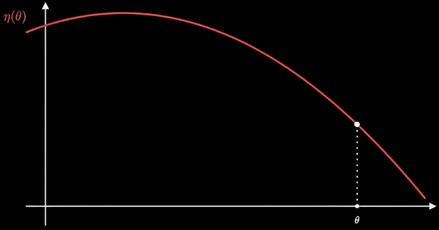
将这个神经网络的所有权重拿出来可以拍成一个高维向量,如果将其放在一个数轴上，就是一个点，对此时的网络性能打分就是,让它动起来就形成了目标函数曲线。训练的目的就是找到顶点，也就是最优参数。

这个目标函数曲线写成迭代式子为：

这个公式的核心就是： 新策略的回报 = 旧策略的回报 + “在新策略的状态分布下，执行新策略动作所能带来的（相对于旧策略的）优势总和”

二、 策略梯度 (PG)：让回报“飞一会儿”

当前对下一步新策略和状态分布都不可知，就好像一个人孤零零的站在一根柱子上，不知道哪边是上山，哪边是下山。

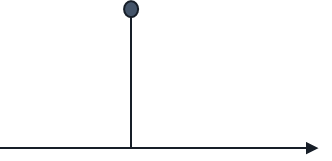
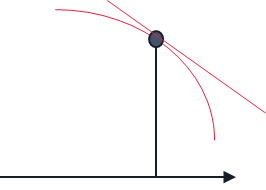
怎么走才能快速达到山顶？也就是如何快速到达最大值。

常见的方法就是沿切线向上。

策略梯度 (Policy Gradient, PG) 是最直接的想法。想象一个目标函数 ，它代表了策略 的期望回报。我们如何最大化它？

答案是：梯度上升。就像爬山一样，我们只需要沿着梯度的方向（最陡峭的方向）更新策略参数 即可 。

通过一系列推导，我们得到了PG的梯度估计器 ：

这里的 一开始是指 时刻之后的总回报 。这个公式的直观理解是：

• 如果在 之后获得了高回报（为正且大），我们就增大 ，即增加在 状态下执行 动作的概率。

• 反之，如果回报低，就降低这个概率。

所以这样就完成了对“在新策略的状态分布下，执行新策略动作所能带来的（相对于旧策略的）优势总和”的估计。

但这有个大问题：方差太高 。 是一个随机采样值，波动极大，导致训练过程非常不稳定。

三、 升级：从PG到Actor-Critic (A2C) 和 GAE

为了解决高方差问题，研究者们引入了两个关键技术：Actor-Critic 和 GAE。

1. Actor-Critic (A2C)

对上述公式继续推导：

第一个推导 (Line 1 -> Line 2)：使用“未来回报”

Line 1:

Line 2:

1. 符号解释：

• ：这是第 n 条完整轨迹 (Trajectory) 的总回报 (Total Return)。

  （即从头到尾所有奖励的总和）。

• ：这是从 t 时刻开始的未来回报 (Future Return)，也叫 "Return-to-Go"。

  （即从 t 时刻到回合结束的奖励总和）。

2. 为什么可以这么做：

强化学习中有一个基本原则：“在 t 时刻做出的动作 a_t，只会影响 t 时刻及之后获得的奖励，无法影响 t 时刻之前已经获得的奖励。”

• Line 1 的问题： 它使用总回报 来评估在 t 时刻的动作 a_n^t。

  包含了两部分：

  1. 过去的奖励：

  2. 未来的奖励： (这正是 )

• 用一个包含了“过去奖励”的值来评估“当前动作”的好坏，显然是不合理的。这个“过去的奖励”就像一个“噪音”，它与 的好坏无关，但会使 的值波动很大（即高方差）。

• Line 2 的改进： 我们只使用未来回报 来评估 。这更公平，更准确，因为它只包含了 真正能影响到的那部分奖励。

第二个推导 (Line 2 \rightarrow Line 3)：引入“基线”

Line 2:

Line 3:

1. 符号解释：

• ：一个基线 (Baseline) 函数。这是一个只和状态 有关，而和动作 无关的函数。

• 最常用的基线就是状态价值函数 (Value Function) ，它表示“在状态 下，平均能获得多少未来回报”。

2. 推导的直觉（为什么可以这么做）：

• Line 2 的问题： 假设在一个游戏中，无论你做什么动作，你得到的未来回报 总是正的（比如总是在 [100, 120] 之间）。

  • 如果你做了一个“很差”的动作，得了 100 分 ( = 100)。

  • 如果你做了一个“很好”的动作，得了 120 分 ( = 120)。

  • 按照 Line 2 的公式， 永远是正的（因为 > 0）。这意味着算法会增加所有动作的概率，包括那个“很差”的动作。这显然不是我们想要的。

• Line 3 的改进： 我们引入一个“平均分”基线 （比如 ）。我们用优势 (Advantage) 来评估动作：

  • “很差”的动作：  = 100 - 110 = -10。梯度项 为负，算法会降低这个动作的概率。

  • “很好”的动作： = 120 - 110 = +10。梯度项 为正，算法会增加这个动作的概率。

通过减去一个基线，我们将“奖励”从“绝对的好坏”变成了“相对的好坏”（即比平均好还是比平均差），这使得学习信号更清晰，方差更小。

这就是 REINFORCE with Baseline 算法的核心，也是 A2C (Actor-Critic) 算法的基石。

我们训练两个网络 ：

1. Actor (演员): 策略网络 ，负责做动作。

2. Critic (评论家): 价值网络 ，负责评估当前状态 的“平均价值” 。

然后，我们定义优势函数 (Advantage Function) ：

它衡量的是：在状态 下，执行动作 相比于“平均水平” 到底有多好。用 替换 可以显著降低方差。

2. GAE (Generalized Advantage Estimation)

那怎么估计 呢？

定义如下函数：其中是衰减系数

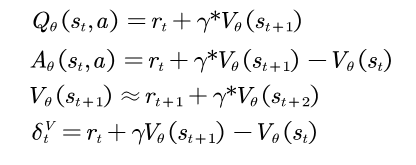
我们又面临一个偏差-方差权衡：

• 1-步TD估计：。这其实就是 TD 误差  。它偏差高（因为依赖 的估计），但方差低。

• 蒙特卡洛估计：。它偏差低（全用真实奖励），但方差高。

GAE 的核心思想是不只选择其中一种，而是将所有 n-步 优势估计值 进行一次“加权平均”。

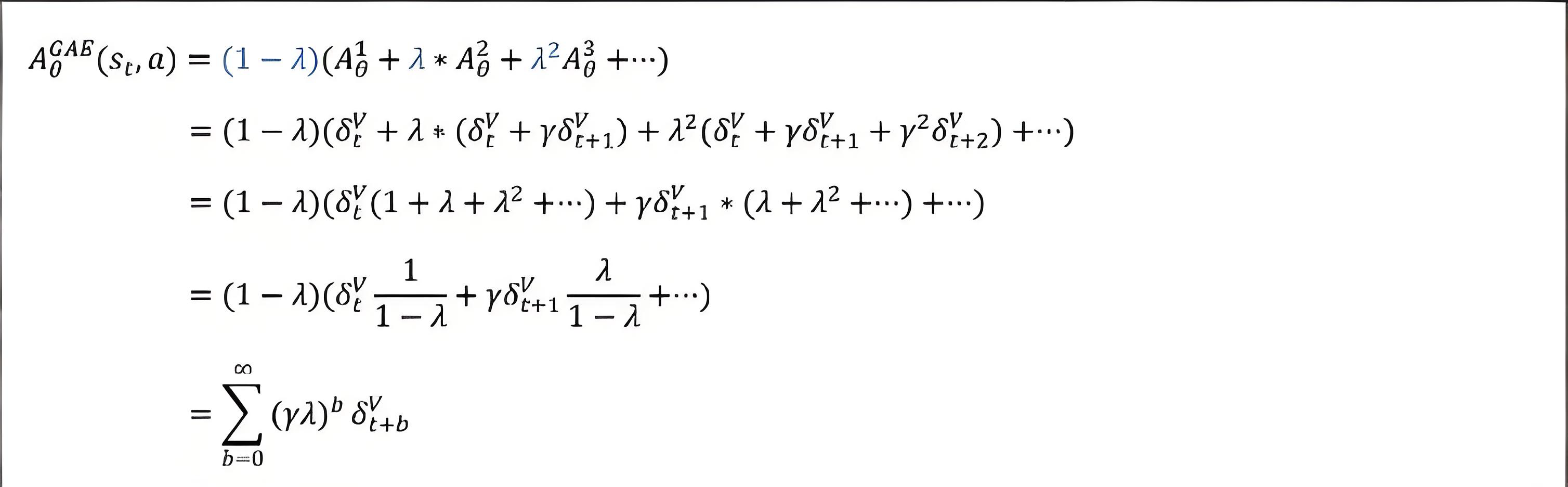
此时，期望回报函数用上述估计变为：

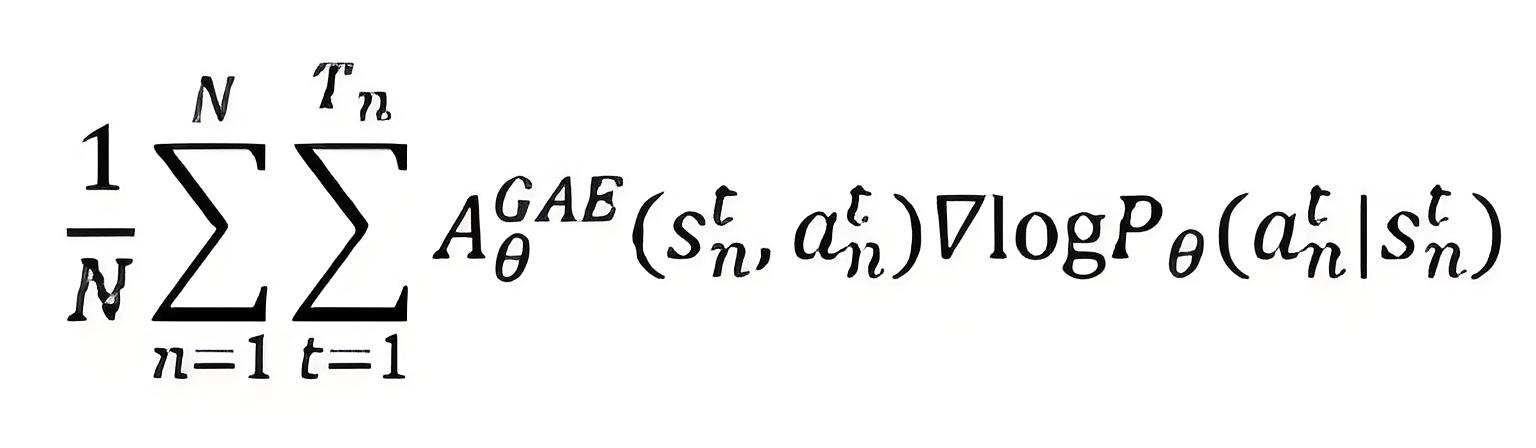
四、 效率革命：从 On-Policy 到 Off-Policy (TRPO)

TRPO (Trust Region Policy Optimization)

策略梯度存在的问题：为了安全起见，每次向上只走α一小步，移动速度会很慢

TRPO创造性的提出的一条安全线：

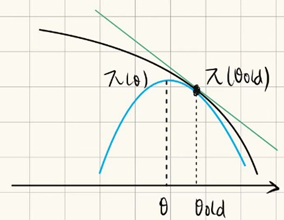
通过寻找新函数的最大值（蓝线顶点），就能更快的更新策略

所用的A2C + GAE 已经很好了，但还有个效率问题：它们是 On-Policy 的。这意味着 Actor 采样回来的数据 (Trajectory) 只能用来更新一次，更新完就必须丢弃，再用新策略去采样。这非常浪费！

重要性采样 (Importance Sampling)

为了重用数据 (Off-Policy)，我们引入重要性采样 (Importance Sampling) 。

目标分布 p(x)： 就是我们想要优化的新策略

采样分布 q(x)： 就是我们刚刚用来收集数据的旧策略

我们想用旧策略 采到的数据，来评估新策略 。这需要乘以一个概率比率 ：

此时，我们的目标函数变成了：

 但  可能是个“炸弹”。如果新旧策略差异太大，这个比率会变得非常大或非常小，导致更新极其不稳定。TRPO (Trust Region Policy Optimization)对其进行限制：

这个限制就形成了一个区域，而这个区域就是所说的信赖域(Trust Region)，如图：

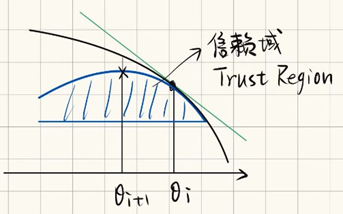
可以理解为在这个区域内是绝对安全的，现在就变成了寻找这个区域的顶点

此时上述所说的都是梯度策略的切线，对进行重要性采样，

对于此时的可以理解为在当前有策略，往前瞄准某个新策略，扔一个钩子进行瞄定，然后在当前点和锚点之间拉一条悬索，此时不再是切线，而是一条微弯的曲线，但起到的作用还是一样的，是为探索所构建的临时性安全保护措施。

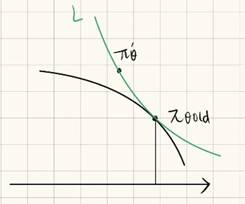
简单来说，TRPO算法就重复以下两个步骤(1.近似，2.最大化)：

五、 PPO登场：TRPO的“简易版”

TRPO 的效果非常好，但它的 KL 约束是一个带约束的优化问题，在计算上非常复杂，需要用到复杂的二阶优化方法，难以实现 。

PPO (Proximal Policy Optimization)  的目标是：在实现 TRPO 稳定性的同时，只使用简单的一阶梯度方法。

PPO-Clip

PPO 最核心的创新是 PPO-Clip ，它把 TRPO 的“硬约束”巧妙地转化为了一个“软裁剪”的目标函数。

请看这个 PPO 的核心公式：

它是如何工作的？

这里的 是一个超参数（比如0.2）。 函数会把 强行限制在 这个小区间内（例如 ）。

我们来分析 函数里的两项：

1. ：这是原始的 CPI 目标。

2. ：这是“裁剪后”的目标。

PPO 通过取这两项的最小值，达到了 TRPO 的效果：

• Case 1: （这是个好动作）

  • 此时，我们希望增大 (让 更倾向于做这个动作)。

  • 但 的 函数会给施加一个“天花板”。当 增大到 之后， 这一项就不再增大了。

  • 因此， 函数会取 这一项，即 。

  • 结果：目标函数不再增长，梯度消失。这阻止了策略更新幅度过大。

• Case 2: （这是个坏动作）

  • 此时，我们希望减小 (让 减少做这个动作)。

  • 当 减小到 之后， 这一项就不再减小了（因为 是负的）。

  • 函数会取 这一项，即 。

  • 结果：目标函数不再下降。这阻止了策略更新幅度过大。

PPO-Penalty

在优化理论层面，也可以将这种约束作为惩罚项。这是 PPO 提出的另一种形式，它不使用“硬截断”，而是使用“KL 散度”作为惩罚项（Penalty）来“软约束”策略的更新。

• 是新旧策略之间的 KL 散度，用于衡量两个策略的“距离”。

• 是一个惩罚系数（超参数），它平衡了“提升回报”和“保持接近”这两个目标。

在PPO论文中，这个 还会根据实际的 KL 散度与目标 KL 散度的差距进行自适应调整（Adaptive KL Penalty）。

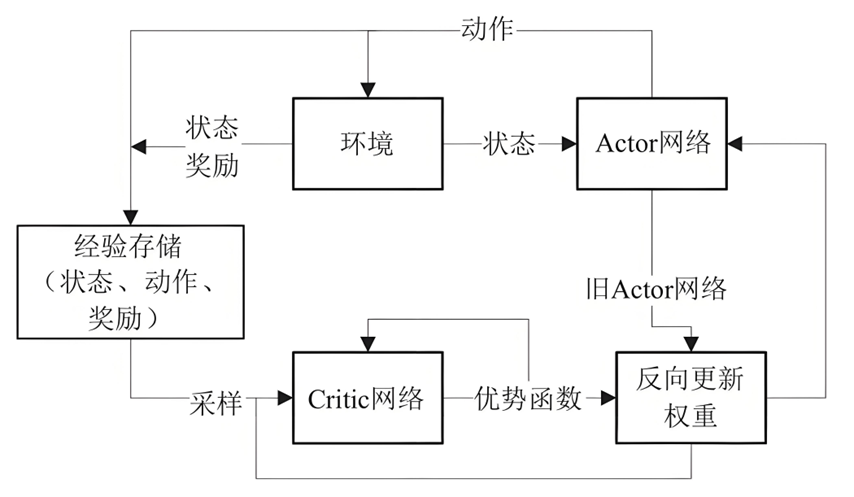
PPO算法流程图：

总结

PPO-Clip 通过一个简单的 min 和 clip 操作，移除了策略过度更新的动机，将策略更新限制在一个隐形的“信赖域”内，同时它又是一个普通的目标函数，可以轻松地用 Adam 等一阶优化器进行优化。PPO 算法的整体流程是：Actor 与环境交互，收集数据 ，然后 Critic 计算优势函数（用GAE），最后 Actor 使用 目标函数进行多次迭代更新。