强化学习(1)基础理论
作为初学者,首先我们来了解一些基础概念,我并且会给一个例子来感受强化学习,例子中用的是
gym库
强化学习(RL)核心概念总结
强化学习(Reinforcement Learning, RL)是一种独特的机器学习范式,它让智能体(Agent)通过与环境(Environment)的不断交互来学习最优行为,以最大化其获得的累积奖励(Return)
一、基本组成要素(The Main Characters)
| 名词 | 英文 | 解释 |
|---|---|---|
| 智能体 | Agent | 决策者和学习者。它感知状态,选择并执行动作。 |
| 环境 | Environment | 智能体所处的外部世界。它对智能体的动作做出反应,并给出奖励和新状态。 |
| 状态 | State (SSS) | 环境在某一时刻的描述,是智能体做出决策的依据。 |
| 动作 | Action (AAA) | 智能体在某一状态下可以做出的选择或行为。 |
| 奖励 | Reward (RRR) | 环境对智能体动作的即时反馈(正向或负向)。智能体的目标是最大化长期的累积奖励。 |
| 策略 | Policy (π\piπ) | 智能体的行为规则,是从状态到动作的映射(即在特定状态下应该做什么)。 |
| 回合 | Episode | 智能体从初始状态开始,到终止状态(如游戏结束)为止的完整交互序列。 |
| 轨迹 | Trajectory | 智能体与环境交互的历史记录序列:S0,A0,R1,S1,A1,R2,S2,…S_0, A_0, R_1, S_1, A_1, R_2, S_2, \dotsS0,A0,R1,S1,A1,R2,S2,… |
随机性体现在两点
- 动作的随机性,他依赖于策略π\piπ
- 状态的随机性,他依赖于状态转移函数
二、长期回报与评估(Long-Term Value and Evaluation)
强化学习的核心在于最大化长期回报,而非即时奖励(可不是贪心)
| 名词 | 英文 | 解释 |
|---|---|---|
| 折扣因子 | Discount Factor (γ\gammaγ) | 衡量未来奖励相对当前奖励的价值(0≤γ≤10 \le \gamma \le 10≤γ≤1)。γ\gammaγ 越接近 111,智能体越看重长期回报。 |
| 回报/累积奖励 | Return (GGG) | 从某一时间步开始,未来所有奖励的折扣总和。这是智能体试图最大化的目标。 |
| 状态价值函数 | State-Value Function (Vπ(s)V^\pi(s)Vπ(s)) | 在策略 π\piπ 下,从状态 sss 开始,预期能获得的累积折扣奖励。它评估了一个状态的长期“好坏”。 |
| 动作价值函数 | Action-Value Function (Qπ(s,a)Q^\pi(s, a)Qπ(s,a)) | 在策略 π\piπ 下,在状态 sss 采取动作 aaa 后,预期能获得的累积折扣奖励。它评估了在特定状态下,采取某个动作的长期“好坏”。 |
对于Return(G)Return(G)Return(G)来说,他依赖于ttt时刻,以及未来时刻的奖励,因此为了可以了解到GGG的大小,我们会对他进行求期望,从而排除掉其中的随机性(行为与状态),这里我们将消除随机性,指的是消除了未来的随机性,使得GGG只依赖于当下的行为与状态
计算期望之后,那么GGG其中只会留下St=stS_t=s_tSt=st以及At=atA_t=a_tAt=at这两个变量,通过求期望,我们得到了Qπ(st,at)Q^\pi(s_t,a_t)Qπ(st,at)函数,因此动作价值函数此时依赖π,st,at\pi,s_t,a_tπ,st,at,为了消除π\piπ,那么我们针对π\piπ进行求maxmaxmax
Q∗(st,at)=maxπQπ(st,at)Q^*(s_t,a_t)=max_\pi{Q^\pi(s_t,a_t)}Q∗(st,at)=maxπQπ(st,at)
其中的Q∗Q^*Q∗就是最优动作价值函数,他只依赖于st,ats_t,a_tst,at,与π\piπ无关
三、核心数学框架与方法(The Formal Framework)
| 名词 | 英文 | 解释 |
|---|---|---|
| 马尔可夫决策过程 | Markov Decision Process (MDP) | 强化学习的数学框架。它要求环境具有马尔可夫性(即下一状态仅取决于当前状态和动作)。 |
| 贝尔曼方程 | Bellman Equation | 将价值函数分解为即时奖励和下一状态的折扣价值的递归关系式,是计算和更新价值函数的基础。 |
| 探索与利用 | Exploration vs. Exploitation | 探索:尝试新的动作以发现潜在的更好奖励。利用:选择当前已知能带来最大预期奖励的动作。智能体必须权衡两者。 |
| 有模型学习 | Model-Based RL | 算法试图学习环境的模型(即预测下一个状态和奖励),然后用模型进行规划来优化策略。 |
| 无模型学习 | Model-Free RL | 算法不学习环境的模型,而是直接通过与环境的试错交互来学习策略或价值函数。 |
在深入学习具体的算法(如 Q-Learning、SARSA、Policy Gradient 等)时,会发现它们都是围绕着如何估计和优化这些价值函数和策略而展开的。

因此RL的流程可以简单如下,根据初始环境状态StS_tSt,Agent做出行为ata_tat,以此产生奖励rtr_trt,然后状态从StS_tSt到St+1S_{t+1}St+1,依此类推,这个过程Agent始终是为了获得未来尽量多的奖励
经典游戏CartPole
import gymnasium as gym
import numpy as np
import time
# 1. 初始化环境和参数
# CartPole-v1是一个经典环境
# 不仅仅要安装gymnasium库,也需要gymnasium[classic-control]
env = gym.make("CartPole-v1")
# Q-Learning 超参数
LEARNING_RATE = 0.1 # 学习率 (Alpha)
DISCOUNT = 0.95 # 折扣因子 (Gamma)
EPISODES = 20000 # 训练回合数
# 探索与利用参数
epsilon = 1.0 # 初始探索率
START_EPSILON_DECAY = 1 # 开始衰减的回合
END_EPSILON_DECAY = EPISODES // 2 # 探索率衰减到最小的回合
epsilon_decay_value = epsilon / (END_EPSILON_DECAY - START_EPSILON_DECAY)
# 2. 状态空间离散化 (Q-Learning的关键步骤)
# CartPole有4个连续状态:[小车位置, 小车速度, 杆子角度, 杆子角速度]
# 我们为每个维度定义一个桶(bin)的数量,将其变为一个离散状态的元组。
DISCRETE_OS_SIZE = [20, 20, 20, 20]
# 状态空间的观察界限(根据CartPole环境特性定义)
obs_min = env.observation_space.low
obs_max = env.observation_space.high
# Q-Table 的形状:(20, 20, 20, 20, 2)
# 4个状态维度各20个桶,动作维度有2个动作
q_table = np.random.uniform(low=-2, high=0, size=(DISCRETE_OS_SIZE + [env.action_space.n]))
# 定义状态离散化函数
def get_discrete_state(state):
"""将连续状态映射到 Q-Table 中的离散索引"""
# 调整观测值范围,避免超过极限
state_adj = (state - obs_min) / (obs_max - obs_min)
# 将调整后的值映射到离散的桶索引
discrete_state = np.floor(state_adj * DISCRETE_OS_SIZE).astype(int)
# 确保索引在有效范围内 [0, DISCRETE_OS_SIZE - 1]
for i in range(len(discrete_state)):
discrete_state[i] = max(0, min(DISCRETE_OS_SIZE[i] - 1, discrete_state[i]))
return tuple(discrete_state)
# 3. 训练过程
for episode in range(EPISODES):
# 重置环境,获取初始状态
current_state, _ = env.reset()
discrete_state = get_discrete_state(current_state)
# 是否渲染画面 (可以每隔一段时间渲染一次,观察学习过程)
if episode % 2000 == 0:
print(f"Episode: {episode}")
render = True
env_render = gym.make("CartPole-v1", render_mode='human')
# 必须对新的环境实例调用 reset()
current_state, _ = env_render.reset()
discrete_state = get_discrete_state(current_state) # 重新获取离散状态
else:
render = False
env_render = env
done = False
truncated = False
while not done and not truncated:
# 探索与利用:根据 epsilon 决定是探索(随机)还是利用(Q值最大)
if np.random.random() > epsilon:
# 利用:选择当前状态下 Q 值最大的动作
action = np.argmax(q_table[discrete_state])
else:
# 探索:随机选择一个动作
action = env.action_space.sample()
# 智能体执行动作,环境返回新的状态、奖励、是否结束
new_state, reward, done, truncated, _ = env_render.step(action)
new_discrete_state = get_discrete_state(new_state)
# 4. Q-Table 更新 (核心学习公式)
if not done and not truncated:
# Q-Learning 更新公式:
# 新 Q 值 = 旧 Q 值 + 学习率 * ( 奖励 + 折扣因子 * max(下一状态的Q值) - 旧 Q 值 )
max_future_q = np.max(q_table[new_discrete_state])
current_q = q_table[discrete_state + (action,)]
new_q = (1 - LEARNING_RATE) * current_q + LEARNING_RATE * (reward + DISCOUNT * max_future_q)
q_table[discrete_state + (action,)] = new_q
# 如果回合结束,则更新终止状态的 Q 值
elif done or truncated:
q_table[discrete_state + (action,)] = reward # 终止状态 Q 值直接设置为奖励
discrete_state = new_discrete_state
# 5. 探索率衰减
if START_EPSILON_DECAY <= episode <= END_EPSILON_DECAY:
epsilon -= epsilon_decay_value
# 6. 训练结束,关闭环境
env.close()
print("Training finished.")
# 7. 评估并展示训练成果 (使用学到的策略进行一次模拟)
input("\n训练完成!按任意键观看最终成果:")
env_test = gym.make("CartPole-v1", render_mode='human')
# 运行 5 个回合进行观察
NUM_TEST_EPISODES = 5
total_score = 0
for test_episode in range(NUM_TEST_EPISODES):
state, _ = env_test.reset()
done = False
truncated = False
score = 0
# 打印提示信息,方便观察
print(f"\n--- 正在运行第 {test_episode + 1} 个测试回合 ---")
while not done and not truncated:
discrete_state = get_discrete_state(state)
# 此时不再探索,直接选择 Q 值最大的动作(利用)
action = np.argmax(q_table[discrete_state])
# 执行动作
state, reward, done, truncated, _ = env_test.step(action)
score += reward
# **【关键修改】添加延迟,减慢播放速度**
time.sleep(0.05)
total_score += score
print(f"回合 {test_episode + 1} 得分: {score}")
env_test.close()
print("\n所有测试回合完成。")
print(f"平均表现得分 (Average Score): {total_score / NUM_TEST_EPISODES}")
-
初始状态(探索为主): 在训练开始时,epsilon 接近 1,智能体几乎是随机选择动作(探索)。因此,杆子很快就会倒下,得分很低。
-
Q-Table 更新(学习): 每走一步,代码中的核心公式都会执行:
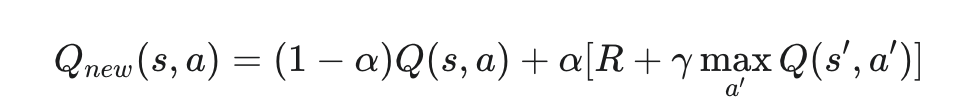
- 如果这次随机动作(a)导致了好的结果(杆子没倒,获得了 +1 奖励 R),并且下一状态 s′ 估计也很好(maxQ(s′,a′) 很高),那么当前状态动作对 Q(s,a) 的值就会被调高。
-
探索率衰减(从探索到利用): 随着训练回合的增加,epsilon 会逐渐减小。这意味着智能体越来越少地随机选择,而是更多地依赖 Q-Table 中记录的值来选择预期回报最高的动作(利用)。
-
最终成果: 经过数千回合的试错和 Q-Table 的不断调整,Q-Table 中存储的数值变得越来越准确,指导智能体能够在大多数状态下选择最优的动作来保持杆子直立更长时间。当您运行最后的评估代码时,就会看到小车能够相对稳定地平衡杆子。
运行可以看到渲染出来的game
训练结果,注意他的随机性,每次的表现效果都是不同的,action的随机性,环境的随机性
Episode: 0
Episode: 2000
Episode: 4000
Episode: 6000
Episode: 8000
Episode: 10000
Episode: 12000
Episode: 14000
Episode: 16000
Episode: 18000
Training finished.
训练完成!按任意键观看最终成果:1
--- 正在运行第 1 个测试回合 ---
回合 1 得分: 42.0
--- 正在运行第 2 个测试回合 ---
回合 2 得分: 26.0
--- 正在运行第 3 个测试回合 ---
回合 3 得分: 24.0
--- 正在运行第 4 个测试回合 ---
回合 4 得分: 25.0
--- 正在运行第 5 个测试回合 ---
回合 5 得分: 45.0
所有测试回合完成。
平均表现得分 (Average Score): 32.4
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)