生成式人工智能综述2——图像生成
Denoising Diffusion Probabilistic Models 的工作原理就像是观看一部冰雕融化的录像,然后学习如何倒着播放这部录像来魔法般地重建冰雕。正向过程 (融化):这很简单,就是一部正常的录像。你从一座精美绝伦的冰雕开始,随着时间流逝,它会逐渐融化,失去细节、棱角变得圆润,最后完全化成一滩水。这个过程遵循物理规律,是固定的、不可逆的。反向过程 (重建):这是魔法发生的地方
0.序言
这篇综述主要介绍图像生成部分,类似于文本生成,我们从图像生成的过去讲起,也就是VAE和GAN模型,然后介绍现在图像生成的几条技术路径,最后展望一下未来。
这里我们还是暂且不深入原理细节,专注于技术。至于扩散模型的公式推导以及control net等组件的具体原理将会另外补充一篇博客,和视频生成部分的细节一起。
1.图像生成的过去
1.1从AE到VAE
1.1.1Auto-encoder
自编码器(AE)是一种无监督学习模型,其主要目标是通过压缩和重建输入数据来学习数据的低维表示。其网络结构有两个重要的特征:
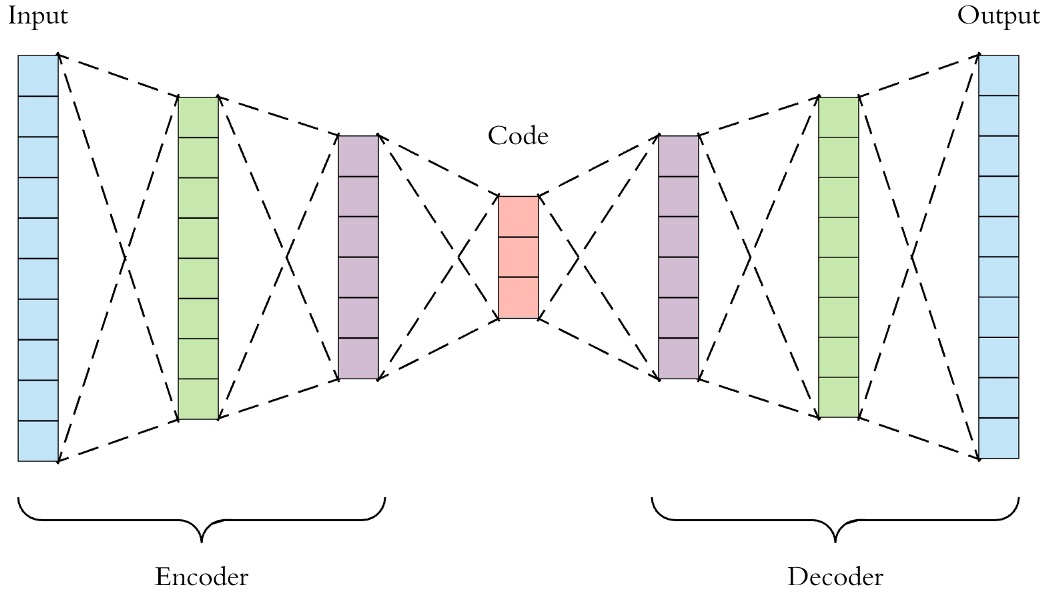
输出层神经元数量与输入层一致:
在传统的有监督学习中,输出层的神经元数量通常由任务的标签类别决定。然而,自动编码器作为无监督学习模型,其输出层的神经元数量往往与输入层一致。这保证了输出和输入的数据结构相同,便于比较输入与输出之间的差异,也便于直接检验输出数据是否携带了输入数据的关键信息。
例如,若输入是图像数据,输出层将输出与输入图像尺寸相同的图像,且输出图像应尽可能保留原图的结构和信息。通过视觉比对,便能判断输出图像是否成功保留了原始图像的关键特征。
网络结构呈现对称性:
与传统的深度神经网络不同,自动编码器的网络结构通常呈现出“大-小-大”的对称性。这意味着从输入到输出,数据首先经过编码器进行压缩(从高维到低维),然后经过解码器进行扩展(从低维到高维)。编码器和解码器的结构通常是对称的,其中中间层较为简单,而两端的结构较为复杂。这种对称性体现了数据压缩与重建的过程。
自动编码器的训练过程与传统的深度神经网络类似,它是一个有监督的过程,只不过没有标签数据。自动编码器的目标是最小化输入数据与重建数据之间的差异,通常使用反向传播算法,并且选用均方误差(MSE)作为损失函数。
我们假设编码过程是,解码过程是
。
这个自编码的意义在于
1.模型训练结束后,我们就可以认为编码z囊括了输入数据X的大部分信息,也因此我们可以直接利用表达原始数据,从而达到数据降维的目的。
2.解码器只需要输入某些低维向量,就能够输出高维的图片数据,那我们能否把解码器模型直接当做生成模型,在低维空间中随机生成某些向量,再由解码器来生成图片呢?
对于第二点,理论上可以这么做,但问题在于
1.绝大多数随机生成的z,f(z)只会生成一些没有意义的噪声,之所以如此,原因在于没有显性的对z的分布p(z)进行建模,我们并不知道哪些z能够生成有用的图片。
2.我们用来训练的数据是有限的,只会对极有限的z有响应。而整个低维空间又是一个比较大的空间,如果在这个空间上随机采样的话,我们自然不能指望总能恰好采样到能够生成有用的图片的
有问题自然便得探索对应的解决方案,而VAE(自变分编码器,Variational Auto-encoder)则是在AE的基础上,显性的对z的分布p(z)进行建模(比如符合某种常见的概率分布),使得自编码器成为一个合格的生成模型。
此外,如果没有对网络进行任何限制,自动编码器可能仅仅会学习到一种简单的映射,甚至直接“复制”输入数据。为了防止这种情况发生,通常会引入一些“干扰”或“正则化”技术,例如:
潜在空间的约束:在一些变种中,我们会对编码器输出的潜在表示施加一些约束,使得其不是一个简单的确定性输出,而是一个概率分布(如VAE)。
加入噪声:例如去噪自编码器(Denoising Auto-encoder,DAE)通过在输入数据中加入噪声来迫使模型学习更具泛化性的表示。
1.1.2Variational Auto-encoder
1.1.2.1变分推断Variational Inference
先来通俗的话(https://www.zhihu.com/question/41765860)——
首先,我们的原始目标是,需要根据已有数据推断需要的分布p;当p不容易表达,不能直接求解时,可以尝试用变分推断的方法, 即,寻找容易表达和求解的分布q,当q和p的差距很小的时候,q就可以作为p的近似分布,成为输出结果了。
在这个过程中,我们的关键点转变了,从“求分布”的推断问题,变成了“缩小距离”的优化问题。
再来公式推导——
我们经常利用贝叶斯公式求后验分布
但这样求解是比较困难的,因为我们需要去计算,这个积分计算起来非常困难(数据的联合分布往往是离散的)。在贝叶斯统计中,所有的对于未知量的推断(inference)问题可以看做是对后验概率的计算。因此提出了Variational Inference来计算后验分布。
那变分推断怎么做的呢?其核心思想主要包括两步:
1. 假设一个分布 (这个分布是容易计算的,不然就没意义了)
2. 通过改变分布的参数,使
靠近
。
总结称一句话就是,为真实的后验分布引入了一个参数化的模型。即:用一个简单的分布拟合复杂的分布
。
这种策略将计算p(z|x)的问题转化成优化问题了
收敛后,就可以用来代替
了。
1.1.2.2KL散度
而用一个分布去拟合另一个分布通常需要衡量这两个分布之间的相似性,通常采用 KL 散度。
相对熵(relative entropy)、KL 散度(Kullback–Leibler divergence)和信息散度(information divergence)都是同一个东西,是两个概率分布间差异的非对称性度量。在信息论中,相对熵等价于两个概率分布的信息熵的差值,若其中一个概率分布为真实分布,另一个为理论(拟合)分布,则此时相对熵等于交叉熵与真实分布的信息熵之差,表示使用理论分布拟合真实分布时产生的信息损耗。其公式如下:
合并之后表示为:
假设理论拟合出来的事件概率分布 q(x) 跟真实的分布 p(x)一模一样,即 p(x) = q(x),在理论拟合出来的事件概率分布跟真实的一模一样的时候,相对熵等于 0。而拟合出来不太一样的时候,相对熵大于 0。其证明如下:
其中第一个不等式是由推导出来的,只在
时取到等号。
这个性质很关键,因为它正是深度学习模型下降法需要的特性。假设神经网络拟合完美了,那么它就不再梯度下降,而拟合若不完美,则会因为它大于 0 而继续下降。
但它有不好的地方,就是它是不对称的。也就是用 P来拟合Q和用Q来拟合P的相对熵是不一样的,而距离是一样的。这也就是说,相对熵的大小并不与距离有一一对应的关系(非对称性)。
1.1.2.3变分推断求解
等式两边同时对Q(z)求期望,得:
我们的目标是使靠近
,就是求解:
而由于中包含 p(z|x),这项非常难求。借助上述公式的推导变形得到的结论:
将看做变量时,
为常量,所以,
等价于:
现在,变分推断的目标变成:
称为Evidence Lower Bound(ELBO)。p(x)一般被称之为 evidence,又因为
,所以
,这就是为什么被称为 ELBO。
1.1.2.4ELBO与VAE
然后我们将ELBO展开。
其中项为重建项,衡量VAE数据重建能力;项
为正则项,衡量参数化模型近似的分布与先验分布的差异。
通过上述推导,得到整体优化目标为:
即最大化ELBO,落实到VAE上写成损失函数即可。
其中为Decoder(生成网络)的参数,
表示Encoder的参数。上面期望的代与Auto-encoder的损失函数一模一样。所以就不讨论了,再稍微展开看一下KL散度部分。
下面是一个KL散度的结论,这里不做推导。
在VAE中的损失函数中先验分布为标准正态分布,所以
,q也为正态分布,
,代入散度计算公式中,则:
而为什么要进行正态分布的假设请看下一小节。
1.1.2.5另一个角度再看VAE
与普通自动编码器一样,变分自动编码器有编码器Encoder与解码器Decoder两大部分组成,原始图像从编码器输入,经编码器后形成隐式表示(Latent Representation),之后隐式表示被输入到解码器、再复原回原始输入的结构。然而,与普通Autoencoders不同的是,变分自用编码器的Encoder与Decoder在数据流上并不是相连的,我们不会直接将Encoder编码后的结果传递给Decoder,而是要使得隐式表示满足既定分布。
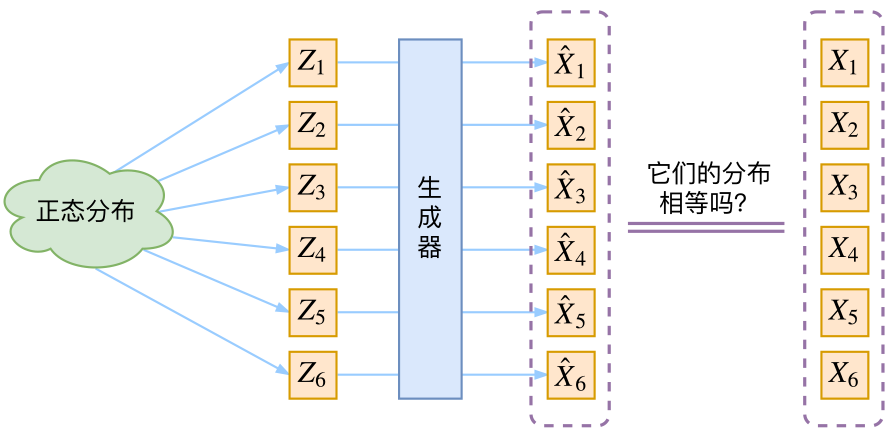
我们先假定从正态分布随机生成一组隐变量Z,然后经过生成器得到。因为这里没法保证
和
的对应关系,之前的均方误差就没法用了。那么VAE是怎么解决这个问题的呢?
其中一个模型用于原始输入数据的变分推断,生成隐变量概率分布
,而这一过程就要用到我们现在已经熟知的变分推断,称为推断网络。
而VAE的核心就是,我们不仅假设p(Z)是正态分布,而且假设每个也是正态分布。即针对每个采样点
获得一个专属于它和Z的一个正态分布
。
换言之,有k个X,就有k个正态分布,毕竟没有任何两个采样点是完全一致的,而后面要训练一个生成器,希望能够把从分布
采样出来的一个
还原为
。
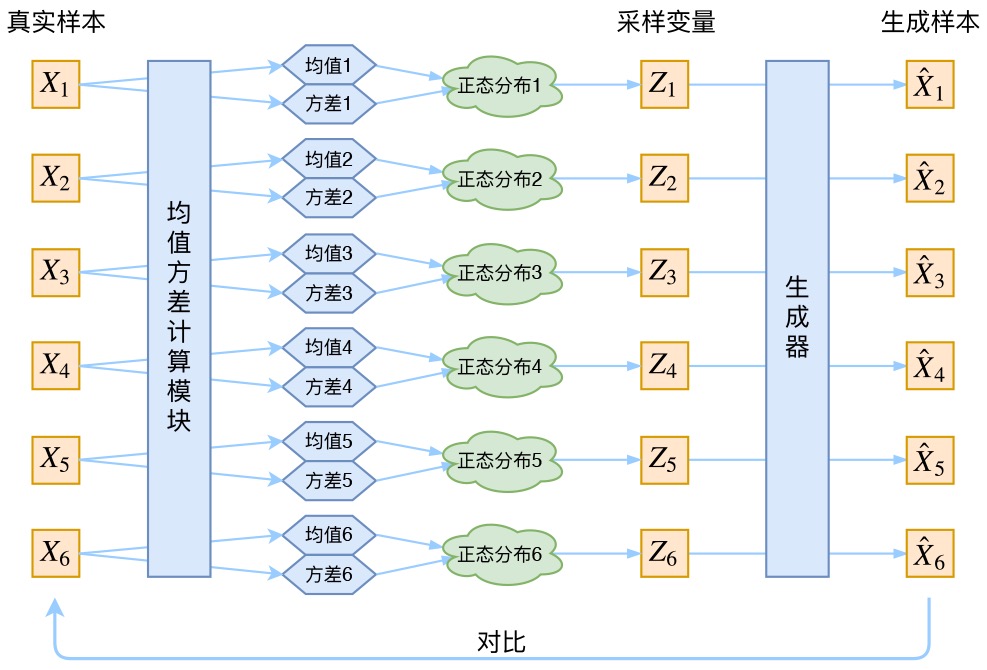
而如何确定这k个正态分布呢,众所周知,确定一个正态分布只需确定其均值和方差即可,故可通过已知的和 假设的Z去确定均值和方差,具体可以构建两个神经网络
,
(加log的话可正可负,不用加激活函数)去计算。
另一个模型,则根据生成的隐变量Z的变分概率分布p(Z),还原生成原始数据的近似概率分布称为生成网络
因为已经学到了这k个正态分布,那可以直接从分布中采样一个
出来,然后经过一个生成器得到
,那接下来只需要最小化方差
就行。
由于我们通过最小化来训练右边的生成器,最终模型会逐渐使得
和
趋于一致。但是注意,因为
是重新随机采样过的,而不是直接通过均值和方差encoder学出来的,这个生成器的输入Z是有噪声的。
1. 仔细思考一下,这个噪声的大小其实就用方差来度量。为了使得分布的学习尽量接近,我们希望噪声越小越好,所以我们会尽量使得方差趋于 0。
2. 但是方差不能为 0,因为我们还想要给模型一些训练难度。如果方差为 0,模型永远只需要学习高斯分布的均值,这样就丢失了随机性,VAE就变成AE了。
3. 那如何解决这个问题呢?其实保证有方差就行,但是VAE给出了一个优雅的答案:不仅需要保证有方差,还要让所有 p(Z|X)趋于标准正态分布,根据定义可知
这个式子的关键意义在于告诉我们:如果所有 p(Z|X)都趋于标准正态分布,那么我们可以保证 p(Z)也趋于标准正态分布,从而实现先验的假设,这样就形成了一个闭环!
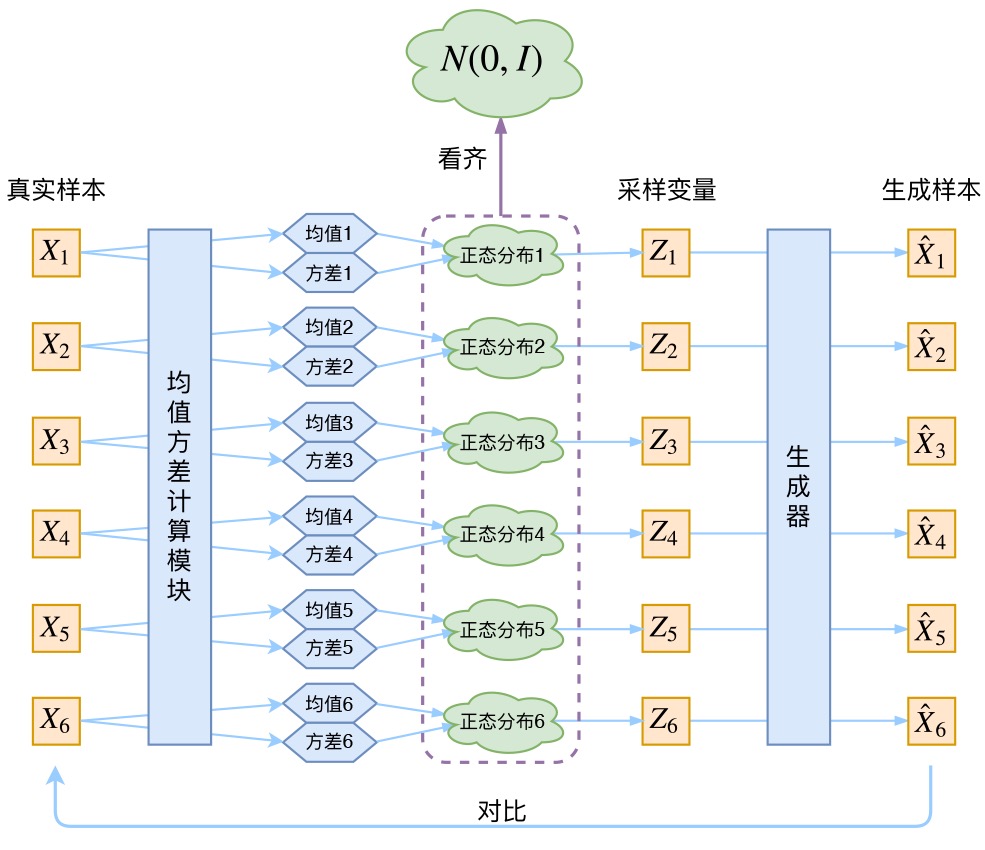
对均值的encoder添加高斯噪声(正态分布的随机采样),使得decoder(即生成器)有噪声鲁棒性
将所有趋近于标准正态分布,将encoder的均值尽量降为 0,而将方差尽量保持在1(矩阵层面上的单位矩阵),从损失函数里看其实可以说是KL正则项的作用。
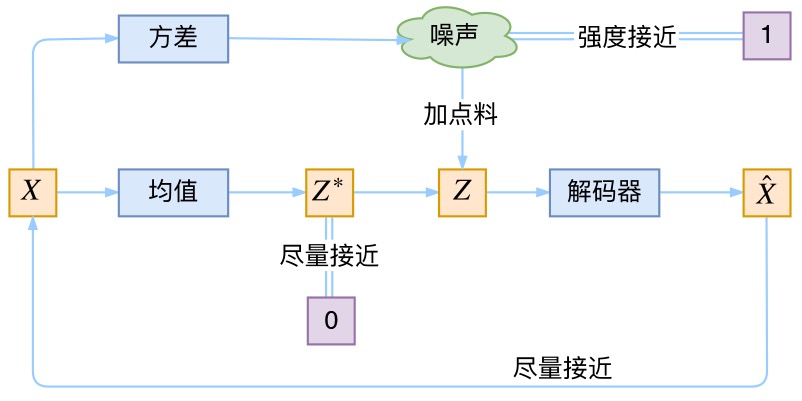
推荐阅读变分自编码器(一):原来是这么一回事 - 科学空间|Scientific Spaces
相信能让你对VAE的理解更上一层。
整体流程如下:
1.变分自动编码器中的编码器会尽量将样本X所携带的所有特征信息的分布转码成类正态分布。
2.编码器需要输出该类高斯分布的均值 与标准差作为编码器的输出。
3.以编码器生成的均值与标准差为基础构建正态分布。
4.从构建的正态分布中随机采样出一个数值Z,将该数值输入解码器。
5.解码器基于Z进行解码,并最终输出与样本的原始特征结构一致的数据,作为VAE的输出。
下面以单一样本和最简单的情况为例,简述一下VAE的正向传播过程。
首先,假设存在m个样本,5个特征,数据结构为(m,5)。同时,假设Encoder与Decoder中都只有2层带3个神经元的线性层,每个样本只生成一个均值与一个标准差,则转化流程如下所示:
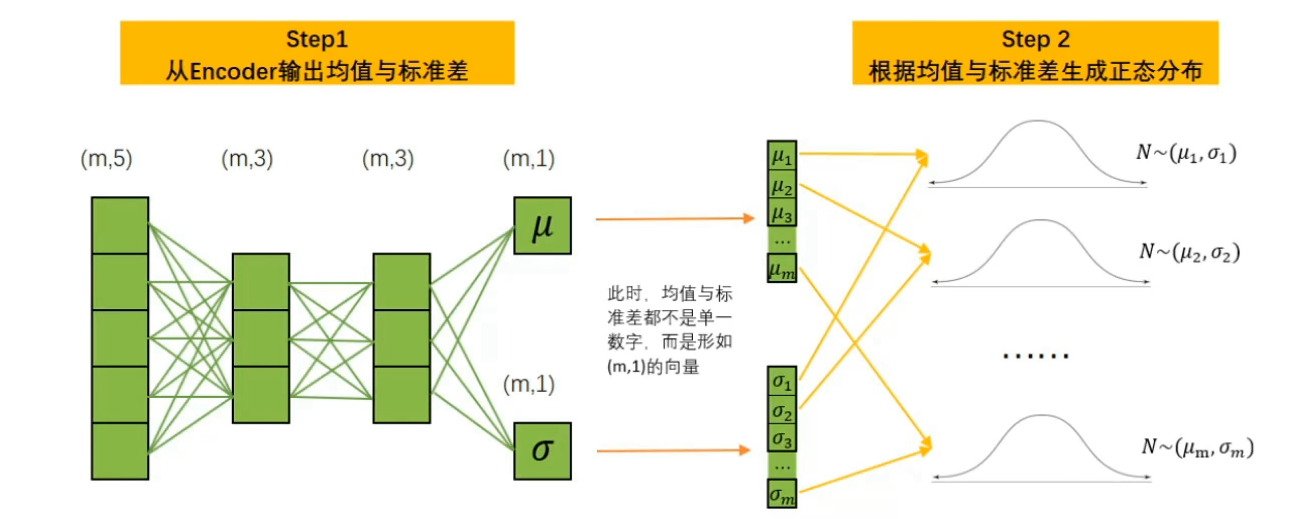
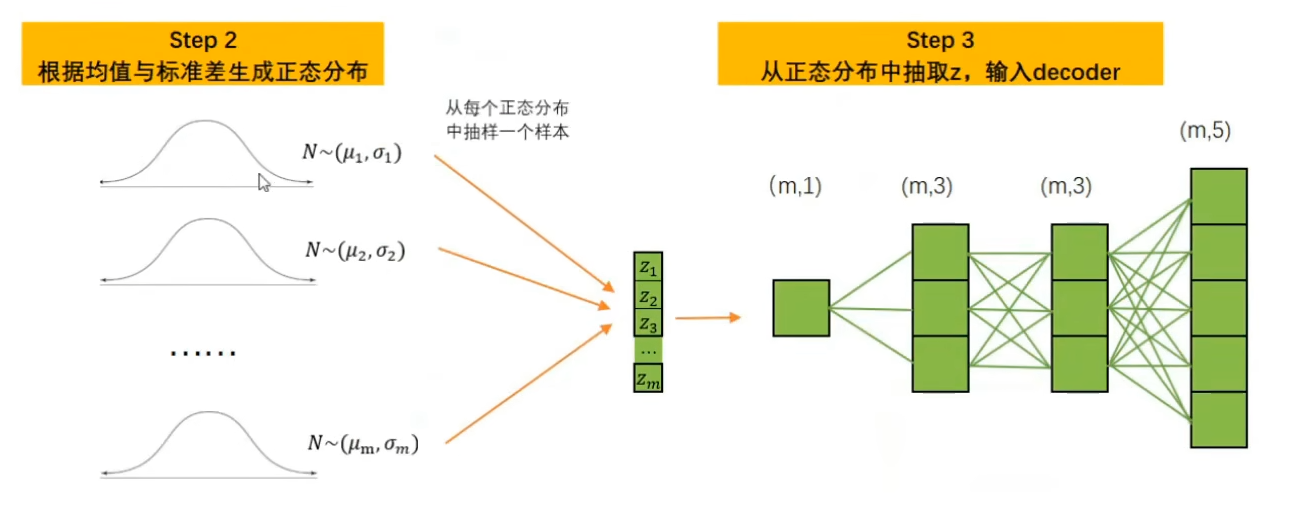
1.1.2.6重参数/再参数化(Reparameterization)
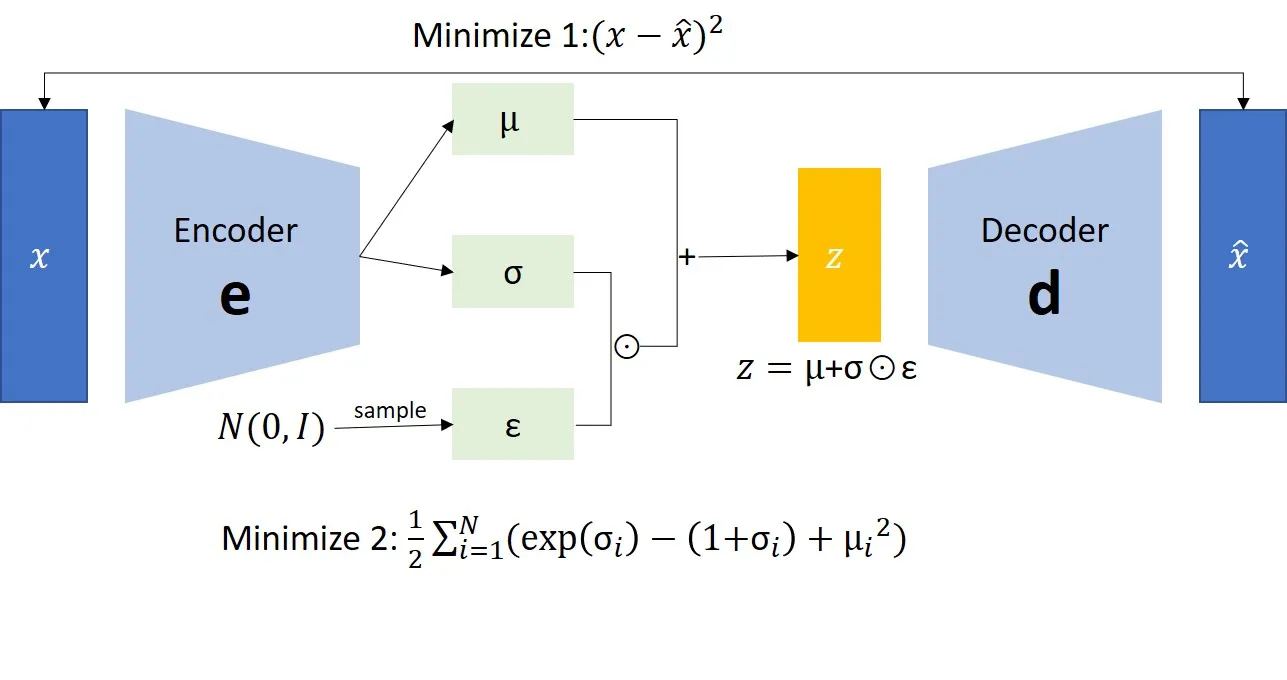
熟悉反向传播的朋友应该已经发现,编码器的输出和z之间是采样关系,并没有函数关系,因此实际上无法进行反向传播。而解决的方法很简单,名字叫重采样,如上图所示,采样的实际目标是一个正态分布的函数。这样就可以求z关于(
)的导数了。
将一个函数f(a)的参数a用另外一组参数表示b=g(b)。这样f(a)就换成参数为b的函数f(b)=f(g(b))。
想了解更多可以看这里。
https://zhuanlan.zhihu.com/p/628311865
1.2GAN
显示地构建出样本的密度函数,并通过最大似然估计来求解参数,称为显式密度模型(Explicit Density Model)。比如VAE的密度函数为
。虽然使用了神经网络来估计
,但是我们依然假设
为一个参数分布族,而神经网络只是用来预测这个参数分布族的参数。这在某种程度上限制了神经网络的能力。
如果只是希望有一个模型能生成符合数据分布的样本,那么可以不显示地估计出数据分布的密度函数。假设在低维空间Z中有一个简单容易采样的分布p(z),通常为标准多元正态分布。我们用神经网络构建一个映射函数
,称为生成网络。利用神经网络强大的拟合能力,使得
服从数据分布
。这种模型就称为隐式密度模型(Implicit Density Model)。所谓隐式模型是指并不对显示地建模
,而是直接建模生成过程。
隐式密度模型的一个关键是如何确保生成网络产生的样本一定是服从真实的数据分布。既然我们不构建显式密度函数,就无法通过最大似然估计等方法来训练。
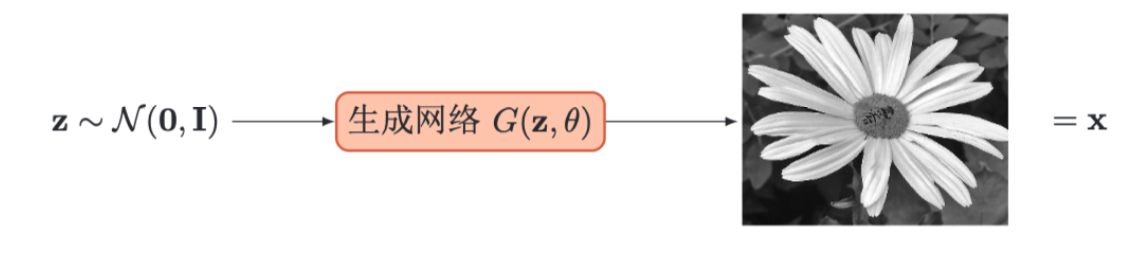
生成对抗网络(Generative Adversarial Networks, GANs)是通过对抗训练的方式来使得生成网络产生的样本服从真实数据分布。在生成对抗网络中,有两个网络进行对抗训练。一个是判别网络,目标是尽量准确地判断一个样本是来自于真实数据还是生成网络产生的;另一个是生成网络,目标是尽量生成判别网络无法区分来源的样本。这两个目标相反的网络不断地进行交替训练。当最后收敛时,如果判别网络再也无法判断出一个样本的来源,那么也就等价于生成网络可以生成符合真实数据分布的样本。
1.2.1判别网络
判别网络(Discriminator Network)的目标是区分出一个样本x时来自于真实分布
还是来自于生成模型
,因此判别网络实际上是一个两类分类器。用标签y = 1来表示样本来自真实分布,y = 0表示样本来自模型,判别网络
的输出为x属于真实数据分布的概率,即
则样本来自模型生成的概率为。
给定一个样本,
表示其来自于
还是
,判别网络的目标函数为最小化交叉熵,即最大化对数似然。
其中和
分别为生成网络和判别网络的参数。
1.2.2生成网络
生成网络(Generator Network)的目标刚好和判别网络相反,即让判别网络将自己生成的样本判别为真实样本。
上面的这两个目标函数是等价的。但是在实际训练时,一般使用前者,因为其梯度性质更好。我们知道,函数在x接近 1 时的梯度要比接近 0 时的梯度小很多,接近“饱和”区间。这样,当判别网络D以很高的概率认为生成网络G产生的样本是“假”样本,即
。这时目标函数关于
的梯度反而很小,从而不利于优化。
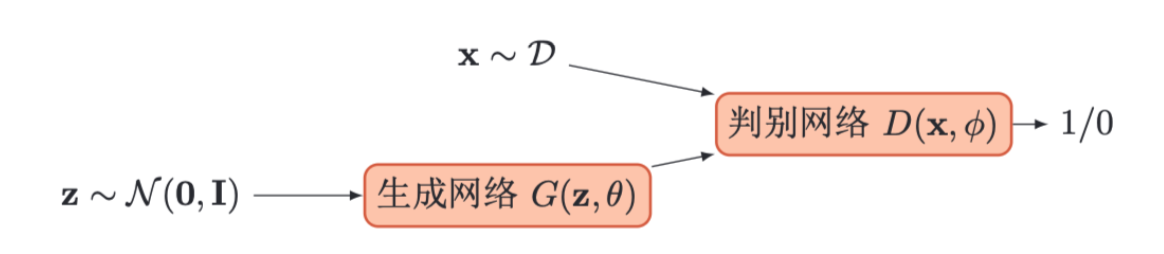
1.2.3训练
和单目标的优化任务相比,生成对抗网络的两个网络的优化目标刚好相反。因此生成对抗网络的训练比较难,往往不太稳定。一般情况下,需要平衡两个网络的能力。对于判别网络来说,一开始的判别能力不能太强,否则难以提升生成网络的能力。然后也不能太弱,否则针对它训练的生成网络也不会太好。在训练时需要使用一些技巧,使得在每次迭代中,判别网络比生成网络的能力强一些,但又不能强太多。
生成对抗网络的训练流程如算法13.1所示。每次迭代时,判别网络更新K次而生成网络更新一次,即首先要保证判别网络足够强才能开始训练生成网络。在实践中K是一个超参数,其取值一般取决于具体任务。
尽管GAN具有很大的潜力,但其训练过程面临一些挑战:
模式崩溃(Mode Collapse):生成器可能只生成少数几种样本,而不覆盖真实数据的全貌,导致生成的样本多样性较低。
训练不稳定:生成器和判别器的训练通常是非常不稳定的,可能出现梯度消失或梯度爆炸的问题。
收敛性问题:在某些情况下,GAN的训练过程可能无法收敛,导致模型无法生成高质量的样本。
1.2.4GAN的变种
为了克服原始GAN的一些问题,研究者提出了多个改进和变种,主要包括:
DCGAN(Deep Convolutional GAN):使用卷积神经网络(CNN)代替传统的全连接层来构建生成器和判别器,从而提高了生成图像的质量和稳定性。
WGAN(Wasserstein GAN):引入了Wasserstein距离(也称为地球移动距离,Wasserstein Distance)来改进GAN的训练稳定性和收敛性。
CGAN(Conditional GAN):通过引入条件变量(如标签信息)来生成特定类型的样本。CGAN可以控制生成内容的特定属性。
1.3连接文本和图像的视觉模型
在计算机视觉领域,随着深度学习的不断发展,研究者们不断探索更高效、更通用的视觉表示学习方法。这一部分将按顺序介绍三种具有代表性的模型:Vision Transformer(ViT)、Contrastive Language–Image Pretraining(CLIP)和Masked Autoencoders(MAE)。首先,ViT通过将图像切分为固定大小的“图像块”(patch),并借鉴Transformer在自然语言处理中的成功经验,实现了端到端的自注意力建模;随后,CLIP通过大规模的图像–文本对比学习,为视觉模型赋予了跨模态的理解与检索能力;最后,MAE以自监督的方式,通过随机掩码与重建策略,进一步提升了视觉特征的鲁棒性与泛化性能。三者各具特点,但均代表了视觉表示学习的重要方向,为下游任务提供了丰富而强大的基础。
1.3.1ViT
An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale
通过ViT的全称Vision Transformer我们就可以最直观的理解它的内容,就是将用于进行序列预测的transformer模型用在视觉任务上(这一直以来是CNN的主场)。
最简单能想到的做法就是直接把图像按像素块拆解,各个像素点之间两两做self-attention,但这样计算复杂度太过庞大,文本可以这样做是因为一句话的文本序列最多也就几百token,但一张224*224分辨率的图像就有50176个像素,再扩展到RGB三个维度的话更是没法计算。
之后自然就有人想到把网络中间的特征图(feature map)当做transformer的输入,但这样其实在逻辑上会产生矛盾。
我们知道卷积之后特征图的空间分辨率被逐渐降低,最终产生的特征图往往只保留了图像的高级语义信息,而缺乏足够的局部空间细节。但transformer依赖自注意力机制捕捉长程依赖,而如果输入的特征图已经缺乏充分的空间分辨率,transformer可能无法有效地恢复或捕捉图像的精细空间结构,从而导致性能下降。
那么ViT是怎么做的呢?同样直白,直接把图像切块(如论文题目),把图像块作为transformer的输入。
1.3.1.1ViT的架构
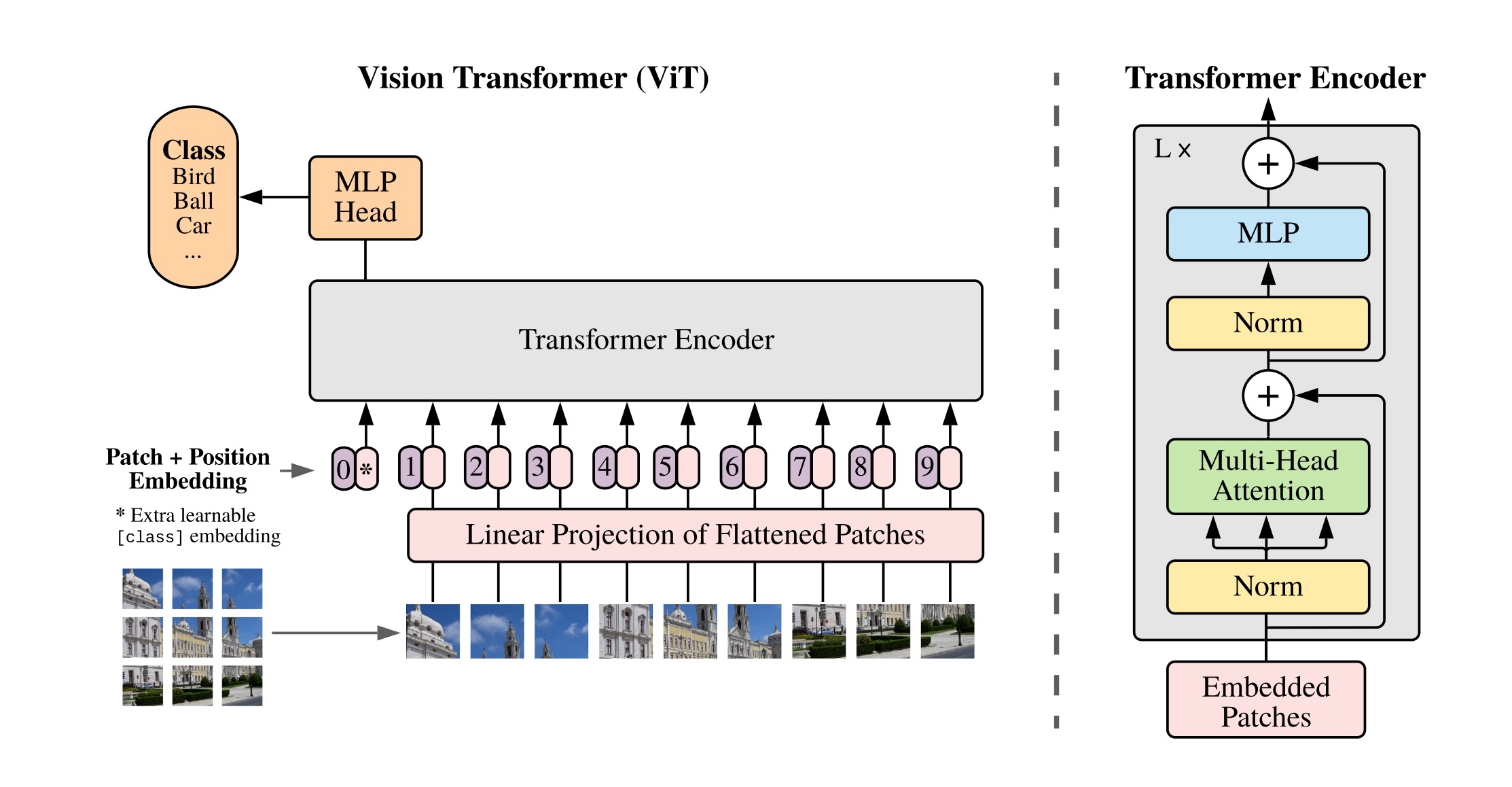
Embedding
以ViT_base_patch16为例,224*224的图片被分割成16*16的patch,总共产生196个patch。对于彩色图片的话需要考虑RGB通道,所以每个patch的维度是[16,16,3]。最后图片就从原来的[224,224,3]变成了[14,14,768]。然后经过flatten操作变成[196,768]。然后经过一个768*768的全连接层,所以处理之后还是[196,768]。
接下来,为了做最后的分类,在所有tokens的前面加一个可以通过学习得到的 [class] token作为这些patchs的全局输出,相当于BERT中的分类字符CLS,所有token两两之间都会做交互(self attention),故这个[class] token也会有与其他所有token交互的信息
且为了保持维度一致,[class] token的维度为 [1, 768] ,通过Concat操作,[196, 768] 与 [1, 768] 拼接得到 [197, 768]。
由于self-attention本身没有考虑输入的位置信息,无法对序列建模。而图像切成的patches也是有顺序的,打乱之后就不是原来的图像了,所以和transformer一样,就是对于这些 token 添加位置编码,在每个token前面加上位置向量(这里的加是直接向量相加即sum,不是concat),这里和 transformer 一致,都是可训练的参数,因为要加到所有 token 上,所以维度也是 [197, 768]。
Transformer Encoder
[197,768]的图像块编码就和通常的transformer一样,ViT_base_patch16的多头注意力设计的是12个头,每个头维度[197,64]。最后拼接起来回到[197,768]。最后经过一个4倍缩放的MLP层。
MLP Head
这里在原始论文是用tanh做非线性激活函数,根据[class]token做分类的预测。
更完整的流程图如下所示。
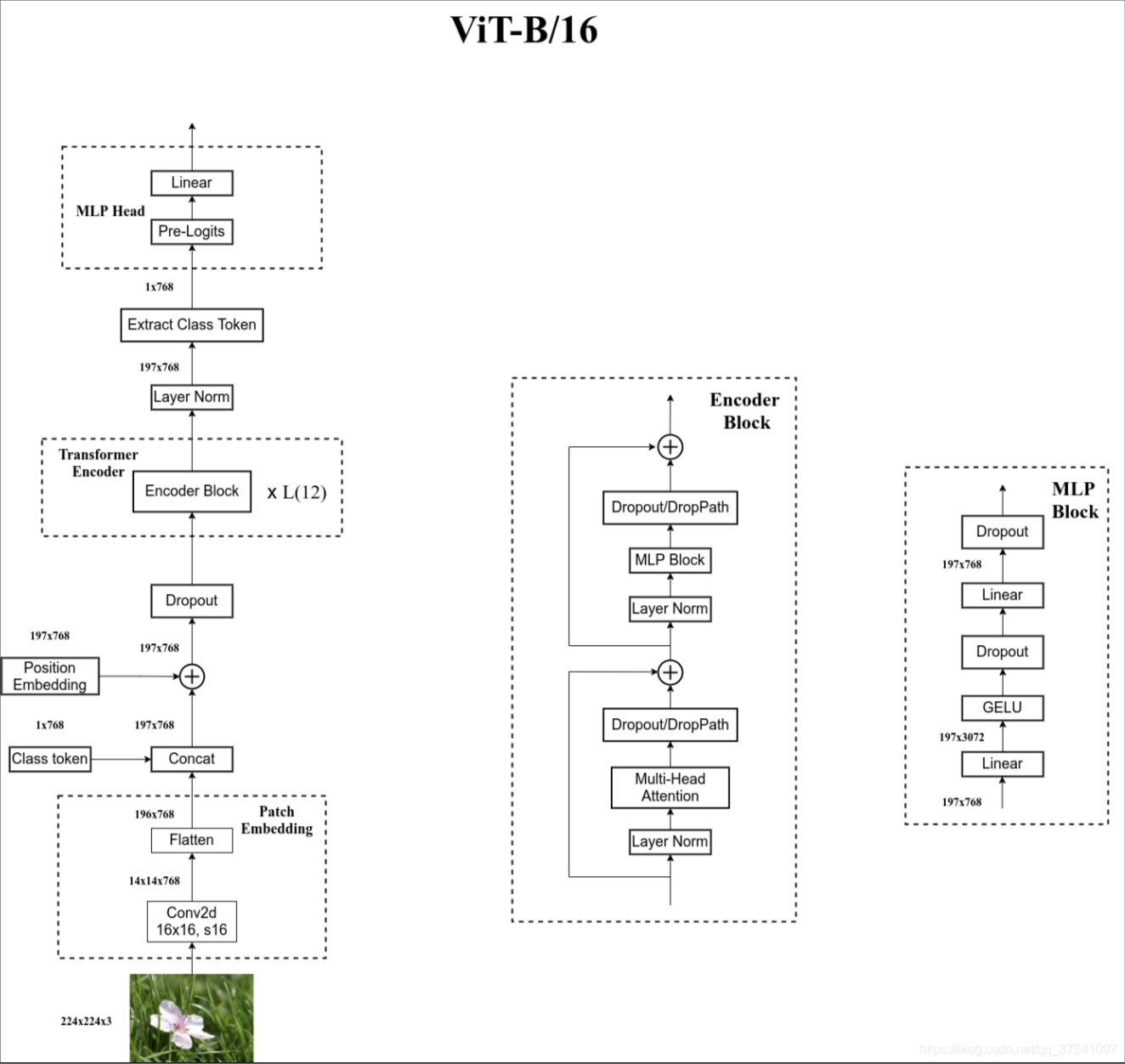
ViT原论文中最核心的结论是,当训练数据集规模不足时,ViT的表现通常略逊于同等大小的ResNet。这是因为相较于CNN,Transformer缺少一些归纳偏置。CNN具有两种归纳偏置,一是局部性:图片上相邻区域具有相似特征;二是平移不变性:卷积后平移和平移后卷积结果等效。这些归纳偏置为模型提供了更多先验信息,使得使用较少数据就能学习到良好模型。然而,当拥有足够大规模的数据集进行预训练时,ViT能够突破Transformer缺少归纳偏置的限制,并在下游任务中取得非常好的迁移效果。
1.3.1.2ViT与BERT对比
| 输入与处理步骤 | BERT | ViT |
|---|---|---|
| 输入 | 固定长度的一段文本序列 | 固定词向量大小的图像序列 |
| 向量嵌入 | 固定的词向量嵌入、可学习的位置嵌入、段嵌入 | 可学习的词向量嵌入、可学习的位置嵌入 |
| 特殊词元 | 最前端位置,固定嵌入向量 | 最前端位置,可学习嵌入向量 |
在ViT中,使用可学习的向量来表示词元而不是像BERT那样使用固定的向量:因为预训练是有监督的,使用可学习的向量来表示词元可以使模型更好地适应具体任务的特征。
1.3.2CLIP
Learning Transferable Visual Models From Natural Language Supervision
预训练的本质是学习一个压缩器,该压缩器通过挖掘不同数据之间的相似性并以高维结构表示这种相似性进行数据压缩。传统的有监督学习方法通过标签来定义这种相似性:使用压缩器将图像压缩到标签空间,并通过标签进行对齐。然而,这种经典做法存在一些问题:
1.在标签空间中,各个标签向量是正切的,这可能导致过度对齐图像。某些图片可能与多个类别非常相似,将其对齐到单一类别会导致大量语义信息的损失。
2.标签空间需要事先定义。传统的<图像,类别>样本形式要求在训练之前定义一个固定的标签空间,这使得预训练模型无法泛化到涉及其他视觉概念的图片上。
文本作为语义丰富的标签解决了上述两个问题。
因此,Contrastive Language-Image Pretraining(CLIP)模型采用文本作为监督信号,属于多模态学习的领域。该模型将文本和图像映射到一个共同的隐空间,以实现它们在语义上的对齐。与传统视觉概念相比,语义丰富的文本缺少了一些“归纳偏置”,例如文本标签不是独热向量,并且不同的文本标签之间也不是正交的。为了解决这个问题,像ViT一样,CLIP采用了海量的<图像,文本描述>样本进行训练。
CLIP由OpenAI在2021年1月发布。
通过超大规模模型预训练提取视觉特征,进行图片和文本之间的对比学习。预训练好之后不微调直接推理,在不使用ImageNet数据集的任何一张图片进行训练的的情况下,最终模型精度能跟一个有监督的训练好的ResNet-50打成平手 (在ImageNet上zero-shot精度为76.2%)。
1.3.2.1CLIP的训练(和GPT-3一样又是一个力大砖飞的奇迹)
为了训练CLIP,OpenAI从互联网收集了共4个亿的文本-图像对,论文称之为WIT(Web Image Text,WIT质量很高,而且清理的非常好,这也是CLIP如此强大的原因之一,后续在WIT上还孕育出了DALL-E模型)。
需要注意的是在这种多模态架构中,模型建模的不是p(y|x),而是p(d|x,y), 其中d表示他们是否属于同一个概念。
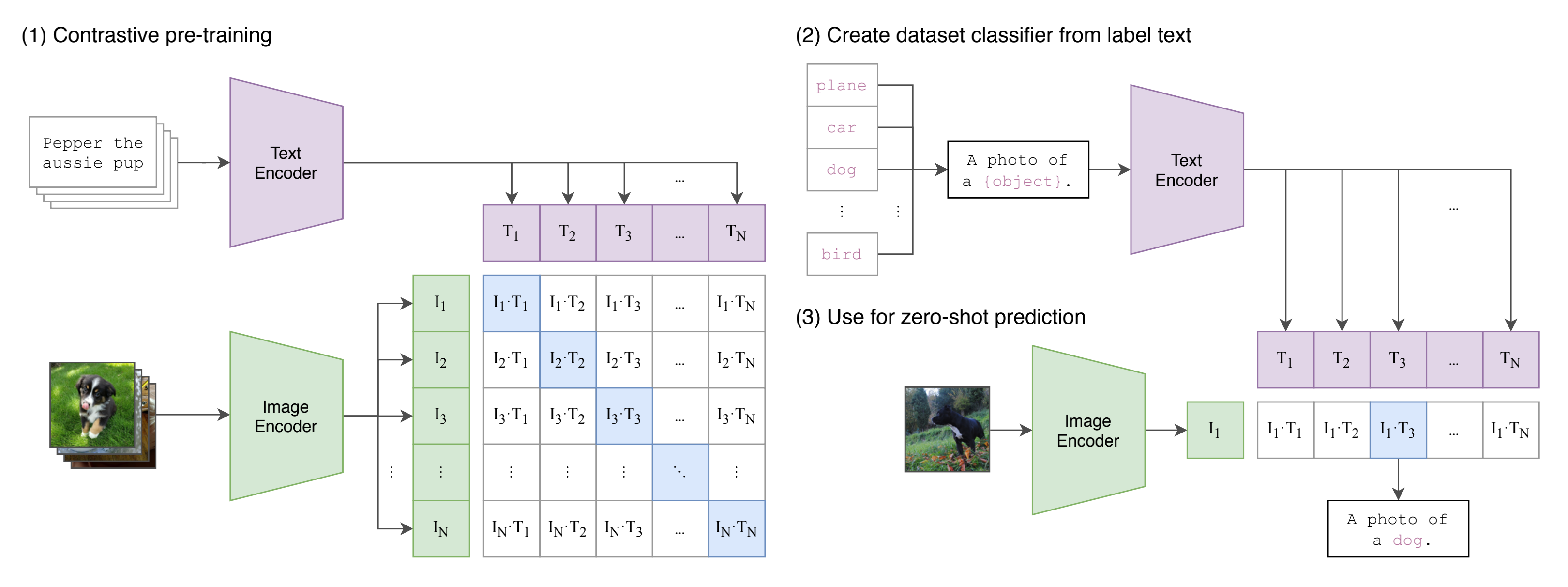
第一步的对比学习如图所示,CLIP的输入是一对对配对好的的图片-文本对(比如输入是一张狗的图片,对应文本也表示这是一只狗),这些文本和图片分别通过Text Encoder和Image Encoder输出对应的特征。然后在这些输出的文字特征和图片特征上进行对比学习。
互相配对的图像–文本对是正样本(上图输出特征矩阵对角线上标识蓝色的部位),其它对样本都是负样本,这样模型的训练过程就是最大化个正样本的相似度,同时最小化个负样本的相似度
Text Encoder可以采用NLP中常用的transformer模型
而Image Encoder可以采用常用CNN模型或者vision transformer等模型
相似度是计算文本特征和图像特征的余弦相似性
之后,CLIP可以直接实现zero-shot的图像分类,即不需要任何训练和微调,其实现zero-shot分类只需要简单的两步。
根据任务的分类标签构建每个类别的描述文本:A photo of {label},然后将这些文本送入Text Encoder得到对应的文本特征,如果类别数目为n,那么将得到n个文本特征。
将要预测的图像送入Image Encoder得到图像特征,然后与n个文本特征计算缩放的余弦相似度(和训练过程保持一致),然后选择相似度最大的文本对应的类别作为图像分类预测结果
进一步地,可以将这些相似度看成logits,加一步softmax后就可以到每个类别的预测概率。
是不是很直白...
1.3.2.2CLIP损失函数的伪代码
# image_encoder - ResNet or Vision Transformer
# text_encoder - CBOW or Text Transformer
# I[n, h, w, c] - 输入图片维度
# T[n, l] - 输入文本维度,l表示序列长度
# W_i[d_i, d_e] - learned proj of image to embed
# W_t[d_t, d_e] - learned proj of text to embed
# t - learned temperature parameter
# 分别提取图像特征和文本特征
I_f = image_encoder(I) #[n, d_i]
T_f = text_encoder(T) #[n, d_t]
# 对两个特征进行线性投射,得到相同维度的特征d_e,并进行l2归一化,保持数据尺度的一致性
# 多模态embedding [n, d_e]
I_e = l2_normalize(np.dot(I_f, W_i), axis=1)
T_e = l2_normalize(np.dot(T_f, W_t), axis=1)
# 计算缩放的余弦相似度:[n, n]
logits = np.dot(I_e, T_e.T) * np.exp(t)
# symmetric loss function
labels = np.arange(n) # 对角线元素的labels
loss_i = cross_entropy_loss(logits, labels, axis=0) # image loss
loss_t = cross_entropy_loss(logits, labels, axis=1) # text loss
loss = (loss_i + loss_t)/2 # 对称式的目标函数1.3.2.3CLIP的优势
跨模态检索:由于图像和文本共享相同的嵌入空间,CLIP可以进行跨模态检索。例如,你可以输入文本查询来找到相关的图像,反之亦然。
零样本学习(Zero-Shot Learning):CLIP能够在没有针对特定任务进行微调的情况下,直接对新任务进行预测。这意味着它能够处理新类别的任务,而无需为每个新任务重新训练。
强大的迁移能力:CLIP在多个下游任务中表现出色,如图像分类、目标检测、图像生成等。它可以通过与其它模型结合,提供出色的任务性能。
1.3.3MAE
Masked Autoencoders Are Scalable Vision Learners
因为文本之间的相关性,生成式自监督在LLM预训练中被广泛采用,这种自监督方式无需任何标签且效果显著。然而,LVM采用这种方法却面临重大困难,作者提出了以下原因:
与自然语言中经过人脑压缩的富语义单词相比,图像的信息密度较低且存在大量冗余信息。基于此结构,一个图像块的生成很可能完全依赖于其周围的图像块,而不是全局的语义信息。
基于这一假设,作者采用了极高的掩码率(75%)来减少图像中的信息冗余,使得一个图像块无法仅仅依赖于局部信息进行生成,而必须依赖于全局信息。此外,采用极高的掩码率还可以加快计算速度。

1.3.3.1MAE的结构
Masked Autoencoder(MAE)的encoder部分是一个标准的ViT(多层堆叠)。不同的是,这里的输入不是全部像素块而只包含未被遮蔽的25%的像素块,节省了计算开销。
由于解码器需要重构那些被遮蔽的像素,因此输入包含两部分的信息:未被遮蔽的像素块通过编码器生成的特征向量和被遮蔽的像素块信息。被遮蔽的像素块信息全部通过一个相同的可被学习的特征向量表示。 在这里,Decoder实质上还是一个包含Transformer block的架构(单层),因此输入向量包含了位置编码。该解码器只在预训练阶段使用,在迁移到下游任务时,解码器可以根据用户的实际需求替换成任意架构(也就是说我们真正需要的是编码器)。
解码器的最后一层是线性层。假设patch的大小是16×16,则线性层的输出维度就为256,然后再reshape为16×16,则得到了重构后的像素块。损失函数是MSE函数。只在被遮蔽的像素块上计算损失,因为未被遮蔽的像素块信息已经作为输入被编码器和解码器知晓。
上图简要展示了整个实现流程。将输入序列进行Linear Projection并加上位置编码形成一个个token后,进行shuffle操作,然后选取前25%的token作为Encoder的输入,便完成了随机采样过程。将Encoder的输出和表示被遮蔽的像素块的向量拼接,进行unshuffle操作,即还原原始像素块的排列顺序,然后再加入位置编码,送入Decoder中,完成像素重构。
1.3.3.2MAE的优势
(1)Scalable:encoder只操作可见patches,把mask tokens给本身参数就不多的decoder去运算,大大降低了计算量,尤其当mask的比例很高的时候,大大减少了预训练时间,让MAE可以很轻松的scale到更大的模型上(enabling us to easily scale MAE to large models),并且通过实验发现随着模型增大,效果越来越好
(2)高容量且泛华性能好(very high-capacity models that generalize well):使用MAE预训练方法,可以训练很大的model,比如ViT-Large/Huge,当把预训练好的ViT-Huge迁移到下游任务时,模型表现非常好,甚至超过了使用监督预训练的相同模型(achieves better results than its supervised pre-training counterparts),这说明MAE预训练学习到的表示可以很好的泛化到下游任务(these pre-trained representations generalize well to various downstream task)
2.图像生成的现在
虽然目前在图像生成方面基本上是扩散模型独领风骚,但是自回归路径依然有不少产出,尤其值得注意的是Visual AutoRegressive Modeling甚至获得了NeurIPS 2024 Best Paper Award。所以还不能称得上一家独大,类似于英伟达和AMD的关系。
自回归图像生成的开源模型,同时也是获奖的论文如下。
https://github.com/FoundationVision/Infinity
2.1自回归路径
完整了解的话有两篇比较近的综述值得推荐。
Autoregressive Models in Vision: A Survey
A Survey on Vision Autoregressive Model
虽然说了这么多,但这里就只介绍DALL-E最有代表性的早期研究,之后的方法大抵上也是在这个路线上继续的。
2.1.1DALL-E
熟悉的朋友应该发现我介绍东西喜欢根据名字去追根溯源,因为这样比较好记。不过到DALL-E这里就不太一样了...最贴切的来源是皮克斯动画电影《WALL·E》(《机器人总动员》)和西班牙超现实主义艺术家萨尔瓦多·达利(Salvador Dalí)的名字组合。
不过它还是多少有一个缩写的...DALL·E 的全称为 “Decoder-Only Autoregressive Language and Image Synthesis”,即“仅解码器自回归语言与图像合成”。嗯...我想你们能明白我想吐槽的点。
2.1.1.1dVAE
在DALL-E中,当用户输入一个提示,比如“一个牛油果形状的扶手椅”,这个文本首先被送入BPE编码器。该编码器使用一个预先定义好的词汇表(在DALL-E中包含16,384个标记)将文本分解成一个标准化的、最多包含256个数字标记的序列。这个过程确保了庞大而多变的语言世界能被表示为一种有限的、对模型来说易于管理的格式。而dVAE与此相同。
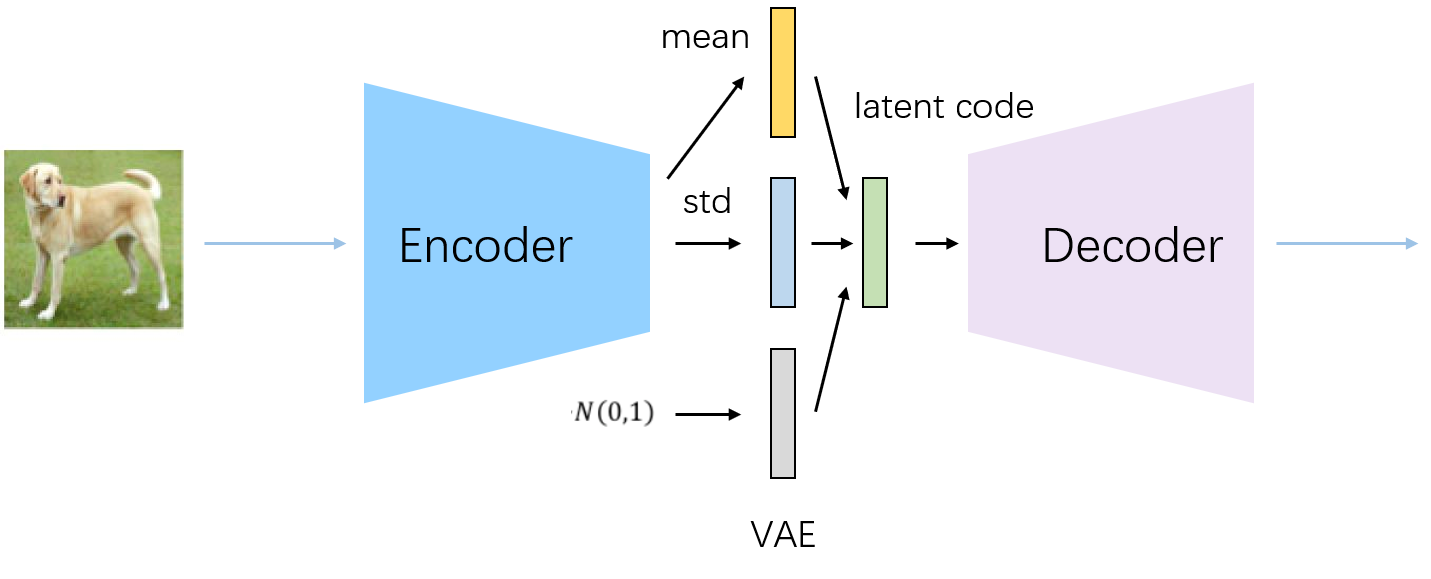
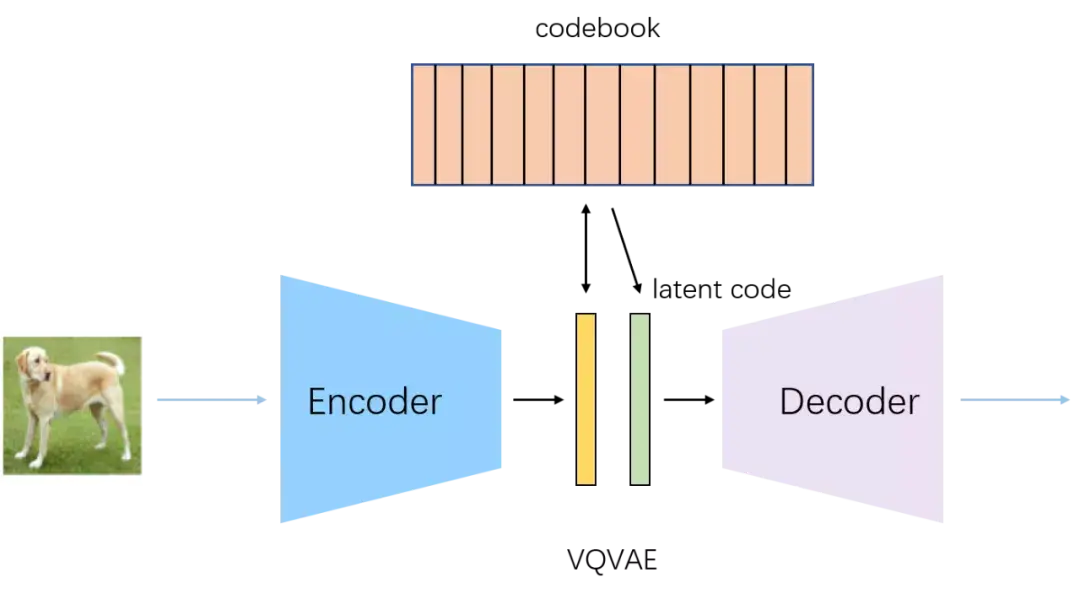
图像压缩: dVAE被训练用于将一张256x256像素的图像压缩成一个更小的32x32网格的“视觉标记”(visual tokens)。
创建视觉词汇表: dVAE有一个“码本”(codebook)或称“视觉词典”(在DALL-E中包含8,192个可能的标记)。对于32x32网格中的1,024个位置,每个位置都会被赋予词典中最能代表原始图像对应区域块的那个标记。这有效地将连续的、高维度的像素数据转换为了一个由1,024个离散视觉标记组成的序列。
2.1.1.2DALL-E的整体流程
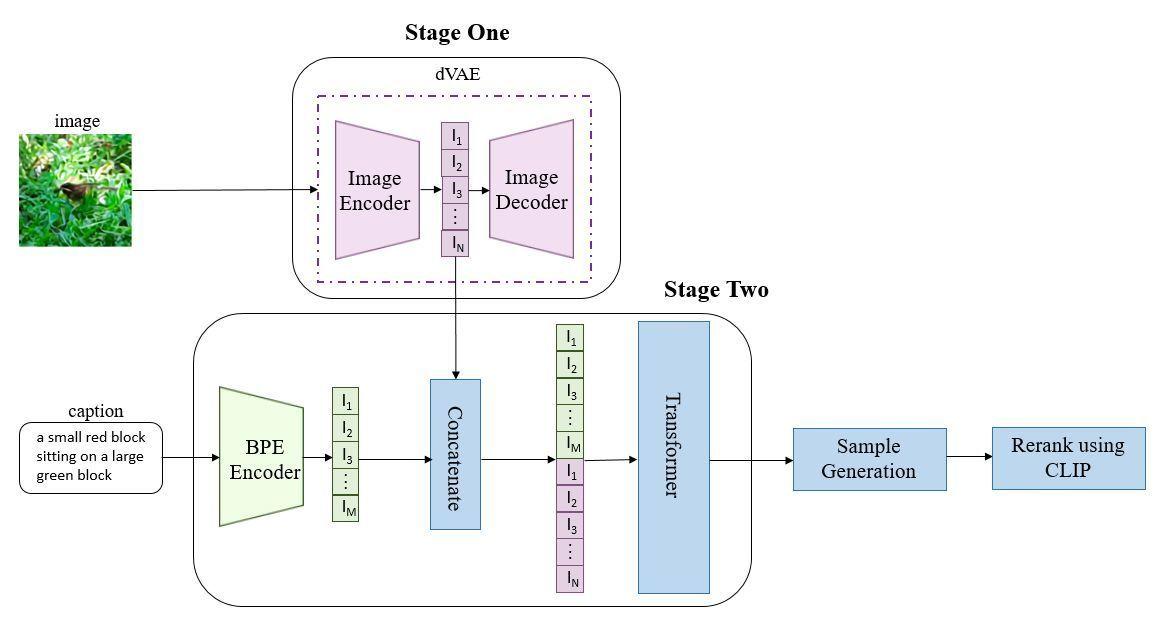
1.DALL-E 首先使用一个离散变分自编码器 (dVAE) 来将 256x256 像素的图像压缩成一个 32x32 的离散视觉标记 (visual tokens) 网格。dVAE 包含一个编码器,它将图像块映射到从一个包含 8192 个元素的“视觉词典”中选出的标记;以及一个解码器,它能将这些标记还原为图像。这一步至关重要,它将连续的、高维度的像素空间转化为了离散的、低维度的标记序列,使得强大的序列模型可以介入。
2.DALL-E 的核心是一个拥有 120 亿参数的 GPT-3 风格的 Transformer 模型。该模型接收一段经过处理的文本提示和部分已生成的视觉标记作为输入,然后以自回归的方式(即一个接一个地)预测下一个最有可能的视觉标记。整个生成过程就是将文本标记和视觉标记拼接成一个单一的序列,并由 Transformer 模型来完成这个序列。
3.推理阶段,给定一张候选图片和一条文本,通过transformer可以得到融合后的token,然后用dVAE的decoder生成图片,最后通过CLIP计算出文本和生成图片的匹配分数,采样越多数量的图片,就可以通过CLIP得到不同采样图片的分数排序,最后找到跟文本最匹配的图片。
2.1.2自回归图像生成模型的优势
虽然我个人觉得需要自己阐述优势的时候就是式微的时候...┓( ´∀` )┏
1.核心优势:闪电般的生成速度(虽然扩散模型最近速度也很惊人了)
自回归模型最显著的优势在于其快速的采样和生成能力。其工作原理类似于语言模型,通过顺序预测图像中的下一个像素或图像块(patch)来构建整个画面。这种一次性的、单向的生成过程,避免了扩散模型所需的大量迭代去噪步骤。
以当前主流的扩散模型为例,为了从纯噪声中还原出一张高清图像,往往需要执行数十甚至上百次的去噪迭代,这一过程是计算密集且耗时的。相比之下,自回归模型一旦训练完成,其生成图像的过程是一个直接的前向传播,能够很轻易迅速地完成。
2.明确的概率密度估计
自回归模型在理论层面也具备独特优势。它们能够对数据分布进行明确的(tractable)似然估计。这意味着模型可以直接计算出给定一张图像的概率,这对于需要精确概率评估的应用(如数据压缩和异常检测)至关重要。
当然任何事都是两面的,概率密度并不完备也同样导致其多样性相对较差。当然,自回归模型还可以借鉴之前transformer力大砖飞的效果。不过即使是openai也在DALL-E2转向了扩散模型。
2.2扩散路径
2.2.1DDPM简要介绍
Denoising Diffusion Probabilistic Models 的工作原理就像是观看一部冰雕融化的录像,然后学习如何倒着播放这部录像来魔法般地重建冰雕。
正向过程 (融化):这很简单,就是一部正常的录像。你从一座精美绝伦的冰雕开始,随着时间流逝,它会逐渐融化,失去细节、棱角变得圆润,最后完全化成一滩水。这个过程遵循物理规律,是固定的、不可逆的。
反向过程 (重建):这是魔法发生的地方。我们要训练一个AI模型,让它成为一位“时间魔术师”。这位魔术师只看着眼前这滩水,或者半融化的冰块,就能准确地推断出它上一秒钟的样子,并把它变回去。通过一步步地倒转时间,最终从一滩水中重建出完整的冰雕。
DDPM 就是通过学习这个“时间倒流”的魔法来实现图像生成的。
2.2.1.1正向过程
这个过程是固定不变的,不需要学习。它的目标是像冰雕融化一样,通过多步逐渐向一张真实的、清晰的图像中注入高斯噪声,直到它变成一幅完全看不出内容的“水”,也就是纯粹的噪声图。
输入:一张清晰的、真实的图像 $x_0$(一座完美的冰雕)。
过程:从第 t=1步到第 t=T步,每一步都在前一步图像的基础上,添加一点点符合高斯分布的噪声(让冰雕“融化”一点点)。
这里,是第t步时的图像(部分融化的冰雕),
是它前一步的样子。
是随机噪声(代表那一瞬间的融化方式),而
是一个预先设定的、非常小的常数,它控制着每一步“融化”的速度。定义
输出:经过 T步后,原始图像 就变成了一张纯粹的噪声图
(一滩水),其分布可以近似看作标准高斯分布。
这个“融化”过程有一个很棒的数学特性:我们可以通过一个公式,直接从最初的冰雕计算出任意中间时刻 t的“半融化”状态
,而不需要一步步模拟。
把上述公式迭代变换下,可以直接得出到
的公式,如下:
其中,
也是一个高斯噪声。
换言之,所以在
条件下的分布就是均值为
,方差为
的正态分布,这样只需要给出
,便可以计算出任意时刻t的
2.2.1.2反向过程
这是 DDPM 的精髓所在,整个学习和生成都在这个阶段。模型的目标是学习如何逆转上述的“融化”过程。
-
输入:一滩纯粹的随机噪声
(一滩水)。
-
目标:从
出发,一步步地逆转融化过程,经过T步,最终生成一张清晰、真实的图像
(重建冰雕)。
模型如何学习“重建”的魔法?
直接让神经网络预测出前一刻的清晰图像非常困难。DDPM 的天才之处在于它转换了任务:不预测上一刻的图像,而是预测在这一步融化时,具体是哪一阵“热风”(噪声)吹了过来。
这个任务就简单多了。模型(通常是一个 U-Net 架构的神经网络)的训练过程如下:
-
随机采样:从训练集中随机抽取一张真实图像
(一座真实的冰雕)。
-
随机“融化”:随机选择一个时间步t,然后通过正向过程的公式,直接计算出
在“融化”了 $t$ 步后的样子,得到带噪图像
和导致这次融化的具体“热风”模式
。
-
预测“热风”:将“半融化的冰雕”
和当前的时间步t一起输入到 U-Net 模型中。模型的任务就是预测出在第 2 步中导致融化的那股“热风”
。
-
计算损失:比较模型预测出的噪声和第 2 步中实际使用的噪声
之间的差距(通常用均方误差 MSE Loss)。这个差距就是魔术师的“失误”,模型会根据这个失误来调整自己的参数,提升“法力”(反向传播)。
通过在所有真实图像和所有时间步t上重复这个练习,U-Net 模型最终学会了:无论给它看任何时刻t的任何一座“半融化”的冰雕 ,它都能准确地推断出导致它变成这样的那股“热风”(噪声)是什么。
2.2.1.3Unet简介
U-Net 的名字来源于其独特的、对称的 U 形网络结构。这个结构是其高效工作的关键,主要由三个部分组成:
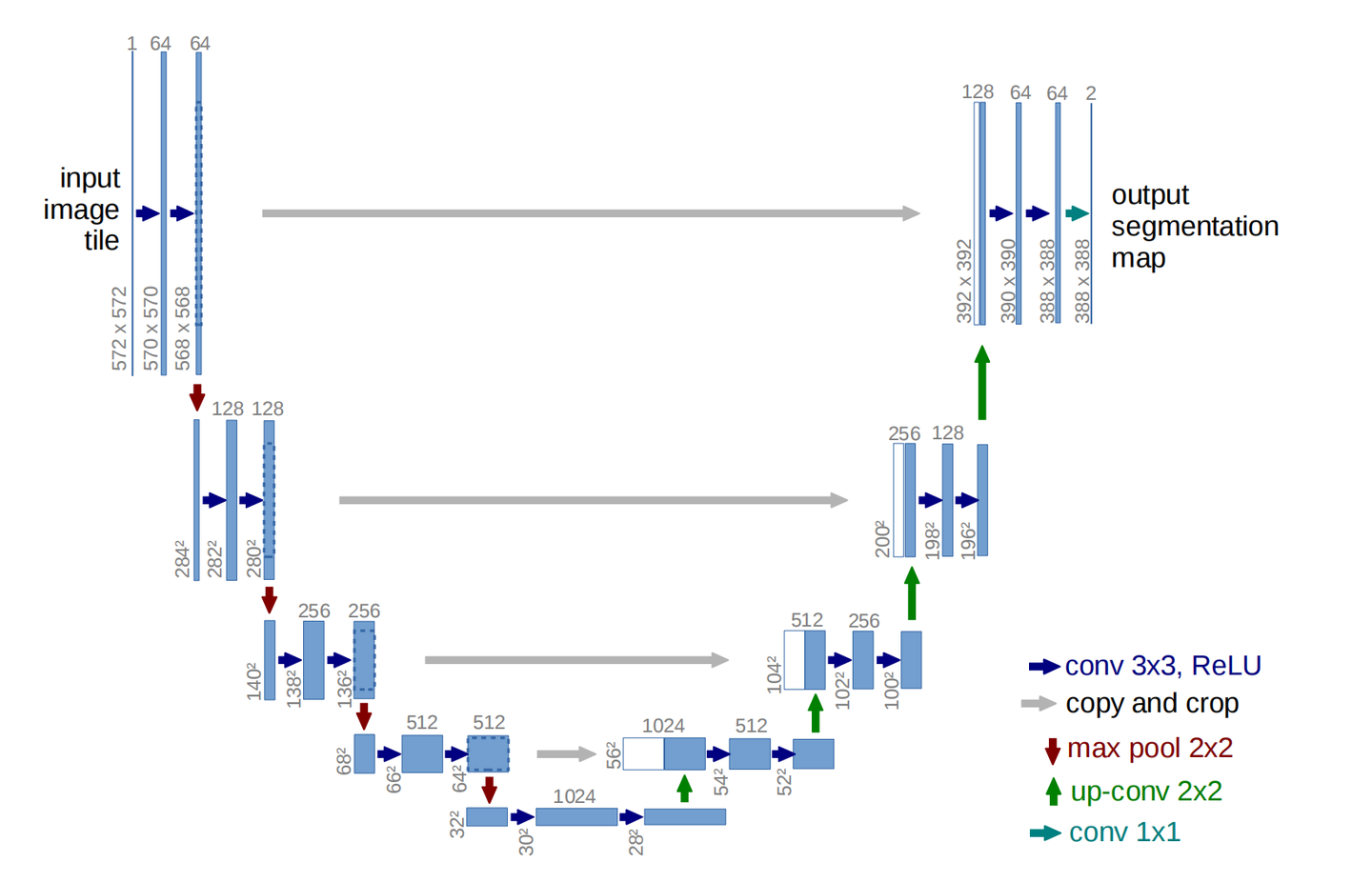
1. 收缩路径 (Contracting Path / Encoder) - 左侧的“U”
这部分的作用是理解图像的“内容”是什么。
-
工作方式:它就像一个标准的卷积神经网络(CNN)。通过一系列的卷积层和池化层(Pooling),它不断地对输入图像进行压缩和下采样。
-
目的:在这个过程中,图像的尺寸会变小,但特征图(Feature Map)的深度(通道数)会增加。这使得网络能够从图像中捕捉到从低级的纹理、边缘信息,到高级的、更抽象的语义信息(比如“这是一只猫的轮廓”)。这个“压缩”的过程帮助网络理解图像的全局上下文,但会丢失掉一些精确的位置信息。
你可以把它想象成**眯着眼睛看一眯着眼睛看一幅画:你可能看不清画的每一个细节,但你能快速把握画面的整体内容和布局。
2. 扩张路径 (Expansive Path / Decoder) - 右侧的“U”
这部分的作用是进行精细的“像素级修复”。
-
工作方式:它与收缩路径完全相反。通过一系列的上采样(Upsampling)或反卷积(Transposed Convolution),它逐步地将特征图放大,直到恢复到和原始输入图像完全相同的尺寸。
-
目的:这个“放大”的过程旨在将前面理解到的抽象内容,重新定位回像素空间,为每个像素做出分类或预测。例如,确定“这个像素点属于癌细胞”还是“这个像素点属于背景”。
这就像你凑近画布,拿着画笔开始精雕细琢,把之前眯眼看到的整体构思,一笔一笔地画出来。
3. 跳跃连接 (Skip Connections) - 连接左右的“横线”
这是 U-Net 的点睛之笔,也是其成功的核心。
-
工作方式:它将收缩路径中、在下采样之前生成的“高分辨率”特征图,直接复制并拼接到扩张路径中对应尺寸的特征图上。
-
目的:这个操作解决了深度学习中的一个关键问题。收缩路径虽然理解了“是什么”,但丢失了“在哪里”的精确位置信息。而这些被跳跃连接传递过来的早期特征图,正好包含了丰富的、未被压缩的细节和空间信息。通过将两者结合,扩张路径既能利用高层的语义信息(知道要画什么),又能利用底层的细节信息(知道该画在哪里),从而实现极其精准的分割和重建。
这就像画家在精雕细琢时,会时不时地退后几步,再次眯眼看看整体效果,确保细节的刻画没有偏离整体构图。
2.2.1.4训练过程
DDPM的关键是训练噪声估计模型,使其预测的噪声
与真实用于破坏的噪声
相近,具体怎么个训练过程呢?
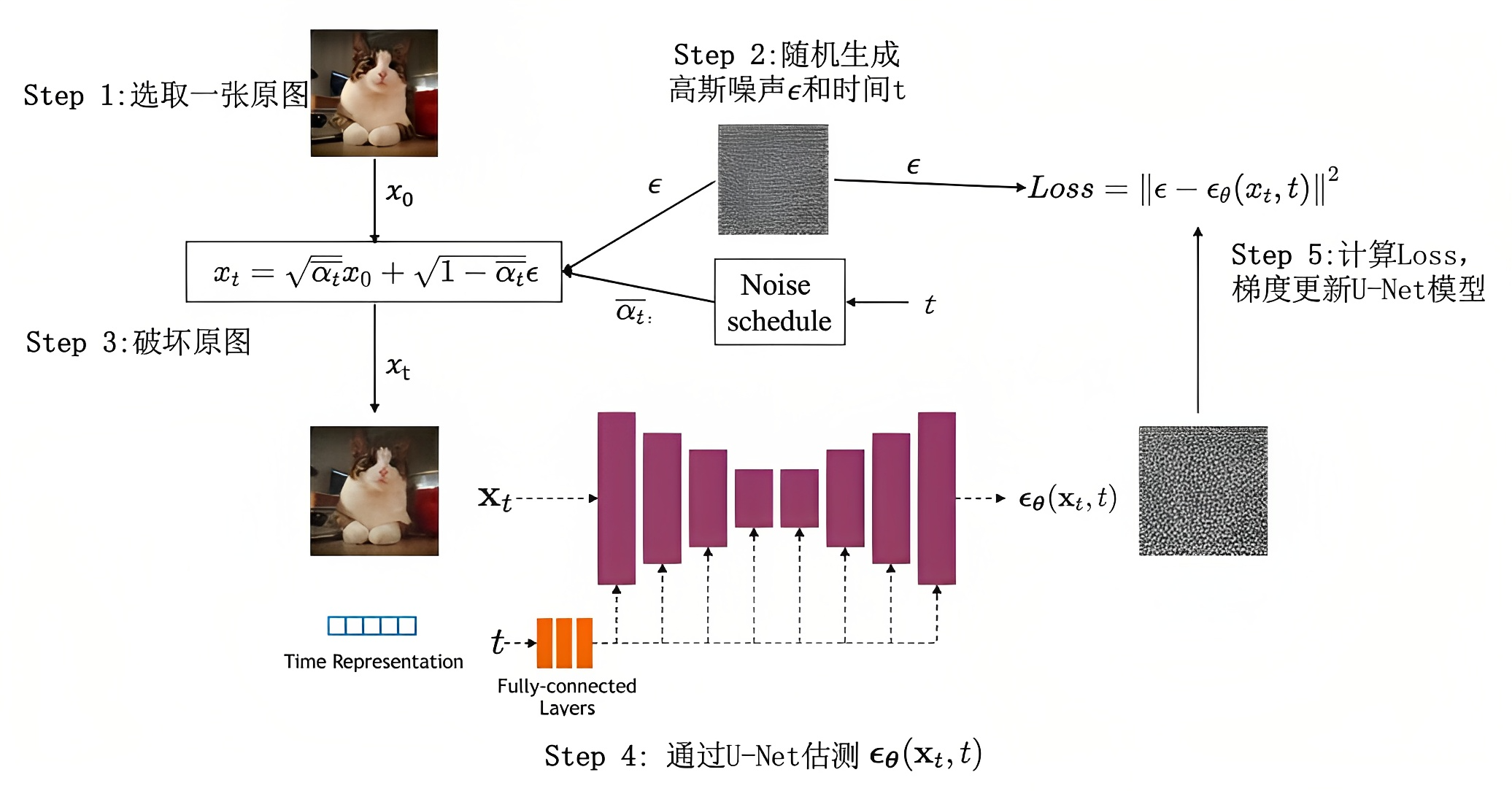
1.选择选择一个训练图像,例如海边沙滩的照片,然后生成随机噪声图像,通过将此噪声图像添加到一定数量的步骤来损坏训练图像
2.然后通过一个噪声估计器U-Net 预测添加的噪声,使其与实际噪声做差异对比,从而建立损失函数做反向传播,最后更新噪声估计器的参数(通过告诉U-Net 我们在每一步添加了多少噪声,从而手把手一步步教U-Net 怎么去估计噪声)
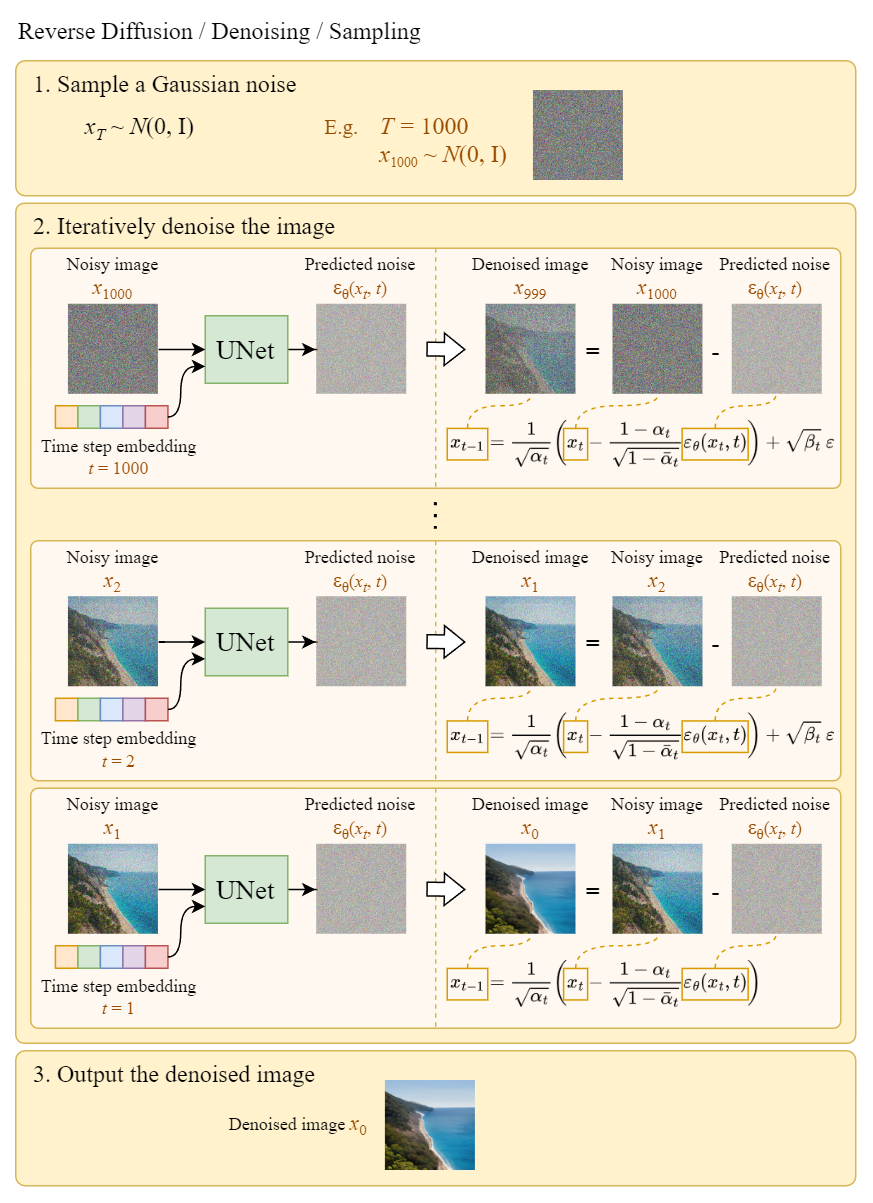
2.2.1.5生成过程
U-Net训练好了之后(意味着其对噪声的估计比较准确了),我们便可以基于训练好的 U-Net 来生成图像。原理很简单,通过噪声估计器预测出噪声后,不模糊的图片便减去每一步添加的噪声以清晰化就可以了。
2.2.2DALL-E 2
DALL-E 2基本就是整合了CLIP和基于扩散模型的GLIDE,而后者则采用了两阶段的训练方式:文本 → 文本特征 → 图片特征 → 图片。
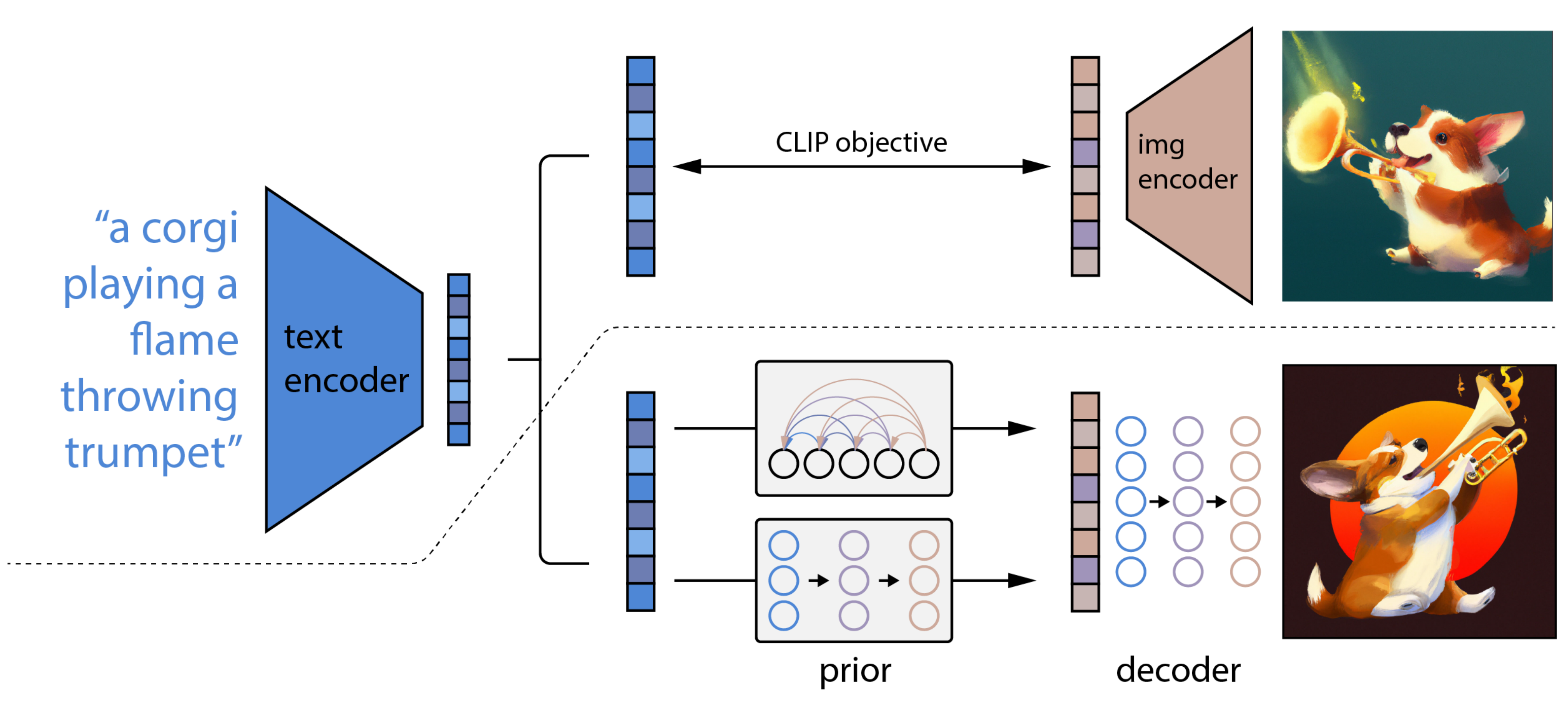
上面的CLIP训练好之后,就将其冻住了,不再参与任何训练和微调,DALL-E2训练时,输入也是文本-图像对,下面就是DALL-E2的两阶段训练:
1.阶段一 prior的训练
根据文本特征(即CLIP text encoder编码后得到的文本特征),预测图像特征(CLIP image encoder编码后得到的图片特征)
实际的训练过程为:将CLIP中训练好的text encoder拿出来,输入文本y,得到文本编码zt。同样的,将CLIP中训练好的img encoder拿出来,输入图像x得到图像编码zi。我们希望prior能从zt获取相对应的zi。假设经过prior输出的特征为zi',那么我们自然希望zi'与zi越接近越好,这样来更新我们的prior模块。最终训练好的prior,将与CLIP的text encoder串联起来,它们可以根据我们的输入文本生成对应的图像编码特征了。
在DALL-E 2 模型中,作者团队尝试了两种先验模型:自回归式Autoregressive (AR) prior 和扩散模型Diffusion prior。实验效果上发现两种模型的性能相似,而因为扩散模型效率较高,因此最终选择了扩散模型作为prior模块。
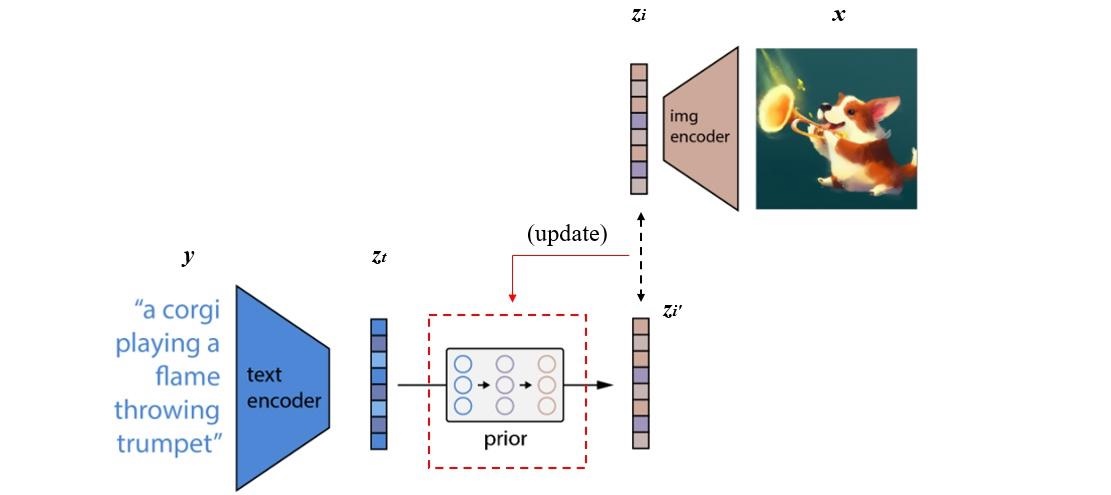
推理时,文本还是通过CLIP text encoder得到文本特征,然后根据训练好的prior得到类似CLIP生成的图片特征,此时图片特征应该训练的非常好,不仅可以用来生成图像,而且和文本联系的非常紧(包含丰富的语义信息)
2.阶段二 decoder生成图
常规的扩散模解码器,解码生成图像。这里的decoder就是升级版的GLIDE(GLIDE基于DDPM模型),所以说DALL-E 2 = CLIP + GLIDE。
2.2.3Stable Diffusion
High-Resolution Image Synthesis with Latent Diffusion Models
Stable Diffusion原来的名字叫“Latent Diffusion Model”(LDM),很明显就是说扩散过程发生隐空间中(即latent space)。
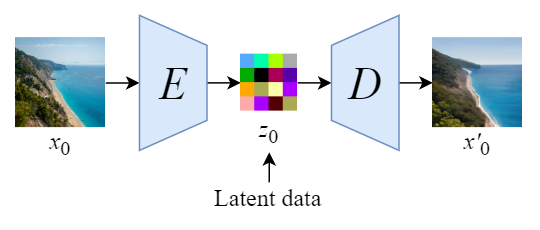
Stable Diffusion会先训练一个自编码器,来学习将图像压缩成低维表示
- 通过训练好的编码器
,可以将原始大小的图像压缩成低维的latent data(图像压缩)
- 通过训练好的解码器
,可以将latent data还原为原始大小的图像
在将图像压缩成latent data后,便可以在latent space中完成扩散过程,对比下和Diffusion扩散过程的区别,如下图所示:
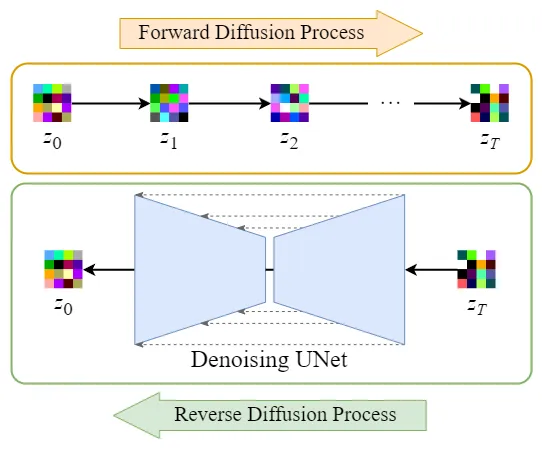
可以看到Diffusion扩散模型就是在原图 上进行的操作,而Stale Diffusion是在压缩后的图像
上进行操作。
那么接下来就可以正式掏出SD的结构图了。
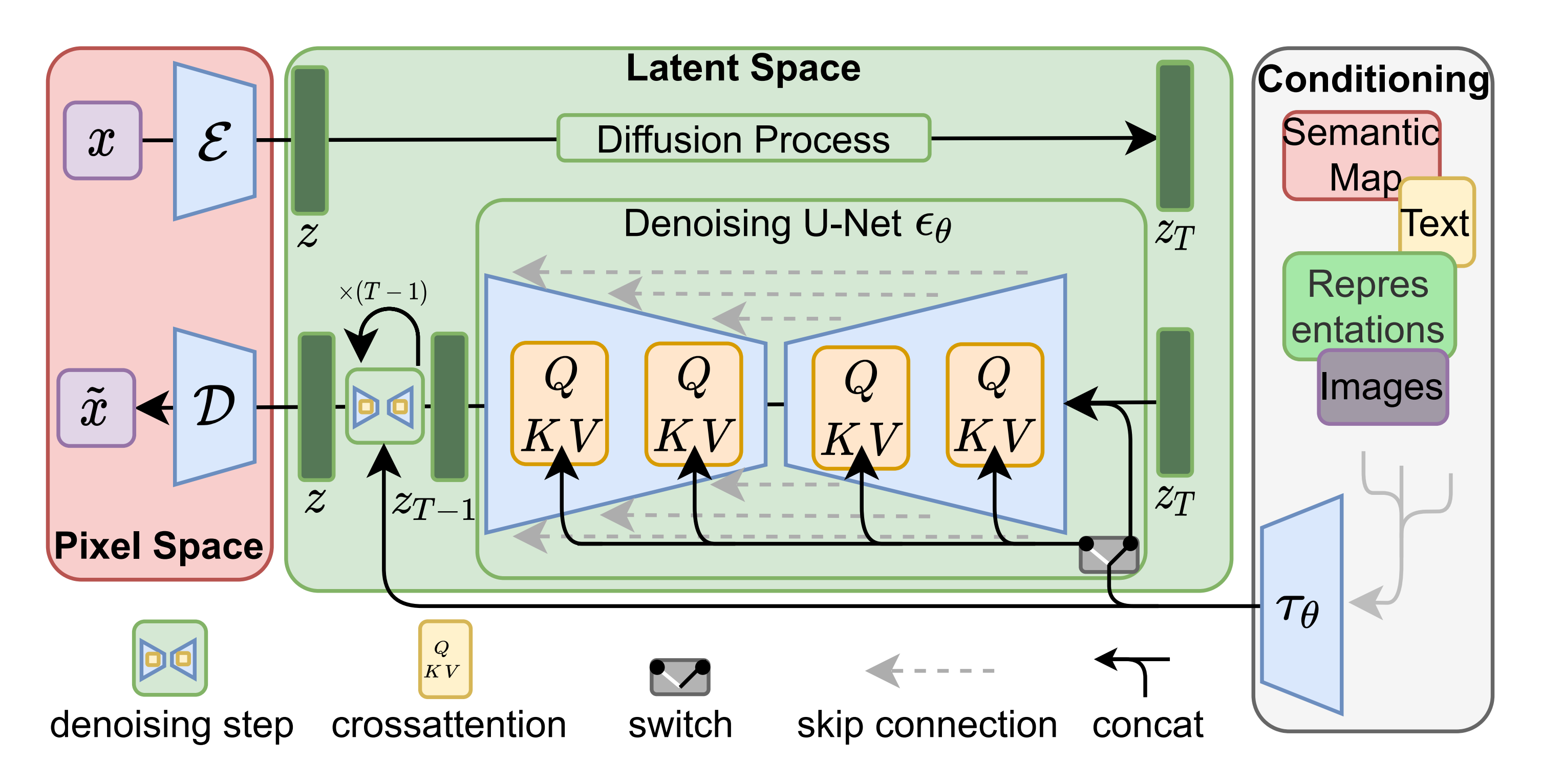
1.将图像从像素空间(Pixel Space)压缩到潜在空间(Latent Space)
图像编码器可以对图像x进行压缩,可以理解为它能忽略图片中的高频信息,只保留重要的深层特征,从而将x从(3, 515, 512)的像素空间压缩到一个维度为(4, 64, 64)的潜在空间
这个就是所谓的感知压缩(Perceptual Compression),即“将高维特征压缩到低维,接着在低维空间上进行操作”的方法具有普适性,可以很容易的推广到文本、音频、视频等不同模态的数据上。
2.针对潜在空间的图片做扩散(Diffusion Process):添加噪声
对潜在空间Latent Space中的图片添加噪声,进行扩散过程,将其结果作为 U-Net 的输入
3.根据用户的输入text/prompt 获取去噪条件(Conditioning)
text encoder提取输入text/prompt的text embeddings(维度为77*768,意味着77个token嵌入向量,其中每个向量包含768个维度)
然后通过cross attention方式送入噪声估计模型UNet中作为去噪条件condition(当然了,去噪时可以灵活地以文本、图像和其他形式为条件,比如以文本为条件即text2img、以图像为条件即 img2img)
比如text2img就用clip,img2img就用ViT,而空间控制信号就是controlnet的核心部分了。
4.噪声估计器U-Net 预测噪声,然后依据「去噪条件」去噪:生成图片的潜在表示
首先,噪声估计器 U-Net 将潜在噪声图像和文本提示作为输入,并预测噪声「该过程也在潜在空间(4x64x64 张量)中」
之后,基于上面第3步的去噪条件对图像通过 噪声估计器U-NET进行去噪(Denoising),以获得生成图片的潜在表示
具体而言,可以分为以下4步骤
a ) 事实上,扩散模型可以理解为一个时序去噪自编码器,我们需要训练使得预测的噪声与真实噪声相近,则目标函数为:
b ) 而在 Latent Diffusion Models 中,引入了预训练的感知压缩模型,它包含一个编码器和一个解码器,这样就可以在训练时利用编码器得到 latent representation,从而让模型在潜在表示空间中学习,其目标函数为:
c ) 对于条件生成任务,我们将拓展为
,这样就可以通过y来控制图片合成的过程,通过在 U-Net 上增加 cross-attention 机制来实现
而为了能够从不同的模态预处理y,论文引入了一个领域专用(不同领域用不同的)编码器,它用来将y映射成一个中间表示(其实就是对不同方式获得的向量进行量化使其符合U-net规格),这样我们就可以很方便的引入各种形式的条件,例如文本、类别、layout等。
d ) 最终模型可通过一个 cross-attention 将去噪条件引导融入到 UNet 中「作为query向量,
作为key和value向量 」,cross-attention 表示为:
其中是 UNet 的一个中间表征
最终,目标函数可以写为:
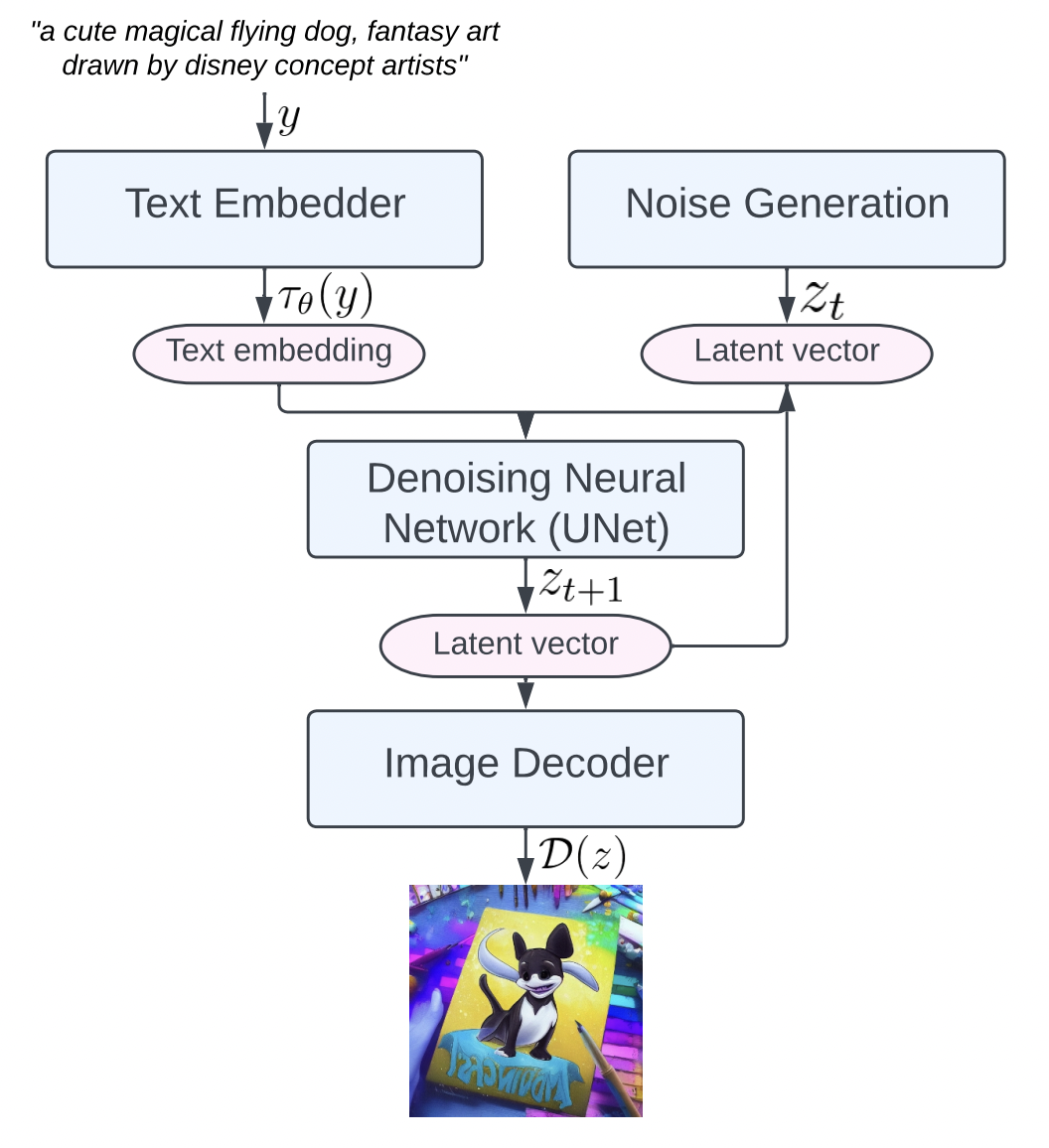
总之,加噪后的隐式表达和文本语义表征通过Attention的方式输入到U-Net,用以更好的学习文本和图像的匹配关系,这里文本的语义向量就是条件(用户的输入text或prompt),控制图像生成往我们想要的方向发展,通过U-Net来预测每一步要减少的噪声。然后计算网络输出噪声和真实噪声的差距,最小化损失来反向传播更新参数(整个训练阶段VAE是冻结的)。
5.潜在空间转换成最终图像
图像解码器负责将去噪后的 latent 图像从潜在空间恢复到原始像素空间来生成最终图「各维度为:(3,512,512),即(红/绿/蓝, 宽, 高)」
2.2.4其他现在的图像生成模型
DALL-E 3用到了consistency-decoder这部分同样比较复杂,涉及较多公式推导,这里就将它的介绍移到公式推导那篇文章中了。
后续Stable Diffusion 3,Flux系列以及其他模型开始使用Diffusion Transformer(DiT,没错还是transformer),而这也是视频生成模型Sora的核心组件。DiT将在视频生成的文章里再进行详细介绍。所以我们对于图像生成模型的探究就暂时止步于次。后面的迭代有机会再单独出文章详细叙述。当然也可以参考下面的链接。这位博主的更新速度以及内容质量都比较高,就是...个人觉得读着比较费劲(排版或者行文风格吧...)。
https://zhuanlan.zhihu.com/p/684068402
2.3现在最新的图像生成模型们
2.3.1 闭源
Imagen 4: https://deepmind.google/models/imagen/ Google Deepmind 2025年5月发布的AI图像生成模型。在LMSYS竞技场T2I子榜上Image 3长期霸榜,Imagen 4生图质量比3高,速度比3快,很可能扩大领先优势。
GPT-4o:2025年4月OpenAI更新的GPT-4o原生的图像生成能力。
DALL·E 3: https://openai.com/dall-e-3 OpenAI研发的AI图像生成器。
Imagine with Meta AI: https://imagine.meta.com/ Meta研发的AI图像生成器,目前免费。
Midjourney: https://www.midjourney.com/ Midjourney研究实验室开发的生图模型,可以实现文字生图和图生图。2025年3月发布v7.0。和Stable Diffusion同时期推出,但是更新太过缓慢,主程序员已离职,不知是否会逐渐式微(用户基础不小)。
快手可图:https://kolors.kuaishou.com/ 快手2025年5月发布的图像生成大模型,最新版为v2.1。
doubao-seedream:https://www.volcengine.com/docs/82379/1555133 字节豆包的图像生成模型,最新版为v3.0。支持原生高分辨率的中英双语图像生成基础模型,响应速度更快,小字生成更准确,文本排版效果增强;指令遵循能力强,美感&结构提升,保真度和细节表现较好。
通义万相(生图):https://tongyi.aliyun.com/wanxiang/creation 阿里通义团队发布的图像生成模型产品,目前模型版本是2025年2月发布的v2.1。支持多种图像生成模板,即将支持图生图。
2.3.2 开源
Flux.1: https://github.com/black-forest-labs/flux 由Stable Diffusion的原班离职人马创立的Black Forrest Lab开发,和SD3一样对硬件的要求偏高。优势是开源后量化和LoRA比较方便。
Stable Diffusion: https://stability.ai/stable-diffusion/ 由CompVis、Stability AI 和 LAION 的研究人员创建文本到图像潜在扩散模型,需下载代码布署本机使用,对电脑硬件配置有一定的要求,目前更新到了3.5版本。
国内目前这部分相当空缺,只有一个HiDream-l1的17B模型,今年4月推出。HiDream-I1: Free HiDream AI Image Generation Online但是影响力并不高。
还有多模态的Janus-pro,由deepseek推出,是一个类似于GPT-4o的多模态大模型。由1B和7B两个量级,今年1月推出。值得注意的一点是这是一个自回归模型。https://huggingface.co/deepseek-ai/Janus-Pro-7B
3.图像生成的未来
3.1 效率革命:走向实时
这个方向的核心是让图像生成更快、更轻量。
案例: InstaFlow: One Step is All You Need for High-Quality Diffusion-Based Text-to-Image Generation
简介: 这篇论文直击扩散模型生成速度慢的核心痛点。它提出了一种名为“InstaFlow”的方法,通过一种名为“精馏”(Rectified Flow)的技术,可以将多步的扩散过程“蒸馏”成单步生成。这意味着用户几乎可以瞬时从文本提示生成高质量图像,极大地提升了生成效率,为实时应用铺平了道路。
3.2 精准到像素级的可控性
这个方向旨在超越简单的文本提示,实现对图像内容、布局、风格、姿态等元素的精细操控。ControlNet 的思想得到了进一步发扬光大。
案例: FLAIR: Fine-grained Language-informed Image Representations
简介: 该研究提出了一种新的视觉语言模型,通过将非常细致的文本描述与图像中的具体区域进行对齐来学习。例如,它不仅仅理解“鸟”,而是能精确对应到“鸟的红色头部”或“伸展的左翼”。这种能力反过来可以用于图像生成,允许用户通过更精细的语言指令来控制生成图像的局部细节。
案例: Mastering Text-to-Image Diffusion Models for Fine-Grained Image Editing
简介: 这篇论文提出了一种新的方法,允许用户对已有图像或生成图像进行非常精细的、区域化的编辑。它能够将用户的文本指令(例如“把这只猫的颜色变成蓝色”)与图像中的特定区域精确对应起来,并进行修改,同时保持图像其他部分不变。这实现了对生成过程更细粒度的控制。
3.3 超越2D:全面拥抱3D
静态图像技术成熟后,学术界的目光大规模转向了更复杂的3D内容和动态视频的生成。
案例 (3D): DreamFusion: Text-to-3D using 2D Diffusion
简介: 尽管 DreamFusion 的核心思想提出稍早,但其深刻影响了 CVPR 2024 的大量后续工作。它开创性地展示了如何利用一个预训练好的2D文本到图像扩散模型(如Imagen),来优化一个神经辐射场(NeRF),从而仅根据文本提示就能生成一个完整的3D模型。你只需要输入“一个穿着宇航服的松鼠”,它就能生成对应的3D模型。
案例: VGGT: Visual Geometry Grounded Transformer
简介: 这篇荣获 CVPR 2025 最佳论文奖的成果,提出了一种可以直接从多个视角估算三维场景属性的前馈神经网络。与需要大量迭代优化的传统方法(如NeRF)相比,VGGT 的前馈特性使其速度极快,为实时3D视觉应用(包括快速3D内容生成和编辑)提供了全新的、高效的架构思路。
3.4 可信度、安全与伦理
案例: Interactive Medical Image Analysis with Concept-based Similarity Reasoning
简介: 这篇论文提出了一种人机交互式的医学影像分析方法。它允许医生通过基于“概念”(如“肿瘤的某种特定纹理”)的相似性推理来引导AI模型进行分析。AI的决策过程不再是一个黑箱,而是可以被医生理解和验证的。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容









所有评论(0)