oi！让我来给你唠唠咋实现红黑树☝️

先旋转在将p变为黑，pp变为红，使其满足规则。这样调整过后p变成了新的”根”节点，且为黑色，而黑色节点不论p的上一层是黑色还是红色都符合规则。所以旋转+变色后就结束调整。（在旋转过程中，因为这里是三叉链要注意_parent指针的更新，详细可参考具体的实现代码）先p点旋转，再pp点旋转，最后cue变黑色 pp变红色。这样调整过后cur变成了新的”根”节点，且为黑色，而黑色节点不论cur的上一层是黑色

huangyuchi.

1100人浏览 · 2025-03-10 21:46:03

huangyuchi. · 2025-03-10 21:46:03 发布

破除高大上的迷雾

可不要被名号吓着了！红黑树其实就是：二叉搜索树+四条红黑树规则的特殊二叉搜索树

红黑树四大规则：
1.红黑树的每一个节点都有且仅有两种颜色：红色与黑色

2.红黑树的根节点一定为黑色

3.对于一个红色节点，其左右孩子一定为黑色

4.对于任意一个节点来说，从这个节点出发到空节点的有所路径中，黑色节点的数量是一定相同的

基础~ 红黑树的结构

对于规则1，我们可以使用enum枚举红和黑，这样会更加便捷、并且不会再颜色分配上出错。然后对于节点类RBTreeNode的实现，我们还是默认使用pair结构实现。同时因为我们会用到找父亲节点的情况，所以我们这里与avl树一样都为三叉链。

这里我们最重要的一个成员变量为_col ，在初始化的时候注意要初始化为红（RED）具体原因我们后面解释

// 枚举值表⽰颜⾊ 
enum Colour
{
	RED,
	BLACK,
};

// 这里我们默认按key/value结构实现 
template<class K, class V>
struct RBTreeNode
{
	// 这⾥更新控制平衡也要加⼊parent指针 
	pair<K, V> _kv;
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	Colour _col;

	RBTreeNode(const pair<K, V>& kv)//const?
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		,_col(RED)
	{}
};

template<class K, class V>
class RBTree
{
	//typedef RBTreeNode<K, V> Node;
	using Node = RBTreeNode<K, V>;
public:

private:
    Node* _root = nullptr;
}

重点~红黑树的插入

红黑树的插入主要分为两大步骤：插入、调整

插入

红黑树的插入的本质与搜索二叉树的插入相同：

1.若树为空，插入的数据为根节点的数据

2.若树不为空，按照二叉搜索树的性质，判断节点的值与插入值的大小关系。若大于节点的值则往右边走。若小于节点的值则往左边走

（抱有疑问的同学可以参考：二叉搜索树的实现（C++）-CSDN博客）

插入颜色：对于插入节点的颜色，我们有红与黑两个选择。如果我们插入黑，就会违反规则4导致一条路径的黑色节点数量增加，而这种情况我们是及难维护的（所以这就是为什么我们一开始就说要初始化为红）。所以我们选择插入红，如果父亲节点为黑则顺利完成插入，如果父亲节点为红，则违反规则3，我们插入之后进行调整（特殊：当然如果插入的节点为根节点，我们则插入黑色节点，因为遵循规则2）

bool Insert(const pair<K, V>& kv)
{
	Node* cur = _root;
	Node* parent = cur;

	if (!cur)//如果是空树
	{
		_root = new Node(kv);
		_root->_col = BLACK;
		return true;
	}

	while(cur)
	{
		if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = parent->_left;
		}
		else if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = parent->_right;
		}
		else
		{
			return false;
		}
	}
	cur = new Node(kv);
	if (parent->_kv.first > kv.first)
		parent->_left = cur;
	else
		parent->_right = cur;

	//连接至上一层
	cur->_parent = parent;

    return true;
}

由于这里我们是三叉链，所以与二叉搜索树不同的处理是，我们最后一步要将插入的节点的parent链接至上一层

调整

在插入节点后判断是否违反了规则3，若违反了则我们来到了这里，进行调整。

（插入节点：cur，简称c cur的父亲：parent，简称p parent的父亲：pparent，简称pp parent的兄弟：uncle，简称 u）

变色

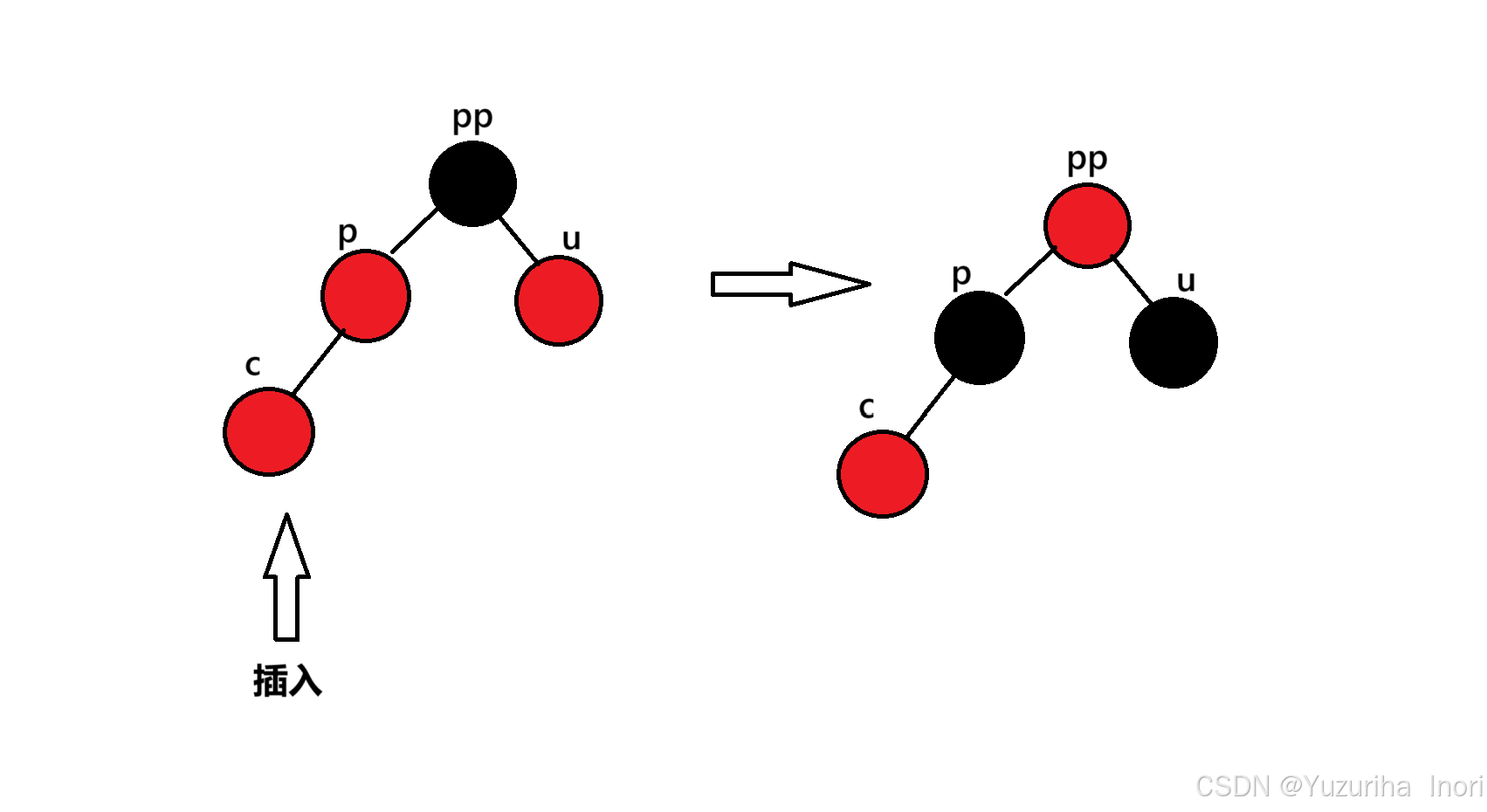
当uncle存在且为红时，我们只需要进行变色操作，就可以让其再次符合规则：

首先，parent是一定要变为黑色，不然无法满足规则3。变为黑色后，不满足规则4，我们直接将pp变为红，u变为黑。这样就完全符合所有规则了

现在可能就有同学问了：为什么不将c变为黑呢？首先c之所以是红，是因为我们在一开始说的一来就插入黑色，我们是极其不好维护的，现在又将c变回去，那岂不是走老路了吗？所有c是不能变的，只能让parent变

总结：当u存在且为红时，p、u变黑，pp变黑
后续处理：此时pp为红，我们需要判断一下pp是否为这颗树的根。若pp此时正好是根，那么将pp再次赋值为黑（满足规则2）结束调整。如果不为空，判断pp的父亲节点是否为红，若不为红结束调整。如果为红则继续向上调整

变色+单旋

当uncle不存在时：

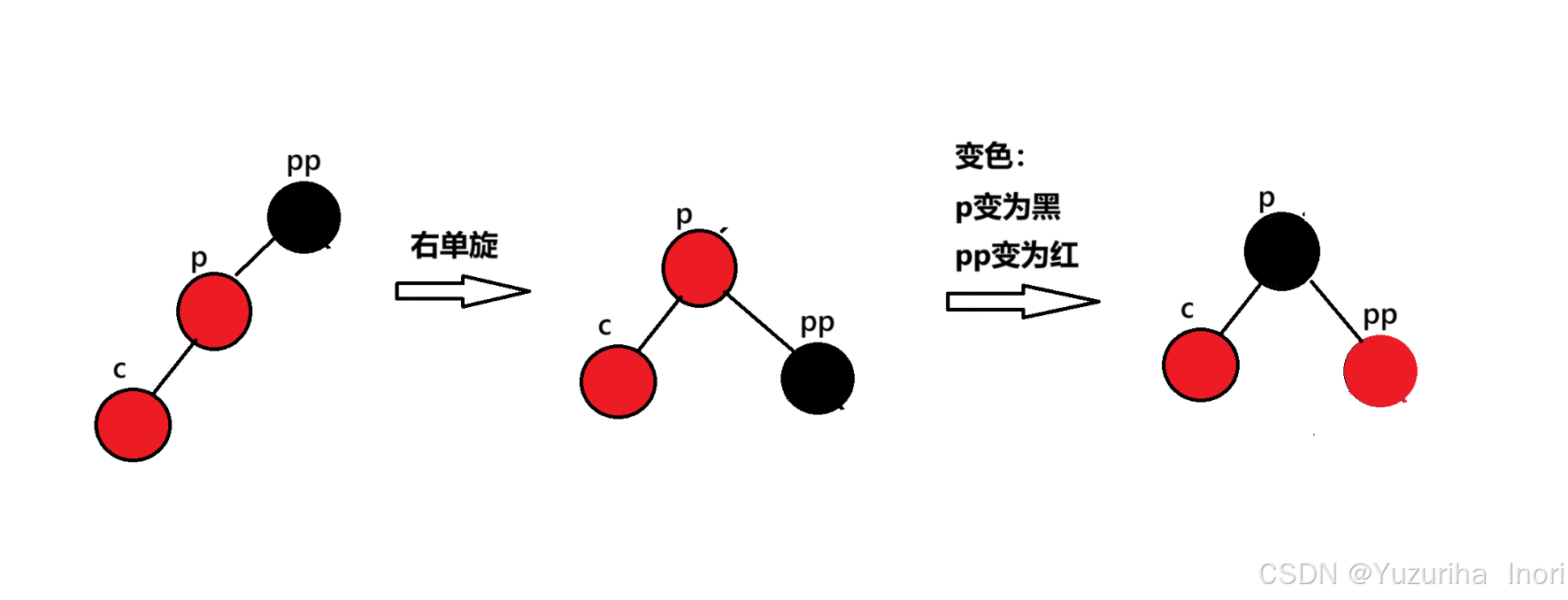
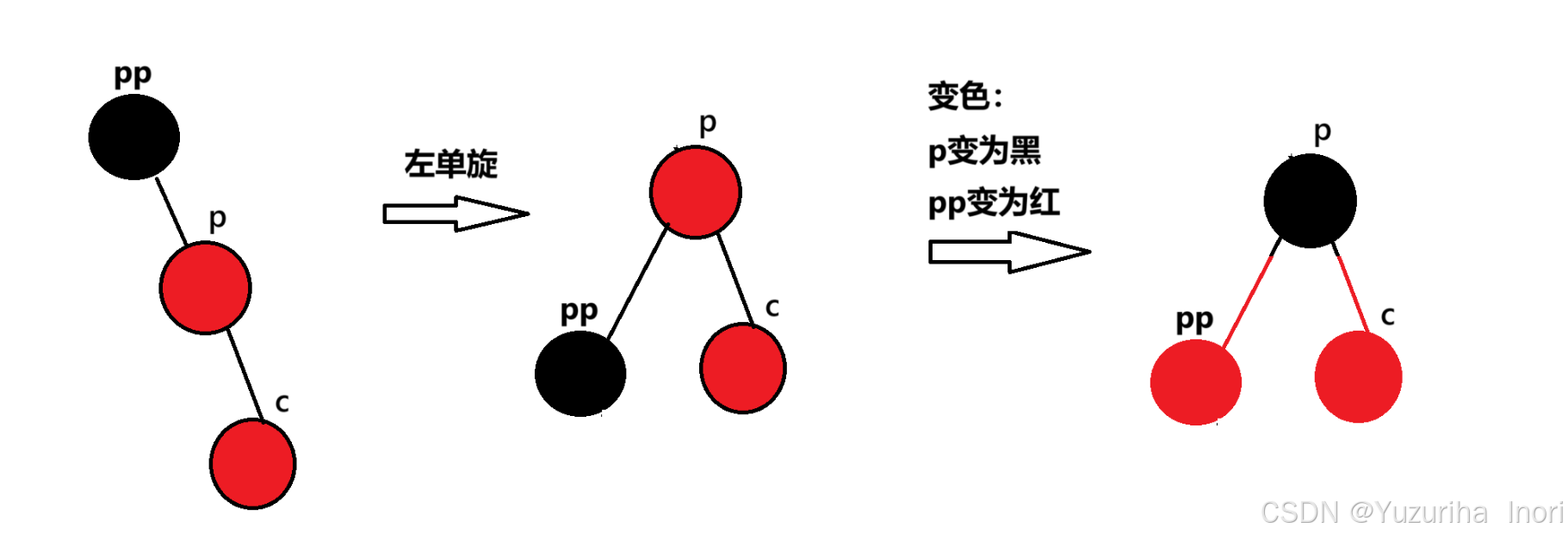
右单旋：让pp变成p的右子树

左单旋：让pp变成p的左子树

这以下情况通过一次旋转+变色，就可以使其再次满足规则，而其他情况则需要双旋+变色

当uncle存在且为黑时：

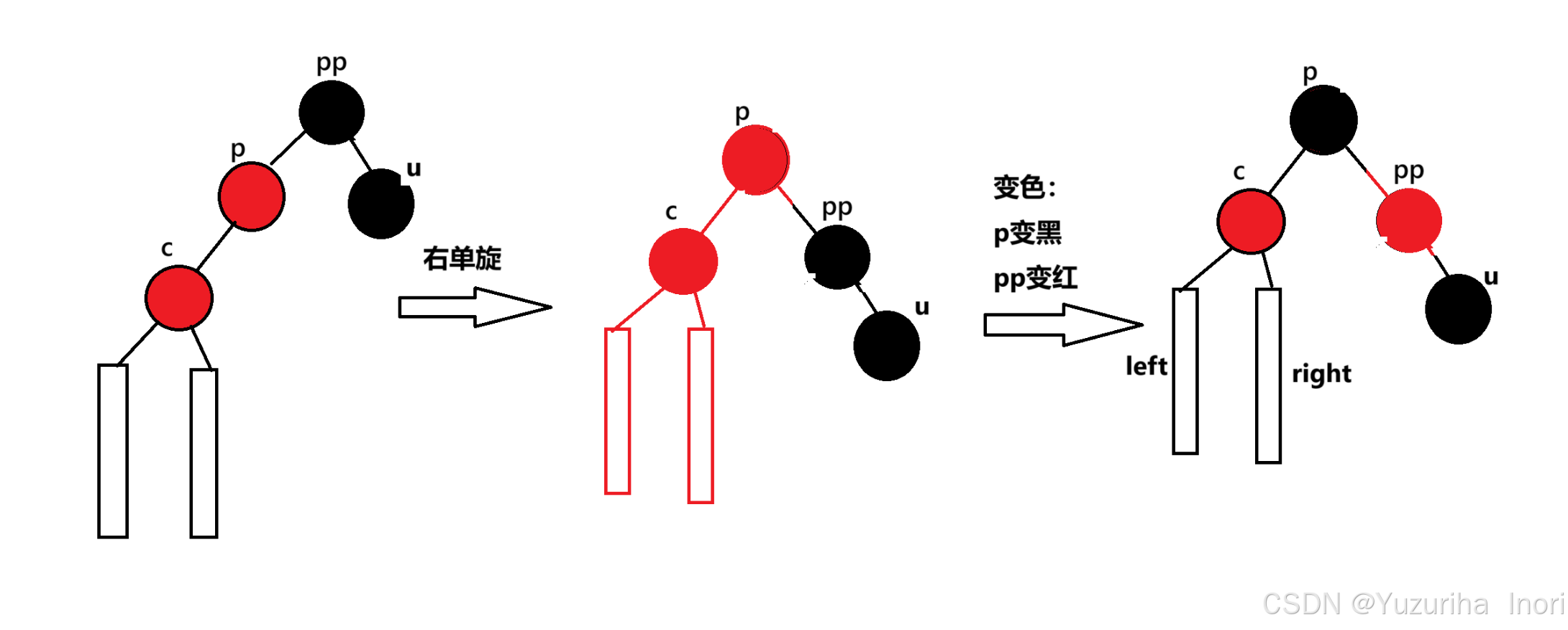大家看这个图的时候可能有点疑惑。怎么感觉最后结果每个路劲的黑色节点数也没有保持一样呢？

这里需要我们考虑一个小细节：那就是cur节点是怎么来的？我先给出结论：cur这个节点一定是之前已经存在且为黑的节点。原因：如果cur是之后插入进来的节点，那么这棵树一开始黑色节点的数量就不一致，这是不可能的。所以cur是之前就存在的节点，既然存在，那么要想使得黑色节点的数量保持一致，那cur之前只能是黑色的。

反过来思考，当uncle不存在时。cur就只能是之后插入进来的。

所以cur是之前存在且为黑的，那它现在变成了红，也就意味着发生了我们最开始讲的变色情况：cur的左右孩子变为黑色，cur变为红色。所以这里的结果看似不符合规则，其实是符合的。

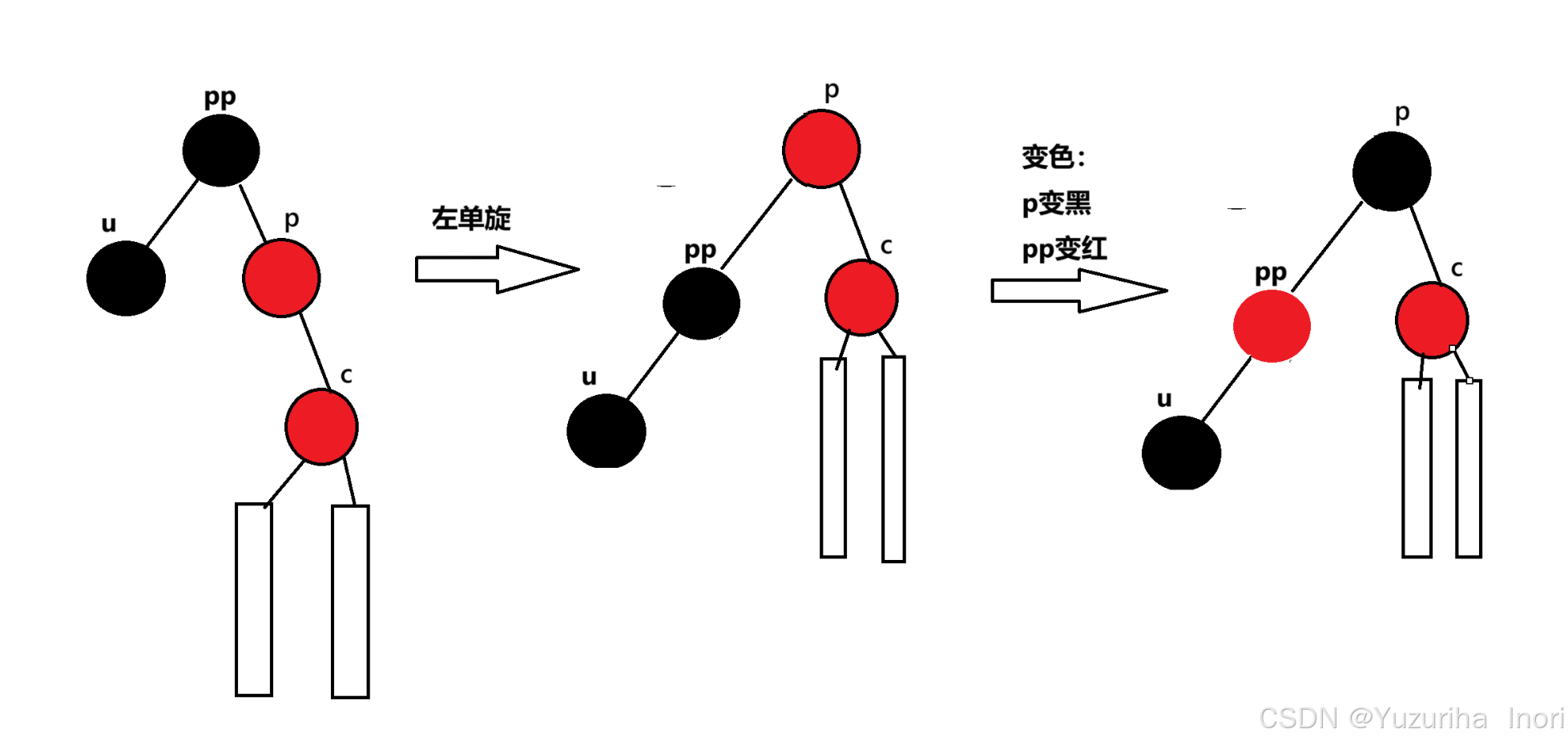
一样的，与上一个同理

总结：

先旋转在将p变为黑，pp变为红，使其满足规则。这样调整过后p变成了新的”根”节点，且为黑色，而黑色节点不论p的上一层是黑色还是红色都符合规则。所以旋转+变色后就结束调整。（在旋转过程中，因为这里是三叉链要注意_parent指针的更新，详细可参考具体的实现代码）

变色+双旋

当uncle不存在时：

以下的四种情况仅仅依靠一次旋转是无法解决的，我们这里使用了两次旋转：左单选和右单选（简称双旋）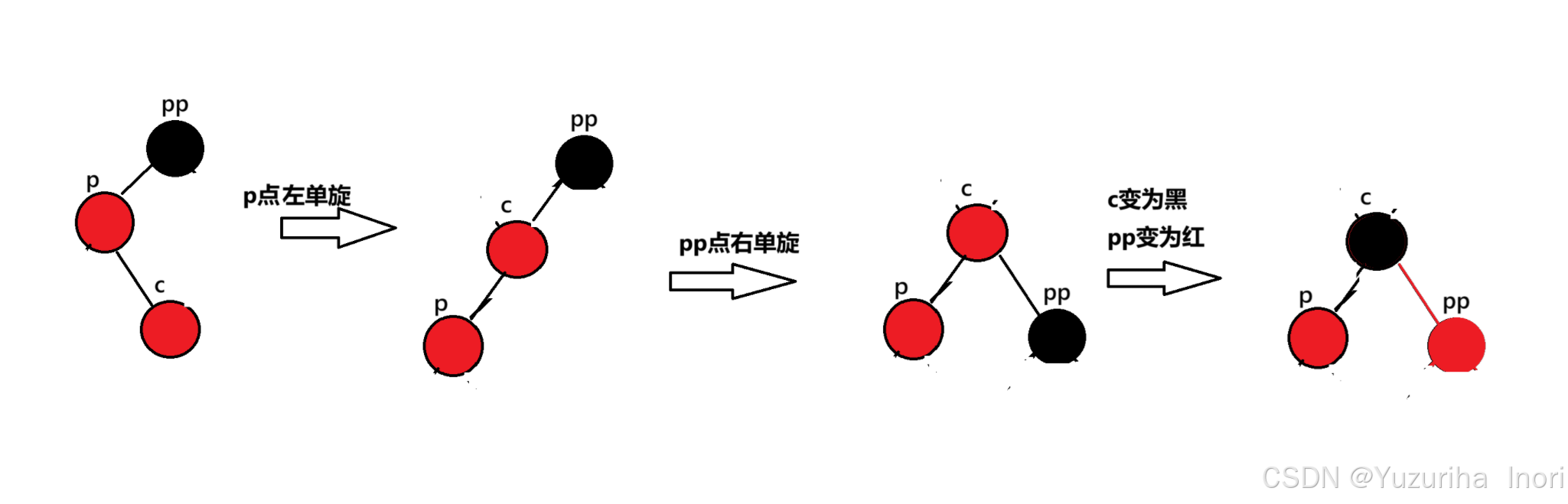

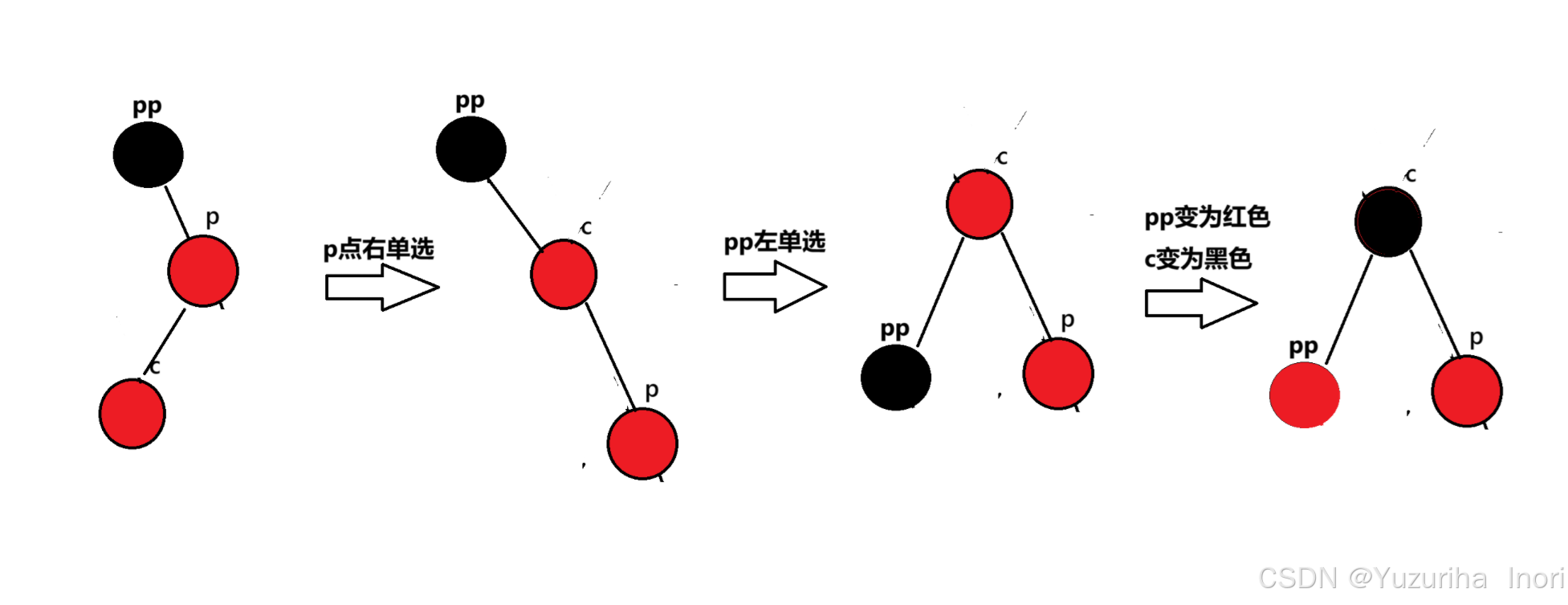
当uncle存在且为黑时：

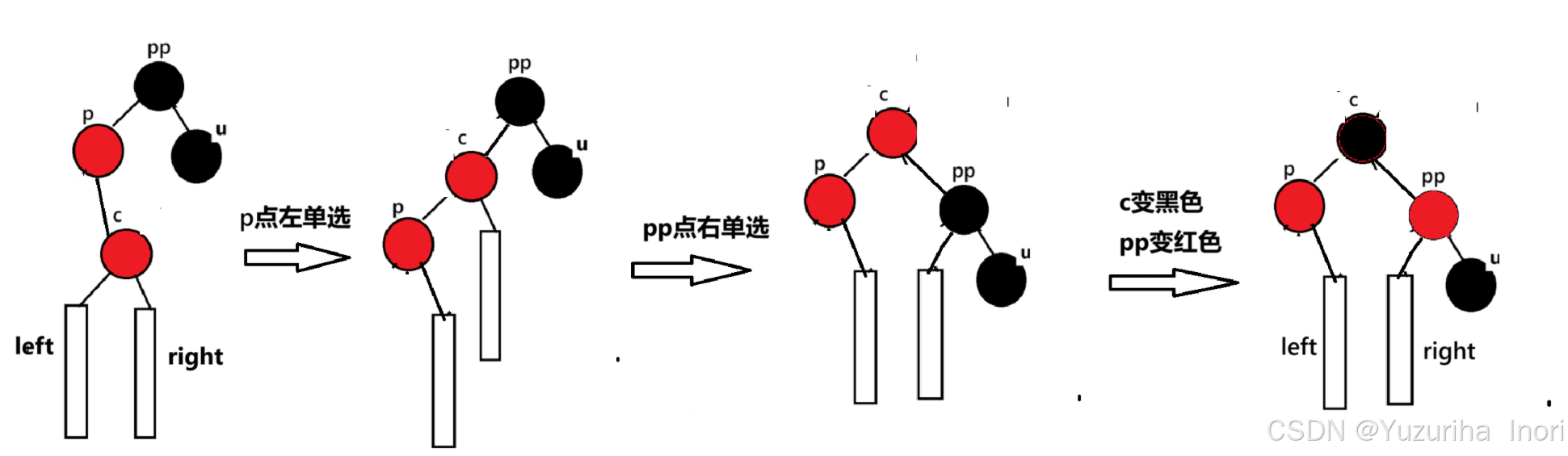这里和单旋是情况一样：cur的之前就已经存在且为黑的点，这里cue变成了红色，而cur的左右孩子变成了黑色。看起来黑色节点是数量不一致，其实是一致的

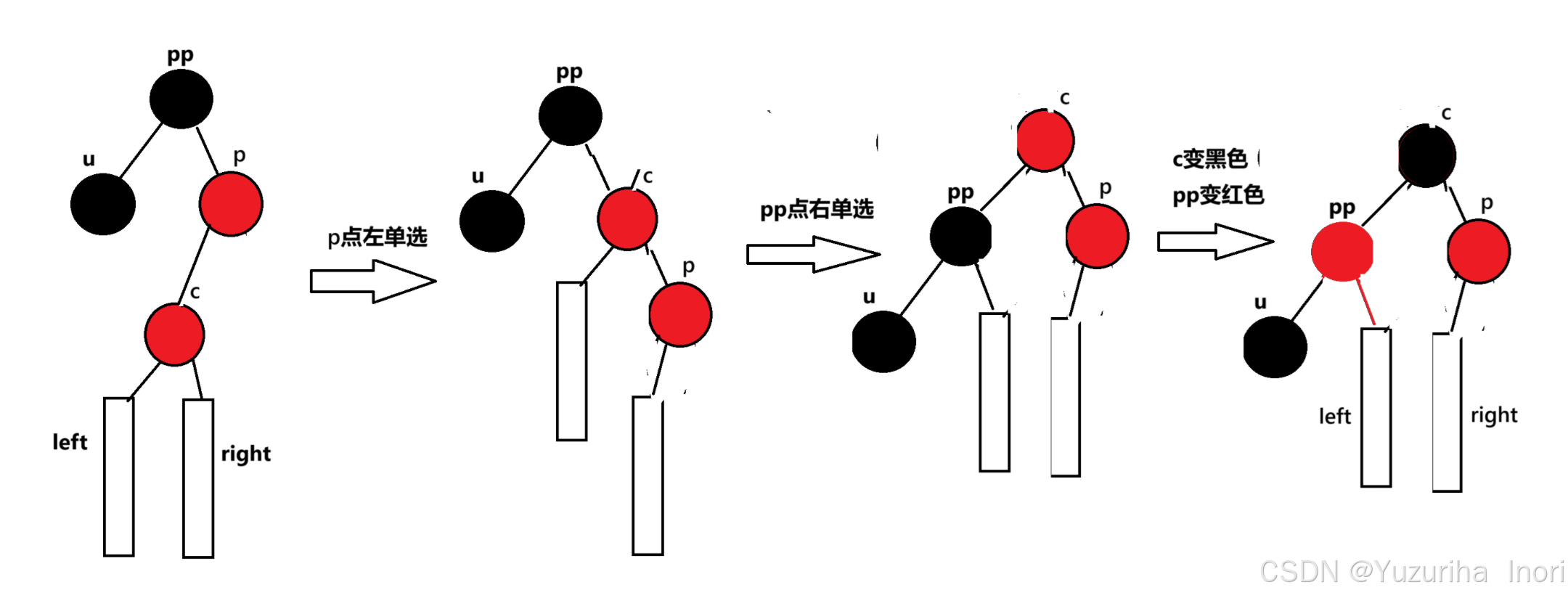
与上同理

总结：

先p点旋转，再pp点旋转，最后cue变黑色 pp变红色。这样调整过后cur变成了新的”根”节点，且为黑色，而黑色节点不论cur的上一层是黑色还是红色都符合规则。所以旋转+变色后就结束调整。（在旋转过程中，因为这里是三叉链要注意_parent指针的更新，详细可参考具体的实现代码）

调整的代码实现

//判断是否满足条件
while (parent&&parent->_col == RED)
{
	Node* pparent = parent->_parent;

	//先讨论parent在左边的情况
	if (pparent->_left == parent)
	{
		Node* uncle = pparent->_right;
		//uncle存在且为红 -> 变色
		if (uncle && uncle->_col == RED)
		{
			parent->_col = uncle->_col = BLACK;
			pparent->_col = RED;

			cur = pparent;
			parent = cur->_parent;
		}
		else
		{
			//单旋+变色
			if (parent->_left == cur)
			{
				RotateR(pparent);
				pparent->_col = RED;
				parent->_col = BLACK;
				break;
			}
			//双旋+变色
			else
			{
				RotateL(parent);
				RotateR(pparent);
				pparent->_col = RED;
				cur->_col = BLACK;
				break;
			}
		}
	}
	else//再讨论parent在右边的情况
	{
		Node* uncle = pparent->_left;
		//uncle存在且为红 -> 变色
		if (uncle && uncle->_col == RED)
		{
			parent->_col = uncle->_col = BLACK;
			pparent->_col = RED;

			cur = pparent;
			parent = cur->_parent;
		}
		else
		{
			//单旋+变色
			if (parent->_right == cur)
			{
				RotateL(pparent);
				parent->_col = BLACK;
				pparent->_col = RED;
				break;
			}
			else//双旋+变色
			{
				RotateR(parent);
				RotateL(pparent);
				cur->_col = BLACK;
				pparent->_col = RED;
				break;
			}
		}
	}
	_root->_col = BLACK;
}

//右单旋
void RotateR(Node* parent)
{
	Node* pparent = parent->_parent;
	Node* subL = parent->_left;
	Node* subLR = subL->_right;

	if(subLR)
		subLR->_parent = parent;
	parent->_left = subLR;
	
	subL->_right = parent;
	parent->_parent = subL;

	if (!pparent)
	{
		_root = subL;
		subL->_parent = nullptr;
	}
	else
	{
		if (pparent->_left == parent)
		{
			subL->_parent = pparent;
			pparent->_left = subL;
		}
		else
		{
			subL->_parent = pparent;
			pparent->_right = subL;
		}
	}
}

//左单旋
void RotateL(Node* parent)
{
	Node* pparent = parent->_parent;
	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	parent->_right = subRL;
	if (subRL)
		subRL->_parent = parent;

	subR->_left = parent;
	parent->_parent = subR;

	if(!pparent)
	{
		_root = subR;
		subR->_parent = nullptr;
	}
	else
	{
		if (pparent->_left == parent)
		{
			pparent->_left = subR;
			subR->_parent = pparent;
		}
		else
		{
			pparent->_right = subR;
			subR->_parent = pparent;
		}
	}
}

对于红黑树验证

1. 规则1：枚举颜色类型，天然实现保证了颜色不是黑色就是红色。

2. 规则2：直接检查根即可。

3. 规则3：前序遍历检查，遇到红色结点查孩子不太方便，因为孩子有两个，且不一定存在，反过来检查父亲的颜色就方便多了。

4. 规则4：前序遍历，遍历过程中用形参记录跟到当前结点的blackNum(黑色结点数量)，前序遍历遇到黑色结点就++blackNum，走到空就计算出了一条路径的黑色结点数量。再任意一条路径黑色结点数量作为参考值，依次比较即可。

//检查红黑树是否满足要求
bool Check(Node* root, int blacknum,int refNum)
{
	if (!root)
	{
		if (blacknum != refNum)
		{
			cout << "存在黑色节点不一致的路径";
			return false;
		}
		return true;
	}

	int num = blacknum;
	//检查根
	if (root == _root && _root->_col != BLACK)
		return false;
	
	//前序遍历验证：黑色节点数以及红色节点的孩子
	if (root->_col == RED && root->_parent->_col == RED)
	{
		cout << "出现连续红色节点";
		return false;
	}
	if (root->_col == BLACK)
	{
		num++;
	}

	return Check(root->_left, num,refNum) && Check(root->_right, num, refNum);
}

bool IsBalance()
{
	if (_root == nullptr)
		return true;
	if (_root->_col == RED)
		return false;

	// 参考值 
	int refNum = 0;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_col == BLACK)
		{
			++refNum;
		}
		cur = cur->_left;
	}
	return Check(_root, 0, refNum);
}

红黑树代码实现

//红黑树：二叉搜索树+4条红黑树规则
// 1.红黑树所有节点有且只有两种颜色：红、黑
// 2.红黑树的根必须为黑色
// 3.红色节点的孩子必须为黑色
// 4.对于任意一个节点，从这个节点开始到NULL节点的黑色节点数量都是一样的


// 枚举值表⽰颜⾊ 
enum Colour
{
	RED,
	BLACK,
};

// 这里我们默认按key/value结构实现 
template<class K, class V>
struct RBTreeNode
{
	// 这⾥更新控制平衡也要加⼊parent指针 
	pair<K, V> _kv;
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	Colour _col;

	RBTreeNode(const pair<K, V>& kv)//const?
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		,_col(RED)
	{}
};

template<class K, class V>
class RBTree
{
	//typedef RBTreeNode<K, V> Node;
	using Node = RBTreeNode<K, V>;
public:

	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < key)
			{
				cur = cur->_right;
			}
			else if (cur->_kv.first > key)
			{
				cur = cur->_left;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}


	bool Insert(const pair<K, V>& kv)
	{
		Node* cur = _root;
		Node* parent = cur;

		if (!cur)//如果是空树
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}

		while(cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = parent->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = parent->_right;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first > kv.first)
			parent->_left = cur;
		else
			parent->_right = cur;

		//连接至上一层
		cur->_parent = parent;


		//判断是否满足条件
		while (parent&&parent->_col == RED)
		{
			Node* pparent = parent->_parent;

			//先讨论parent在左边的情况
			if (pparent->_left == parent)
			{
				Node* uncle = pparent->_right;
				//uncle存在且为红 -> 变色
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					pparent->_col = RED;

					cur = pparent;
					parent = cur->_parent;
				}
				else
				{
					//单旋+变色
					if (parent->_left == cur)
					{
						RotateR(pparent);
						pparent->_col = RED;
						parent->_col = BLACK;
						break;
					}
					//双旋+变色
					else
					{
						RotateL(parent);
						RotateR(pparent);
						pparent->_col = RED;
						cur->_col = BLACK;
						break;
					}
				}
			}
			else//再讨论parent在右边的情况
			{
				Node* uncle = pparent->_left;
				//uncle存在且为红 -> 变色
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					pparent->_col = RED;

					cur = pparent;
					parent = cur->_parent;
				}
				else
				{
					//单旋+变色
					if (parent->_right == cur)
					{
						RotateL(pparent);
						parent->_col = BLACK;
						pparent->_col = RED;
						break;
					}
					else//双旋+变色
					{
						RotateR(parent);
						RotateL(pparent);
						cur->_col = BLACK;
						pparent->_col = RED;
						break;
					}
				}
			}
			_root->_col = BLACK;
		}
		return true;
	}

	//右单旋
	void RotateR(Node* parent)
	{
		Node* pparent = parent->_parent;
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		if(subLR)
			subLR->_parent = parent;
		parent->_left = subLR;
		
		subL->_right = parent;
		parent->_parent = subL;

		if (!pparent)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (pparent->_left == parent)
			{
				subL->_parent = pparent;
				pparent->_left = subL;
			}
			else
			{
				subL->_parent = pparent;
				pparent->_right = subL;
			}
		}
	}

	//左单旋
	void RotateL(Node* parent)
	{
		Node* pparent = parent->_parent;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;

		subR->_left = parent;
		parent->_parent = subR;

		if(!pparent)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (pparent->_left == parent)
			{
				pparent->_left = subR;
				subR->_parent = pparent;
			}
			else
			{
				pparent->_right = subR;
				subR->_parent = pparent;
			}
		}
	}

	//检查红黑树是否满足要求
	bool Check(Node* root, int blacknum,int refNum)
	{
		if (!root)
		{
			if (blacknum != refNum)
			{
				cout << "存在黑色节点不一致的路径";
				return false;
			}
			return true;
		}

		int num = blacknum;
		//检查根
		if (root == _root && _root->_col != BLACK)
			return false;
		
		//前序遍历验证：黑色节点数以及红色节点的孩子
		if (root->_col == RED && root->_parent->_col == RED)
		{
			cout << "出现连续红色节点";
			return false;
		}
		if (root->_col == BLACK)
		{
			num++;
		}

		return Check(root->_left, num,refNum) && Check(root->_right, num, refNum);
	}

	bool IsBalance()
	{
		if (_root == nullptr)
			return true;
		if (_root->_col == RED)
			return false;

		// 参考值 
		int refNum = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
			{
				++refNum;
			}
			cur = cur->_left;
		}
		return Check(_root, 0, refNum);
	}


private:
	

	Node* _root = nullptr;
};

以上结束本文的内容了，感谢大家，我们下期再见！如有问题还请各位大佬斧正