目的：将三相交流量转化成了两相直流量，方便我们用比例积分或者其他的控制算法去控制 

对于三相对称交流电，以三相电压为例进行说明，

首先介绍欧拉公式 

 其θ角可以表示某正弦量所处的空间位置，此公式可看做一个单位矢量，主要反映角度关系，某一个矢量和相乘就表示空间位置逆时针旋转了θ角度。

一、3/2变换，即clark变换 

把三相电压表达式放在三相ABC坐标系中，电压每相相差120度，如果把A轴对应的θ角定为0度，则A,B,C三相坐标系上的正弦矢量可分别表示如下，

相当于ua在A轴上，ub在B轴上，uc在C轴上。

则合成矢量表达式如下： 

上面最后式子相当于一个在实轴上，一个在虚轴上，虚轴超前于实轴90度。这样原来三个方向上的量就可以用两个方向的量来表示。即从ABC坐标系转换到坐标系。换种方式表达如下：

Vα,Vβ即为两相静止坐标系下的分量，对应坐标系如下图所示：

将式1中的三相电压表达式代入上式：

 由运算结果可得，Vα超前于Vβ 90度，两者幅值相等。但幅值为原来式1中三相电压的3/2倍。

（1）下面采用等幅值变换 ，将原表达式×2/3

此时得到的新的α轴，β轴分量的表达式如下：

这样坐标变换矩阵就如下所示：

其中最后一行均为1/2，是因为它包含了不对称三相正弦量的情况，此时就会多出来一个零轴分量 因为我们主要研究的是三相对称电路，不必纠结。

再将式（1）的三相电压代入上式：

 可得经过等幅值变换后的合成矢量的幅值为：

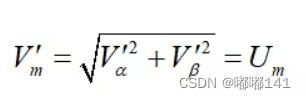
经过等幅值变换后合成矢量的幅值就是原来给定三相电压的幅值，这样变化前后，三相ABC坐标系和两相αβ静止坐标系上的正弦量幅值均相等。

（2）等功率变换 

 如果设三相电压与电流的夹角为 θ，那么变换到两相坐标系后，电压电流的夹角依然不变。

则三相平均有功功率可表示为： 

 两相αβ坐标系下对应的有功功率可表示为： 

假设原来变换时，乘以个系数k，使得前后功率相等，则相当于变换后电压电流都多了个系数k，

得k=

最终变换为：

二、Park变换

      旋转变换，由两相静止坐标系到两相旋转坐标系上的转化，旋转角度与三相正弦量的角度一致。从A轴开始，以wt的角速度旋转，这样合成的电压矢量会和dq0坐标轴同步旋转，旋转矢量和旋转的dq0坐标系处于一个相对静止的状态，所以坐标轴上的分量就是直流量了，这样就把三相交流量转化成了两相直流量，方便我们用算法去控制 。

具体的转换过程如下：

1. 根据αβ坐标系下的信号，得到信号与dq坐标系下的信号之间的夹角θ。
2. 根据夹角θ，计算出Park变换矩阵的元素值。
3. 将αβ坐标系下的信号向量通过Park变换矩阵进行矩阵乘法运算，得到dq坐标系下的直流电压和电流分量。

以d轴做主轴的情况为例分析：基于cos的park变换 

通过坐标分解，就是将αβ0坐标系上合成的矢量，分别投影到旋转坐标系的d轴和q轴上，可得：

 将clark变换的公式代入上式就可以得到ABC到dq0的坐标变换矩阵，以等幅值为例，如下：

然后将三相cos形式电压表达式代入：

可以得到：Vd==1, Vq == 0; 此时d是主控轴， 给定cos信号时使得d轴分量为1，所以是基于cos型的坐标系。 

我们习惯把d轴当做主轴来控制，就是通过变换后最好让d轴分量为1，所以当系统所使用的电压为cos形式时，那么用a轴与d轴重合的形式比较方便，此时d轴为1，对应simulink中的Rotating frame aligned with A axis at t = 0模式；如果系统使用的三相为sin的形式，那么使用d初始时刻滞后于a轴90度时比较方便，此时d轴为1。

三、结论

以d轴初始时滞后a轴90度的情况为例：来自：

来自：彻底搞懂电力电子中的坐标变换_哔哩哔哩_bilibili

      通过dq变换后，三相交流电被转换为直流电，这样就使得电力电子设备更容易控制。因为直流电的控制更加简单和灵活，可以通过调节电压和电流来实现精确的控制。同时，dq变换后的直流电可以更容易地进行功率控制、频率控制和相位控制，从而实现对电力系统的精确控制。