【三分钟】熟练使用np.interp函数函数（干货！！！）

迎南而上

8114人浏览 · 2023-12-05 12:10:43

迎南而上 · 2023-12-05 12:10:43 发布

🌵文章目录🌵

🌳引言🌳

在数据处理和科学计算中，我们经常需要根据一组已知的数据点进行插值，以获取未知点的近似值。NumPy库中的np.interp函数是一个非常强大且易于使用的工具，它可以帮助我们快速实现一维线性插值。具体来说，如果已知xp和yp，并且xp和yp具有确定的对应关系(比如yp=sin(xp))，那么对于新的一维数组x，可通过np.interp函数得到数组y，y是基于 xp和yp的映射关系 通过【线性插值】得到的。本文将通过示例代码和详细注释，向大家介绍如何在三分钟内熟练使用np.interp函数。

🌳np.interp函数的基本用法🌳

np.interp函数的基本语法如下：

np.interp(x, xp, fp, left=None, right=None, period=None)

参数说明：

x：需要进行插值的点，可以是一个数或者一个数组。
xp：已知数据点的x坐标，必须是一个递增的数组。
fp：已知数据点的y坐标，与xp长度相同。
left：可选参数，指定当x < xp[0]时的返回值。
right：可选参数，指定当x > xp[-1]时的返回值。
period：可选参数，指定数据的周期。

下面是一个简单的示例：

import numpy as np

# 已知数据点
xp = np.array([0, 1, 2, 3])
fp = np.array([0, 1, 4, 9])

# 需要进行插值的点
x = 1.5

# 使用np.interp进行插值
result = np.interp(x, xp, fp)
print(result)  # 输出：2.5

在这个示例中，我们有一组已知的数据点(0, 0), (1, 1), (2, 4), (3, 9)，我们想要找到x=1.5处的近似值。使用np.interp函数，我们可以轻松地得到结果2.5。

🌳使用left和right参数处理边界情况🌳

当插值点超出已知数据点的范围时，我们可以使用left和right参数来指定返回值。下面是一个示例：

import numpy as np

# 已知数据点
xp = np.array([0, 1, 2, 3])
fp = np.array([0, 1, 4, 9])

# 需要进行插值的点（超出已知数据点范围）
x = -1

# 使用np.interp进行插值，并指定left和right参数
result = np.interp(x, xp, fp, left=-1, right=16)
print(result)  # 输出：-1（因为x < xp[0]，所以返回left参数的值）

在这个示例中，我们指定了left=-1和right=16，所以当x < xp[0]时，返回值为-1；当x > xp[-1]时，返回值为16。

🌳使用period参数处理周期性数据🌳

如果数据是周期性的，我们可以使用period参数来指定周期。下面是一个示例：

import numpy as np

# 已知数据点（周期性数据）
xp = np.array([0, 1, 2, 3])
fp = np.array([0, 1, 4, 9])
period = 4  # 数据周期为4

# 需要进行插值的点（超出已知数据点范围）
x = 5  # 实际等效于x=1（因为5 mod 4 = 1）

# 使用np.interp进行插值，并指定period参数
result = np.interp(x, xp, fp, period=period)
print(result)  # 输出：1（因为x等效于1，所以返回fp[1]的值）

🌳使用场景举例(可视化说明)🌳

示例代码

import numpy as np

# 初始化一维数组xp
xp = np.linspace(0, 10, 20)  # 从[0,10]这个范围等间隔取20个值
# 基于正弦函数对【离散】输入xp生成数组fp
fp = np.sin(xp) # fp = sin(xp)

# 生成一批新的输入
x = np.linspace(0, 10, 100) # 从[0,10]这个范围等间隔取100个值
# 基于离散数组xp和fp的映射关系(正弦函数)，对新的输入数组x预测对应的输出y(线性插值)
y = np.interp(x, xp, fp)

# 绘制图像
import matplotlib.pyplot as plt
plt.axis("off")
plt.plot(xp, fp, 'o', markersize=10) # 原数组 xp fp均已知
plt.plot(x, y, 's', markersize=3) # 新数组 x已知，y是基于 xp与fp的映射关系 通过【线性插值】得到
plt.show()

运行结果
在这里插入图片描述
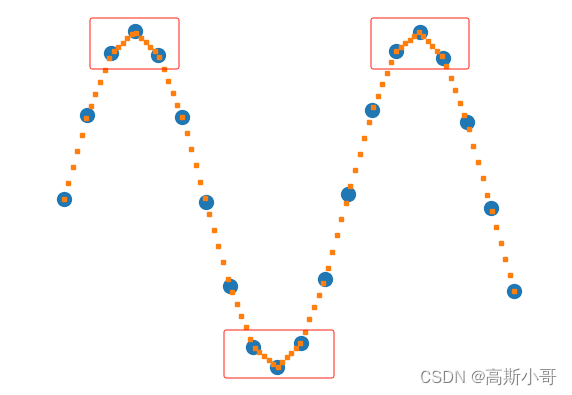
其中，原数组对(xp, yp)用蓝色圆点标记。很明显，(xp, yp)就是sin函数的离散采样点。而新数组(x, y)用橙色正方形标记。可以从上图红色框部分看出，y是基于xp与fp的映射关系通过【线性插值】得到的。

Numpy中文文档

🌳结尾🌳

亲爱的读者，首先感谢您抽出宝贵的时间来阅读我们的博客。我们真诚地欢迎您留下评论和意见💬。
俗话说，当局者迷，旁观者清。您的客观视角对于我们发现博文的不足、提升内容质量起着不可替代的作用。
如果博文给您带来了些许帮助，那么，希望您能为我们点个免费的赞👍👍/收藏👇👇，您的支持和鼓励👏👏是我们持续创作✍️✍️的动力。
我们会持续努力创作✍️✍️，并不断优化博文质量👨‍💻👨‍💻，只为给您带来更佳的阅读体验。
如果您有任何疑问或建议，请随时在评论区留言，我们将竭诚为你解答~
愿我们共同成长🌱🌳，共享智慧的果实🍎🍏！