基于Autoencoder自编码器的数据特征提取和分类

基于自编码器的特征提取主要是通过编码器将输入数据映射到低维空间，这个低维空间可以更好地表示数据的特征。基于自编码器的数据特征提取和分类是一种非常有效的深度学习方法，它可以被广泛应用于各种任务中，例如数据降维、异常检测、数据可视化、语音识别等。自编码器的学习过程是通过最大化重构误差的最小值来实现的，即尽可能减小原始数据与重构数据之间的差异。在基于自编码器的分类任务中，我们通常会训练一个额外的分类器，

fpga和matlab

3183人浏览 · 2023-09-24 00:26:09

fpga和matlab · 2023-09-24 00:26:09 发布

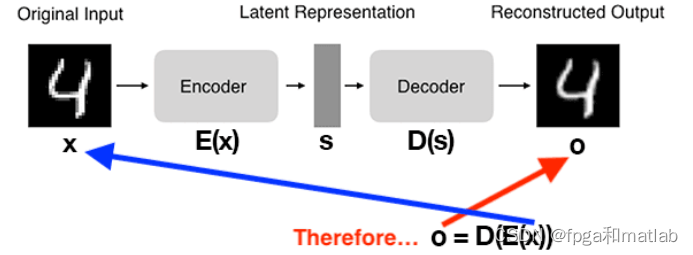
自编码器（Autoencoder）是一种深度学习算法，其主要目标是通过学习将输入数据编码为低维的表示，然后使用这个表示重新构造原始数据。这种算法中的关键思想是，好的编码应该能够通过这个编码和解码的过程保留尽可能多的原始数据信息。其基本结构如下：

基于自编码器的数据特征提取和分类主要利用了自编码器的学习能力和特征提取能力，下面将介绍其原理和数学公式。

一、Autoencoder原理

自编码器由两部分组成：编码器和解码器。编码器将输入数据压缩到一个低维的表示，解码器则从这个低维的表示中恢复出原始数据。自编码器的学习过程是通过最大化重构误差的最小值来实现的，即尽可能减小原始数据与重构数据之间的差异。

基于自编码器的特征提取主要是通过编码器将输入数据映射到低维空间，这个低维空间可以更好地表示数据的特征。然后，解码器利用这个特征表示进行数据重构，以保留更多的原始数据信息。分类任务则需要对编码器的输出进行分类，这可以通过训练一个额外的分类器来完成，例如softmax分类器。在这个情况下，自编码器可以视为特征提取器，用于从原始数据中提取有意义的特征，然后这些特征被用于训练分类器。

假设我们的输入数据为X，编码器函数为f，解码器函数为g，重构误差为重建_error，则自编码器的损失函数可以定义为：

error = E[||X - g(f(X))||_2^2]

其中E[||X - g(f(X))||_2^2]表示对所有输入数据进行上述计算的期望值。

为了优化上述损失函数，我们可以使用梯度下降法或者变分推断进行优化。其中，基于梯度下降法的自编码器可以被表示为：

f, g = argmin_f, g E[||X - g(f(X))||_2^2]

使用变分推断进行优化的自编码器可以被表示为：

f, g = argmin_f, g E[logP(X|f(X))]

其中P(X|f(X))表示给定编码后的表示f(X)重构出原始数据的概率。

在基于自编码器的分类任务中，我们通常会训练一个额外的分类器，例如softmax分类器，来对编码器的输出进行分类。这种情况下，我们的损失函数可以被定义为：

classification_error = E[C(f(X), Y)] + E[||X - g(f(X))||_2^2]

其中C(f(X), Y)表示基于编码表示f(X)和真实标签Y的分类错误率。这样我们就将自编码器的重构误差和分类错误率结合在了一起，可以通过梯度下降或者变分推断进行优化。

基于自编码器的数据特征提取和分类是一种非常有效的深度学习方法，它可以被广泛应用于各种任务中，例如数据降维、异常检测、数据可视化、语音识别等。同时，自编码器还可以和其他算法结合使用，例如卷积神经网络、循环神经网络等，以实现更复杂的功能。

二、Autoencoder的应用

自动编码器在各个领域都有广泛的应用，包括：

降维

自动编码器可以通过学习潜在空间中的紧凑而有效的表示来降低输入数据的维数。这对于可视化、数据压缩和加速其他机器学习算法很有帮助。

特征学习

自动编码器可以从输入数据中学习有意义的特征，这些特征可用于下游机器学习任务，如分类、聚类或回归。

异常检测

通过在普通数据实例上训练自动编码器，它可以学习以低错误重建这些实例。当呈现异常数据点时，自动编码器可能会有更高的重建误差，可用于识别异常值或异常值。

图像降噪

可以训练自动编码器从嘈杂的版本重建干净的输入数据。降噪自动编码器学习消除噪声并生成输入数据的干净版本。

三、MATLAB程序

.....................................................................
%在此处定义时期的数量
for epoch= 1:1:1500
    epoch
    J_epoch=[];Total_Activation = zeros(HN,1);Activated_Outputs_Outputlayer = cell(4000,1);
    der_Activated_Outputs_Outputlayer = cell(4000,1);
    Activated_Outputs_Hiddenlayer = cell(4000,1);
    der_Activated_Outputs_Hiddenlayer = cell(4000,1);
    delta_Outputlayer = cell(4000,1);
    delta_Hiddenlayer = cell(4000,1);
%4000个输入进入隐藏层

%所有输入的平均激活和误差的计算
     for inp=1:1:4000
    Hjk = train_set(inp,1:784)';
    for i=1:1:HL+1
         s=Weight_Matrices{i}*[1;Hjk];%此处[1列车组]表示输入数量，外部1表示偏差
        Hjk = arrayfun(Yj,s);
        Activated_Outputs{i}=Hjk;
        der_Activated_Outputs{i} = (1-Hjk).*Hjk;
     end
..................................................................................
    end
    Average_Activation_Calculated = (Total_Activation)./4000;
    
    %Kullback-leibler散度的术语定义如下
    A1 = (Average_Activation_req)./(Average_Activation_Calculated);
    B1 = (1-Average_Activation_req)./(1-Average_Activation_Calculated);
    %这些值在一个时期内保持不变，并在每个新时期发生变化
    
    %计算误差。必须添加稀疏性和权重衰减项
    if rem(epoch,10)==0 || epoch ==1
    J_mat(end+1)= sum(J_epoch);
    end
    %使用适当的公式添加错误项。这里有测试版术语，而
    %加法以及所有权重参数都必须被平方并相加。添加
    accum_del_Weights_Outputlayer = zeros(784,151);
    del_Weights_Outputlayer = zeros(784,151);
    for inp=1:1:4000
    %计算增量值
    delta_Outputs = [train_set(inp,1:784)'-Activated_Outputs_Outputlayer{inp}].*der_Activated_Outputs_Outputlayer{inp};
    delta_Outputlayer{inp} = delta_Outputs;
    del_Weights_Outputlayer = (ita_1.*(delta_Outputs))*[1; Activated_Outputs_Hiddenlayer{inp}]' + (alpha.*del_Weights_Outputlayer);
    accum_del_Weights_Outputlayer = accum_del_Weights_Outputlayer + del_Weights_Outputlayer;
    end
    %Wij更改在此处完成1个输入
    accum_del_Weights_Hiddenlayer = zeros(150,785);
    del_Weights_Hiddenlayer = zeros(150,785);
    for inp = 1:1:4000
    delta_Inputs = ((Weight_Matrices{2,1}(:,2:TN(2)+1)'*(delta_Outputlayer{inp})) - beta*(B1-A1)).*(der_Activated_Outputs_Hiddenlayer{inp});
    delta_Hiddenlayer{inp} = delta_Inputs; 
    del_Weights_Hiddenlayer = [ita_1.*(delta_Inputs)]*[1 train_set(inp,1:784)] + [alpha.*(del_Weights_Hiddenlayer)];
    accum_del_Weights_Hiddenlayer = accum_del_Weights_Hiddenlayer + del_Weights_Hiddenlayer;
    end
    %计算的累计权重。
    Weight_Matrices{1,1} = Weight_Matrices{1,1} + (accum_del_Weights_Hiddenlayer)./4000 - 4000*decay_constant*[zeros(150,1) Weight_Matrices{1,1}(:,2:TN(1)+1)];
    Weight_Matrices{2,1} = Weight_Matrices{2,1} + (accum_del_Weights_Outputlayer)./4000 - 4000*decay_constant*[zeros(784,1) Weight_Matrices{2,1}(:,2:TN(2)+1)];
end
........................................................................................
up3041