文章目录


本篇博客是我在学习完九种背包问题后的总结，文中可能有我对背包问题理解不当的地方，或是描述不清楚的地方，希望大家能够指出。
由于水平有限 蒟蒻求理解，本篇文章将持续更新，如果发现有更通俗易懂的讲法，我也会添加上，九种背包对应的练习题我以后遇到之后也会添加进博客里。
本篇文章持续更新中…

其实九种背包问题都是由01背包问题延伸而来，因为其他背包问题都是在01背包问题上加了一些其他条件或限制。只要01背包的思想完全掌握，那么在学习其他背包问题的时候都能够很快理解，在解决其他背包问题时基本只是在01背包基础上，增加一些判断，或是在01背包思想的基础上根据题目要求做出一些调整。因此本篇在刚开始介绍01背包的时候会花费较多笔墨，尽量保证大家能够理解01背包，接下来后面的背包问题就会只对于题目相对01背包作出的更改进行讲解。

一、01背包

问题描述及要求

给定 n n n个物品，以及一个容量大小为 m m m的背包，然后给出 n n n个物品的体积及价值，求背包最大价值是多少，也就是选择总体积不超过 m m m的物品，然后使总价值最大。

适用范围

01背包适用于求解有约束条件的贪心选择问题，就像题目描述的情况，并且要求每个物品只能选一次。

思路分析

动态规划思想就是将一个问题分解为若干子问题，并由子问题逐步得到最终答案。因此将上述问题分解为若干子问题非常重要。

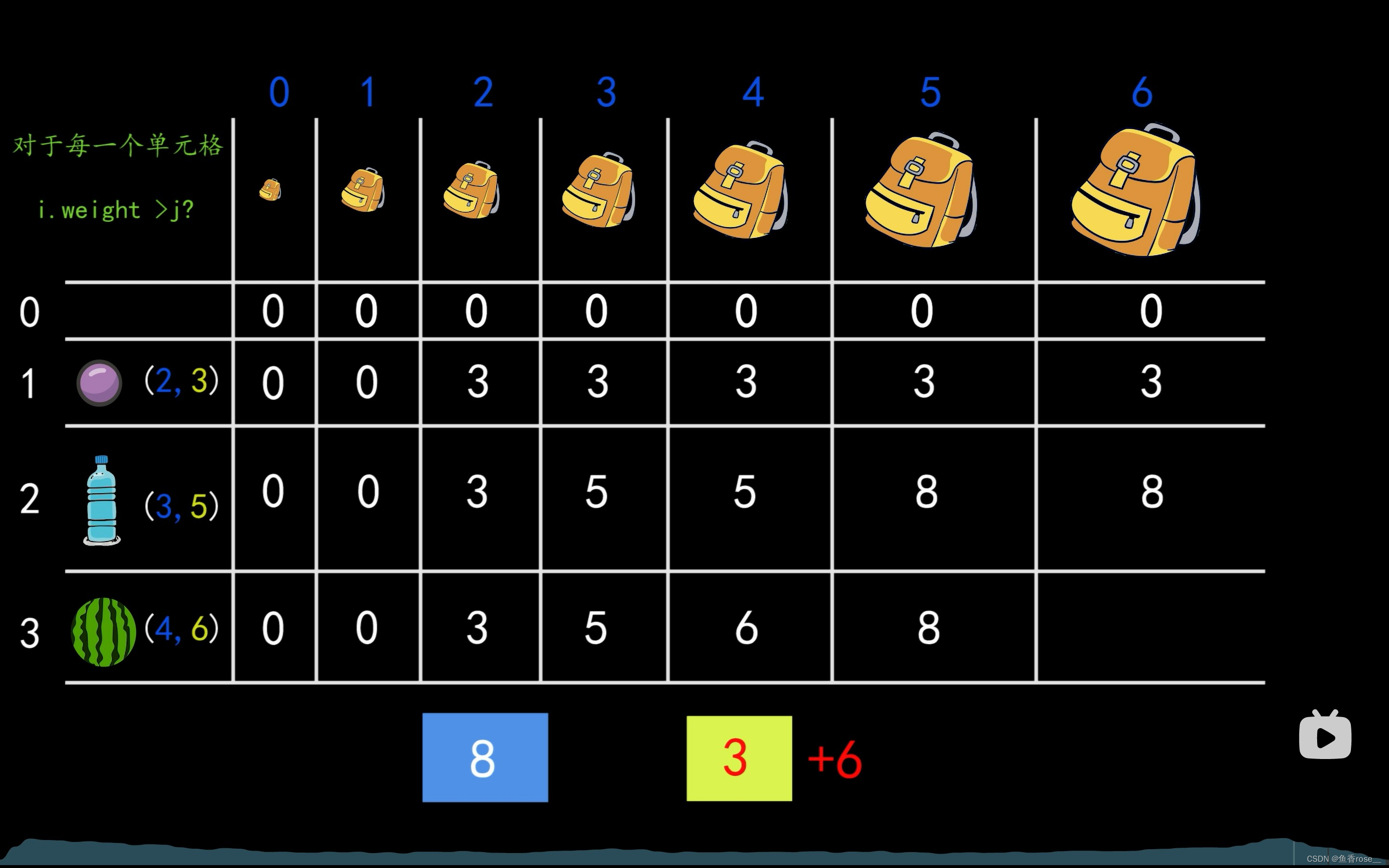
题目要求在容量大小为m的情况下选n个物品，那么我们是否可以将问题分解为在容量大小为0~~m的情况下选择n个物品的子问题。其次再进一步，在求容量0~m时，我们将问题分解为选择编号从1到n的物品。此时我们成功将问题转化为二维，而求解过程中的状态我们可以使用一个二维数组 f [ i ] [ j ] f[i][j] f[i][j]来记录不同子问题的结果。

在这里插入图片描述
注：这是我们当时学习动态规划时看的图片，但是这个视频找了好久都没找到，实在没办法@原作者。

动态规划中最重要的就是状态转移方程，其实就是由子问题的状态向总问题转移的过程。

f [ i ] [ j ] = m a x ( f [ i ] [ j ] , f [ i − 1 ] [ j − v [ i ] ] + w [ i ] ) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]) f[i][j]=max(f[i][j],f[i−1][j−v[i]]+w[i])

解释一下这个状态转移方程，其中 f [ i ] [ j ] f[i][j] f[i][j]表示的选择前 i i i个物品在背包容量为 j j j的情况下的最大价值， w [ i ] w[i] w[i]和 v [ i ] v[i] v[i]分别表示第 i i i个物品的价值和体积。 然后我们从1到 n n n个物品开始枚举，第二层循环枚举容积为0到 m m m。然后我们每次选 i i i个物品时，此时先不考虑最大容量，这个时候的 f [ i ] [ j ] f[i][j] f[i][j]状态是怎么得到的呢？

其实很好分析，当前状态是由选择 i − 1 i-1 i−1的状态得来的， i − 1 i-1 i−1表示的是选择前 i − 1 i-1 i−1个物品，不包括第 i i i个，因此这时在看状态转移方程就会发现，当前状态就是由其前一个状态转移而来，具体转移规则就是判断哪个的价值最大，是 f [ i ] [ j ] f[i][j] f[i][j]（也就是本身）还是 f [ i − 1 ] [ j − v [ i ] ] + w [ i ] f[i-1][j-v[i]]+w[i] f[i−1][j−v[i]]+w[i]（选择前 i − 1 i-1 i−1个物品的最优解的减去当前物品的体积再加上当前物品的价值）表示的就是选择当前新增的这个物品，但是如果选择的话，需要保证容量足够，因此上一个状态就变为了选择前 i − 1 i-1 i−1个物品，且容积为 j − v [ i ] j-v[i] j−v[i]。

上面这段话一定要结合这段代码来理解

//数组a为体积，b为价值，dp记录子问题状态
for(int i = 1; i <= n; i ++ ) {
		for(int j = 0; j <= m; j ++ ) {
			dp[i][j] = dp[i - 1][j];
			//肯定不能少了判断j是否大于a[i]的情况，因为此时如果枚举的j小于当前的a[i]那么当前子背包是装不了这个物品的
			if(j >= a[i]) dp[i][j] = max(dp[i][j], dp[i - 1][j - a[i]] + b[i]);
		}
	}

优化

理解完前面的思想之后我们就可以进行优化了，其实背包问题的优化过程和问题本身联系不大，主要是对代码逻辑进行优化，问题的整体思路不变。

我们先尝试将二维数组的第一维直接去掉，务必敲一下代码，然后自己在编译器上试一下，只看不练是非常低效的学习方式
然后就编译错误了。
然后我们要考虑，如何在改为一维的情况下使这串代码的功能和二维一样。在二维中我们每次由 d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i - 1][j] dp[i][j]=dp[i−1][j]来做状态转移，而且我们会发现 d p [ i ] [ j ] dp[i][j] dp[i][j]只与 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]有关（其实通过这个规律就可以将其做滚动数组优化）。为什么当前状态要由前一个状态得到？这是因为我们要保证每个物品只选一次，而枚举1到n个物品并让每个状态由其前一个状态得到这种思路就是防止一个物品选多次。我们要保证一维状态的 d p [ j − v [ i ] ] dp[j-v[i]] dp[j−v[i]]表示的是二维状态下的 d p [ i − 1 ] [ j − v [ i ] ] dp[i-1][j-v[i]] dp[i−1][j−v[i]]才行。容量从后往前枚举的话就不会出现当前物品影响下一个容量，而这种影响就相当于一个物品被选了多次。

一维优化的01背包在后面学习的其他背包中都能用到，因此必须理解下面一维优化的代码当然可以背下来

C++实现代码（一维数组优化）

#include<bits/stdc++.h>

using namespace std;

const int N = 1010;

int n, m, a[N], b[N], f[N];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ) cin >> a[i] >> b[i];
    
    for(int i = 1; i <= n; i ++ ) {
    	//01背包，一个物品最多只能选一次，在遍历到一个物品时，对体积进行枚举，但是不能让同一个物品  \
		  对dp数组修改多次，所以可以从m到0枚举体积 
        for(int j = m; j >= a[i]; j -- ) {
            f[j] = max(f[j], f[j - a[i]] + b[i]);
        }
    }
    
    cout << f[m] << endl;
    
    return 0;
}

二、完全背包

问题描述及要求

给定 n n n种物品，以及一个容量大小为 m m m的背包，然后给出 n n n个物品的体积及价值，求背包最大价值是多少，也就是选择总体积不超过 m m m的物品，然后使总价值最大。

适用范围

完全背包和01背包唯一的不同我用粗体标注出来了，对，就是“个”变为了“种”，这也就意味着每个物品我们可以选多次，没有限制。

思路分析

完全背包表示每个物品可以任意选，在01背包二维思路的基础上，我们在枚举的时候需要在多一层循环用来枚举当前物品的个数。看一下未优化版的代码：

for(int i = 1; i <= n; i ++ ) {
		for(int j = 0; j <= m; j ++ ) {
			dp[i][j] = dp[i - 1][j];
			for(int k = 1; k * a[i] <= j; k ++ ) {
				dp[i][j] = max(dp[i][j], dp[i - 1][j - k * a[i]] + k * b[i]);
			}
		}
	}

还记得01背包的思想吗，当然我说的是1维优化过的01背包，在01背包一维优化问题中，我们为了保证每个物品最多只取一次，因此我们枚举容量时从后往前枚举，这样保证了一个物品不会影响状态多次，即符合了每个物品只选一次。但是在完全背包问题中，题目要求的就是每个物品可以任意选多次。那么我们直接从0开始枚举容量即可。

C++实现代码

//一维数组优化
#include<bits/stdc++.h>

using namespace std;

const int N = 1010;

int n, m, a[N], b[N], dp[N];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n;  i++ ) cin >> a[i] >> b[i];
    
    for(int i = 1; i <= n; i ++ ) {
    	//在完全背包问题中，每个物品能选择多次，因此每个物品可以对dp数组修改多次	\
		  这时就可以从0到m枚举体积，当前物品对体积的修改可以影响接下来的体积状态 
        for(int j = a[i]; j <= m; j ++ ) {
            dp[j] = max(dp[j], dp[j - a[i]] + b[i]);
        }
    }
    
    cout << dp[m] << endl;
    
    return 0;
}

三、多重背包

问题描述及要求

给定 n n n种物品，以及一个容量大小为 m m m的背包，然后给出 n n n个物品的体积、价值及个数，求背包最大价值是多少，也就是选择总体积不超过 m m m的物品，然后使总价值最大。

适用范围

看问题描述中粗体部分，这次每个物品可能不止一个，也不全都是多个，而是有给定的数量。往下看看是怎么解决的吧！

思路分析

既然每个物品不止一个，那我们是否可以将不止一个的物品分开，将两个一样的物品合在一起看作是一个，对！想到这个思路就非常的nice！这样我们就可以将多重背包转换为一个01背包来解答，只是原本给定的 n n n个物品变多了，那具体变成了多少个呢？其实不需要来具体计算，我们可以用vector数组存所有物品即可。

想到了上面的思路，就感觉非常的简单了，但是仔细思考一下，这样原本的n种物品也将增加很多，而01背包是二重循环，当n很大的时候会超时，那么我们该如何分才能1、保证将x个物品分的份数最少，2、保证任意几份能组成小于x的数字，3、每份相加和为x。
思考一下上面三个要求，是不是觉得非常熟悉。对！我们想到了二进制！众所周知任何数字都能用二进制表达，因此我们用倍增的思想（其实就是二进制）将x个物品进行划分，这样就能解决前两点，然后将余下的个数当作一组这样就解决了第三点。
话不多说上代码

C++实现代码（无优化，纯暴力）

#include<bits/stdc++.h>

using namespace std;

const int N = 1e3 + 10;

int n, m;
int a[N], b[N], c[N];
int dp[N];

int main(void) {
	
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ ) {
		cin >> a[i] >> b[i] >> c[i];
	}
	
	for(int i = 1; i <= n; i ++ ) {
		for(int j = m; j >= a[i]; j -- ) {
			for(int k = 1; k <= c[i] && k * a[i] <= j; k ++ ) {
				dp[j] = max(dp[j], dp[j - k * a[i]] + k * b[i]);
			}
		}
	}

	cout << dp[m] << endl;

	return 0;
}

C++实现代码（二进制优化）

//多重背包问题——二进制优化
#include<bits/stdc++.h>

using namespace std;

const int N = 1e4 + 10;

vector<pair<int, int>> v;
int n, m ,dp[N]; 

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ) {
        int a, b, c; cin >> a >> b >> c;
        for(int j = 1; j <= c; j *= 2 ) {
            c -= j;
            v.push_back({a * j, b * j});
        }
        if(c > 0) v.push_back({a * c, b * c});
    }
    for(auto i : v) {
        for(int j = m; j >= i.first; j -- ) {
            dp[j] = max(dp[j], dp[j - i.first] + i.second);
        }
    }
    
    cout << dp[m] << endl;
    
    return 0;
}

C++实现代码（单调队列优化）

如果数据范围太大的情况下，二进制优化也无法解决问题，这时候我们就需要考虑进一步优化。
具体做法是使用单调队列进行优化，具体都已在代码中注释讲解

//多重背包问题——单调队列优化
#include<bits/stdc++.h>

using namespace std;

#define IOS ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
#define ll long long
#define ull unsigned long long
#define endl '\n'
#define fi first
#define se second

typedef pair<int, int> pir;
const int mod = 1e9 + 10;
const int N = 1e5 + 10;

int n, m;
int dp[N], g[N], q[N];

int main(void) {
	IOS
	
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ ) {
		int a, b, c; cin >> a >> b >> c;
		memcpy(g, dp, sizeof dp);
		
		//遍历余数 
		for(int j = 0; j < a; j ++ ) {	
			int h = 0, t = -1;
			
			//遍历余数为j这一类的体积
			for(int k = j; k <= m; k += a) {	
				//当前层的dp[k] 暂时等于上一层的g[k] 相当于dp[i][j] = dp[i - 1][j]
				dp[k] = g[k];
				
				//这里一共有c + 1个元素，c = 0也算一个， 所以这里不是k - c * a + 1 
				//队列存的是下标，也是体积 
				if(h <= t && k - c * a > q[h]) h ++ ;
				
				//队列中最大的和c = 0的进行比较 
				if(h <= t) dp[k] = max(dp[k], g[q[h]] + (k - q[h]) / a * b);
				
				//q[t]这个体积下的价值，再加上与k体积相差的体积数的价值，才能与g[k]进行比较 
				while(h <= t && g[q[t]] - (q[t] - j) / a * b <= g[k] - (k - j) / a * b) t -- ;
				q[++ t] = k;
			}
		}
	}

	cout << dp[m] << endl;

	return 0;
}

四、混合背包

问题描述及要求

给定 n n n种物品，以及一个容量大小为 m m m的背包，然后给出 n n n个物品的体积、价值，求背包最大价值是多少，也就是选择总体积不超过 m m m的物品，然后使总价值最大。
**区别：**本题的物品共有三种，1、该物品只有一个；2、该物品有无限多个；3、该物品有x个

适用范围

这道题好熟悉，感觉像是把上面的几种情况全部混合在一起了，同时有01背包、完全背包、多重背包。

思路分析

这道题其实也就看着复杂，其实就是把三种背包问题放一起了。我们来分析一下，上面讲多重背包的时候，通过二进制优化，将多重背包分解为01背包来写，那么现在就变成了两种背包问题混合了，那么怎么处理呢？
01背包和完全背包有什么区别？？？
一维优化状态下，好像也就只有背包容量枚举的顺序不一样，枚举背包容量在第二层循环，那么我们直接在第一次循环里判断一下，如果当前物品只能选一次，那么就按照01背包性质从后往前枚举背包容量，完全背包则从前往后枚举容量即可。

C++实现代码

#include<bits/stdc++.h>

using namespace std;

const int N = 1e4 + 10;

int n, m, dp[N];
struct node {
	int kind, a, b;
}; 
vector<node> v;

int main() {
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ ) {
		int x, y, z; cin >> x >> y >> z;
		if(z == -1) v.push_back({1, x, y});			//01
		else if(z == 0) v.push_back({0, x, y});		//完全 
		else {
			for(int j = 1; j <= z; j *= 2) {		//01 
				z -= j;
				v.push_back({1, x * j, y * j});
			}
			if(z) v.push_back({1, x * z, y * z});
		}
	}
	for(auto i : v) {
		if(i.kind) { 	//01
			for(int j = m; j >= i.a; j -- ) 
				dp[j] = max(dp[j], dp[j - i.a] + i.b);
		}  else {			//完全 
			for(int j = i.a; j <= m; j ++ )
				dp[j] = max(dp[j], dp[j - i.a] + i.b);
		}
	}
	
	cout << dp[m] << endl;
	
	return 0;
}

五、二维费用的背包问题

问题描述及要求

给定 n n n个物品，以及一个容量大小为 m m m、能承受质量为 W W W的背包，然后给出 n n n个物品的体积、价值及质量，求背包最大价值是多少，也就是选择总体积不超过 m m m的物品，然后使总价值最大。

适用范围

这个题目描述我是粘贴01背包的问题描述，其实上面的问题描述都是。但是与01背包的不同我都直接用粗体显示了。所以它与01背包是很相似的，只是限制条件增加了一个。适用于两个条件约束的01背包。

思路分析

这道题在01背包的基础上多了一个限制，怎么处理？？？
无所谓，我会加一层循环
解决方式确实是加一层枚举，即遍历每一个物品时枚举容量和质量。

C++实现代码

#include<bits/stdc++.h>

using namespace std;

const int N = 1010;

int n, m, v;
int dp[N][N];

int main() {
    cin >> n >> v >> m;
    for(int i = 1; i <= n; i ++ ) {
        int a, b, c; cin >> a >> b >> c;
        for(int j = v; j >= a; j -- ) {
            for(int k = m; k >= b; k -- ) {
                dp[j][k] = max(dp[j][k], dp[j - a][k - b] + c);
            }
        }
    }
    
    cout << dp[v][m] << endl;
    
    return 0;
}

六、分组背包

问题描述及要求

给定 n n n个物品，以及一个容量大小为 m m m的背包，然后给出 n n n个物品的体积及价值，n个物品是分为若干组，每组最多只能选择一个物品。求背包最大价值是多少，也就是选择总体积不超过 m m m的物品，然后使总价值最大。

适用范围

这道题在01背包的基础上，加了一个条件，即背包分为若干组，每组最多只能选一个物品。

思路分析

每组最多只能选一个物品圈起来，要考的！
每次读入一组物品，怎么能保证每组物品最多只选一个

多重背包问题是分组背包的一种特殊情况，为什么这么说？在多重背包中，每种物品有多个，可以看作我们将每种物品分别将1个、2个、3个、、、x个打包放在一组，然后每次在这组种选一个，因此是一种特殊的分组背包，所以多重背包问题我们才能用二进制或是单调队列进行优化，将其时间复杂度降得很低。

但是在分组背包中，我们只能枚举每组的决策，相当于再加上一层循环。

看到我们代码中给的两个样例了吗？
将样例下面的循环注释去掉，用两组样例跑一边，结合结果去理解很快的！！！
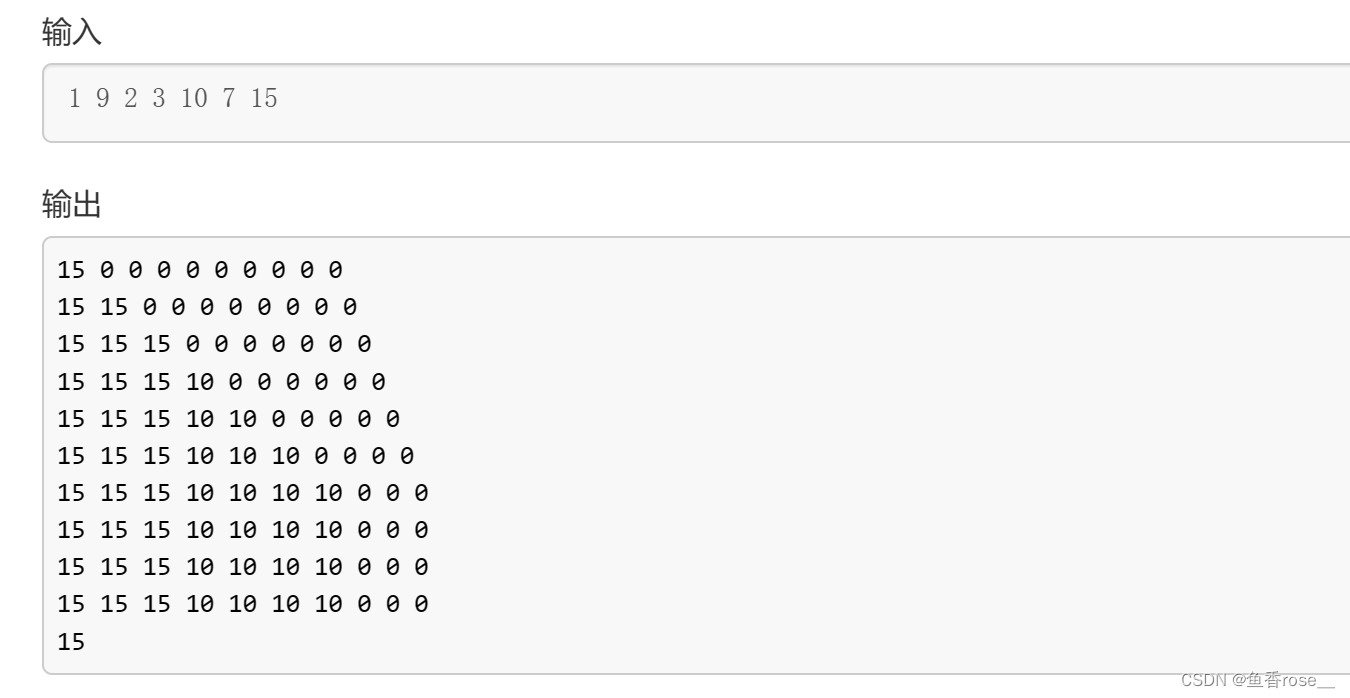
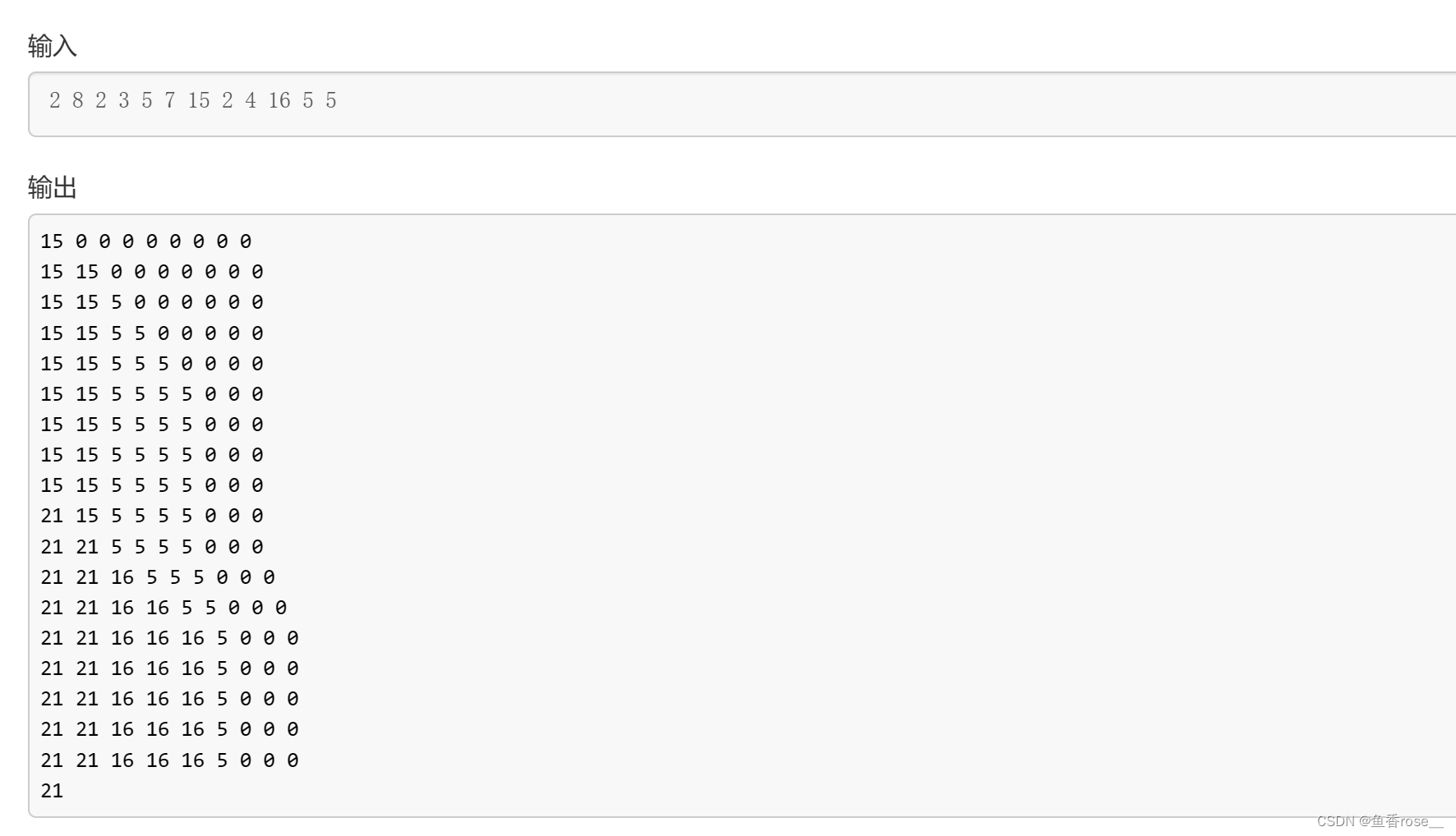
在这里插入图片描述
在这里插入图片描述

C++实现代码

#include<bits/stdc++.h>

using namespace std;

const int N = 1e4 + 10;

int n, m, dp[N], a[N], b[N];

int main() {
	
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ ) {
		int s; cin >> s;
		for(int j = 1; j <= s; j ++ ) cin >> a[j] >> b[j];
		
		for(int j = m; j >= 0; j -- ) {
			for(int k = 1; k <= s; k ++ ) {
			    //同一组里边出现叠加才代表选了多个，但是每次枚举容量j时是从m到0枚举，不会影响后面的状态 \
			      不会导致元素叠加，达到每组只选一个物品的目的
			    //当前组其他物品（未被选中）对dp数组做出的修改会影响接下来的其他组，但是这些影响代表    \
			      选择当前组的不同状态，不会出现超过两个修改同时对接下来其他组产生影响的情况            \
			      （所说的这种情况相当于前在同一个组里选了两个物品）
				if(j >= a[k]) dp[j] = max(dp[j], dp[j - a[k]] + b[k]);
			}
//			来组样例1：1 9 2 3 10 7 15 
//              样例2：2 8 2 3 5 7 15 2 4 16 5 5
//	        for(int ii = m; ii >= 0; ii -- ) cout << dp[ii] << " ";
//            	cout << endl;
		}
	}
	
	cout << dp[m] << endl;
	
	return 0;
}

七、有依赖的背包问题

问题描述及要求

有 N N N个物品和一个容量是 V V V的背包。物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。
给出物品的体积、价值和依赖的物品编号，并保证所有物品组成一棵树，依赖的物品编号为-1则表示为根节点。
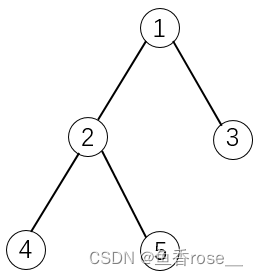
在这里插入图片描述
注：图片来自https://www.acwing.com/problem/content/10/

适用范围

这种类型的背包问题主要是一个依赖关系，即选择子节点就必须选择父节点。是捆绑在一起的。

有依赖的背包问题是将树和 d p dp dp结合在一起，但是可以选择建树或者不建树来写（具体思路都一样），我最后会将两种方式都写在下边。

思路分析

有依赖关系的背包问题，他的每一个物品的选择情况都有其子节点的选择情况构成，而子节点的选择情况又由父节点决定（父节点如果不选，则所有子节点都选不了）。我们将每个父节点及其子节点看作是一个分组，父节点的情况由子节点所有选择情况中的一种构成，然后我们就成功的将该问题转化为了一道分组背包问题。

上面的思路如何来理解呢？？？
我们定义 f [ i ] [ j ] f[i][j] f[i][j]数组， i i i表示节点， j j j表示所占容量，那么 f [ i ] [ j ] f[i][j] f[i][j]就表示 i i i节点在 j j j容量的情况下的最大价值。现在能和分组背包联系起来了吗？感觉没有关联也没问题，再接着往下看。在分组背包问题中，我们的第三维枚举决策的时候是枚举当前组里的物品，并且只能选一个物品。

而在此问题中，我们将每棵子树看作一个分组，将父节点的所有子节点的状态看作是组内的物品，枚举子节点所有选择情况所占体积，因为不同体积代表子节点的不同选择状态。然后我们从根节点开始递归到叶子节点，然后从叶子节点开始选择，每个节点的选择情况枚举完之后再返回到其父节点继续选择，最终返回到根节点进行选择。最后 f [ r o o t ] [ m ] f[root][m] f[root][m]即为以root为根节点的树在容量为m情况下的最大价值。但需要注意，此时代表的时容量小于等于m的最大价值，同基础01背包一样，不是代表容量刚好为m时的最大价值。

单纯纸上谈兵效率太低，我把主要思路以及每一步的思路作为注释写入代码中。

C++实现代码（vector存子节点）

#include<bits/stdc++.h> 

using namespace std;

const int N = 110;

int n, m, root;
//dp[x][y]表示选择以x为根节点的物品，在容量不超过y时所获得的最大价值 
int dp[N][N];
int a[N], b[N];
//用vector数组存每个父节点的儿子 
vector<int> v[N];

void dfs(int x) {
	//初始化dp[x][a[x] ~ m] = b[x] 
	for(int i = a[x]; i <= m; i ++ ) dp[x][i] = b[x];
	//遍历当前节点的所有儿子 
	for(int i = 0; i < v[x].size(); i ++ ) {
		int y = v[x][i];
		dfs(y);
		//每个物品只能选一次，所以从大到小枚举容量
		//每次计算节点时都是：先遍历所有子节点（物品） -> 枚举容量 -> 枚举决策（子节点的状态） 
		for(int j = m; j >= a[x]; j -- ) {
			//分给子树y的空间不能大于 j - v[x]，不然无法选根节点物品x 
			//k为分给子节点的容量 
			for(int k = 0; k <= j - a[x]; k ++ ) {
				dp[x][j] = max(dp[x][j], dp[x][j - k] + dp[y][k]);
			}
		}
	}
}

int main() {
	
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ ) {
		int fa; cin >> a[i] >> b[i] >> fa;
		if(fa == -1) root = i;
		else v[fa].push_back(i);
	}
	//从根节点开始递归 
	dfs(root);
	
	cout << dp[root][m];
	
	return 0;
}

C++实现代码（邻接表建树）

//邻接表建树求解 
//有依赖的背包问题是指物品之间存在依赖关系，这种依赖关系可以用一棵树来表示，要是我们想要选择子节点就必须连同其父节点一块选。\
我们可以把有依赖的背包问题看成是分组背包问题，每一个结点是看成是分组背包问题中的一个组，子节点的每一种选择我们都看作是组	\
内的一种物品，因此我们可以通过分组背包的思想去写。但它的难点在于如何去遍历子节点的每一种选择，即组内的物品，				\
我们的做法是从叶子结点开始往根节点做，并使用数组表示的邻接表来存贮每个结点的父子关系。
#if 0
#include<bits/stdc++.h>

using namespace std;

const int N = 110;

int n, m, root;
int h[N], e[N], ne[N], idx;
//h数组是邻接表的头它的下表是当前节点的标号，值是当前结点第一条边的编号（其实是最后加入的那一条边），e数组是边的集合，		\
它的下标是当前边的编号，数值是当前边的终点；ne是nextedge，如果ne是-1表示当前结点没有下一条边，ne的下标是当前边的编号，		\
数值是当前结点的下一条边的编号，idx用于保存每一条边的上一条边的编号。														\
这样我们就知道了当前结点的第一条边是几，这个边的终点是那个结点，该节点的下一条边编号是几，那么邻接表就完成了

//f[N][N]第一维表示物品，第二维表示容积 
int v[N], w[N], f[N][N];

void add(int a, int b) {
    //该方法同于向有向图中加入一条边，这条边的起点是a，终点是b，加入的这条边编号为idx 
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u) {
    //对当前结点的边进行遍历 
    for(int i = h[u]; i != -1; i = ne[i]) {
        //e数组的值是当前边的终点，即儿子结点
        int son = e[i];
        dfs(son);
        //遍历背包的容积，因为我们是要遍历其子节点，所以当前节点我们是默认选择的。                  \
          这个时候当前结点我们看成是分组背包中的一个组，子节点的每一种选择我们都看作是组内一种物品，\
          所以是从大到小遍历。我们每一次都默认选择当前结点，因为到最后根节点是必选的。 
        for(int j = m - v[u]; j >= 0; j -- ) {
            //去遍历子节点的组合 
            for(int k = 0; k <= j; k ++ ) {
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
            }
        }
    }
    //加上刚刚默认选择的父节点价值
    for(int i = m; i >= v[u]; i -- ) {
        f[u][i] = f[u][i - v[u]] + w[u];
    }
    //因为我们是从叶子结点开始往上做，所以如果背包容积不如当前物品的体积大，\
      那就不能选择当前结点及其子节点，因此赋值为零 
    for(int i = 0; i < v[u]; i ++ ) f[u][i] = 0;
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ) {
        int p; cin >> v[i] >> w[i] >> p;
        if(p == -1) root = i;
        //如果不是根节点就加入邻接表,其中p是该节点的父节点，i是当前是第几个节点
        else add(p, i);
    }
    dfs(root);
    
    cout << f[root][m] << endl;
    
    return 0;
}

八、背包问题求方案数

问题描述及要求

给定 n n n个物品，以及一个容量大小为 m m m的背包，然后给出 n n n个物品的体积及价值，求背包最大价值是多少，也就是选择总体积不超过 m m m的物品，然后使总价值最大。然后输出最优解的方案数。

适用范围

题目要求输出最优解方案数

思路分析

这就是一个01背包的题，不过要求变了，要求输出最优解的方案数。因此重新思考一下01背包的思想。
我们发现，01背包的状态表示为小于等于 j j j的情况下最优解，那我们就需要将状态变为等于 j j j情况下的最优解。然后我们需要再开一个数组记录方案数，表示为体积为i的情况下方案数是多少。
要实现体积恰好为 j j j的情况下最优解为多少，如何实现呢？只需将 f f f数组初始化时除了0，其他位置全部初始话为大的负数即可。思考一下为什么是这样，可以输出一下所有的 f f f观察一下。

C++实现代码

#include<bits/stdc++.h>

using namespace std;

const int N = 1010;
const int mod = 1e9 + 7;
const int INF = 1e7 + 10; 

int n, m, f[N], g[N];

int main() {
	 
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ ) f[i] = -INF;
	g[0] = 1;
	int res = 0;
	for(int i = 1; i <= n; i ++ ) {
		int a, b; cin >> a >> b;
		for(int j = m; j >= a; j -- ) {
			int t = max(f[j], f[j - a] + b);
			int s = 0; 
			if(t == f[j]) s += g[j];
			if(t == f[j - a] + b) s += g[j - a];
			s %= mod;
			f[j] = t; g[j] = s;
		}
	}
	int mx = 0;
	for(int i = 1; i <= m; i ++ ) mx = max(mx, f[i]);
	
	for(int i = 1; i <= m; i ++ ) {
		if(f[i] == mx) res += g[i];
	}
	
	cout << res << endl;
	
	return 0;
}

背包问题求具体方案

问题描述及要求

给定 n n n个物品，以及一个容量大小为 m m m的背包，然后给出 n n n个物品的体积及价值，求背包最大价值是多少，也就是选择总体积不超过 m m m的物品，然后使总价值最大。然后输出最优解的方案，并输出字典序最小的最优方案。

适用范围

要求输出具体最优方案。

思路分析

在01背包的基础上要求输出最优方案，且字典序最小，按照01背包朴素二维的思路其实很好求，只需输出时用循环，判断当前最优解是由上一步那个状态得到的。
还记得01背包状态转移方程吗？

f [ i ] [ j ] = m a x ( f [ i ] [ j ] , f [ i + 1 ] [ j − v [ i ] ] + w [ i ] ) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]) f[i][j]=max(f[i][j],f[i+1][j−v[i]]+w[i])

只需在逆着求上一步的状态即可。
同时本题要求输出字典序最小的最优解，那么我们在求解的时候从n开始枚举每一个背包即可。
从最后一个物品开始向前枚举，会出现前面的物品后考虑，也就是影响状态的顺序靠后，最后枚举求方案数时是判断的最晚影响状态的物品，物品从后往前枚举，则最后影响状态的也就是最前面的物品。

C++实现代码

#include<bits/stdc++.h>

using namespace std;

const int N = 1010;

int n, m, f[N][N], v[N], w[N];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    
    //从最后一个物品开始向前枚举，会出现前面的物品后考虑，也就是影响状态的顺序靠后，\
      最后枚举求方案数时是判断的最晚影响状态的物品，物品从后往前枚举，则最后影响状态的也就是最前面的物品
    for(int i = n; i >= 1; i -- ) {
        for(int j = 0; j <= m; j ++ ) {
            f[i][j] = f[i + 1][j];
            if(j >= v[i])
                f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }
    }
    
    int val = m;
    for(int i = 1; i <= n; i ++ ) {
        if(val >= v[i] && f[i][val] == f[i + 1][val - v[i]] + w[i]) {
            cout << i << " ";
            val -= v[i];
        }
    }
    
    return 0;
}
# 算法 # 动态规划 # c++
Logo
AtomGit 开源协作平台测评赛

瓜分20万奖金 获得内推名额 丰厚实物奖励 易参与易上手

更多推荐

mac 使用brew卸载安装node

mac 使用brew卸载安装node卸载1. 查看当前安装的node版本：node -v2. 卸载node：brew uninstall node@版本号 --force比如安装的是12.18.1，使用brew uninstall node@12 --force。还有另外两种现在不能用的方法：使用brew uninstall node，会报错：Error: No such keg: /usr/lo

avatar 开放原子开发者工作坊
cover

训练集、验证集、测试集（附：分割方法+交叉验证）

avatar 开放原子开发者工作坊
cover

2024校源行“就业技能培训系列专题课”正式启动

avatar 开放原子开发者工作坊