在平常的搜索算法中，BFS和DFS算是盲目搜索，BFS搜索从a到b的最短路径，会从自己各个方向依次扩展，效率低下，因此出现了启发式搜索，A算法和A*算法。

对于A算法，他是使用了一个评价函数f(n)=g(n)+h(n)，g(n)表示从起点到当前点的代价，h(n)表示预估代价，就是从当前点到终点的代价，每次选取当前f(n)最小的进行扩展。

A*算法则是对A算法进行了优化，让h(n)≤h *(n)，对h(n)进行了限制，是优化版的A算法。

---

A*算法

• 在模型的状态空间很大时，如果用传统BFS找最小步数，会导致MLE或者TLE，因此可以使用A*算法

• A*算法就是启发式搜索，考虑当前已有代价和到终点的预估代价，因此可以优先扩展整体代价最小的点，可以少扩展许多无用的点

A*算法基本步骤:

1. 用一个优先队列来存(小根堆),将起点入队，队列中存储的是d(u)+f(u) 和 当前状态, d(u)是从起点到u的实际距离,f(u)是从u到终点的估价距离

2. 每次从队头取出元素进行扩展，将扩展到的元素入队

3. 直到终点出队才能求出最小值

A*算法注意事项:

• 使用A*算法的前提是该问题必须有解，如果无解，就和普通bfs一样，搜索全部空间，并且A*使用优先队列，每次入队时间复杂度为logn，比普通bfs时间复杂度还高

• A*算法当终点出队时，可以求出终点到起点的最小步数，且只能求出起点到终点的最小步数，其他点出队不一定是最小步数

• A*算法必须满足f(u) <= g(u)，f(u)是从u到终点的预估代价，g(u)是从u到终点的实际代价

---

证明: 为什么终点出队时，为最优解

设终点出队时的距离为d，假设不是最优解，则 d > d0(最优解)
当前队列中一定存在一个点u是在最优路径上的【最差是起点】,那么d(u) + f(u) <= d(u) + g(u) = d0，那么d > d0 > d(u) + f(u)，
即当前出队的应该是u这个点，矛盾，因此终点出队一定是最优解

---

证明: 为什么其他点出队不一定为最小值:

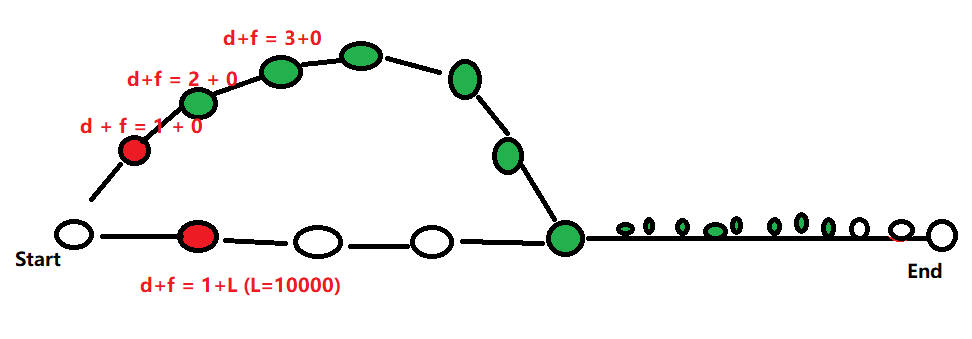
如图所示，设每条边权值为1，首先起点扩展出两个红色的点，设上边点的估价值都为0，下边点的估价值为一个很大的数，那么就会一直去扩展上边的点，当两条边交点处那个绿色的点出队后，他的距离是用上边那条边计算得到的，不是最小值，他出队后对继续向后扩展，直到扩展到某个点T，或者扩展到终点，然后继续出队时，当前队列中最小值就下边红色的点，因为f(u) <= g(u)，即L的长度是小于等于他到终点的真实长度的，即当从上边的边往终点扩展时，扩展到某个点时，最差是扩展到终点时，当前的代价加上估计代价，是一定大于下边第一个红色点处的d(u) + f(u)，所以就开始从下边那条边扩展，然后就会得到最优解。将下边红色点出队，这时在依次向后扩展，一直扩展到终点，然后终点为当前队列最小值，终点出队，得到最优解